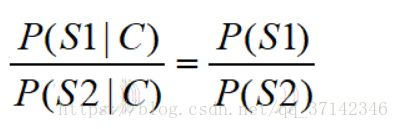【数据挖掘】NLP中文分词概述
在大数据时代,信息量越来越大,给你一篇百万文字的文章,你保证你有耐心慢慢看完吗?如果是热点新闻,我们当然会希望通过一段简洁明了的文字来概述整个文章,这时候就需要提取文章的关键字;每当我们遇到不会的问题的时候,都会想到百度,但是你有没有想过,搜索引擎是怎么样识别文本的语义进行搜索,在分析你的语义之后又是如何分析出类似的文章呈现给你,这时候就需要分析文本的相似度。NLP自然语言应用广泛,以上仅仅只是冰山一角。但是在进行NLP文本处理的时候,首先需要进行文本的分词,对于英语文本,很简单,按照空格分开即可,但是中文博大精深,语义丰富,同样的一句话可能有不同的含义,因此,中文分词也是一大难题。本篇文章主要介绍中文分词的原理,并且介绍几款简单的中文分词工具。
常见分词方法
常见的中文分词是利用字典进行匹配,最大长度查找,可以进行前向匹配,也可以进行后向匹配。前向最大长度匹配就是从头开始从词库中查找最大长度的词进行匹配。
比如有以下词库:
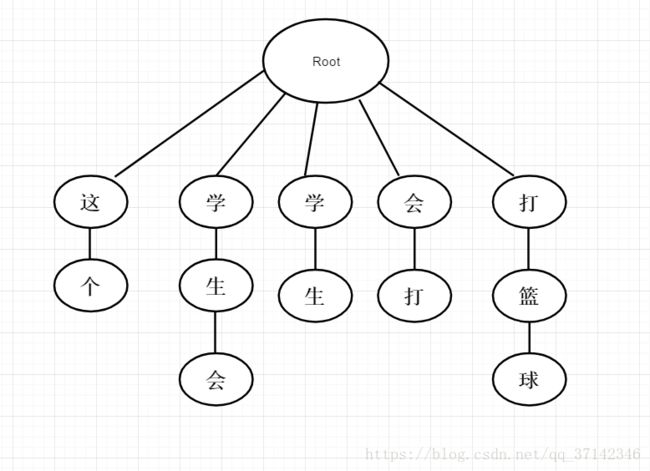
学生
学生会
会打
打篮球
这个
对以下文本进行分词:
这个学生会打篮球吗
可能会有以下两种分词方式:
这个 / 学生 / 会打 / 篮球 / 吗
这个 / 学生会/ 打篮球 / 吗
如果使用前向最大匹配,会得到下面分词语句:
这个 / 学生会/ 打篮球 / 吗
这里需要说明两个概念,在词库中的词叫做登录词,在词库外的词语叫做未登陆词。
上面“这个”,“学生会”,“打篮球”都在词库中,因此,称为登录词,“吗”不在词库中,称为未登录词。
从上面分词中我们可以看出两个问题:
- 如果文本长度过长,最大长度匹配算法的时间复杂度将会很多,因此分词时间较长
- 从分词结果上来看,并不是我们需要的语义,我们的本意是想得到“这个 / 学生 / 会 / 打篮球 / 吗”
首先,我们来探究第一个问题,为了加速分词查找词库,常使用Trie树作为数据结构来方便我们查找。
还可以使用构建DAG(有向无环图)的方式来加速匹配。
在解决了速度上的问题之后,如何正确的分词出正确的语义显得更为重要。
概率语言模型
以“南京市长江大桥”语句为例,会分词为下面两种情况:
S1:南京 / 市长 / 江大桥
S2:南京市 / 长江 / 大桥
当然,我们更希望是第二种分词方法,从概率上来讲,我们希望第二种分词方式出现的概率大于第一种。
从统计学的角度来讲,我们输入的是一个个字符串C=C1,C2,C3…Cn,对于每一个字符串会输出一个词串S=S1,S2,S3…Sm,其中,n>m。因此,对于一个特定的字符串C,都会有多个切分方案S对应,分词的任务就是在这些S中找出一个切分方案S,使得P(S|C)最大。
P(S|C)是由字符串C产生切分为S的概率,它的最大值也就是对字符串C的最大切分可能。
我们可以来求P(S|C)来判断上面两种分词方式哪个的概率大,但是直接求的话不好计算,可以计算贝叶斯公式右边的式子:
P(C|S)表达的意思是如果给定一种分词方案,可以还原出原来的句子,这个的概率是1,因为只要去掉切分符号就可以得到原来的句子;P©表达的意思是语料库中某一个句子出现的概率,比如上面在“南京市长江大桥”在语料库中出现的概率是千分之一,那么在分母上除以P©就会出现一个常数,因此,P©可以作为归一化的固定值省略掉。那么,上面的公式可以化简为:P(S|C)=P(S)
因此就将上面两种方式的概率的比较化简为S1和S2出现的概率的比较。
因此P(南京)与P(南京市)在词库中出现的概率大概是相等的,P(市长)与P(长江)出现的可能性都很大,但是P(江大桥)出现的可能性很小,也许是一个人名,P(大桥)出现的概率明显大于P(江大桥),综上所述,P(S1)大于P(S2),因此,切分方案选择S2。
上面我们将结果最终化简为使用全概率公式来表达,比如P©=P(S1)*P(S2)P(S3)…*P(Sn),当n很大的时候,有可能会出现类似于0.000000000001这么小的概率,这时候会出现内存溢出或者数组越界等情况,此时,为了防止这种情况的发生,使用单调递增函数log对数函数来表达上面的式子。
最终式子可以表示为下面的公式:
Log(P(C))=Log(P(S1))+Log(P(S2))+...+Log(P(Sn))
因此,我们可以单独来求P(S)来得出结果,按照下面公式:
P(Si)=Si在语料库中出现的次数n/语料库中的总词数N
使用对数来表达可以表示为
Log(P(Si))=Log(Freq_s)-Log(N)
上面计算P(S)的计算公式就是基于一元模型的计算公式
至于上面为什么将乘法转换为log函数之间的加法或者减法,对于计算机而言,计算log函数并不难,化简为它们之间的加法很容易得出结果,但是如果几千个数乘起来,而且是很小的小数,对计算机来说就并不那么容易,这也是以上推论的理由之一。
我们首先接着来考虑下面一个场景:
“NBA”其实就是代表着篮球,每当人们说起这个词语肯定与篮球密不可分,基本上不会有人说起“NBA”而想到“足球”这个词语,因此“NBA篮球赛”比“NBA足球赛”出现的概率大很多,其原因就是“篮球”依赖于前面的“NBA”这个词语,由此可见,有时候词语之间存在着依赖或者相互联系的关系,而我们上面认定它们之间是相互独立分布的,因此上面的假设不成立,我们不能使用全概率公式进行推导。
那么,上面的计算公式会变成这样:
P(W1,W2)=P(W1)P(W2|W1)
P(W1,W2,W3)=P(W1,W2)P(W3|W1,W2)
=>
P(W1,W2,W3)=P(W1)P(W2|W1)P(W3|W1,W2)
=>
一般形式:P(S)=P(W1,W2,W3...Wn)=P(W1)P(W2|W1)P(W3|W1,W2)...P(Wn|W1,W2...Wn-1)
使用n个单词来组成的序列来衡量切分方案的合理性就做N元模型,以上的公式也叫做概率的链规则
由此,可以得到:
如果一个词的出现依赖于它前面的一个词,那么就叫做二元模型
P(S)=P(W1,W2,W3...Wn)=P(W1)P(W2|W1)P(W3|W1,W2)...P(Wn|W1,W2...Wn-1)
=P(W1)P(W2|W1)P(W3|W2)...P(Wn|Wn-1)
以此类推:
如果一个词的出现依赖于它前面的两个词,那么称之为三元模型
如果一个词的出现不依赖于其他词,那么称之为一元模型,比如前文的例子,使用全概率公式计算的就是一元模型。
常用的中文分词工具
1、盘古分词
盘古分词是一个基于.net 平台的开源中文分词组件,提供lucene(.net 版本) 和HubbleDotNet的接口
高效:Core Duo 1.8 GHz 下单线程 分词速度为 390K 字符每秒
准确:盘古分词采用字典和统计结合的分词算法,分词准确率较高。
功能:盘古分词提供中文人名识别,简繁混合分词,多元分词,英文词根化,强制一元分词,词频优先分词,停用词过滤,英文专名提取等一系列功能。
2、IKAnalyzer 开源的轻量级中文分词工具包
IKAnalyzer 是一个开源的,基于java语言开发的轻量级的中文分词工具包。从2006年12月推出1.0版开始,IKAnalyzer已经推出 了3个大版本。最初,它是以开源项目Luence为应用主体的,结合词典分词和文法分析算法的中文分词组件。新版本的IKAnalyzer3.0则发展为 面向Java的公用分词组件,独立于Lucene项目,同时提供了对Lucene的默认优化实现。
还有很多的中文分词工具,这里只是简单的列举了一种,还有一种常见的,并且使用较为广泛的是jieba,有兴趣的读者可以自行去查阅相关资料。
好了,本篇文章就介绍到这里,如有任务疑问,欢迎留言讨论,谢谢。