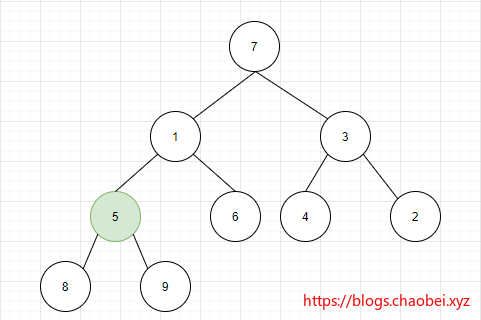
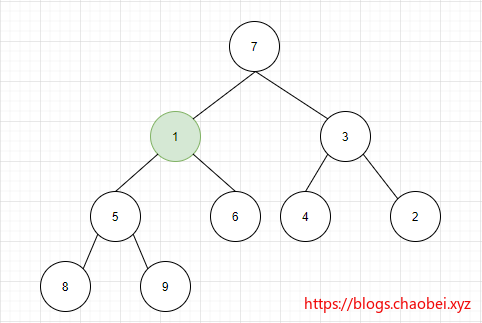
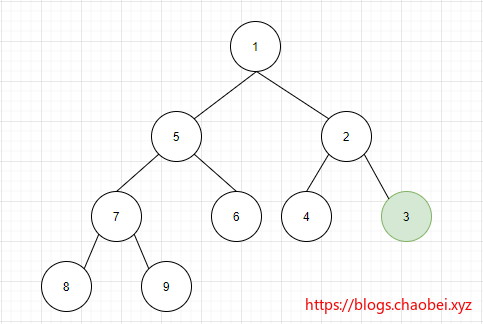
是否记得我们在之前的学习中有学习到二叉树 忘记的小伙伴们请查看：完全二叉树的定义。
https://blogs.chaobei.xyz/archives/shuju2
二叉堆
二叉堆其实就是一个完全二叉树 一起复习一下吧：关于二叉树和满二叉树以及完全二叉树的基本概念。
二叉树
- 每个节点下挂元素不超过2
- 并且元素都是按照一定规律排列的
二叉树规律
按照前人的总结，我们可以得出以下结论。
- 一个深度为K 的二叉树，最多包含节点数
2的k次方-1 - 二叉树指定n 层级所包含的节点数为
2的n-1次方
满二叉树
从字面意思我们可以理解到：这个二叉树它是一种饱和的状态，顾名思义称作是满二叉树。
完全二叉树
除去二叉树的叶子节点，所有节点都包含有两个节点，并且节点都是按照一定顺序排列的，这样的二叉树被称作是完全二叉树
二叉堆类型
在上面我们已经提到过。二叉堆就是一种完全二叉树、二叉树的概念也已经了解到了。当然，现在应该分析二叉堆有有哪些性质
- 最大堆
- 最小堆
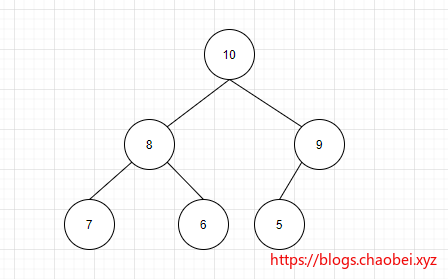
最大堆
最大堆的父节点元素的值都大于等于其两个子元素的值
最小堆
反之，最小堆父节点元素的值，都小于等于其两个子元素的值
二叉堆的堆顶部 则是这个堆序列最大或者最小的元素。
二叉堆的自我调整
二叉堆的自我调整，有以下几种情况：
- 新元素的插入
- 元素的删除
- 构建二叉堆
我们以最上面的最小堆为例，讲述如何将一个元素插入二叉堆、如何删除一个元素、如何来构建一个二叉堆。
插入一个节点
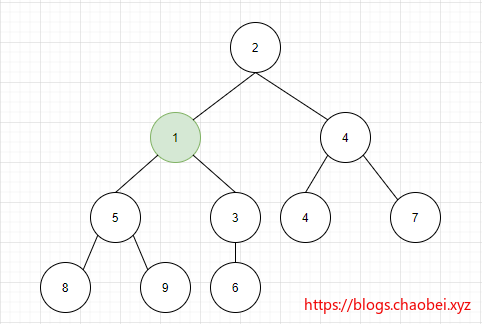
按照上面最小堆的顺序，我这里再插入几个其他元素方便观察。假设这里我插入一个元素1
元素1<元素6 进行上浮。子节点与父节点进行调换位置
元素1<元素3 进行上浮。子节点与父节点进行调换位置
元素1<元素2 进行上浮。到达堆顶部。
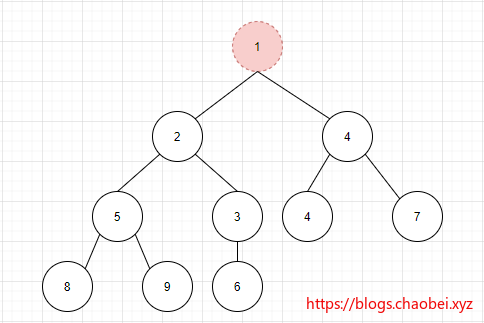
删除一个元素
当前元素与子节点中最小元素进行比较、大于则交换位置下沉
假设我们删除最顶层的元素1
二叉堆为了保证树的结构、将二叉堆里面尾部元素6填充到被删除的位置。
当前元素6 与两个子元素里面最小元素 进行比较。大于则下沉
当前元素6 > 3 进行调换位置。元素6到达尾部。
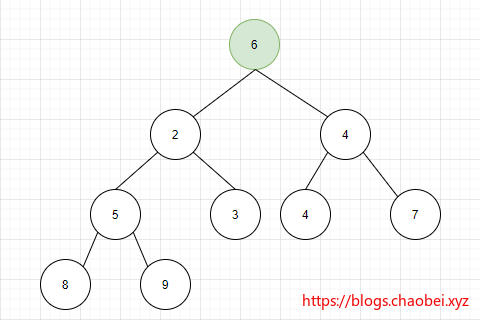
规律：二叉堆的删除元素和新增元素刚好是相反的
构建一个二叉堆
构建二叉堆、其实就是将一个原有的、无序的、完全二叉树给他构建成有序的二叉堆。
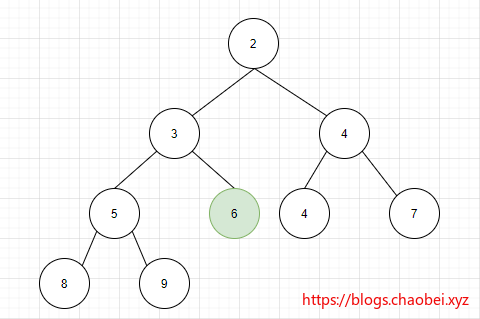
假设我们来构建一个最小堆 我们这里拿到一个无序的完全二叉树如图：
划重点：构建最小堆就是将非叶子节点进行下沉
1、操作元素5 元素5小于元素8 不进行移动
2、操作元素1 元素1小于元素5 不进行移动
3、操作元素7 省略步骤。最终结果如下：
4、操作元素3 省略步骤。最终结果如下：
至此，我们的无序完全二叉树已经变成了一个有序的二叉最小堆了
代码实现
二叉堆虽然是一颗完全二叉树，但是其存储方式是顺序存储，使用的是数组、而不是链式指针。
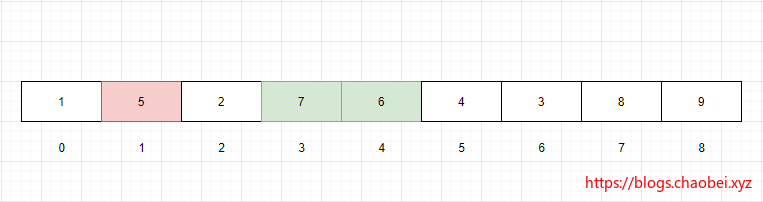
我们可以发现如下规律：
- 父元素左边子元素位置 = 2*父元素下标 + 1
- 父元素右边子元素位置 = 2*父元素下标 + 2
public static void main(String[] args) {
int[] array = {7, 1, 3, 5, 6, 4, 2, 8, 9};
buildBinaryHeap(array);
System.out.println(Arrays.toString(array));
}
public static void buildBinaryHeap(int[] array) {
//除去叶子节点、将每个节点进行下沉操作
for (int i = (array.length - 2) / 2; i >= 0; i--) {
sinking(array, i);
}
}
/**
* 构建二叉堆、让当前元素下沉
*
* @param array 被操作的数组
* @param itemIndex 当前元素下标
*/
public static void sinking(int[] array, int itemIndex) {
//数组长度
int length = array.length - 1;
//父节点值
int parent = array[itemIndex];
//默认操作的是左孩子
int childIndex = 2 * itemIndex + 1;
while (childIndex < length) {
//存在右边子元素、并且右边子元素值小于左边
if (childIndex + 1 < length && array[childIndex + 1] < array[childIndex]) {
//切换到右边元素
childIndex++;
}
//小于等于则无需交换
if (parent <= array[childIndex]) break;
//无需交换、只需要将子元素移动到父元素位置即可
array[itemIndex] = array[childIndex];
itemIndex = childIndex;
//改变左右子元素的下标
childIndex = 2 * itemIndex + 1;
}
//最终将父元素移动到指定位置即可。
array[itemIndex] = parent;
}
代码示例
https://gitee.com/mrc1999/Data-structure
小结
通过本节的学习，应该需要掌握二叉堆这个重要的数据结构、如何将一个完全二叉树构建成一个二叉堆、并且二叉堆在插入元素、和删除元素时候如何将原来的结构保持不变的。这该是我们学习的。
下一节将继续学习二叉堆的堆排序、我们一起加油！
参考
https://mp.weixin.qq.com/s/cq2EhVtOTzTVpNpLDXfeJg