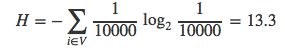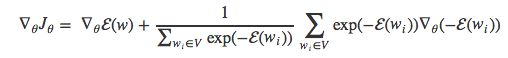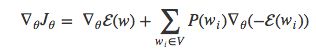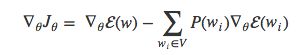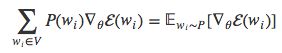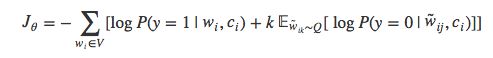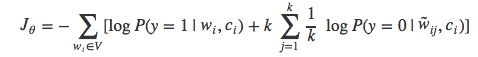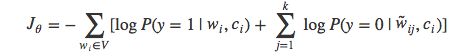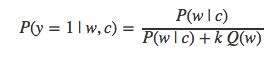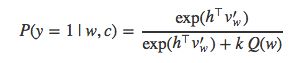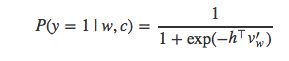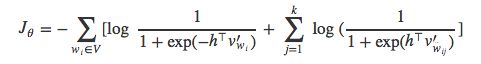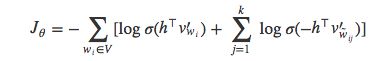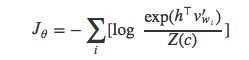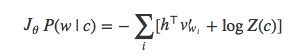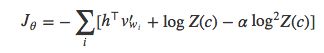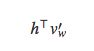漫谈词向量之基于Softmax与Sampling的方法
本文是词向量与表达学习系列的第二篇文章。前一篇文章介绍了词向量模型。
原文: On word embeddings
作者: Sebastian Ruder
译者: KK4SBB 审校:王艺
责编:王艺 若您有想要分享的行业案例、技术笔记、请联系 [email protected]
本文经作者授权CSDN翻译发布,未经允许不得转载。
目录:
- 基于softmax的方法
- Hierarchical Softmax
- Differentiated Softmax
- CNN softmax
- 基于sampling的方法
- Importance Sampling
- Adaptive Importance Sampling
- Target Sampling
- Noise Contrastive Estimation
- Negative Sampling
- Self-Normalisation
- Infrequent Normalisation
- Other Approaches
- 各种方法对比
- 小结
Bengio等人2003年提出的神经语言模型,Collobert和Weston在2008年提出的C&W模型,以及Mikolov等人在2013年提出的word2vec模型。作者认为,降低最后的softmax层的计算复杂度是设计更好词向量模型所面临的主要挑战,同时也是机器翻译(Jean等[10])和语言建模(Jozefowicz等[6])的共性挑战。
本篇文章列举了近几年内新提出的几种替代softmax层的方法。其中一些方法目前还只在语言建模和机器学习中尝试过。关于超参数的讨论将安排在后续的系列文章中介绍。
先来复习一遍上篇文章里用到的符号:假设有一份训练文档集,它包括了T个训练词语w1,w2,w3,⋯,wT,它们构成大小为|V|的词语集合V。语言模型通常只考虑由当前词语wi的左右n个词语组成的上下文ci。每个词语有一个d维的输入词向量vW(即embedding层的词向量)和输出词向量v’W(即softmax层的权重矩阵所表示的词语)。最后,针对模型参数θ来优化目标函数Jθ。
若指定上下文c,用softmax方法计算词语w出现的概率可以用公式表示为:
h是网络倒数第二层的输出向量。为了简化表示,上式中用c表示上下文内容,并且省略了目标词语wt的下标t。为了得到上式的分母部分,需要计算向量h与词典V中每个词语向量之间的内积。因此,计算softmax的代价非常昂贵。
接下来,我们将讨论几种能够近似替代softmax的策略。这些方法可以归纳为基于softmax的和基于sampling的两大类。基于softmax的方法仍旧保留了模型的softmax层,但是通过调整其结构来提高效率。基于sampling的方法则完全抛弃了softmax层,而是优化其它形式的损失函数来代替softmax。
基于softmax的方法
分层Softmax
Hierarchical softmax (H-Softmax)是由Morin和Bengio[3]受到二叉树的启发而提出。H-Softmax本质上是用层级关系替代了扁平化的softmax层,如图1所示,每个叶子节点表示一个词语。于是,计算单个词语概率值的计算过程被拆解为一系列的概率计算,这样可以避免对所有词语进行标准化计算。用H-Softmax替换softmax层之后,词语的预测速度可以提升至少50倍,速度的提升对于低延时要求的实时系统至关重要,比如谷歌新推出的消息应用Allo。
我们可以把原来的softmax看做深度为1的树,词表V中的每一个词语表示一个叶子节点。计算一个词语的softmax概率需要对|V|个节点的概率值做标准化。如果把softmax改为二叉树结构,每个word表示叶子节点,那么只需要沿着通向该词语的叶子节点的路径搜索,而不需要考虑其它的节点。
平衡二叉树的深度是log2(|V|),因此,最多只需要计算log2(|V|)个节点就能得到目标词语的概率值。注意,得到的概率值已经经过了标准化,因为二叉树所有叶子节点组成一个概率分布,所有叶子节点的概率值总和等于1。我们可以简单地验证一下,在图1的根节点(Node o)处,两个分枝的概率和必须为1。之后的每个节点,它的两个子节点的概率值之和等于节点本身的概率值。因为整条搜索路径没有概率值的损失,所以最底层所有叶子节点的概率值之和必定等于1,hierarchical softmax定义了词表V中所有词语的标准化概率分布。
具体说来,当遍历树的时候,我们需要能够计算左侧分枝或是右侧分枝的概率值。为此,给每个节点分配一个向量表示。与常规的softmax做法不同,这里不是给每个输出词语w生成词向量v’w,而是给每个节点n计算一个向量v’n。总共有|V|-1个节点,每个节点都有自己独一无二的向量表示,H-Softmax方法用到的参数与常规的softmax几乎一样。于是,在给定上下文c时,就能够计算节点n左右两个分枝的概率:
![]()
上式与常规的softmax大致相同。现在需要计算h与树的每个节点的向量v’n的内积,而不是与每个输出词语的向量计算。而且,现在只需要计算一个概率值,这里就是偏向n节点右枝的概率值。相反的,偏向左枝的概率值是1−p(right|n,c)
如图2所示,假设已知出现了词语“the”、“dog”、“and”、“the”,则出现词语“cat”的概率值就是在节点1向左偏的概率值、在节点2向右偏的概率以及在节点5向右偏的概率值的乘积。Hugo Lachorelle在他的视频教程中给了更详细的解释。Rong[7]的文章也详细地解释了这些概念,并推导了H-Softmax。
显然,树形的结构非常重要。若我们让模型在各个节点的预测更方便,比如路径相近的节点概率值也相近,那么凭直觉系统的性能肯定还会提升。沿着这个思路,Morin和Bengio使用WordNet的同义词集作为树簇。然而性能依旧不如常规的softmax方法。Mnih和Hinton[8]将聚类算法融入到树形结构的学习过程,递归地将词集分为两个集合,效果终于和softmax方法持平,计算量有所减小。
值得注意的是,此方法只是加速了训练过程,因为我们可以提前知道将要预测的词语(以及其搜索路径)。在测试过程中,被预测词语是未知的,仍然无法避免计算所有词语的概率值。
在实践中,一般不用“左节点”和“右节点”,而是给每个节点赋一个索引向量,这个向量表示该节点的搜索路径。如图2所示,如果约定该位为0表示向左搜索,该位为1表示向右搜索,那词语“cat”的向量就是011。
上文中提到平衡二叉树的深度不超过log2(|V|)。若词表的大小是|V|=10000,那么搜索路径的平均长度就是13.3。因此,词表中的每个词语都能表示为一个平均长度为13.3比特的向量,即信息量为13.3比特。
关于信息量
在信息论中,人们习惯于将词语w概率值的负对数定义为信息量I(w):
I(w)=−log2p(w)
而熵H则是词表中所有词语的信息量的期望值:
H=∑i∈Vp(wi)I(wi)
熵也代表着根据信息的概率分布对信息编码所需要的最短平均编码长度。 抛硬币事件需要用1比特来编码正反两个时间,对于永恒不变的事件则只需0比特。若用平衡二叉树的节点来表示词表中的词语,还是假设词表的大小|V|=10000,词表中词语的概率值均相等,那么熵H与平均搜索路径的长度恰好相等:
之前我们一再强调了树结构的重要性,因为利用好树结构不仅能提升系统的性能,还能加快运算速度。若我们给树加入额外的信息,就能缩短某些携带信息量少的词语的搜索路径。Morin和Bengio就是利用了词表中各个词语出现概率不相等这一信息。他们认为词表中的一些词语出现的概率总是大于其它词语,那这些词语就应该用更短的向量编码。他们所用的文档集(|V|=10000)的熵大约是9.16。
于是,考虑词频之后,文档集中每个词语的平均编码长度从13.3比特减为9.16比特,运算速度也提升了31%。Mikolov等人在他们关于hierarchical softmax的论文[1]里就用到了霍夫曼树,即词频越高的词语编码长度越短。比如,“the”是英语中最常见的词语,那“the”在霍夫曼树中的编码长度最短,词频第二高的词语编码长度仅次于“the”,以此类推。整篇文档的平均编码长度因此降低。
霍夫曼编码通常也被称作熵编码,因为每个词语的编码长度与它的熵几乎成正比。香农通过实验[5]得出英语字母的信息量通常在0.6~1.3之间。假设单词的平均长度是4.5个字母,那么所携带的信息量就是2.7~5.85比特。
再回到语言模型:衡量语言模型好坏的指标perplexity是2H,H表示熵。熵为9.16的unigram模型的perplexity达到29.16=572.0。我们可以直观的理解为,平均情况下用该unigram模型预测下一个词语时,有572个词语是等可能的候选词语。目前,Jozefowicz在2016年的论文中提到最好的模型perplexity=24.2。因为24.6=24.2,所以这个模型平均只需要4.6比特来表示一个词语,已经非常接近香农记录的实验下限值了。这个模型是否能用于改进网络的hierarchical softmax层,仍需要人们进一步探索。
分片Softmax
Chen等人在论文中介绍了一种传统softmax层的变换形式,称作Differentiated Softmax (D-Softmax)。D-Softmax基于的假设是并不是所有词语都需要相同数量的参数:多次出现的高频词语需要更多的参数去拟合,而较少见的词语就可以用较少的参数。
传统的softmax层用到了dx|V|的稠密矩阵来存放输出的词向量表示v′w∈ℝd,论文中采用了稀疏矩阵。他们将词向量v′w按照词频分块,每块区域的向量维度各不相同。分块数量和对应的维度是超参数,可以根据需要调整。
图3中,A区域的词向量维度是dA(这个分块是高频词语,向量的维度较高),B和C区域的词向量维度分别是dB和dC。其余空白区域的值为0。
隐藏层h的输出被视为是各个分块的级联,比如图3中h层的输出是由三个长度分别为dA、dB、dC的向量级联而成。D-Softmax只需计算各个向量段与h对应位置的内积,而不需整个矩阵和向量参与计算。
由于大多数的词语只需要相对较少的参数,计算softmax的复杂度得到降低,训练速度因此提升。相对于H-Softmax方法,D-Softmax的优化方法在测试阶段仍然有效。Chen在2015年的论文中提到D-Softmax是测试阶段最快的方法,同时也是准确率最高的之一。但是,由于低频词语的参数较少,D-Softmax对这部分数据的建模能力较弱。
CNN-Softmax
传统softmax层的另一种改进是受到Kim[3]的论文启发,Kim对输入词向量vw采用了字符级别的CNN模型。相反,Jozefowicz在2016年将同样的方法用于输出词向量v′w,并将这种方法称为CNN-Softmax。如图4所示,如果我们在输入端和输出端加上CNN模型,输出端CNN生成的向量v′w与输入端CNN生成的向量必然不相同,因为输入和输出的词向量矩阵就不一样。
尽管这个方法仍需要计算常规softmax的标准化,但模型的参数却大大的减少:只需要保留CNN模型的参数,不需要保存整个词向量矩阵dx|V|。在测试阶段,输出词向量v′w可以提前计算,所以性能损失不大。
但是,由于字符串是在连续空间内表示,而且模型倾向于用平滑函数将字符串映射到词向量,因此基于字符的模型往往无法区分拼写相似但是含义不同的词语。为了消除上述影响,论文的作者增加了一个矫正因数,显著地缩小了CNN-Softmax与传统方法的性能差距。通过调整矫正因数的维度,作者可以方便地取舍模型的大小与计算性能。
论文的作者还提到,前一层h的输出可以传入字符级别的LSTM模型,这个模型每次预测输出词语的一个字母。但是,这个方法的性能并不令人满意。Ling等人在2014年的论文中采用类类似的方法来解决机器翻译任务,取得了不错的效果。
基于采样的方法
至此,我们所讨论的方法仍旧保持了softmax的结果。然而,基于采样的方法完全摒弃了softmax层结构。后者采用了更方便计算的损失值来逼近softmax的分母项。基于采样的方法也仅在训练阶段有效,在预测阶段仍需要按部就班地计算softmax层,从而得到标准化的概率值。
为了直观地感受softmax的分母对损失值的影响,我们先来推导损失函数Jθ对于模型参数θ的导数。
在训练阶段,我们的目标是使得训练集中每个词语w的交叉熵最小,也就是使得softmax层输出值的负对数取值最小。如果读者对softmax输出值与交叉熵的关系比较模糊,可以参考Karpathy的解释。模型的损失函数可以写成:
为了便于推导,我们将Jθ改写为:
为了与Bengio和Senecal[4,15]使用的符号一致(注意,第一篇论文计算的是梯度的对数,没有负号),用−(w)代替hTv’w。于是得到等式:
在反向传播阶段,我们可以将损失函数对于θ的偏导写为:
![]()
因为logx的导数是1/x,则上式又可以改写为:
![]()
把偏导符号移到求和项里面,得到:
因为exp(x)的导数就是exp(x),于是也可以得到如下形式:
经过变换,得到:
![]()
注意,
![]()
就是词语wi的softmax概率值P(wi)。将其代入上面的等式中得到:
最后,将求和项内的负号移到外面
Bengio和Senécal 2003年的时候提出梯度值可以分解为两个部分:一部分与目标词语w正相关(等式右边的第一项),另一部分与其余所有词语负相关,按照各个词语的出现概率分配权重(等式右边的第二项)。我们可以发现,等式右边的第二项其实就是词表V中所有词语wi的的期望值:
现在大多数基于采样方法的核心都是用简单的过程来近似计算后一项的值。
重要性采样
wm采用蒙特卡洛方法来估计概率分布的期望值E。如果已知网络模型的分布P(w),于是我们就可以从中随机采样m个词语w1,⋯,wm,并用下面的公式计算期望值:
但是,为了实现从概率值分布P中采样,我们必须先计算得到P,而这个过程正是我们想绕开的。于是,我们用另一种类似于P但是采样更方便的分布Q来代替。在语言建模的任务中,直接把训练集的unigram分布作为Q不失为良策。
这就是经典的重要性采样(Importance Sampling)的做法:它使用蒙特卡洛方法得到分布Q来模拟真实的分布P。可是,被采样到的词语w仍然需要计算其概率值P(w)。Bengio和Senécal借助了Liu论文[16]中的思路。
上文提到把Pwi赋值为
的权重,这里我们把权重值改为与Q相关的一个因子。这个因子是
![]()
其中
![]()
我们用r和R是为了避免与Bengio和Senécal论文中的w和W命名冲突。于是期望的估计值公式可以写为:
若是采样的数量越少,估计的分布与真实分布差别越大。如果样本数量非常少,在训练过程中网络模型的分布P可能与unigram的分布Q差异很大,会导致模型发散,因此我们需要调整到合适的样本数量。Bengio和Senécal的论文中介绍了一种快速选择样本数量的方法。最终的运算速度比传统的softmax提升了19倍。
自适应重要性采样
Bengio和Senécal 2008年的论文中提到,在重要性采样的方法中用更复杂的分布来替代unigram分布Q对改善模型的帮助并不大,他们尝试了bigram和trigram,但常规的n-gram分布与训练得到的神经语言模型似乎差别挺大。于是,他们提出了自适应的n-gram分布来更好地拟合目标分布P。他们将bigram和unigram融合,融合的系数用SGD的方法训练得到,最终使得融合后的分布Q与目标分布P的KL距离最小。他们的实验显示这种方法能使速度提升100倍。
目标采样
2015年,Jean在论文里提到将自适应重要性采样用于机器翻译任务。为了使该方法能更好地适应GPU内存资源有限的情况,他们限制了待采样词语的数量。他们将训练集分区,每个分区仅保留放固定数量的样本,形成词表的一个子集V’。
这就意味着训练集的每个分区i可以用独立的分布Qi,该分区内所有词语的概率值均相等,而Qi将分区i之外其余词语的概率值设为零。
噪声对比估计
噪声对比估计(Noise Contrastive Estimation)是Mnih和Teh[18]发明的一种比重要性采样更稳定的采样方法,因为某些情况下重要性采样存在导致分布Q与P分道扬镳的风险。NCE不是直接估计某个词语的概率值。相反,它借助一个辅助的损失值,从而实现了正确词语概率值最大化这一目标。
我们在上一篇文章中提到,Collobert和Weston(2008)采用的pair-wise排序准则是将正确的样本排在其它样本之前。NCE的想法与其类似:训练一个模型来区分目标词语与噪声。于是,待解决的问题就由预测正确的词语简化为一个二值分类器任务,分类器试图将正确的词语与其它噪声样本中区分开来,如图4所示:
对于每个词语wi,它的前n个词语wt-1, ……, wt-n+1表示为wi的语境ci。然后从含有噪声的分布Q中生成k个噪声样本w̃ik。参照重要性采样的方法,这里也可以从训练数据的unigram分布中采样。由于分类器需要用到标签数据,我们把语境 ci 对应的所有正确的词语wi标记为正样本(y=1),其余的噪声词语w̃ik作为负样本(y=0)。
接着,用逻辑回归模型来训练样本数据:
由于计算所有噪声样本的期望
时仍需要对词表V中的词语求和,得到标准化的概率值,于是可以采用蒙特卡洛方法来估算:
简化为:
实际上,我们是从两个不同的分布中采样数据:正样本是根据语境c从训练数据集Ptrain中采样,而负样本从噪声分布Q中采样获得。因此,无论是正样本还是负样本,其概率值都可以表示成上述两种分布带权重的组合,权重值对应于来自该分布的样本值:
于是,样本来自于Ptrain的概率值可以表示为条件概率的形式:
这个式子可以被简化为:
![]()
由于不知道Ptrain(待计算项),我们就用P来代替:
当然,样本为负样本的概率值就是P(y=0|w,c)=1−P(y=1|w,c)。值得注意的是,已知c求词语w出现的概率值P(w|c)的计算方法实际上就是softmax的定义:
![]()
因为分母只与h相关,h的值与c相关(假设V不变),那么分母可以简化为Z(c)来表示。softmax就变为下面的形式:
![]()
为了求解Z(c),还是需要对V中所有词语出现的概率值求和。NCE则用了一个小技巧巧妙地绕开:即把标准化后的分母项Z(c)当作模型的待学习参数。Mnih和Teh(2012)、Vaswani等[20]在论文中都把Z(c)的值固定设为1,他们认为这样不会对模型的效果造成影响。Zoph[19]则认为,即使训练模型,最终得到Z(c)的值也是趋近于1,并且方差很小。
若是我们把上面softmax等式中的Z(c)项改为常数1,等式就变为:
![]()
再把上面的式子代入求解P(y=1|w,c)P(y=1|w,c),得到:
继续把上式代入到逻辑回归的目标函数中,得到:
![]()
NCE方法有非常完美的理论证明:随着噪声样本k的数量增加,NCE导数趋近于softmax函数的梯度。Mnih 和 Teh (2012) 认为抽取25个噪声样本就足以达到常规softmax方法的效果,速度能提升大约45倍。Chris Dyer撰写的笔记[21]对NCE方法进行了更详细的解释。
NCE方法也存在一个弊端,由于每个正样本词语w对应的噪声样本各不相同,这些负样本就无法以稠密矩阵的形式存储,也就无法快速地计算稠密矩阵的乘法,这就削弱了GPU的优势。Jozefowicz et al. (2016) 和 Zoph et al. (2016) 各自分别提出了在同一个批数据中共享噪声样本的想法,于是可以发挥GPU的稠密矩阵快速运算的优势。
NCE与IS的相似性
jozefowicz认为NCE与IS的相似点不仅在于它们都是基于采样的方法,而且相互之间联系非常紧密。NCE等价于解决二分类任务,他认为IS问题也可以用一个代理损失函数来描述:IS相当于用softmax和交叉熵损失函数来优化解决多分类问题。他觉得IS是多分类问题,可能更适用于自然语言的建模,因为它迭代更新受到数据和噪声样本的共同作用,而NCE的迭代更新则是分别作用。事实上,Jozefowicz等人选用IS作为语言模型并且取得了最佳的效果。
负采样
负采样(Negative Sampling)可以被认为是NCE的一种近似版本。我们之前也提到过,随着样本数量k的增加,NCE近似于softmax的损失。由于NEG的目标是学习高质量的词向量表示,而不是降低测试集的perplexity指标,于是NEG对NCE做了简化。
NEG也采用逻辑回归模型,使得训练集中词语的负对数似然最小。再回顾一下NCE的计算公式:
NEG与NCE的关键区别在于NEG以尽可能简单的方式来估计这个概率值。为此,上式中计算量最大的kQ(w) 项被置为1,于是得到:
![]()
当k=|V|并且Q是均匀分布时,kQ(w)=1成立。此时,NEG等价于NCE。我们将kQ(w)设置为1,而不是其它常数值的原因在于,P(y=1|w,c)P(y=1|w,c)可以改写为sigmoid函数的形式:
如果我们再把这个等式代入之前的逻辑回归损失函数中,可以得到:
进一步简化后得到:
假设
![]()
最终得到:
为了与Mikolov et al. (2013)论文中的符合保持一致,h要用vwI替换,v’wi要用v’wO替换,vwij
要用v’wi替换。另外,与Mikolov所使用的目标不同,我们在三个方面做了修改:a)对整个文档集做优化,b)最小化负对数似然,而不是最大化对数似然,c)用蒙特卡洛方法估计期望值
若想了解更多NEG的细节,可以参考Goldberg 和 Levy 的笔记[22]。
我们发现,仅当k=|V|并且Q是均匀分布时,NEG才等价于NCE。在其它情况下,NEG只是近似于NCE,也就是说前者不会直接优化正确词语的对数似然,所以不适合用于自然语言建模。NEC更适用于训练词向量表示。
自标准化
尽管Devlin[23]提出的自标准化方法不是基于采样的,但他的想法能给我们带来不少启发。上一节我们提到,若将NCE损失函数的Z(c)这一项值设为1,模型就相当于是自标准化。这一特性帮我们节省了大量计算Z(c)标准化的资源。
损失函数Jθ的目标是最小化训练数据中所有词语的负对数似然:
经过变换得到:
如果能限制模型的Z(c)=1或是logZ(c)=0,那么就不必计算Z(c)项中复杂的标准化了。于是,Devlin建议给损失函数加一项平方误差的惩罚项,使得logZ(c)尽可能逼近与0:
等价于:
其中,系数α用来平衡模型的准确率和自标准化计算。经过这样的改造,Z(c)的值就会趋近于1。在Devlin2014年那篇有关机器翻译系统的论文中,他们在解码阶段将softmax的分母项置为1,仅计算分子项和惩罚项:
据他们称,自标准化方法的速度提升了将近15倍,而BLEU得分相比于常规的方法只降低了一点点。
低频标准化
Andreas 和 Klein[11] 认为只需要对一部分训练样本做标准化,就能取得近似于自标准化的效果。于是他们提出了低频标准化(Infrequent Normalisation)的方法,对惩罚项降采样,使之变为一种基于采样的方法。
先把上文中的损失函数Jθ分解为两部分:
然后就可以对第二项进行降采样,得到下面的公式:
![]()
其中,γ控制采样率。Andreas 和 Klein (2015) 认为IF不但采纳了NCE和自标准化两者的优点,即不需要对所有训练样本进行标准化计算,而且也能很好的取舍模型的准确率和标准化估计值的准确程度。据他们称,当只对1/10的训练数据进行标准化时,速度可以提升将近10倍,且没有明显的效果下降。
其它的方法
除了上述介绍的几种方法来近似技术或者避免计算softmax的分母项Z(c)之外,另一些方法是针对
项做优化。比如,Vijayanarasimhan在论文[12]中提出了快速的局部敏感哈希算法近似计算
![]()
但是,尽管Vijayanarasimhan的方法在测试阶段加快了模型的预测速度,但是在训练阶段速度优化的效果不明显。
各种方法对比
上文中已经总结了多种基于softmax和基于采样的方法,这些方法都能极大地提升运算效率。这一节中,我们将多这些方法做个比较。
| 方法 | 速度提升值 | 训练阶段是否有提升 | 测试阶段是否有提升 | 模型效果(小数据集) | 模型效果(大数据集) | 参数数量 |
|---|---|---|---|---|---|---|
| softmax | 1x | - | - | 非常好 | 非常差 | 100% |
| 分层softmax | 25x(50-100x) | 否 | - | 非常差 | 非常好 | 100% |
| 分片softmax | 2x | 否 | 否 | 非常好 | 非常好 | <100% |
| CNN softmax | - | 否 | - | - | 一般 | 30% |
| 重要性采样 | (19x) | 否 | - | - | - | 100% |
| 自适应重要性采样 | (100x) | 否 | - | - | - | 100% |
| 目标采样 | 2x | 否 | - | 好 | 差 | 100% |
| 噪声对比采样 | 8x(45x) | 否 | - | 非常好 | 非常差 | 100% |
| 负采样 | (50-100x) | 否 | - | - | - | 100% |
| 自标准化 | (15x) | 否 | - | - | - | 100% |
| 低频标准化 | 6x(10x) | 否 | - | 非常好 | 好 | 100% |
如上表所示,几乎每种方法在不同的数据集或是不同的场景下都有利弊。对于语言建模,常规的softmax方法在小数据集上的效果仍然非常好,比如Penn Treebank,有时甚至在中等规模数据集上的表现也不错,比如Gigaword,但是它在大规模数据集上的效果就很差,例如1B Word Benchmark。目标采样。相反,分层采样和低频标准化等方法在大规模数据集上的效果非常好。
分片softmax在小数据集和大数据集上的效果都不错,并且它是唯一做到在测试阶段速度提升的方法。分层softmax方法在小数据集上的表现较差,但是它的速度最快,单位时间内处理的训练样本数量也最多。NCE适用于大数据集,但多数情况下效果不如其它方法。负采样方法不擅长语言建模问题,它更适用于学习词向量表示,比如用在经典的word2vec中。
最后,如果你想选用上述的方法,TensorFlow已经实现了其中一部分基于采样的方法,并且比较了部分方法的差异。
小结
总而言之,学习词语的表达是一个非常宽泛的领域,很多因素都会影响最终的表达效果。在上一篇文章中,我们介绍了常用模型的结构。在这篇文章中,我们从softmax层切入,深入探究和比较了多种方法。下一篇文章我们将会介绍GloVe方法。
参考文献
Mikolov, T., Chen, K., Corrado, G., & Dean, J. (2013). Distributed Representations of Words and Phrases and their Compositionality. NIPS, 1–9.
Mikolov, T., Corrado, G., Chen, K., & Dean, J. (2013). Efficient Estimation of Word Representations in Vector Space. Proceedings of the International Conference on Learning Representations (ICLR 2013), 1–12.
Morin, F., & Bengio, Y. (2005). Hierarchical Probabilistic Neural Network Language Model. Aistats, 5.
Bengio, Y., & Senécal, J.-S. (2003). Quick Training of Probabilistic Neural Nets by Importance Sampling. AISTATS. http://doi.org/10.1017/CBO9781107415324.004
Shannon, C. E. (1951). Prediction and Entropy of Printed English. Bell System Technical Journal, 30(1), 50–64. http://doi.org/10.1002/j.1538-7305.1951.tb01366.x
Jozefowicz, R., Vinyals, O., Schuster, M., Shazeer, N., & Wu, Y. (2016). Exploring the Limits of Language Modeling. Retrieved from http://arxiv.org/abs/1602.02410
Rong, X. (2014). word2vec Parameter Learning Explained. arXiv:1411.2738, 1–19. Retrieved from http://arxiv.org/abs/1411.2738
Mnih, A., & Hinton, G. E. (2008). A Scalable Hierarchical Distributed Language Model. Advances in Neural Information Processing Systems, 1–8. Retrieved from http://papers.nips.cc/paper/3583-a-scalable-hierarchical-distributed-language-model.pdf
Chen, W., Grangier, D., & Auli, M. (2015). Strategies for Training Large Vocabulary Neural Language Models. Retrieved from http://arxiv.org/abs/1512.04906
Jean, S., Cho, K., Memisevic, R., & Bengio, Y. (2015). On Using Very Large Target Vocabulary for Neural Machine Translation. Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th International Joint Conference on Natural Language Processing (Volume 1: Long Papers), 1–10. Retrieved from http://www.aclweb.org/anthology/P15-1001
Andreas, J., & Klein, D. (2015). When and why are log-linear models self-normalizing? Naacl-2015, 244–249.
Vijayanarasimhan, S., Shlens, J., Monga, R., & Yagnik, J. (2015). Deep Networks With Large Output Spaces. Iclr, 1–9. Retrieved from http://arxiv.org/abs/1412.7479
Kim, Y., Jernite, Y., Sontag, D., & Rush, A. M. (2016). Character-Aware Neural Language Models. AAAI. Retrieved from http://arxiv.org/abs/1508.06615
Ling, W., Trancoso, I., Dyer, C., & Black, A. W. (2016). Character-based Neural Machine Translation. ICLR, 1–11. Retrieved from http://arxiv.org/abs/1511.04586
Bengio, Y., & Senécal, J.-S. (2008). Adaptive importance sampling to accelerate training of a neural probabilistic language model. IEEE Transactions on Neural Networks, 19(4), 713–722. http://doi.org/10.1109/TNN.2007.912312
Liu, J. S. (2001). Monte Carlo Strategies in Scientific Computing. Springer. http://doi.org/10.1017/CBO9781107415324.004
Gutmann, M., & Hyvärinen, A. (2010). Noise-contrastive estimation: A new estimation principle for unnormalized statistical models. International Conference on Artificial Intelligence and Statistics, 1–8. Retrieved from http://www.cs.helsinki.fi/u/ahyvarin/papers/Gutmann10AISTATS.pdf
Mnih, A., & Teh, Y. W. (2012). A Fast and Simple Algorithm for Training Neural Probabilistic Language Models. Proceedings of the 29th International Conference on Machine Learning (ICML’12), 1751–1758.
Zoph, B., Vaswani, A., May, J., & Knight, K. (2016). Simple, Fast Noise-Contrastive Estimation for Large RNN Vocabularies. NAACL.
Vaswani, A., Zhao, Y., Fossum, V., & Chiang, D. (2013). Decoding with Large-Scale Neural Language Models Improves Translation. Proceedings of the 2013 Conference on Empirical Methods in Natural Language Processing (EMNLP 2013), (October), 1387–1392.
Dyer, C. (2014). Notes on Noise Contrastive Estimation and Negative Sampling. Arxiv preprint. Retrieved from http://arxiv.org/abs/1410.8251
Goldberg, Y., & Levy, O. (2014). word2vec Explained: Deriving Mikolov et al.’s Negative-Sampling Word-Embedding Method. arXiv Preprint arXiv:1402.3722, (2), 1–5. Retrieved from http://arxiv.org/abs/1402.3722
Devlin, J., Zbib, R., Huang, Z., Lamar, T., Schwartz, R., & Makhoul, J. (2014). Fast and robust neural network joint models for statistical machine translation. Proc. ACL’2014, 1370–1380.