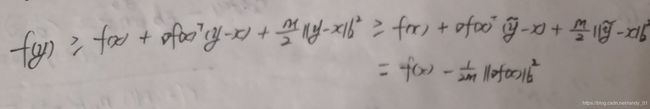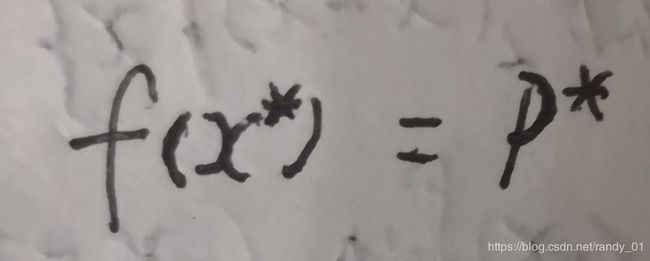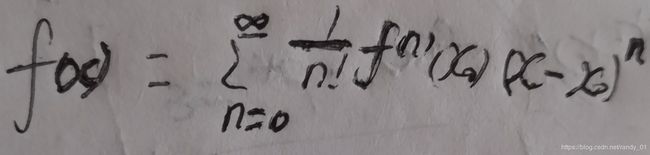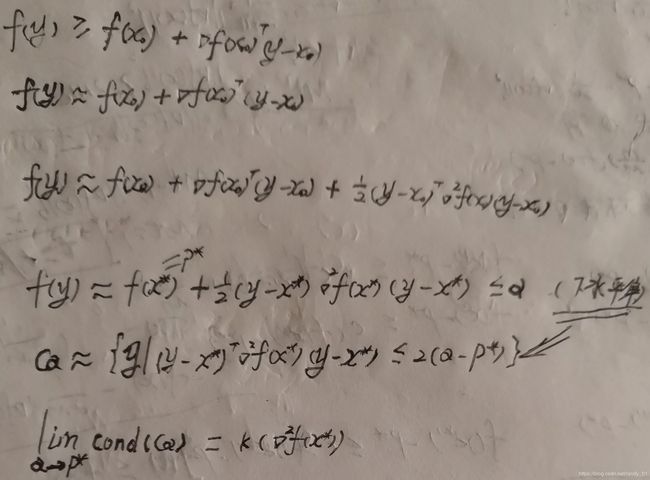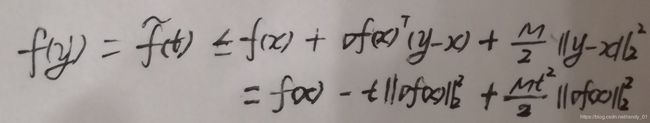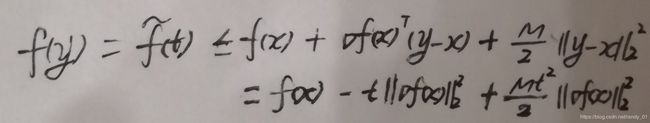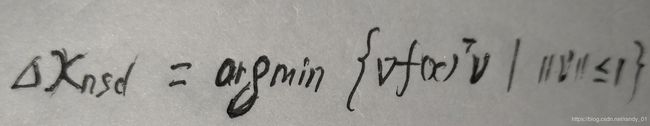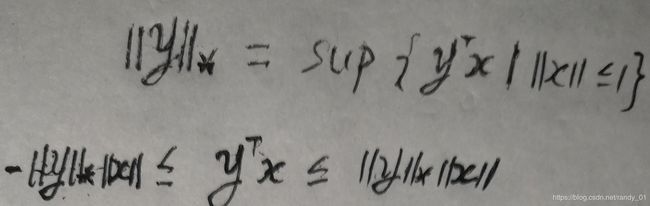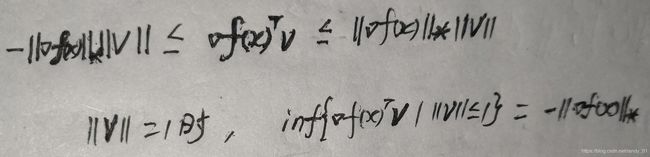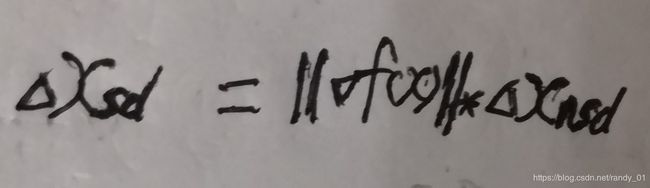从数学角度探究梯度下降算法的本质
以数据驱动的AI,根本任务有两个:①建立系统的评价准则或者规则;②寻找最优的归纳偏置。找到最优的归纳偏置关键在于参数的优化算法。目前机器学习的参数优化算法集中在遗传算法,模拟退火,SGD等。1996年非常具有代表性的论文lasso在损失函数的多准则构建上做出了杰出贡献。这篇论文属于基础学科研究领域,对后来的AI理论发展起到了非常大的推进作用。在众多的AI公开课中,很少有从数学角度深入研究这个课题的,基本都是直接结论的讲解。比如码农们比较关心深度学习参数的调优,可能认为基础理论研究不务实。而事实上只有基础理论研究的突破才是人工智能向前推动的源动力。本文从最底层的数学角度探究梯度下降的本质,从中可以给出很多工程改进的启示。本文结构安排如下:
一、预备数学知识;
二、参数搜索算法;
三、最速梯度下降算法;
四、梯度下降算法改进。
第一部分:预备数学知识
1.1 强凸性
这部分的知识是总纲,统领后面的理论推导。本部分属于《凸优化》算法部分,基础是微积分和凸函数的一阶条件。当机器学习的损失函数满足强凸性时,对于下水平集s,有以下关系:
根据强凸性的一阶条件,设y是x附近的点,有以下关系:
这个很好理解,根据微分的性质就可以搞定。如果一个函数是凸的,还具有以下性质:
 ,这个代表参数搜索方向与正梯度的夹角总是锐角,如果小于0表示参数搜索方向与负梯度的夹角是锐角,其中y - x表示搜索方向向量。
,这个代表参数搜索方向与正梯度的夹角总是锐角,如果小于0表示参数搜索方向与负梯度的夹角是锐角,其中y - x表示搜索方向向量。
设z是线段xy之间的一点,有:
根据前面的Hessian矩阵的上下界,得到以下不等式关系:
上述不等式对于属于下水平集的任意x都成立!接下来的处理很关键了,先处理左半部分。把左半部分的不等式看成是关于y的函数,我们可以先求出它的下界,即让关于y的偏导数=0,得出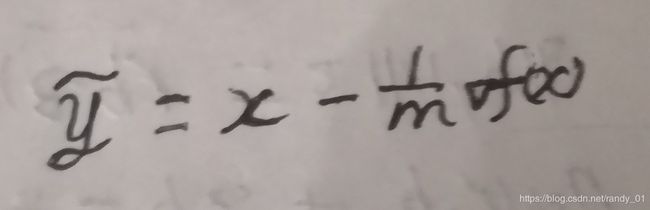 ,带入不等式中得出它的下界:
,带入不等式中得出它的下界: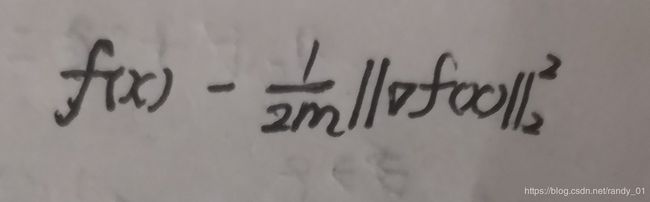 。因此有以下关系:
。因此有以下关系:
由于对于任意的x成立,设函数的最优解满足下列关系:
那么就有下列不等式关系了:
设参数经过每次迭代后与理论最优解间的误差为 ,那么可以推导出以下关系:
,那么可以推导出以下关系:
1.2 下水平级的条件数
1.21 椭球的条件数
梯度下降算法的迭代次数严重依赖下水平集的条件数,或者最优解的Hessian矩阵的条件数,稍后将会看到结论。这部分补充条件数的求解方法。先求解椭球的宽度,然后才能求出条件数。设有一个单位方向向量q,z属于椭球的元素,那么椭球的宽度按照以下方法求解:
那么条件数为:
从上面的例子可以看出,条件数更大的意义是定义了各向异性或者离心率。比如上述椭球的条件数就是椭球特征矩阵的条件数,如果条件数很小接近1的话,他就趋近于圆球了。
1.22 下水平集的条件数
这里先补充一下基础知识。研究梯度下降算法的收敛性主要手段是推断最优解附近的一阶条件和二阶条件。在傅立叶变换那篇文章中有如下结论:
这个公式的含义是函数的幂级数收敛于f(x),其展开式为Taylor级数分解。定义域为x0的邻域,意为我们用这个公式推导时,主要看最优解附近的点的一阶条件或者二阶条件。什么时候看一阶条件?当运用微分思维元素无限接近x0时,此时一阶条件也就是Taylor的一阶展开成立,更确切地,此时函数收敛于Taylor的一阶展开。当参数为x0附近时,运用二阶条件更为有效。当x0为最优解时,一阶导数为0。请看下面的公式:
最后部分,当参数迭代到最优解附近时(此时还没有无限接近最优解),运用泰勒二阶展开式,在根据下水平集定义得到下水平集的椭球表达式(以最优解为中心的椭球)。参数搜索的几何意义是椭球上的元素向负梯度方向投影,椭球不断收缩直到接近最优解。当函数值趋近于最优解时,此时的下水平集条件数与最优解的Hessian矩阵条件数趋同。
第二部分:梯度下降的两个参数搜索算法
有了第一部分的铺垫,接下来该进入正题了。这部分主要讲述两个参数搜索算法,尤其是回溯直线搜索算法,在工程中具有非常大的意义。在进行参数搜索时,首先要定义参数搜索方向,这部分需要方向导数与梯度以及微分的基本功(可以参考我的“导数与黎曼积分”博客,保证切入点和课本不同)。方向定义好了后才能定义步长,然后探讨影响迭代次数的主要因素,最后从影响因素中寻找改进方案。这是寻找最优参数的基本方法论指导。根据这个研究方法,在接下来的两小节里,我们先固定搜索方向,即按照梯度下降迭代,然后我们主要讨论下降步长问题,在第三部分再讨论最速下降方向问题。
首先定义一下通用的参数搜索算法步骤:
2.1 精确直线搜索
看到这个名字,你就该想到它的下降步长是固定的。之所以成为直线搜索,是因为每次迭代后数据基本呈现直线关系下降(大致)。先引入几个符号:
t表示步长, 表示参数搜索方向,比如X1 - X0表示从初始点经过一次迭代后的方向向量。在迭代过程中我们用如下公式来表达参数更新:
表示参数搜索方向,比如X1 - X0表示从初始点经过一次迭代后的方向向量。在迭代过程中我们用如下公式来表达参数更新:
 ,它等同于
,它等同于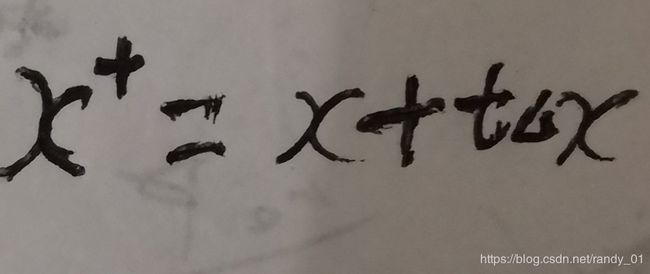 ,即
,即 。在讨论精确直线搜索时,我们要用到第一部分的预备知识,强凸性的不等式部分。设
。在讨论精确直线搜索时,我们要用到第一部分的预备知识,强凸性的不等式部分。设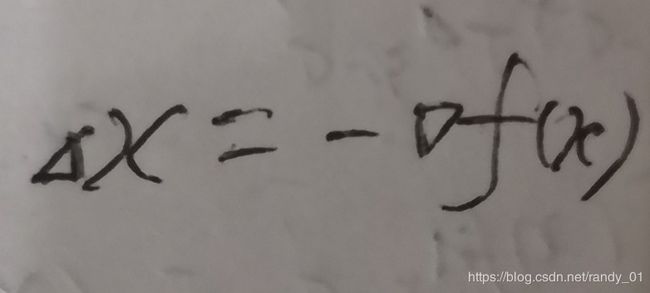 ,
, ,根据第一部分的不等式④我们得到如下关系(把它看成关于t的函数):
,根据第一部分的不等式④我们得到如下关系(把它看成关于t的函数):
这个不等式恒成立的条件是最后一部分的最小值大于等于f(t)。对t求导数 = 0得到t = 1 / M,带入进入得到
我们继续推导
这个过程反应了每步迭代的误差变化,我们看到误差收缩系数是 C = 1 - m / M,它是一个<1的系数。当迭代结束时,最终参数的函数值与极小值的误差应该不大于我们设定的误差精度,于是得到如下重要结论:
进一步整理得到
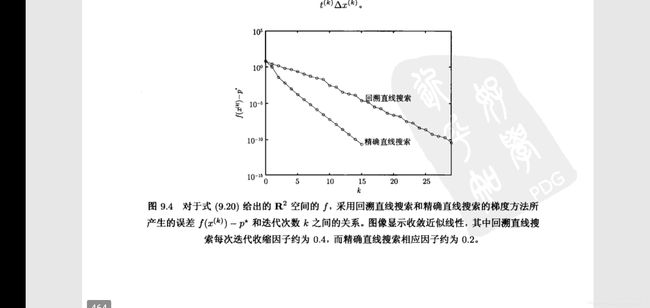
≈式成立的条件是当m / M很小时,也就是下水平集或者最优解的Hessian矩阵的条件数很糟糕。我们看到此时的迭代次数几乎与条件数成正比,K的影响因素包括初始值的选择,误差精度以及条件数。
前面的精确直线搜索算法,步长是固定的,t = 1/M。这里的M取值不一定非得是Hessian矩阵的最大特征值,比如可以取值为最大特征值与最小特征值的均值。M取值为最大特征值是最保守的做法,不提倡。而且精确直线搜索最大的意义是给回溯直线搜索算法提供借鉴参考,当数据集非常庞大时,回溯直线搜索算法更有效。
2.2 回溯直线搜索算法
2.21 回溯直线搜索算法
相比于精确直线搜索算法,这个算法更加适合于大型工程。这个算法的基本流程在通用算法的基础上增加如下内容:
 一般取值<0.5,
一般取值<0.5, 取值为0.8时是精准搜索,取值0.1时是粗糙搜索。建议取值≥0.5。研究回溯直线搜索算法主要手段是Taylor一阶展开,因为参数越接近最优解,步长越低,当无限接近时,一阶条件成立。设搜索方向为v,那么以下公式成立:
取值为0.8时是精准搜索,取值0.1时是粗糙搜索。建议取值≥0.5。研究回溯直线搜索算法主要手段是Taylor一阶展开,因为参数越接近最优解,步长越低,当无限接近时,一阶条件成立。设搜索方向为v,那么以下公式成立: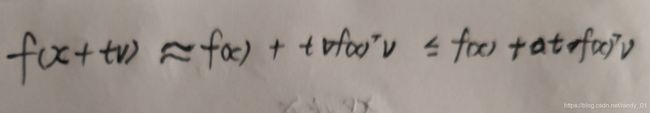 ,由于是下降方向,所以方向导数<0,所以后面的不等式成立,这就是回溯直线搜索算法的收敛条件。这个算法为何会引入α元素,下面会有更详细的解释:
,由于是下降方向,所以方向导数<0,所以后面的不等式成立,这就是回溯直线搜索算法的收敛条件。这个算法为何会引入α元素,下面会有更详细的解释:
下面的短划线是曲线函数的线性外推,上面的短划线斜率是线性外推的α倍。f的下降落在两者之间是最佳结果。从图中看,t的取值范围为0~t0。线性外推的理解其实很简单,只要你真正理解了微分的本质。所以当α取值<1.0,当阿尔法取值为0.3左右时效果会比较好。最终的结论是,t的收敛值有两个,一个是t = 1,另一个是t > βt0。
2.22 收敛条件判断
我们还是以负梯度为搜索方向,那么前年提到的收敛条件就是这个: 。这个条件是如何得来的?依然是根据强凸性推导出的,请看:
。这个条件是如何得来的?依然是根据强凸性推导出的,请看:
对比这两个不等式,我们发现当 时,可以推导出前面的收敛条件。因为当t满足这个条件时我们才会推导出这个收敛条件,过程略。下面看看收敛条件的判定:
时,可以推导出前面的收敛条件。因为当t满足这个条件时我们才会推导出这个收敛条件,过程略。下面看看收敛条件的判定:
 由于t的收敛取值为并集∪关系,所以才会出现min函数。后面的推导与精确直线搜索相同,最终得到收敛公式:
由于t的收敛取值为并集∪关系,所以才会出现min函数。后面的推导与精确直线搜索相同,最终得到收敛公式:
至此,我们总结一下梯度下降算法:
2.23 步长的一个确定方法
回溯直线搜索算法给了我们重要的启示,即在迭代过程中,步长随着参数接近最优解时逐渐减少。所以如果步长不应该是固定的,如果过发可能会越过最优解,过小迭代次数又会增多。在工程中如何设置好的步长?在最开始迭代的时候,我们可以把步长设置得大一些,当迭代次数超过阈值时,让步长随着迭代次数衰减是一个不错的想法。如下所示:
其中,![]() 为衰减速率,为取得较为精确的结果,可以设定为0.9以上,比如0.95。t0通常情况下设置为1,索引i+1为迭代次数,MAX为步长衰减的迭代次数阈值,可以根据工程情况调节,比如设置为100。整个max函数的含义是当迭代次数低于阈值时,步长不衰减,当超过阈值后,步长开始呈固定底数的指数倍衰减,幂为迭代次数与MAX的差值。
为衰减速率,为取得较为精确的结果,可以设定为0.9以上,比如0.95。t0通常情况下设置为1,索引i+1为迭代次数,MAX为步长衰减的迭代次数阈值,可以根据工程情况调节,比如设置为100。整个max函数的含义是当迭代次数低于阈值时,步长不衰减,当超过阈值后,步长开始呈固定底数的指数倍衰减,幂为迭代次数与MAX的差值。
2.24 举例
这部分主要是想说明,当工程量比较大时,回溯直线搜索算法的思想占据主导,并且把α和β的值设置大一些是最佳选择。比如α取值为0.3,β取值为0.5或者0.7。举一个最简单的例子吧
第三部分:最速梯度下降算法
我们提过了,影响参数优化的因素主要有步长,搜索方向。而梯度下降方法经过第二部分收敛条件的讨论我们知道,这种方法严重依赖下水平集的条件数。而最优解附近的下水平集其实是以最优解为中心的椭球。在解决了步长因素后,这部分我们着重讨论最快的下降方向。很多人会认为梯度是最快的下降方向,这个结论没错,用方向导数和梯度的关系可以解释。但是这个结论仅限于欧氏空间,不适用于一般的范数(想深入了解距离,范数,内积这些概念,需要进修数学专业,比如泛函数分析)。这部分的论述稍微抽象一点儿,不过也不是很难,因为这毕竟是应用数学范畴。
3.1 最快下降方向
当参数无限接近最优解时,根据微分的几何意义,或者Taylor的一阶展开式我们得到了图中的公式。后面的部分就是邻近参数间的函数值差,最快的下降方向当然是让这这差值最大化了。由于是下降方向,所以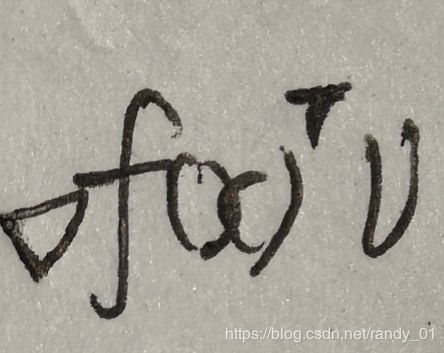 是<0的,也就是搜索方向与负梯度的夹角是锐角。所以最后结果是让这个方向导数值最小,它是关于v的线性函数,斜率<0,理论上可以让v无限大然后取得最小值。但是这是不可能的,因此我们限定v的范数为1,最后我们定义标准的规范化的最速下降方向为
是<0的,也就是搜索方向与负梯度的夹角是锐角。所以最后结果是让这个方向导数值最小,它是关于v的线性函数,斜率<0,理论上可以让v无限大然后取得最小值。但是这是不可能的,因此我们限定v的范数为1,最后我们定义标准的规范化的最速下降方向为
注意:这里v的范数并不是2阶范数,也不是1阶范数,而是一般范数。关于它的几何意义稍后解释,现在的任务是当v为何值时上式取得极小值?在《凸优化》的第四章里有关于对偶范数的介绍,先回顾一下:
后面是对偶元素的内积取值范围。把x换成v,y换成梯度,先按照l-2范数推导。有下面的关系式:
至此,我们可以得到 是
是 的单位球向
的单位球向 方向的投影值为
方向的投影值为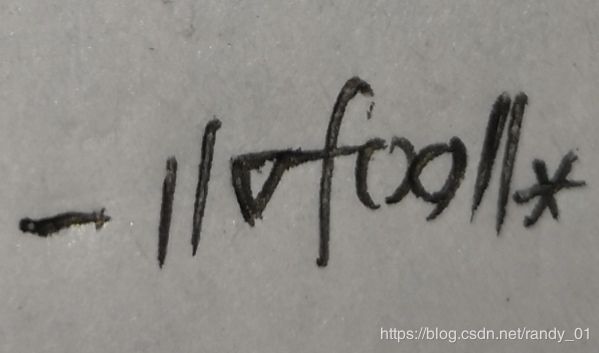 的搜索方向。x的规范化搜索方向就是单位球上的v,我们的目标就是确定范数为1的v的方向。在实际应用中,我们通常会使用非规范化的搜索方向,即进行下面的处理:
的搜索方向。x的规范化搜索方向就是单位球上的v,我们的目标就是确定范数为1的v的方向。在实际应用中,我们通常会使用非规范化的搜索方向,即进行下面的处理:
现在从几何角度来解读一下这个公式:规范化的搜索方向其实是v与梯度呈180度夹角,投影值是梯度的对偶范数的相反数。于是我们得到了非规范化的几何意义(在欧式空间,针对2阶范数,一个元素的对偶范数就是二阶范数):
在欧式空间把v的长度拉伸原梯度的二阶范数倍。对于一般范数,我们有 。这时邻近参数间的函数值差为
。这时邻近参数间的函数值差为 。至此,算是彻底明白了经常挂在嘴边儿的梯度下降是如何得来的,它的隐含条件是在欧氏空间中。
。至此,算是彻底明白了经常挂在嘴边儿的梯度下降是如何得来的,它的隐含条件是在欧氏空间中。
前面的讨论,v是按照2范数来进行的。也可以按照1阶范数,或者无穷阶范数。几何意义如下:
这部分对于没有进修过泛函数分析的人理解起来可能有点儿困难。一个元素的p阶范数以及它的对偶范数的阶数存在如下关系:1/p + 1/q = 1。比如p为2时,它的对偶范数和本身相同,p为1时,对偶范数为∞阶。这就是数学,每一部的证明和推理都需要严谨。关于最速梯度下降算法的收敛性讨论省略了,和之前的结论是一致的。接下来我们进入到本篇文章的核心部分。
第四部分:梯度下降算法的改进
根据前三节的探讨,相信大多数人对参数优化算法有了初步的了解,现在我们运用之前的知识来讨论如何改进算法。根据收敛性我们知道迭代次数严重依赖下水平集的条件数,除此之外从推导的迭代次数公式中我们看到,随机梯度下降算法也依赖于初始值的选定以及误差精度的制定。在工程中工程师最关心的是初始值的选定。这些基本都是手动调节的,理论上不好证明。但是对于下水平集的条件数却可以用理论研究来改进。改进的依据就是降低下水平集的条件数,让它越小越好。一个基本的想法就是参数替换,请看如下推导:
把参数替换为原来参数的椭球,2次p范数:
替换后的几何意义:
关于p的取值是一个学术难题,只能找到近似矩阵,但是不总是能找到,这个需要继续深入研究。
总结:梯度下降算法的研究,主要取决于下水平集的条件数,如果不是很糟糕的话,就可以集中精力调节下降步长,初始值。如果很糟糕,需要降低条件数,论述完毕!