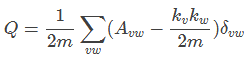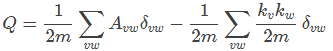基于GN算法的网络通联关系社团发现(Python)
一、什么是社团?
社团是具有某些共同特征的人相聚而成的互益组织。随着社交网络的快速发展,人类社会对网络的依赖程度也越来越高,特别是基于网络的社交工作层出不穷,通过网络分析人类现实社会关系的可能性和可行性大大增强。
二、什么是GN算法?
GN 算法是由Grivan和Newman所提出的一种图论经典算法。基本思想就是:社团之间成员的联系多,不同社团的成员之间联系少。社团之间所存在的少数几个连接是社团间通信的瓶颈,是社团间通信时数据流的必经之路。按照某种形式的通信关系并且寻找到具有最高通信经过的边,该边就应该是连接不同社团的通道。将这样的边全部去掉后,就获得了社团的最高分解形式。为了衡量一条边具有的最高通信经过的程度,引入了边介数(betweenness)的概念,这是在点介数基础上的推广应用。边介数指的是所有节点对之间的虽短路径中经过该边的最短路径数。
GN算法的主要步骤:计算网络中每条边的边介数,去掉边介数最大的那条边。重复进行直至网络中没有任何边存在。
但GN算法也存在2点不足。一是该算法无法预知网络最终应该分裂成多少社团;二是计算速度缓慢,在一个具有m条边和n个节点的图中计算出每条边的介数所需时间为O(mn)。
为了解决第一个问题,Newman在2004年的一片论文中又提出了模块度(Modularity)的概念。
三、什么是模块度?
模块度又称模块化度量值,是目前常用的一种衡量网络社区结构强度的方法,其定义为“Modularity is the fraction of the edges that fall within the given groups minus the expected such fraction if edges were distributed at random.”(来自wiki),其公式为:
这个式子是合并后的形式,在理解的过程中应当将中括号去掉,做一个分配率的变化,如下图。
模块度值Q的大小主要取决于网络中节点的社区分配C,即网络的社区划分情况,可以用来定量的衡量网络社区划分质量,其值越接近1,表示网络划分出的社区结构的强度越强,也就是划分质量越好。因此可以通过最大化模块度Q来获得最优的网络社区划分。
这个公式解释一下,A是网络的邻接矩阵的一个元素,v和w是网络中的两个点,如果这两个点之间有边存在的话,Avw=1,否则等于0。而δvw的取值定义为:若两者在同一个社区内,δvw为1,否则为0。kv和kw的代表i点和j点的度,m为网络中边的总数。这个式子表示在同一社区内的边的数量占所有边数量的比例,乘以1/2则是因为在邻接矩阵中每条边都计算了两次。
后一个式子表示的是将对网络的边进行随机分配,需要将每条边切断一分为二,这样m条边就会产生2m个末梢点,随机的将这2m个末梢点进行连接,包括同一节点拥有的末梢点的自连接。这样可以保持每个节点原有的度不变的条件下,可以得到一个完全随机网络。在这样的随机网络下,任意两点v、w连接边数的期望值是kvkw/2m。
总的来说,模块度的大小就是社区内部的总边数和网络中总边数的比例减去一个期望值,该期望值是将网络设定为随机网络时同样的社区分配所形成的社区内部的总边数和网络中总边数的比例的大小。
通过这样的计算得出模块值Q的取值范围为[-0.5,1),有可能取到负值。
四、有了Q值之后的GN算法
有了Q值之后,我们只要将整个网络不停地分割下去,每次分割都计算一次Q值,最终,输出Q值最高时的社团分类就行了。
具体算法为:
1.计算当前网络的边介数和Q值,并存储Q值和当前网络中社团分割情况;
2.出去边介数最高的边;
3.计算当前网络的Q值,如果此Q值比原来的大,则将现在的Q值和网络中社团分割情况存储更新,否则,进行下一次网络分割;
4.所有边分割完毕,返回当前的Q值和社团分割情况。
Python算法实现等下篇再更新