支持向量机算法简介以及利用以及python的实现
支持向量机算法简介(Python)
一、支持向量机方法简介
支持向量机(SVM)是一种常见的分类方法,在机器学习领域,是一个有监督的学习模型,通常用来进行模式识别、分类以及回归分析。SVM的核心思想主要为两点:
- 它基于结构风险最小化理论之上在特征空间中构建最优超平面,使得学习器得到全局最优化,并且在整个样本空间的期望以某个概率满足一定上界。
- 它是针对线性可分情况进行分析,对于线性不可分的情况,通过使用非线性映射算法将低维输入空间线性不可分的样本转化为高维特征空间使其线性可分,从而使得高维特征空间采用线性算法对样本的非线性特征进行线性分析成为可能。
二、支持向量机的原理
2.1 类别的划分方法
支持向量机作为一个二分类的方法,其原理就是寻找一个超平面将两个不同的类别(1和-1类)分开。如下图所示:
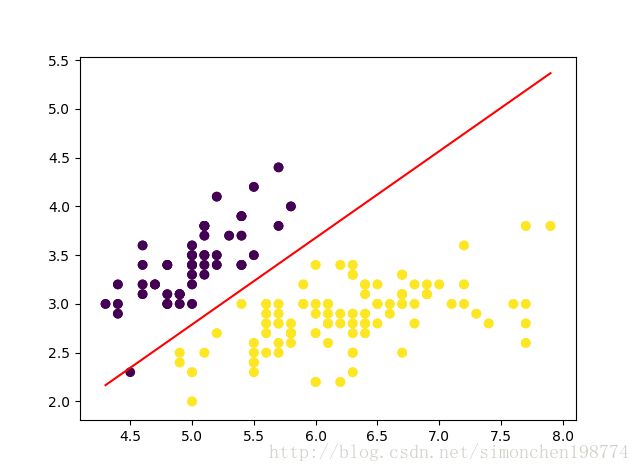
上图中紫色和黄色分别对应两种不同的分类,而红线 f ( x ) = w x T + b f(x)=wx^T+b f(x)=wxT+b就是用于分割两种类型的超平面。当 f ( x ) = 0 f(x)=0 f(x)=0则x是位于超平面上的点,当 f ( x ) > 0 f(x)>0 f(x)>0则x是位于超平面以上,是1的分类,而当 f ( x ) < 0 f(x)<0 f(x)<0则位于超平面以下,是-1的分类。
2.2 函数间隔与几何间隔
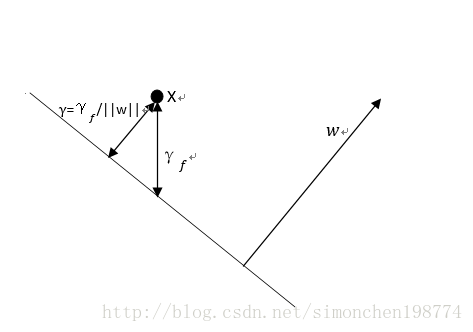
接下来的问题是,如何确定这个超平面呢?从直观上而言,这个超平面应该是最适合分开两类数据的直线。而判定“最适合”的标准就是这条直线离直线两边的数据的间隔最大。在这里我们引入函数间隔这个概念,在超平面 f ( x ) = w x T + b f(x)=wx^T+b f(x)=wxT+b已经确定的情况下, ∣ ∣ w x T + b ∣ ∣ ||wx^T+b|| ∣∣wxT+b∣∣就是点到超平面的距离。而且当类别y与 f ( x ) = w x T + b f(x)=wx^T+b f(x)=wxT+b正负性相同时,说明分类是正确的。反之,则说明分类是错误的。于是函数间隔可以定义为 γ f = y f ( x ) \gamma_f=yf(x) γf=yf(x), 但如图所示函数间隔并不是点到直线的垂直距离,要客观的反映点到函数的距离,我们引入了几何距离这个概念。 γ = y f ( x ) ∣ ∣ w ∣ ∣ \gamma=\frac{yf(x)}{||w||} γ=∣∣w∣∣yf(x),其中 ∣ ∣ w ∣ ∣ = w T w ||w||=w^Tw ∣∣w∣∣=wTw为w的二阶范数,表示的是向量的长度, w ∣ ∣ w ∣ ∣ \frac{w}{||w||} ∣∣w∣∣w则表示单位向量。
2.2 最大间隔分类器
根据支持向量机的特性,当样本特征到超平面的几何距离越大,分类的确信度也越大。因此最大间隔分类器就是指使这个间隔最大的目标函数,即 m a x ( γ ) = m a x ( y f ( x ) ∣ ∣ w ∣ ∣ ) max(\gamma)=max(\frac{yf(x)}{||w||}) max(γ)=max(∣∣w∣∣yf(x))。可以看出该目标函数由分子 y f ( x ) yf(x) yf(x)与分母 ∣ ∣ w ∣ ∣ ) ||w||) ∣∣w∣∣)组成。为了使计算简单,我们将分子固定为1,这时上述目标函数转换成了
(1) m a x ( 1 ∣ ∣ w ∣ ∣ ) s . t y ( w T x + b ) > = 1 max(\frac{1}{||w||})\qquad s.t \quad y(w^Tx+b)>=1 \tag 1 max(∣∣w∣∣1)s.ty(wTx+b)>=1(1)
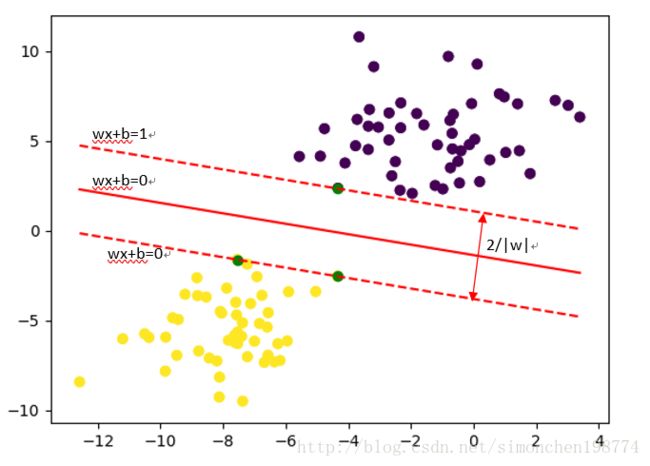
如下图所示,中间的实现平面就是超优平面。两条虚线边界的间隔为 γ = 2 ∣ ∣ w ∣ ∣ \gamma=\frac{2}{||w||} γ=∣∣w∣∣2,在这两条虚线上的绿色点就是支持向量。对于支持向量,满足 y f ( x ) = y ( w T x + b ) = 1 yf(x)=y(w^Tx+b)=1 yf(x)=y(wTx+b)=1。对于所有非支持向量的样本,必须满足 y f ( x ) = y ( w T x + b ) > 1 yf(x)=y(w^Tx+b)>1 yf(x)=y(wTx+b)>1
三、目标函数的求解
为了计算需要,我们可以将公式(1)等价转换为公式(2)
(2) m i n ( 1 2 ∣ ∣ w ∣ ∣ 2 ) s . t y ( w T x + b ) > = 1 min(\frac{1}{2}||w||^2)\qquad s.t \quad y(w^Tx+b)>=1 \tag 2 min(21∣∣w∣∣2)s.ty(wTx+b)>=1(2)
到这个形式以后,就可以很明显地看出来,它是一个凸优化问题,或者更具体地说,它是一个二次优化问题——目标函数是二次的,约束条件是线性的。这个问题可以用任何现成的 QP (Quadratic Programming) 的优化包进行求解。但虽然这个问题确实是一个标准的 QP 问题,但是它也有它的特殊结构,通过 Lagrange Duality 变换到对偶变量 (dual variable) 的优化问题之后,可以找到一种更加有效的方法来进行求解,而且通常情况下这种方法比直接使用通用的 QP 优化包进行优化要高效得多。
也就说,除了用解决QP问题的常规方法之外,还可以应用拉格朗日对偶性,通过求解对偶问题得到最优解,这就是线性可分条件下支持向量机的对偶算法,这样做的优点在于:一者对偶问题往往更容易求解;二者可以自然的引入核函数,进而推广到非线性分类问题。
至于上述提到,关于什么是Lagrange duality?简单地来说,通过给每一个约束条件加上一个 Lagrange multiplier(拉格朗日乘值),即引入拉格朗日对偶变量,如此我们便可以通过拉格朗日函数将约束条件融和到目标函数里去(也就是说把条件融合到一个函数里头,现在只用一个函数表达式便能清楚的表达出我们的问题):
(3) L ( b , w , α ) = 1 2 ∣ ∣ w ∣ ∣ 2 − ∑ i = 1 n α i ( y i ( w T x i + b ) − 1 ) L(b,w,\alpha)=\frac{1}{2}||w||^2-\sum_{i=1}^{n}\alpha_i(y_i(w^Tx_i+b)-1) \tag3 L(b,w,α)=21∣∣w∣∣2−i=1∑nαi(yi(wTxi+b)−1)(3)
然后令
θ ( w ) = m a x ( L ( b , w , α ) ) α i > = 0 \theta(w)=max( L(b,w,\alpha))\qquad\alpha_i>=0 θ(w)=max(L(b,w,α))αi>=0
容易验证,当某个约束条件不满足时,例如 y i ( w T x i + b ) < 1 y_i(w^Tx_i+b)<1 yi(wTxi+b)<1,那么显然有 θ = ∞ \theta=\infty θ=∞(只要 α \alpha α为无穷即可)。而当所有约束条件都满足时,该问题其实也就转化为了对\theta(w)求最小值。具体写起来,目标函数变为:
(4) m i n w , b θ = m i n w , b m a x α i > = 0 L ( w , b , α ) = p ∗ min_{w,b}\theta=min_{w,b}max_{\alpha_i>=0}L(w,b,\alpha)=p^*\tag4 minw,bθ=minw,bmaxαi>=0L(w,b,α)=p∗(4)
这里用 p ∗ p^* p∗表示这个问题的最优值,且和最初的问题是等价的。如果直接求解,那么一上来便得面对w和b两个参数,而又是不等式约束,这个求解过程不好做。不妨把最小和最大的位置交换一下,变成:
(5) m a x α i > = 0 m i n w , b L ( w , b , α ) = d ∗ max_{\alpha_i>=0}min_{w,b}L(w,b,\alpha)=d^*\tag5 maxαi>=0minw,bL(w,b,α)=d∗(5)
交换以后的新问题是原始问题的对偶问题,这个新问题的最优值用 d ∗ d^* d∗来表示。而且有 d ∗ ≤ p ∗ d^*≤p^* d∗≤p∗,在满足KTT条件的情况下,这两者相等,这个时候就可以通过求解对偶问题来间接地求解原始问题。
KTT条件为如下所示:
α i ( y i ( w T x i + b ) − 1 ) = 0 i = 1 , 2 … … n \alpha_i(y_i(w^Tx_i+b)-1)=0 \quad i=1,2……n αi(yi(wTxi+b)−1)=0i=1,2……n
∇ L ( w , b ) = 0 \nabla L(w,b)=0 ∇L(w,b)=0
接下来,我们就根据公式(6)对公式(5)列出的对偶问题求解,可以得出:
∂ L ∂ w = 0 ⇒ w i = ∑ i = 1 n α i y i x i \frac{\partial L}{\partial w}=0\quad \Rightarrow w_i=\sum_{i=1}^{n}\alpha_i y_i x_i ∂w∂L=0⇒wi=i=1∑nαiyixi (6) ∂ L ∂ w = 0 ⇒ ∑ i = 1 n α i y i = 0 \frac{\partial L}{\partial w}=0 \quad \Rightarrow \sum_{i=1}^{n}\alpha_i y_i =0\tag6 ∂w∂L=0⇒i=1∑nαiyi=0(6)
将公式(6)代入公式(3)得到:
(7) L ( b , w , α ) = ∑ i = 1 n α i − 1 2 ∑ i , j = 1 n α i α j y i y j x i T x j L(b,w,\alpha)=\sum_{i=1}^{n}\alpha_i-\frac{1}{2}\sum_{i,j=1}^{n}\alpha_i \alpha_j y_i y_j {x_i}^T x_j\tag7 L(b,w,α)=i=1∑nαi−21i,j=1∑nαiαjyiyjxiTxj(7)
这是公式(5)的对偶问题转化为了:
m a x ( ∑ i = 1 n α i − 1 2 ∑ i , j = 1 n α i α j y i y j x i T x j ) max(\sum_{i=1}^{n}\alpha_i-\frac{1}{2}\sum_{i,j=1}^{n}\alpha_i \alpha_j y_i y_j {x_i}^T x_j) \quad max(i=1∑nαi−21i,j=1∑nαiαjyiyjxiTxj) (8) s t . α i > = 0 i = 1 , 2...... n , ∑ i , j = 1 n α i y i = 0 st.\quad \alpha_i>=0 \quad i=1,2......n ,\quad \sum_{i,j=1}^{n}\alpha_i y_i=0\tag8 st.αi>=0i=1,2......n,i,j=1∑nαiyi=0(8)
在这里需要指出i的是当我们将分类平面的函数 y ( w T x + b ) y(w^Tx+b) y(wTx+b),将w用 α \alpha α替代,就可以得到
(9) f ( x ) = ∑ i = 1 n α i y i < x i , x > + b f(x)=\sum_{i=1}^{n}\alpha_i y_i<x_i,x>+b\tag9 f(x)=i=1∑nαiyi<xi,x>+b(9)
这里的形式的有趣之处在于,对于新点 x的预测,只需要计算它与所有点的内积即可 < x i , x > <x_i,x> <xi,x>,这一点至关重要,是之后使用 Kernel 进行非线性推广的基本前提。此外,所谓 Supporting Vector 也在这里显示出来——事实上,所有非Supporting Vector 所对应的系数 α \alpha α都是等于零的,因此对于新点的内积计算实际上只要针对少量的 α \alpha α不为零“支持向量而不是所有的训练数据即可。用公式表示为:
i f α > 0 , y f ( x ) = 1 if \alpha>0, yf(x)=1 ifα>0,yf(x)=1
(10) i f α = 0 , y f ( x ) > 1 if \alpha=0, yf(x)>1\tag{10} ifα=0,yf(x)>1(10)
为什么非支持向量对应的等于零呢?直观上来理解的话,就是这些“后方”的点——正如我们之前分析过的一样,对超平面是没有影响的,由于分类完全有超平面决定,所以这些无关的点并不会参与分类问题的计算,因而也就不会产生任何影响了。
四、非线性问题求解
事实上,大部分时候数据并不是线性可分的,这个时候满足这样条件的超平面就根本不存在。在上文中,我们已经了解到了SVM处理线性可分的情况,那对于非线性的数据SVM咋处理呢?对于非线性的情况,SVM 的处理方法是选择一个核函数 κ(⋅,⋅) ,通过将数据映射到高维空间,来解决在原始空间中线性不可分的问题。具体来说,在线性不可分的情况下,支持向量机首先在低维空间中完成计算,然后通过核函数将输入空间映射到高维特征空间,最终在高维特征空间中构造出最优分离超平面,从而把平面上本身不好分的非线性数据分开。如下图所示,一堆数据在二维空间线性不可分,于是我们将其映射到三维空间,发现其在三维空间中是线性可分分的。
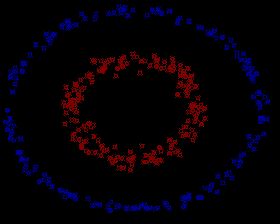
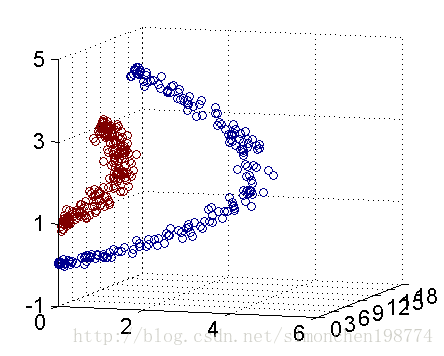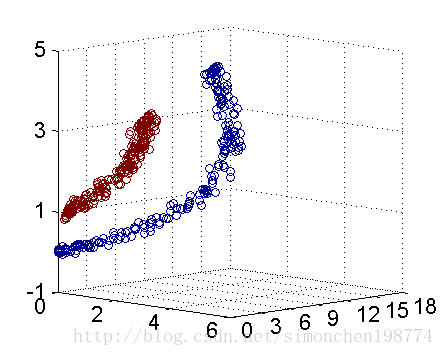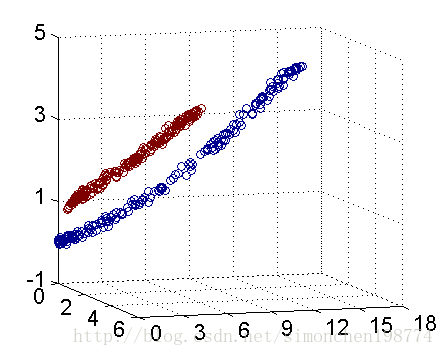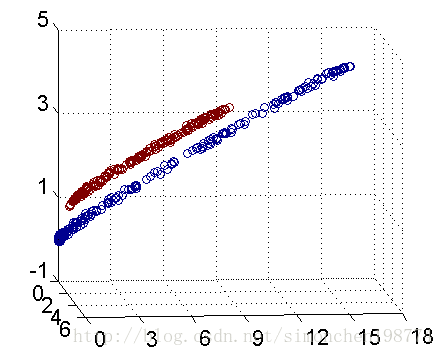
而在我们遇到核函数之前,如果用原始的方法,那么在用线性学习器学习一个非线性关系,需要选择一个非线性特征集,并且将数据写成新的表达形式,这等价于应用一个固定的非线性映射,将数据映射到特征空间,在特征空间中使用线性学习器,因此,考虑的假设集是这种类型的函数:
(11) f ( x ) = ∑ i = 1 n w i ϕ i ( x ) + b f(x)=\sum^{n}_{i=1}w_i\phi_{i}(x)+b \tag{11} f(x)=i=1∑nwiϕi(x)+b(11)
我们将映射后的高维函数带入公式9可以得到:
(12) f ( x ) = ∑ i = 1 n α i y i < ϕ ( x i ) , ϕ ( x ) > + b f(x)=\sum_{i=1}^{n}\alpha_i y_i<\phi(x_i),\phi(x)>+b\tag{12} f(x)=i=1∑nαiyi<ϕ(xi),ϕ(x)>+b(12)
如果我们能找到一种函数K,使得 K ( x i , x ) = < ϕ ( x i ) , ϕ ( x ) > K(x_i,x)=<\phi(x_i),\phi(x)> K(xi,x)=<ϕ(xi),ϕ(x)>,那我们称这种函数为核函数
目前比较常用的核函数为(1)多项式核(2)高斯核,其中多项式和为:
多项式核 K p o l y ( x , x i ) = ( x x i + 1 ) d K_{poly}(x,x_i)=(xx_i+1)^d Kpoly(x,xi)=(xxi+1)dd为多项式阶数
高斯和 K g a u s s ( x , x i ) = − ( x − x i ) 2 / 2 σ 2 K_{gauss}(x,x_i)=-(x-x_i)^2/2\sigma^2 Kgauss(x,xi)=−(x−xi)2/2σ2
五、过拟合处理
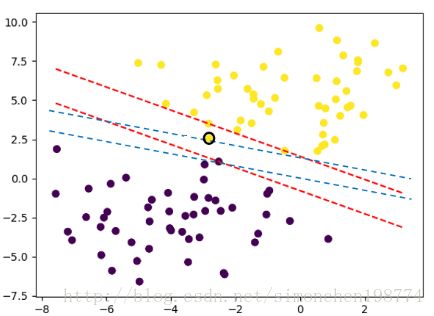
在之前的几章中,我们都是假定数据集都是线性可分的。即便不是线性可分,当我们用kernel函数将其映射到高维之后,仍然可以找到一个超平面,能够将数据分开。不过在实际运用的绝大部分情况中,有一些点(比如下图中黑圈内的点)和正常位置比有一定的偏移。由于本身构成超平面的点就是由少数点组成的,因此个别离群的点会对结果造成很大的影响。
如上图所示,由于带黑圈的黄点会使整个分割的margin变小,从而导致分辨能力变弱。因此我们必须设计出一定的容错机制,使得像这样的偏离点不至于影响分割平面的生成。这时,我们必须要有容错机制。即允许该点存偏离原先的分割区间,这个偏差可以记成 ξ \xi ξ,也叫做松弛变量。原来的约束条件$ y(w^Tx+b)>=1$则变成了
(13) y ( w T x + b ) > = 1 − ξ y(w^Tx+b)>=1 -\xi \tag{13} y(wTx+b)>=1−ξ(13)
在引入了松弛变量以后,原先的目标函数则变为了
(2) m i n ( 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 n ξ ) s . t y ( w T x + b ) > = 1 − ξ min(\frac{1}{2}||w||^2+C\sum_{i=1}^n\xi)\qquad s.t \quad y(w^Tx+b)>=1-\xi \tag 2 min(21∣∣w∣∣2+Ci=1∑nξ)s.ty(wTx+b)>=1−ξ(2)
此时原对偶问题就变成了 m a x ( ∑ i = 1 n α i − 1 2 ∑ i , j = 1 n α i α j y i y j x i T x j ) max(\sum_{i=1}^{n}\alpha_i-\frac{1}{2}\sum_{i,j=1}^{n}\alpha_i \alpha_j y_i y_j {x_i}^T x_j) \quad max(i=1∑nαi−21i,j=1∑nαiαjyiyjxiTxj) (8) s t . C > = α i > = 0 i = 1 , 2...... n , ∑ i , j = 1 n α i y i = 0 st.\quad C>= \alpha_i>=0 \quad i=1,2......n ,\quad \sum_{i,j=1}^{n}\alpha_i y_i=0\tag8 st.C>=αi>=0i=1,2......n,i,j=1∑nαiyi=0(8) 当 α = 0 \alpha=0 α=0时该点在两超平面外 当 α = C \alpha=C α=C时该点在两超平面内 当 0 < α < C 0<\alpha<C 0<α<C时该点在两超平面上
六、支持向量机的实现
import numpy as np
import matplotlib.pyplot as plt
def get_kernel_value(X,Xi,kernel_option):
numSamples=X.shape[0]
kernel_value=np.mat(np.zeros((numSamples,1)))
if kernel_option[0]=='linear':
kernel_value=X*Xi.T
elif kernel_option[0]=='rbf':
sigma=kernel_option[1]
if sigma==0:
sigma=1
for j in range(numSamples):
diff=np.abs(Xi-X[j,:])
kernel_value[j]=np.exp(diff*diff.T/(-2*sigma**2))
else:
raise NameError('No such kind of kernel')
return kernel_value
def get_kernel_matrix(X,kernel_option):
numSamples=X.shape[0]
kernel_matrix=np.mat(np.zeros((numSamples,numSamples)))
for i in range(numSamples):
kernel_matrix[:,i]=get_kernel_value(X,X[i,:],kernel_option)
return kernel_matrix
class SVM:
def __init__(self,toler,C,kernel_option=('linear',0)):
self.toler=toler
self.C=C
self.b=0
self.kernel=kernel_option
self.error_cache=[]
self.alphas=[]
self.kernel_matrix=[]
self.trainX=[]
self.trainY=[]
def error_calcul(self, k):
output_k = np.multiply(self.alphas, self.trainY).T*self.kernel_matrix[:,k]+self.b
error_k=output_k-self.trainY[k]
return error_k
def updateError(self,k):
error=self.error_calcul(k)
if self.alphas[k]<self.C and self.alphas[k]>0:
self.error_cache[k]=[1,error]
else:
self.error_cache[k] = [0, error]
def select_alpha_j(self,i,error_i):
#self.error_cache[i] = [1, error_i]
candidateAlphaList=np.nonzero(self.error_cache[:,0].A)[0]
maxStep=0;j=0;error_j=0
if len(candidateAlphaList)>1:
for k in candidateAlphaList:
if k==i:
continue
error_k=self.error_calcul(k)
if abs(error_i-error_k)>maxStep:
maxStep=abs(error_i-error_k)
j=k
error_j=error_k
else:
j=int(np.random.uniform(0,len(self.trainX)))
error_j=self.error_calcul(j)
return j,error_j
def inner_loop(self,i):
error_i=self.error_calcul(i)
if (self.trainY[i]*error_i<-self.toler) and (self.alphas[i]<self.C) or \
(self.trainY[i] * error_i >self.toler) and (self.alphas[i] > 0):
j,error_j=self.select_alpha_j(i,error_i)
alpha_i_old=self.alphas[i].copy()
alpha_j_old=self.alphas[j].copy()
if self.trainY[i]!=self.trainY[j]:
L=max(0,self.alphas[j]-self.alphas[i])
H=min(self.C,self.C+self.alphas[j]-self.alphas[i])
else:
L = max(0, self.alphas[j] +self.alphas[i]-self.C)
H=min(self.C,self.alphas[j] +self.alphas[i])
if L==H:
return 0
similarity=2*self.kernel_matrix[i,j]-self.kernel_matrix[i,i]-self.kernel_matrix[j,j]
if similarity>=0:
return 0
self.alphas[j]=alpha_j_old-self.trainY[j]*(error_i-error_j)/similarity
if self.alphas[j]>H:
self.alphas[j]=H
if self.alphas[j]<L:
self.alphas[j]=L
if abs(self.alphas[j]-alpha_j_old)<0.00001:
self.updateError(j)
return 0
self.alphas[i]=alpha_i_old+self.trainY[i]*self.trainY[j]*(alpha_j_old-self.alphas[j])
b1=self.b-error_i-self.trainY[i]*(self.alphas[i]-alpha_i_old)*self.kernel_matrix[i,i]-self.trainY[j]*(self.alphas[j]-alpha_j_old)*self.kernel_matrix[i,j]
b2=self.b-error_j-self.trainY[i]*(self.alphas[i]-alpha_i_old)*self.kernel_matrix[i,j]-self.trainY[j]*(self.alphas[j]-alpha_j_old)*self.kernel_matrix[j,j]
if(0<self.alphas[i]) and (self.alphas[i]<self.C):
self.b=b1
elif(0<self.alphas[j]) and (self.alphas[j]<self.C):
self.b=b2
else:
self.b=(b1+b2)/2
self.updateError(j)
self.updateError(i)
return 1
else:
return 0
def fit(self,X,Y,max_iter=100):
trainX=np.mat(X)
trainY=np.mat(np.atleast_2d(Y)).T
numSamples=X.shape[0]
self.trainX=trainX
self.trainY=trainY
self.alphas=np.mat(np.zeros((numSamples,1)))
self.error_cache=np.mat(np.zeros((numSamples,2)))
self.kernel_matrix=get_kernel_matrix(trainX,self.kernel)
entire_set=True
alphaPairsChanged=0
iter=0
while iter<max_iter and (entire_set==True or alphaPairsChanged>0):
alphaPairsChanged=0
if entire_set:
for i in range(numSamples):
alphaPairsChanged+=self.inner_loop(i)
print ('iter:%d entire set,alpha pairs changed:%d'%(iter,alphaPairsChanged))
iter+=1
else:
nonBoundaryList=np.nonzero((self.alphas.A>0)*(self.alphas.A<self.C))[0]
for i in nonBoundaryList:
alphaPairsChanged+=self.inner_loop(i)
print('iter:%d non boundary,alpha pairs changed:%d' % (iter, alphaPairsChanged))
iter+=1
if entire_set:
entire_set=False
elif alphaPairsChanged==0:
entire_set=True
def predict(self,test_x):
testX=np.mat(test_x)
numSamples=testX.shape[0]
supportVectorIndex=np.nonzero((self.alphas.A>0))[0]
supportVectors=self.trainX[supportVectorIndex]
supportVectorLabels=self.trainY[supportVectorIndex]
supportVectorAlphas=self.alphas[supportVectorIndex]
y_output=[]
for i in range(numSamples):
kernelValue=get_kernel_value(supportVectors,testX[i,:],self.kernel)
predict=kernelValue.T*np.multiply(supportVectorLabels,supportVectorAlphas)+self.b
if predict>=0:
y_output.append(1)
else:
y_output.append(-1)
return y_output
def test(self,test_x,test_y):
predict_y=self.predict(test_x)
numSample=len(test_x)
matchCount=0
for i in range(numSample):
if predict_y[i]==test_y[i]:
matchCount+=1
accuracy=float(matchCount/numSample)
return accuracy
def coff(self):
supportVectorsIndex = np.nonzero(self.alphas.A > 0)[0]
w=np.mat(np.zeros((2,1)))
for i in supportVectorsIndex:
w=w+np.multiply(self.alphas[i]*self.trainY[i],self.trainX[i,:].T)
return w.tolist(),self.b
def show_graph(self):
plt.scatter(self.trainX[:, 0].tolist(),self.trainX[:, 1].tolist(), c=self.trainY.tolist())
supportVectorsIndex = np.nonzero(self.alphas.A > 0)[0]
w=np.mat(np.zeros((2,1)))
for i in supportVectorsIndex:
plt.plot(self.trainX[i, 0], self.trainX[i, 1], 'og')
if self.kernel[0]=='linear':
for i in supportVectorsIndex:
w = w + np.multiply(self.alphas[i] * self.trainY[i], self.trainX[i, :].T)
min_X=min(self.trainX[:,0])[0,0]
max_X = max(self.trainX[:,0])[0,0]
min_Y = float(-self.b - w[0,0] * min_X) / w[1,0]
max_Y = float(-self.b - w[0,0] * max_X) / w[1,0]
plt.plot([min_X, max_X], [min_Y, max_Y], '-r')
plt.show()
测试代码,线性:
from SVM import SVM
from sklearn import datasets
import matplotlib.pyplot as plt
blobs=datasets.make_blobs(n_samples=100,centers=2,cluster_std=2)
X=blobs[0]
y=blobs[1]
y=[1 if i==1 or i==2 else -1 for i in y]
svm=SVM(toler=0.01,C=1,kernel_option=('linear',0))
svm.fit(X,y)
y_predict=svm.predict(X)
plt.scatter(X[:,0],X[:,1],c=y_predict)
svm.show_graph()
from SVM import SVM
from sklearn import datasets
import matplotlib.pyplot as plt
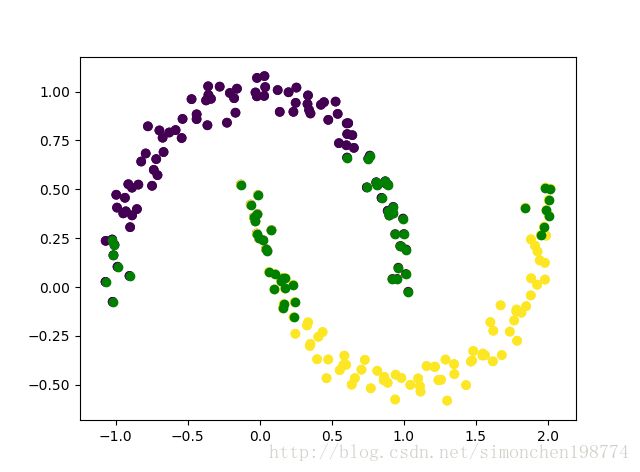
moon=datasets.make_moons(n_samples=200, noise=0.05, random_state=0)
X=moon[0]
y=moon[1]
y=[1 if i==1 or i==2 else -1 for i in y]
svm=SVM(toler=0.01,C=1,kernel_option=('linear',0))
svm.fit(X,y)
y_predict=svm.predict(X)
plt.scatter(X[:,0],X[:,1],c=y_predict
svm.show_graph()