leetcode回溯算法
LeetCode--回溯法心得
武汉大学 软件工程硕士在读
关注他
206 人赞同了该文章
这两天在刷LeetCode37题解数独时,被这个回溯法折腾的不要不要的,于是我疼定思疼发誓一定要找个能解决这类回溯法的套路出来,方便以后快速解决此类题目。于是我在网上找了两个很经典的回溯法题目--八皇后问题和迷宫问题,认真总结了一番,发现其中还真的有一些共同之处,我会在下面好好讲述。
首先,回溯法所用到的核心思想就是递归法,虽然其过程逻辑很清楚,而且执行效率很高。但缺点也是与之对应的,逻辑清楚,必然其抽象性很高,所以有时候就是这样的情况:看它的解题过程很容易看懂,但要是让你自己动手写这个递归过程,发现很难下笔。当时我就是这样的情况,于是我想在网上找找看看能不能有哪位大佬分享一些解题心得供我们这些算法渣渣思考学习的,然而网上的一些csdn博客(这儿不是刻意贬低csdn的哈)写的东西都是千篇一律,都是在把一些旧的不能再旧的东西炒来炒去,没有一点营养!别人靠不住,那就只能靠自己呗!于是我自己找例子,自己琢磨,终于是有些小收获,本着慈悲为怀的精神,故想拿出来供大家参考,避免大家少趟坑,保证不打马虎眼,不炒现饭。当然了,若有不当之处,请各位笔友指出,面的误人子弟。
1 八皇后问题
问题描述:
该问题是国际西洋棋棋手马克斯·贝瑟尔于1848年提出:在8×8格的国际象棋上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法。
看完问题描述后,大家之前要是熟悉此题目的也可以先动手做做,看看还能不能解出来。再正式回答此题目之前我还是先把我写的答案贴出来,让大家对整个处理过程有个大致的印象。
八皇后问题代码如下:
# 检测皇后之间的位置关系
def conflict(queen_str, current_queen):
"""
:param queen_str: str-->指代当前皇后存放之前的所有皇后的集合
:param current_queen: int-->指代当前皇后想要存放的位置
:return:Flag: boolean-->指代当前位置的皇后是否与之前所有位置的皇后有冲突
"""
# 此处的queen_length既是之前保存的queen_list集合的长度,也可以理解为当前current_queen皇后的行下标
queen_length = len(queen_str)
# 定义是否有位置冲突的标签
Flag = False
for index in range(queen_length):
# queen_length - index主要是控制相邻两行的皇后不能处于对角线上,其他的就没要求
if abs(current_queen-int(queen_str[index])) in(0, queen_length-index):
Flag = True
break
return Flag
# 定义执行皇后问题的主函数
def queens(nums=8, queen_str=""):
"""
:param nums: int-->指代整个棋盘中想要存放皇后的个数
:param queen_str: str-->指代当前皇后存放之前的所有皇后的集合
:return:final_queens: List[int]-->指代最后符合要求的皇后的位置
"""
final_queens = []
# 定义递归函数,获取所有八皇后的值
def back(queen_str):
# 出口条件
if len(queen_str) == nums:
final_queens.append(queen_str)
return
for index in range(nums):
Flag = conflict(queen_str, index)
# 如果当前位置的皇后是否与之前所有位置的皇后没有冲突,则执行下述代码
if Flag is False:
back(queen_str+str(index))
back(queen_str)
return final_queens
if __name__ == "__main__":
final_queens = queens()
print(final_queens)
print(len(final_queens))写的应该还是比较清楚的,大家也可以再看看官方给的回溯法的描述
描述:
回溯法(探索与回溯法)是一种选优搜索法,又称为试探法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。
其实我总结起来就3点:
1 出口。一个递归算法一定要有出口,否则就是一个死循环了。出口语句一般都挺好写的,但 是出口语句该放在哪儿了,这个就是关键了,这儿容许我先卖个关子。
2 递归函数的参数。一般情况下,递归函数是要带参数的,因为递归操作都是用来处理下一次的过程,如果没有参数的话,那么就很难从下一次的操作回溯到当前操作了。这么说,可能会有点迷糊,别急,后面我会举例子,这儿还是卖个关子。
3 递归函数的处理过程。这个自不必多说,重中之重,需要好好理解其过程
上面3点就是我总结的关于回溯法的关键点了,我觉得只要真正的把这3步吃透,一般的回溯法题目是ok的(这可不是我吹牛哈)下面我就这3点仔细讲讲,大家可要竖起耳朵通清楚了哈。
1 出口
关于这个出口条件,就像我上面说的,它的关键是出口语句放置的位置,因为这个语句其实挺好写的,一般也就2-3行代码,大多数人都能想出来。但我觉得大多数人苦恼的就是不知道该把它放在哪儿,我刚开始也是这样,后面总结了2-3题之后,我发现了一个万能规律,就是把出口语句放在递归函数的第一行就行,大家可以看看八皇后问题的递归函数back()以及迷宫问题的递归函数back(),我这儿就直接贴出来。
八皇后问题的递归函数back()
# 定义递归函数,获取所有八皇后的值
def back(queen_str):
# 出口条件
if len(queen_str) == nums:
final_queens.append(queen_str)
return
for index in range(nums):
Flag = conflict(queen_str, index)
# 如果当前位置的皇后是否与之前所有位置的皇后没有冲突,则执行下述代码
if Flag is False:
back(queen_str+str(index))迷宫问题的递归函数back()
def back(position=start, pos_list=[start]):
# 该递归函数的出口
if position == final_position:
route.append(pos_list)
print("successful")
return
pos_x = position[0]
pos_y = position[1]
for direction in walk_route:
next_position = [pos_x+direction[0], pos_y+direction[1]]
if isValid(nums, next_position):
# 记住,这儿一定要用另一个list集合保存当前路线pos_list以及该路线下一个位置,方便回溯找到pos_list
# 如果直接对pos_list添加next_position,则不能回溯找到之前的pos_list
pos_list_copy = []
pos_list_copy.extend(pos_list)
pos_list_copy.append(next_position)
nums[pos_x, pos_y] = 0
back(next_position, pos_list_copy)
# 如果没有找到出口,则将当前上一个位置0重置为1,回溯
nums[pos_x, pos_y] = 1大家一对比就很清楚的看到,出口语句都是写在最前面的,其实最主要的就是不能把出口语句放在for和while循环语句里面,因为出口语句一定要方便整个函数退出,大家听不懂的强行记住没问题的,要是出了问题,也别来找我,啊哈哈哈哈哈。
2 递归函数的参数
这个递归函数的参数的设置也是有很大门道的,设置的好就很容易得到答案,否则弄大半天可能还是没有一点反应。大家一定要记住一点:这个参数是随着每一次的递归操作而发生改变的。而回溯法很关键的一点就是:如果当前操作行不通,如何回溯到上一步操作。大家继续看上面贴的两个递归函数的参数,会发现其参数都是要改变的,既然参数会发生改变,那么我们要如何保存其上一步操作的值呢?大家可以再细细看看上述两个函数的传值操作。
八皇后问题的传值操作
for index in range(nums):
Flag = conflict(queen_str, index)
# 如果当前位置的皇后是否与之前所有位置的皇后没有冲突,则执行下述代码
if Flag is False:
back(queen_str+str(index))大家可以看到back(queen_str+str(index))这一步,其传的参数就是queen_str+str(index) 其实想法就是不破坏当前参数的值,直接把当前值加上一个值(大家可以理解为定义了另一个非queen_str当前值的值给传到下一次函数),只要不破坏当前值,函数就能回溯。这一步很关键,大家可以好好品味。
for index in range(nums):
Flag = conflict(queen_str, index)
# 如果当前位置的皇后是否与之前所有位置的皇后没有冲突,则执行下述代码
if Flag is False:
queen_str = queen_str+str(index)
back(queen_str )如果大家还有些疑惑的话,可以再把传值操作改成这样试试,你会发现结果会大相径庭的,这里就是破坏了当前值。
迷宫问题的传值操作
if isValid(nums, next_position):
# 记住,这儿一定要用另一个list集合保存当前路线pos_list以及该路线下一个位置,方便回溯找到pos_list
# 如果直接对pos_list添加next_position,则不能回溯找到之前的pos_list
pos_list_copy = []
pos_list_copy.extend(pos_list)
pos_list_copy.append(next_position)
nums[pos_x, pos_y] = 0
back(next_position, pos_list_copy)
# 如果没有找到出口,则将当前上一个位置0重置为1,回溯
nums[pos_x, pos_y] = 1大家再可以参考迷宫操作的传值操作理解。
关于参数,我还有一点就是强调:就是结果一定是要有一个全局参数来保存,这个全局参数不会随着每一次的递归操作而随时改变,它只是用来保存每一次递归操作成功时的结果,其它的不关它的事。你仔细看看这两个程序也会发现:它们在一开始就定义了一个List空列表。大家也可以照搬的,凡是结果需要保存的题目90%以上就是要预先定义一个List空列表(不要问我这个90%数据是怎么得来的哈,问了我也不知道,哈哈哈哈哈)
八皇后问题的List空列表
# 定义执行皇后问题的主函数
def queens(nums=8, queen_str=""):
"""
:param nums: int-->指代整个棋盘中想要存放皇后的个数
:param queen_str: str-->指代当前皇后存放之前的所有皇后的集合
:return:final_queens: List[int]-->指代最后符合要求的皇后的位置
"""
# 定义一个保存结果的List列表
final_queens = []迷宫问题的List空列表
"""
迷宫问题,使用回溯法
"""
def maze(nums, start):
"""
:param nums: List[List[int]]-->指代所给的迷宫
:param start: List[int X, Y]-->指代起始点位置
:return: route: List[]
"""
# 定义最终路线的集合
route = []3 递归函数的处理过程
这个过程是最关键的了,但是也很少有人能把它说清楚,当然也包括我。我想来想去,总结起来一句话就是:如果当前递归过程的处理参数符合要求,则执行相关赋值或其它操作,然后转入下一次递归,如果下一次递归不能找到出口,则把之前相关赋值或其它操作重置为初始状态。说的有些抽象,但我目前确实是说的这么样了,还需要自己好好看几个题目,好好做几道题目才能理解这层意思。大家也可以好好看看下述迷宫问题的处理过程。
迷宫问题的处理过程
nums[pos_x, pos_y] = 0
back(next_position, pos_list_copy)
# 如果没有找到出口,则将当前上一个位置0重置为1,回溯
nums[pos_x, pos_y] = 12 迷宫问题
问题描述:
定义一个二维数组:
int maze[5][5] = {
0, 1, 0, 0, 0,
0, 1, 0, 1, 0,
0, 0, 0, 0, 0,
0, 1, 1, 1, 0,
0, 0, 0, 1, 0,
};
它表示一个迷宫,其中的1表示墙壁,0表示可以走的路,只能横着走或竖着走,不能斜着走,要求编程序找出从左上角到右下角的最短路线。
解题思路:
本题我才用的方法也是很常规的广度优先搜索(BFS)也就是定义四个方向,即上下左右,对迷宫内每个可以通过的点执行该四个方向的操作。具体的操作我这儿就不说了,直接贴代码吧!
迷宫问题代码如下:
mport numpy as np
# 检查当前位置是否有效
# 如果当前位置为0,则表示不能通过;
# 如果当前位置表示为1,则表示可以继续通过
def isValid(nums, current_position):
'''
:param nums: List[List[int]]-->指代所给的迷宫
:param current_position: List[int X, Y]-->指代当前坐标点位置
:return: boolean-->指代当前位置是否有效
'''
pos_x = current_position[0]
pos_y = current_position[1]
if pos_x in range(len(nums)) and pos_y in range(len(nums)) and nums[pos_x, pos_y] == 1:
return True
else:
return False
"""
迷宫问题,使用回溯法
"""
def maze(nums, start):
"""
:param nums: List[List[int]]-->指代所给的迷宫
:param start: List[int X, Y]-->指代起始点位置
:return: route: List[]
"""
# 定义最终路线的集合
route = []
# 定义当前点上下左右移动方向的集合
walk_route = [[-1, 0], [0, -1], [1, 0], [0, 1]]
# 获取迷宫的终点
nums_length = len(nums)
final_position = [nums_length-1, nums_length-1]
def back(position=start, pos_list=[start]):
# 该递归函数的出口
if position == final_position:
route.append(pos_list)
print("successful")
return
pos_x = position[0]
pos_y = position[1]
for direction in walk_route:
next_position = [pos_x+direction[0], pos_y+direction[1]]
if isValid(nums, next_position):
# 记住,这儿一定要用另一个list集合保存当前路线pos_list以及该路线下一个位置,方便回溯找到pos_list
# 如果直接对pos_list添加next_position,则不能回溯找到之前的pos_list
pos_list_copy = []
pos_list_copy.extend(pos_list)
pos_list_copy.append(next_position)
nums[pos_x, pos_y] = 0
back(next_position, pos_list_copy)
# 如果没有找到出口,则将当前上一个位置0重置为1,回溯
nums[pos_x, pos_y] = 1
back()
return route
if __name__ == "__main__":
nums = [[1, 0, 0, 1, 0, 1], [1, 1, 1, 0, 1, 0], [0, 0, 1, 0, 1, 0], [0, 1, 1, 1, 0, 0], [0, 0, 0, 1, 1, 1],
[1, 0, 0, 0, 1, 1]]
nums = np.array(nums)
print(nums)
current_position = [0, 0]
print(maze(nums, current_position))该讲的我在八皇后问题那儿都讲到了,本题大家就用作检验方法和思考作用吧。
3 解数独
问题描述
编写一个程序,通过已填充的空格来解决数独问题。
一个数独的解法需遵循如下规则:
- 数字
1-9在每一行只能出现一次。 - 数字
1-9在每一列只能出现一次。 - 数字
1-9在每一个以粗实线分隔的3x3宫内只能出现一次。
空白格用 '.' 表示。
一个数独。
答案被标成红色。
Note:
- 给定的数独序列只包含数字 1-9 和字符 '.' 。
- 你可以假设给定的数独只有唯一解。
- 给定数独永远是 9x9 形式的。
思路:
这一题是LeetCode上面的第37题,确实是挺恶心的,当时做了两三天。但如果你把它解答出来了,我觉得你对应回溯法的理解应该是差不多了。下面我还是直接贴代码了,相关注解我都在代码里写的很清楚了,大家应该很容易看得懂!
代码如下:
import numpy as np
class Solution(object):
# 本题采用回溯法解决
# 当时在area3x3检查时栽了跟头
def solveSudoku(self, board):
"""
:type board: List[List[str]]
:rtype: void Do not return anything, modify board in-place instead.
"""
# board = np.array(board)
def back(board, position=[0, 0]):
# 如果当前数独中没有空白元素'.',则说明查找成功了
if position == [-1, -1]:
print("successful")
return True
# 获取当前位置的横纵坐标
pos_x = position[0]
pos_y = position[1]
# 获取当前位置的值
pos_value = board[pos_x][pos_y]
if pos_value == '.':
for index in range(1, 10):
value = str(index)
if self.isValid(board, position, value) is True:
board[pos_x][pos_y] = value
next_position = self.getNextPosition(board, position)
if back(board, next_position) is True:
return True
else:
board[pos_x][pos_y] = '.'
else:
next_pos = self.getNextPosition(board, position)
back(board, next_pos)
return False
back(board)
return board
# 获取下一个有效点的坐标位置
def getNextPosition(self, board, position):
next_x = position[0]
next_y = position[1]
while board[next_x][next_y] != '.':
next_y += 1
if next_y >= len(board):
next_x += 1
next_y = 0
if next_x not in range(len(board)) or next_y not in range(len(board)):
return [-1, -1]
return [next_x, next_y]
# 判断当前位置是否有效
def isValid(self, board, position, value):
"""
:param board: array[[]]-->指代所给的数独列表
:param position: List[int x, y]-->指代所给的当前位置
:param value: str-->指代当前位置的值
:return: boolean-->若返回为True,则表示当前位置有效;反之,则无效
"""
board = np.array(board)
# 获取当前位置的横纵坐标
pos_x = position[0]
pos_y = position[1]
# 获取当前位置横纵坐标所对应的每一行每一列元素
pos_row = board[pos_x]
pos_col = board[:, pos_y]
# 如果当前位置的值value与其所在的每一行或者每一列的值重复,则表示当前值无效,返回False
if value in pos_row or value in pos_col:
return False
# 获取当前位置点所在的3x3区域的位置
area3x3_x = pos_x//3*3
area3x3_y = pos_y//3*3
area3x3_batch = board[area3x3_x:area3x3_x+3, area3x3_y:area3x3_y+3]
# 如果当前位置的值value与其所在的3x3区域的值重复,则表示当前值无效,返回False
if value in area3x3_batch:
return False
return True
if __name__ == "__main__":
board = [['5', '3', '.', '.', '7', '.', '.', '.', '.'],
['6', '.', '.', '1', '9', '5', '.', '.', '.'],
['.', '9', '8', '.', '.', '.', '.', '6', '.'],
['8', '.', '.', '.', '6', '.', '.', '.', '3'],
['4', '.', '.', '8', '.', '3', '.', '.', '1'],
['7', '.', '.', '.', '2', '.', '.', '.', '6'],
['.', '6', '.', '.', '.', '.', '2', '8', '.'],
['.', '.', '.', '4', '1', '9', '.', '.', '5'],
['.', '.', '.', '.', '8', '.', '.', '7', '9']]
result = Solution().solveSudoku(board)
print(np.array(result))暂时就补充这么多了,如果有更好的想法,我也会及时补充的,当然了,各位读者如果有更nice的解题套路也希望大家积极分享!!!
2019/3/19 19:13补充
昨天有位朋友给我出了道题,也是涉及回溯法的,我觉得很有意思,所以想分享出来。
题目如下:
思路:
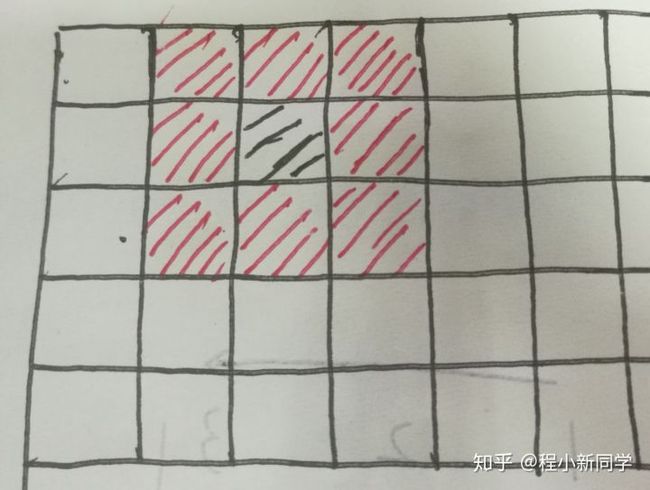
因为这个方格是不规则的方格,所以我首先想到的是将它填充成一个规则方格,便于我们插值。 如图所示:
之所以这样,是因为我们就可以直接对每个方格内的元素的相邻方格内元素作比较了。
如图所示:
编辑于 2019-03-19