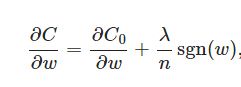深度学习中的trick

下面浅谈深度学习中的技巧。

学习率（learning rate）

学习率的设置应该随着迭代次数的增加而减小，每迭代完指定次epoch也就是对整个数据过一遍，然后对学习率进行变化，这样能够保证每个样本得到公平的对待。

卷积神经网络CNN中的技巧

CNN中将一个大尺寸的卷积核分解成多层的小尺寸的卷积核或者分解成多层的一维卷积，这样能够减少参数并增加非线性。

CNN中的网络设计应该逐渐减少图像尺寸，同时增加通道数，让空间信息转化为高阶抽象的特征信息。

数据扩充（Data Augmentation）

数据扩充，又名数据增强。其目的是在缺少海量数据时，为了保证模型的有效训练，从原始数据中生成更多的数据出来。

数据扩充方法包括：

1、翻转包括水平翻转、垂直翻转、水平垂直翻转。

2、旋转是常取的角度为-30、-15、15、30度等。

3、尺度变换是指将图像分辨率变为原图的0.8、1.1、1.2倍等，生成新图。

4、抠取包括随机抠取和监督式抠取。随机抠取在原图的随机位置抠取图像块作为新图像；监督式抠取只抠取含有明显语义信息的图像块。

5、色彩抖动是对原有的像素值分布进行轻微扰动，即加入轻微的噪声作为新图像。

6、Fancy PCA对所有训练数据的像素值进行主成分分析，根据得到的特征值和特征向量计算一组随机值，作为扰动加入到原来像素值中。

预训练

预训练模型（pre-trained model）是前人为了解决某个问题所创造出来的问题。在解决新的问题时，不需要从零开始训练一个新模型，可以从类似问题中训练过的模型入手，在原有模型的基础上进行微调继续训练。该方法不仅在时间上或者准确率上都有较好的效果。

权重初始化（weight initialization）

深度学习中权重初始化对模型收敛速度和模型质量有着重要的影响。参数在刚开始不能全都初始化为0，因为如果所有的参数都是0，那么所有神经元的输出都将是相同的，在反向传播时同一层内所有的神经元的行为也都一致。

激活函数

激活函数的主要作用是提供网络的非线性建模能力。如果没有激活函数，那么不管网络有多少层都仅能够表达线性映射。激活函数应具有如下性质：

1、可微性：当优化方法是基于梯度的时候，这个性质是必须的；

2、单调性：当激活函数是单调函数的时候，单层网络能够保证是凸函数；

3、输出值的范围：当激活函数输出值是有限的时候，基于梯度的优化方法会更加稳定。

常见的激活函数介绍：

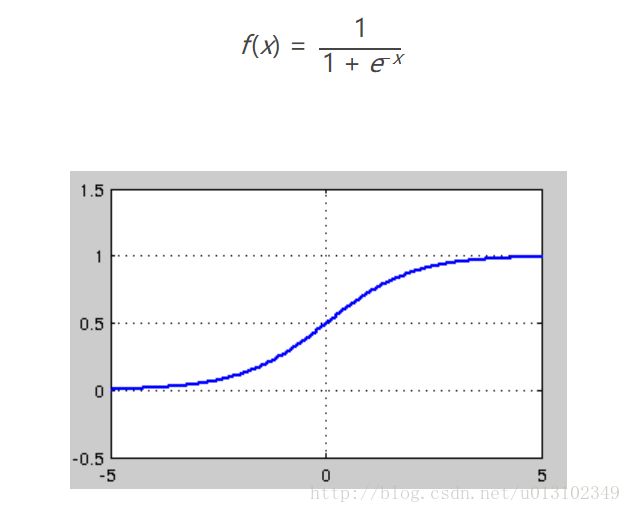
sigmoid函数

sigmoid缺陷是有明显的饱和性，从上图可以看出，其两侧的导数逐渐趋近于0.在反向传播的过程中，sigmoid向下传导的梯度包含导数因子，一旦输入落入饱和区，导数会接近于0，导致梯度在传递过程中越来越小，因此网络很难得到有效地训练，这种现象被称为梯度消失。

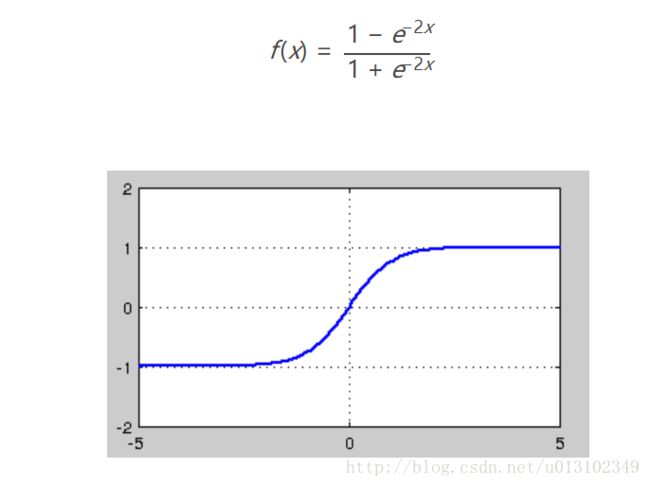
tanh

tanh激活函数输出的均值为0，收敛速度比sigmoid快，从而减少了迭代次数，训练更快。但是从图中可以看出，tanh激活函数同样有饱和性，从而噪声梯度消失。

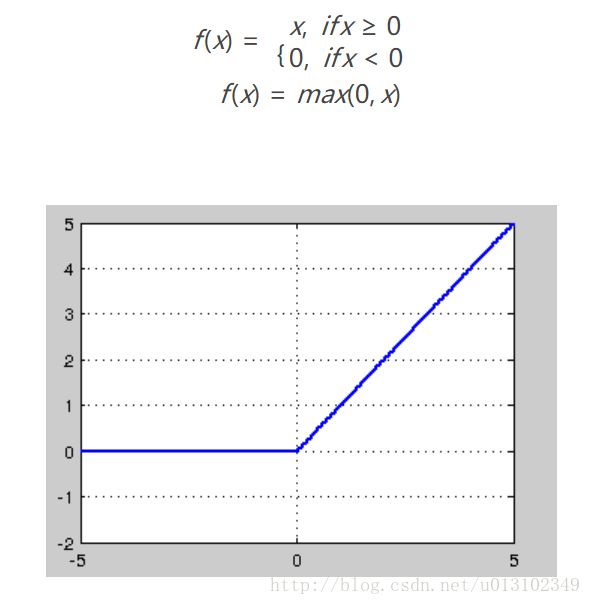
ReLU

ReLU的全称是Rectified Linear Units。当x<0时，ReLU硬饱和;当x>0时，不存在饱和的问题。ReLU能够保持在x>0时梯度不衰减，从而缓解了梯度消失的问题。

但是随着训练的推进，部分输入会落入硬饱和区，导致对应权重无法更新。这种现象被称为“神经元死亡”。与sigmoid类似，ReLU的输出均值也大于0，偏移现象和 神经元死亡会共同影响网络的收敛性。

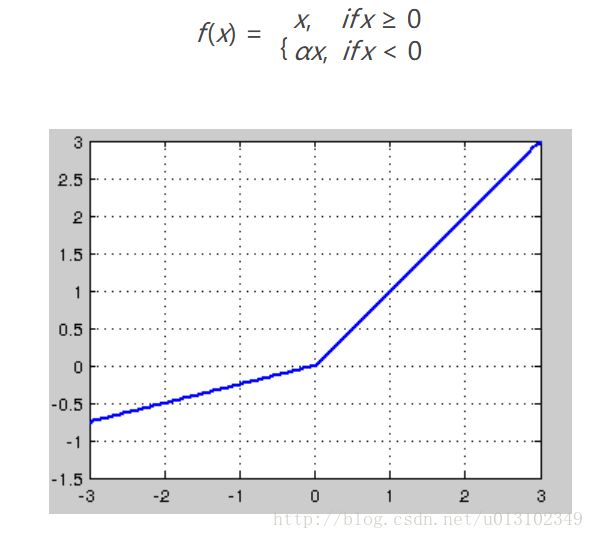
Leaky-ReLU

针对在x<0的硬饱和问题，对ReLU做出相应的改进:

 

ELU

融合了sigmoid和ReLU，左侧具有软饱和性，右侧无饱和性。右侧线性部分使得ELU能够缓解梯度消失，而左侧软饱能够让ELU对输入变化或噪声更鲁棒。ELU的输出均值接近于零，所以收敛速度更快。在 ImageNet上，不加 Batch Normalization 30 层以上的 ReLU 网络会无法收敛，PReLU网络在MSRA的Fan-in （caffe ）初始化下会发散，而 ELU 网络在Fan-in/Fan-out下都能收敛。

Maxout

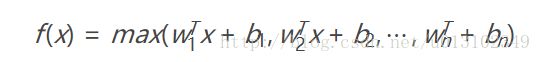
maxout网络能够近似任意连续函数，且当w2,b2,…,wn,bn为0时，退化为ReLU。Maxout能够缓解梯度消失，同时又规避了ReLU神经元死亡的缺点，但增加了参数和计算量。

正则化（regularization）

避免过拟合的方法之一是增加训练数据数量，或者减小网络的规模。但是往往大型的网络比小型网络有更大的潜力。在使用固定的网络和固定的训练数据进行网络训练时，为了避免过拟合，提高模型的泛化能力，可以采用正则化的方法。

如上图所示，随着训练过程的进行，模型复杂度增加，在训练数据上错误逐渐减小，但是在验证集上的错误率反而逐渐增大，这是因为模型出现了过拟合的现象，对训练集外的数据准确率较低。

L2  regularization(权重衰减)

L2正则化是在代价函数后面加上一个正则化项：

C0是原始的代价函数，后面一项为L2正则化项，即所有参数w的平方和除以训练集的样本大小n。λ是正则项系数，权衡正则项和原始代价函数C0的比重，1/2是为了求导方便。

推导过程：

先求导：

可以发现L2正则化项对b的更新没有影响，但是对w的更新有影响：

在不使用L2正则化时，w前的系数为1，现在w前面系数为 1−ηλ/n ，因为η、λ、n都是正的，所以 1−ηλ/n小于1，它的效果是减小w，这也就是权重衰减（weight decay）的由来。当然考虑到后面的导数项，w最终的值可能增大也可能减小。

另外，需要提一下，对于基于mini-batch的随机梯度下降，w和b更新的公式跟上面给出的有点不同：

对比上面w的更新公式，可以发现后面那一项变了，变成所有导数加和，乘以η再除以m，m是一个mini-batch中样本的个数。

更小的权值w，从某种意义上说，表示网络的复杂度更低，对数据的拟合刚刚好（这个法则也叫做奥卡姆剃刀）。

过拟合的时候，拟合函数的系数往往非常大。过拟合，就是拟合函数需要顾忌每一个点，最终形成的拟合函数波动很大。在某些很小的区间里，函数值的变化很剧烈。这就意味着函数在某些小区间里的导数值（绝对值）非常大，由于自变量值可大可小，所以只有系数足够大，才能保证导数值很大。而正则化是通过约束参数的范数使其不要太大，所以可以在一定程度上减少过拟合情况。

L1 regularization

在原始的代价函数后面加上一个L1正则化项，即所有权重w的绝对值的和，乘以λ/n.

求导:

上式中sgn(w)表示w的符号。那么权重w的更新规则为：

比原始的更新规则多出了η * λ * sgn(w)/n这一项。当w为正时，更新后的w变小。当w为负时，更新后的w变大——因此它的效果就是让w往0靠，使网络中的权重尽可能为0，也就相当于减小了网络复杂度，防止过拟合。

参考：

[1] http://blog.csdn.net/u012162613/article/details/44261657