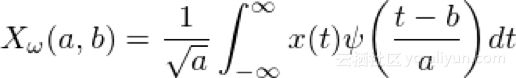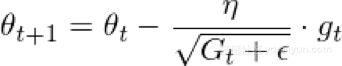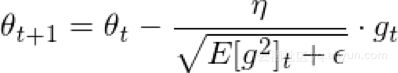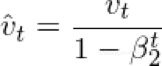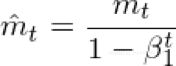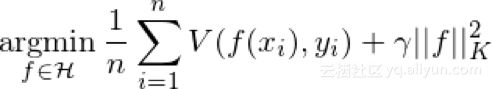使用机器学习来预测股票价格

机器学习和深度学习已经在金融机构中找到了自己的位置，因为它们能够以高精度预测时间序列数据，并且工程师们仍在继续研究以使模型更好。这篇文章是我使用机器学习来预测股票价格的入门项目。

它基于我的项目AlphaAI，这是一个堆叠的神经网络架构，可以预测各个公司的股票价格。该项目是2018年iNTUtion的决赛项目之一。

工作流程

该项目的工作流程基本上是以下步骤：

1.获取股票价格数据；

2.使用小波变换去噪数据；

3.使用Stacked Autoencoders提取特征；

4.使用特征训练LSTM；

5.测试预测准确性的模型；

在这篇文章中，我将详细介绍每个步骤以及为什么做出某些决定。

1.数据采集

pandas_datareader是借助雅虎财经的API，它可以很容易获得股票价格数据，只需使用以下命令即可完成：

stock_data = pdr.get_data_yahoo(self.ticker, self.start, self.end)

2.数据去噪

由于股票市场动态的复杂性，股票价格数据通常充满了可能分散机器学习算法分散趋势和结构的噪声。因此，删除一些噪声是符合我们的诉求，同时也可以保留数据中的趋势和结构。起初，我想使用傅里叶变换（不熟悉的人应该阅读这篇文章），但我认为小波变换可能是保留数据时间因素的更好选择，而不是仅产生基于频率的输出。

小波变换

小波变换与傅立叶变换密切相关，只是用于变换的函数是不同的，并且这种变换发生的方式也略有不同。

过程如下：

1.使用小波变换来变换数据；

2.消除超过完全标准偏差的系数（在所有系数中）；

3.反变换新系数以获得去噪数据；

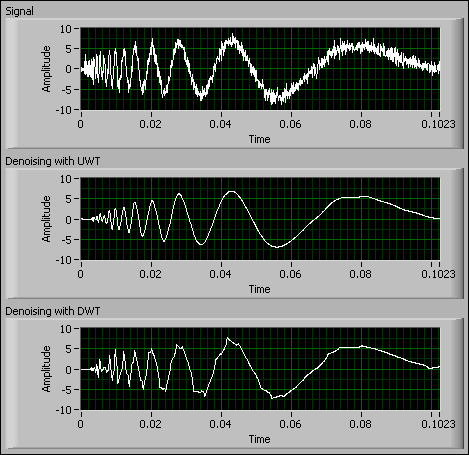
以下是小波变换如何对时间序列数据进行去噪的示例：

如你所见，在去噪版本中不存在初始信号中存在的随机噪声，这正是我们要查看的股票价格数据。

这是去噪数据的代码：

x = np.array(self.stock_data.iloc[i: i + 11, j])                
(ca, cd) = pywt.dwt(x, "haar")                
cat = pywt.threshold(ca, np.std(ca), mode="soft")                
cdt = pywt.threshold(cd, np.std(cd), mode="soft")                
tx = pywt.idwt(cat, cdt, "haar")

该库pywt非常适合小波变换，这也极大地减轻了我的负担。

3.提取特征

在大多数机器学习环境中，提取特征需要专家领域知识，这是我没有的奢侈品。我或许可以尝试使用某种形式的技术指标，如平均线或平均收敛差异（MACD）或动量指标，但我觉得盲目地使用它可能不是最优的。

但是，通过使用堆叠自动编码器或其他机器学习算法（如受限的Boltzmann机器），可以实现自动特征提取。由于编码的可解释性与限制Boltzmann机器的概率相比，我选择使用堆叠自动编码器。

堆叠式自动编码器

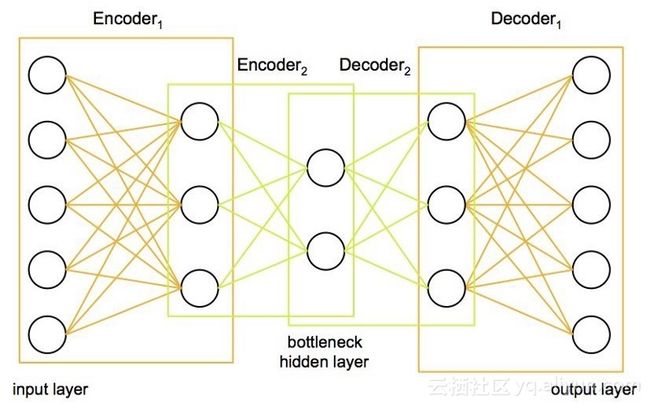
从本质上讲，堆叠式自动编码器非常适合压缩数据并再次复制数据。我们感兴趣的是压缩部分，因为它意味着重现数据所需的信息以某种方式以压缩形式编码。这表明这些压缩数据在某种程度上可能是我们试图从中提取特征的数据的特征。以下是堆叠自动编码器的网络结构：

输入数据被压缩成所需的许多神经元，并且网络被迫使用自动编码器重建初始数据。这会强制模型提取数据的关键元素，我们可以将其解释为要素。需要注意的一点是，由于没有输入输出对，这个模型实际上属于无监督学习，但输入和输出其实都是相同的。

我们可以使用keras构建这样的模型。

class AutoEncoder:
    def __init__(self, encoding_dim):
        self.encoding_dim = encoding_dim
def build_train_model(self, input_shape, encoded1_shape, encoded2_shape, decoded1_shape, decoded2_shape):
        input_data = Input(shape=(1, input_shape))
encoded1 = Dense(encoded1_shape, activation="relu", activity_regularizer=regularizers.l2(0))(input_data)
        encoded2 = Dense(encoded2_shape, activation="relu", activity_regularizer=regularizers.l2(0))(encoded1)
        encoded3 = Dense(self.encoding_dim, activation="relu", activity_regularizer=regularizers.l2(0))(encoded2)
        decoded1 = Dense(decoded1_shape, activation="relu", activity_regularizer=regularizers.l2(0))(encoded3)
        decoded2 = Dense(decoded2_shape, activation="relu", activity_regularizer=regularizers.l2(0))(decoded1)
        decoded = Dense(input_shape, activation="sigmoid", activity_regularizer=regularizers.l2(0))(decoded2)
autoencoder = Model(inputs=input_data, outputs=decoded)
encoder = Model(input_data, encoded3)
# Now train the model using data we already preprocessed
        autoencoder.compile(loss="mean_squared_error", optimizer="adam")
train = pd.read_csv("preprocessing/rbm_train.csv", index_col=0)
        ntrain = np.array(train)
        train_data = np.reshape(ntrain, (len(ntrain), 1, input_shape))
# print(train_data)
        # autoencoder.summary()
        autoencoder.fit(train_data, train_data, epochs=1000)

我使用从2000年到2008年的去噪股票价格数据训练了自动编码器。经过1000个epoch的训练后，RMSE降至0.9左右。然后，我使用该模型将剩余的股票价格数据编码为特征。

4. LSTM模型

LSTM模型不需要介绍，因为它在预测时间序列中变得非常普遍和流行。它从细胞状态的存在中获得了卓越的预测能力，使其能够理解和学习数据的长期趋势。这对我们的股票价格数据尤为重要,下面我将讨论我认为重要的设计选择的某些方面。

优化器

所使用的优化器类型可以极大地影响算法收敛到最小值的速度。此外，重要的是存在一些随机性概念，以避免陷入局部最小值且未达到全局最小值。这其中有一些很棒的算法，但我选择使用Adam优化器。Adam优化器成功的结合了另外两个优化器的优势：ADAgrad和RMSprop。

ADAgrad优化器基本上对每个参数和每个时间步使用不同的学习速率。ADAgrad背后的问题是：不常见的参数必须具有较大的学习率，而频繁的参数必须具有较小的学习率。换句话说，ADAgrad的随机梯度下降更新成为：

，其中。

基于已经为每个参数计算的过去梯度来计算学习速率。因此，

其中G是过去梯度平方和的矩阵，这种优化的问题是随着迭代次数的增加，学习率开始迅速消失。

RMSprop考虑通过仅使用一定数量的先前梯度来固定递减的学习速率。更新成为

其中 

既然我们已经理解了这两个优化器是如何工作的，那么我们可以研究一下Adam的工作方式。

自适应矩估计（Adam）是另一种通过考虑过去平方梯度的指数衰减平均值来计算每个参数的自适应学习率的方法。这可以表示为

   

v和m可以分别被认为是梯度的第一和第二时刻的估计，因此得到自适应矩估计的名称。当这是第一次使用时，研究人员观察到存在0的固有偏差，他们通过使用以下估计来反驳这一点：

    

这导致我们进入最终的梯度更新规则

这是我使用的优化器，其好处总结如下：

1.  每个参数和每次迭代的学习率都不同；

2.  与ADAgrad一样，学习并没有减少；

3.  梯度更新使用权重分布矩阵。

正则化

训练模型的另一个重要方面是确保权重不会太大并关注一个数据点，或者称为过度拟合。所以我们应该对大权重设置惩罚（大的程度取决于所使用的常规者的类型）。我选择使用Tikhonov正则化，可以将其视为以下最小化问题：

函数空间在再生核Hilbert空间（RKHS）中确保了规范的概念存在。这允许我们将规范的概念编码到我们的正则化器中。

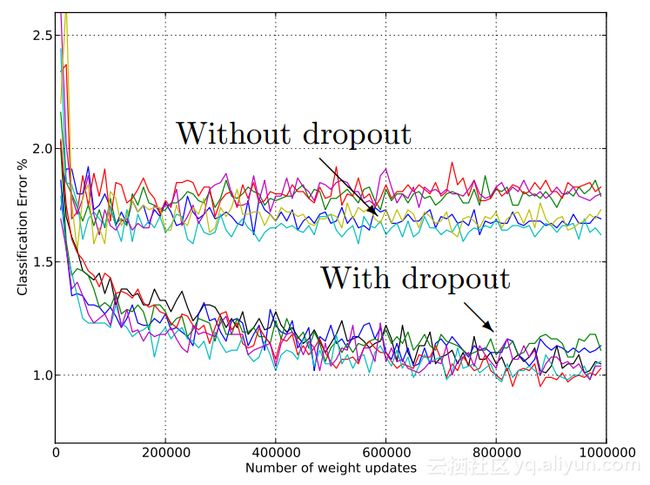
Dropout

一种新的防止过度拟合的方法,具体用在当一些神经元突然不起作用时会发生什么。这迫使模型不要过度依赖任何神经元组，而是考虑所有这些神经元。dropout已经发现它们可以使神经元更加健壮，从而使它们能够预测趋势，而无需关注任何一个神经元。以下是使用dropout的结果：

5.模型实施

上述所有分析都可以在keras及其功能API轻松地实现。这是模型的代码（查看整个代码，查看我的GitHub：AlphaAI）

class NeuralNetwork:
    def __init__(self, input_shape, stock_or_return):
        self.input_shape = input_shape
        self.stock_or_return = stock_or_return
def make_train_model(self):
        input_data = kl.Input(shape=(1, self.input_shape))
        lstm = kl.LSTM(5, input_shape=(1, self.input_shape), return_sequences=True, activity_regularizer=regularizers.l2(0.003),
                       recurrent_regularizer=regularizers.l2(0), dropout=0.2, recurrent_dropout=0.2)(input_data)
        perc = kl.Dense(5, activation="sigmoid", activity_regularizer=regularizers.l2(0.005))(lstm)
        lstm2 = kl.LSTM(2, activity_regularizer=regularizers.l2(0.01), recurrent_regularizer=regularizers.l2(0.001),
                        dropout=0.2, recurrent_dropout=0.2)(perc)
        out = kl.Dense(1, activation="sigmoid", activity_regularizer=regularizers.l2(0.001))(lstm2)
model = Model(input_data, out)
        model.compile(optimizer="adam", loss="mean_squared_error", metrics=["mse"])
# load data
train = np.reshape(np.array(pd.read_csv("features/autoencoded_train_data.csv", index_col=0)),
                           (len(np.array(pd.read_csv("features/autoencoded_train_data.csv"))), 1, self.input_shape))
        train_y = np.array(pd.read_csv("features/autoencoded_train_y.csv", index_col=0))
        # train_stock = np.array(pd.read_csv("train_stock.csv"))
# train model
model.fit(train, train_y, epochs=2000)

结果

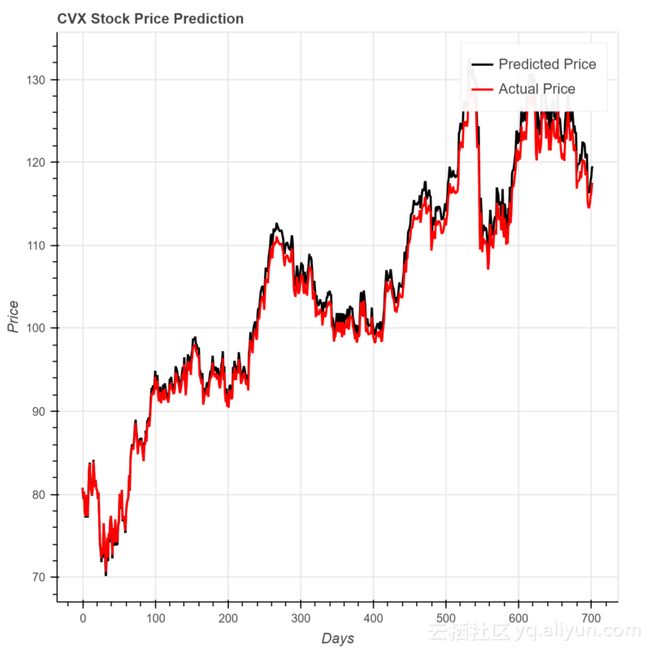
这些是我对各公司的预测结果。

对于雪佛龙来说，MSE是2.11

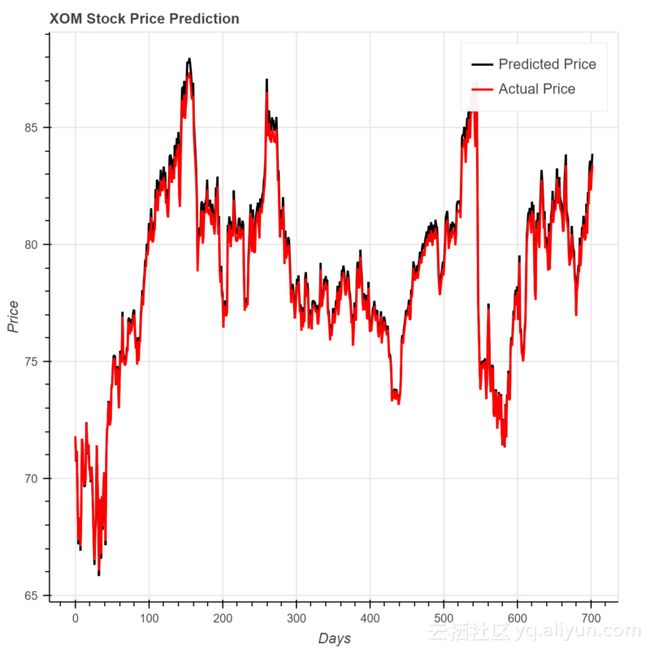
对于埃克森美孚，MSE为0.0945

很明显，使用这种神经网络架构的结果令人印象深刻，并且如果实施到策略中可以是有利可图的。

在线学习

除了从历史数据中学习模型之外，我还想让模型实时学习，甚至从预测中学习。因此，我已经使它成为一个学习和预测的在线模型。换句话说，它可以学习历史数据，预测明天的价格，另外当实际价格已知时，它也会学习使用它。所以模型总是在改进。

除了使用实际价格来改善之外，我还考虑制作一个二级模型，该模型使用关于公司的新闻和Twitter的情绪值。我将首先概述如何获取这些数据。

Twitter数据

除了股票价格数据，我还想尝试一些自然语言处理。因此，我尝试深入研究使用来自Twitter和新闻的情绪数据来改进股票预测。

第一个斗争就是免费获取推文，因为获取整个实时数据的Twitter API已经被禁止。但是，我找到了一个允许我在过去10天内获取推文的API，然后我可以实现某种形式的NLP来从推文中提取情绪数据。这不是最佳的，但对我的在线学习模型仍然有用。

新闻数据

与Twitter类似，获取新闻数据非常困难。我尝试分析彭博文章的网址，但实现从2000年手动报废网站几乎是不可能的。因此，我选择了具有相当强大的抓取模型的Aylien API。

这些新闻文章被删除的条件是他们只包括股票和财经新闻，过滤到前150个Alexa网站，并且使用指数加权移动平均线平均情绪分数，以考虑最近的新闻而不是旧的新闻。

在线模型

鉴于我的情绪分数，我使用额外的神经网络层来更正我的预测误差。但是，在本文发布时，结果不可用，因为生成一个数据点需要一天的时间。

结论

神经网络非常善于预测时间序列数据，当与情感数据结合时，可以真正建立一个实用的模型。虽然这里的结果令人印象深刻，但我仍然想方设法改进它，也许实际上可以从中制定完整的交易策略。目前，我正在研究使用强化学习来开发一个使用预测模型结果的交易代理。

本文由阿里云云栖社区组织翻译。

文章原标题《using-machine-learning-to-predict-stock-prices》

作者：Vivek Palaniappan 译者：虎说八道，审校：。

文章为简译，更为详细的内容，请查看原文。