决策树(分类树、回归树）

决策树

前言：第一篇博客，最近看完决策树，想着归纳一下，也方便自己以后回顾。写的会比较全面一些，可能会有很多不太正确的地方，欢迎大家交流指正 : )

---

决策树模型：

决策树模型是运用于分类以及回归的一种树结构。决策树由节点和有向边组成，一般一棵决策树包含一个根节点、若干内部节点和若干叶节点。决策树的决策过程需要从决策树的根节点开始，待测数据与决策树中的特征节点进行比较，并按照比较结果选择选择下一比较分支，直到叶子节点作为最终的决策结果。

• 内部节点：对应于一个属性测试
• 叶节点：对应于决策结果
• 根节点包含样本全集；
• 每个节点包括的样本集合根据属性测试的结果被划分到子节点中；
• 根节点到每个叶节点的路径对应对应了一个判定测试路径；

决策树的结构还是比较好理解的，如果不明白，可以看一下图中的例子，这是一个简单判断这个键盘我喜不喜欢的决策树模型：

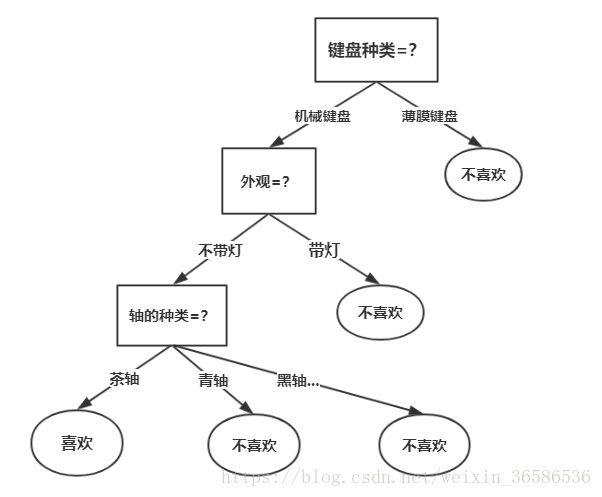
目标变量可以采用一组离散值的树模型称为分类树(常用的分类树算法有ID3、C4.5、CART)，而目标变量可以采用连续值（通常是实数）的决策树被称为回归树(如CART算法)。

决策树算法本质上就是要找出每一列的最佳划分以及不同列划分的先后顺序及排布

---

决策树学习算法：

• 特征选择
• 决策树生成
• 决策树剪枝

(下面讨论的都是分类树，回归树会在后面单独再谈)

特征选择：

特征选择也即选择最优划分属性，从当前数据的特征中选择一个特征作为当前节点的划分标准。我们希望在不断划分的过程中，决策树的分支节点所包含的样本尽可能属于同一类，即节点的“纯度”越来越高。而选择最优划分特征的标准不同，也导致了决策树算法的不同。

为了找到最优的划分特征，我们需要先了解一些信息论的知识：

• 信息熵(information entropy)
• 信息增益(information gain)
• 信息增益率(information gain ratio)
• 基尼指数(Gini index)

熵：
在信息论和概率统计中，熵(entropy)是表示随机变量不确定性的度量，设X是一个取有限值的离散随机变量，其概率分布为

P(X=xi)=pi,i=1,2,...,n P ( X = x i ) = p i , i = 1 , 2 , . . . , n

则随机变量 X X 的熵定义为

H(X)=−∑i=1npilogpi H ( X ) = − ∑ i = 1 n p i l o g p i

上述公式中的对数通常以2为底
熵越大，随机变量的不确定性越大。为了能够更好地理解熵的意义，我们下面举一个例子来说明。
当随机变量只取两个值，如1，0时，即 X X 的分布为

P(X=1)=p,P(X=0)=1−p,0≤p≤1 P ( X = 1 ) = p , P ( X = 0 ) = 1 − p , 0 ≤ p ≤ 1

则熵为

H(p)=−plog2p−(1−p)log2(1−p) H ( p ) = − p l o g 2 p − ( 1 − p ) l o g 2 ( 1 − p )

H(p) H ( p ) 的函数图像如下：

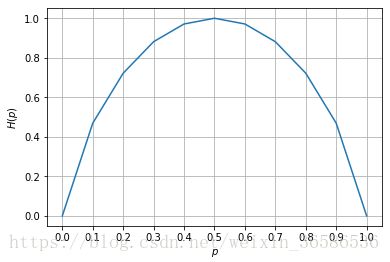
从图中我们不难看出 p=0or1 p = 0 o r 1 时 H(p) H ( p ) 为0，即不确定性为0。当 p=0.5 p = 0.5 时，不确定性最大。

条件熵：
设有随机变量 (X,Y) ( X , Y ) 。条件熵 H(Y|X) H ( Y | X ) 表示在已知随机变量 X X 的条件下随机变量 Y Y 的不确定性。随机变量 X X 给定的条件下随机变量 Y Y 的条件熵 H(Y|X) H ( Y | X ) 定义为 X X 给定条件下 Y Y 的条件概率分布的熵对 X X 的数学期望

H(Y|X)=∑i=1npiH(Y|X=xi) H ( Y | X ) = ∑ i = 1 n p i H ( Y | X = x i )

这里， pi=P(X=xi),i=1,2,...,n p i = P ( X = x i ) , i = 1 , 2 , . . . , n

信息增益：
信息增益表示得知特征 X X 的信息而使得类 Y Y 的信息的不确定性减少程度。接下来给出定义，特征 A A 对训练数据集 D D 的信息增益 g(D,A) g ( D , A ) ,为集合 D D 的熵 H(D) H ( D ) 与特征 A A 给定条件下 D D 的条件熵 H(D|A) H ( D | A ) 之差，即

g(D,A)=H(D)−H(D|A) g ( D , A ) = H ( D ) − H ( D | A )

• 信息增益的算法:

  输入：训练数据集 D D ，特征 A A
  输出：特征 A A 对训练数据集 D D 的信息增益 g(D,A) g ( D , A )
  (1): ( 1 ) : 计算数据集 D D 的熵 H(D) H ( D )
  

  H(D)=−∑k=1K|Ck||D|log2|Ck||D| H ( D ) = − ∑ k = 1 K | C k | | D | l o g 2 | C k | | D |
  
  (2): ( 2 ) : 计算特征 A A 对训练数据集 D D 的条件熵 H(D|A) H ( D | A )
  
  H(D|A)=∑i=1n|Di||D|H(Di)=−∑i=1n|Di||D|∑k=1K|Dik||Di|log2|Dik||Di| H ( D | A ) = ∑ i = 1 n | D i | | D | H ( D i ) = − ∑ i = 1 n | D i | | D | ∑ k = 1 K | D i k | | D i | l o g 2 | D i k | | D i |
  
  (3): ( 3 ) : 计算信息增益
  
  g(D,A)=H(D)−H(D|A) g ( D , A ) = H ( D ) − H ( D | A )
  
  |D| | D | 为样本容量，设有 K K 个类 Ck,k=1,2,...,K,|Ck| C k , k = 1 , 2 , . . . , K , | C k | 为属于类 Ck C k 的样本个数。设特征 A A 有 n n 个不同取值，根据特征 A A 的取值将 D D 划分为 n n 个子集 D1,D2,...,Dn D 1 , D 2 , . . . , D n , Dik D i k 为子集 Di D i 中属于类 Ck C k 的集合。

信息增益率：
特征 A A 对训练数据集 D D 的信息增益 gR(D,A) g R ( D , A ) 定义为其信息增益 g(D,A) g ( D , A ) 与训练数据集 D D 关于特征 A A 的值的熵 HA(D) H A ( D ) 之比，即

gR(D,A)=g(D,A)HA(D) g R ( D , A ) = g ( D , A ) H A ( D )

其中， HA(D)=−∑ni=1|Di||D|log2|Di||D|,n H A ( D ) = − ∑ i = 1 n | D i | | D | l o g 2 | D i | | D | , n 是特征 A A 取值的个数。
注意区别 H(D|A) H ( D | A ) 和 HA(D) H A ( D )

基尼指数：
基尼指数 Gini(D) G i n i ( D ) 表示集合 D D 不确定性，基尼指数 Gini(D，A=a) G i n i ( D ， A = a ) 表示集合 D D 经 A=a A = a 分割后的不确定性(类似于熵)，基尼指数越小，样本的不确定性越小。
分类问题中，假设有 K K 个类，样本点属于第 k k 类的概率为 pk, p k , 则概率分布的基尼指数定义为

Gini(p)=∑k=1Kpk(1−pk)=1−∑k=1Kp2k G i n i ( p ) = ∑ k = 1 K p k ( 1 − p k ) = 1 − ∑ k = 1 K p k 2

如果样本集合 D D 根据特征 A A 是否取某一可能值 a a 被分割成 D1 D 1 和 D2 D 2 两部分，即
D1= D 1 = { (x,y)∈D|A(x)=a ( x , y ) ∈ D | A ( x ) = a } ,D2=D−D1 , D 2 = D − D 1
则在特征 A A 的条件下,集合 D D 的基尼指数定义为

Gini(D,A=a)=|D1||D|Gini(D1)+|D2||D|Gini(D2) G i n i ( D , A = a ) = | D 1 | | D | G i n i ( D 1 ) + | D 2 | | D | G i n i ( D 2 )

---

决策树生成

生成算法	划分标准
ID3 I D 3	信息增益
C4.5 C 4.5	信息增益率
CART C A R T	基尼指数

ID3: I D 3 :

ID3 I D 3 算法的核心是在决策树各个节点上根据信息增益来选择进行划分的特征，然后递归地构建决策树。
具体方法：

1. 从根节点开始，对节点计算所有可能的特征的信息增益，选择信息增益值最大的特征作为节点的划分特征；
2. 由该特征的不同取值建立子节点；
3. 再对子节点递归地调用以上方法，构建决策树；
4. 到所有特征的信息增益都很小或者没有特征可以选择为止，得到最终的决策树

ID3 I D 3 的局限：

1. 没有剪枝
2. 采用信息增益作为选择最优划分特征的标准，然而信息增益会偏向那些取值较多的特征(这也是 C4.5 C 4.5 采用信息增益率的原因)

C4.5: C 4.5 :

C4.5 C 4.5 与 ID3 I D 3 相似，但对 ID3 I D 3 进行了改进，在这里不再详细描述 C4.5 C 4.5 的实现，就讲一下有哪些基于 ID3 I D 3 的改进：

1. 用信息增益率来选择划分特征，克服了用信息增益选择的不足
2. 在构造树的过程中进行剪枝
3. 可对连续值与缺失值进行处理

为什么 C4.5 C 4.5 要用信息增益率代替信息增益？为什么信息增益会偏向多取值特征？

信息增益在面对类别较少的离散数据时效果较好，但是面对取值较多的特征时效果会很不如人意。关于信息增益对取值较多特征的偏向性，我认为原因是：当特征的取值较多时，根据此特征划分得到的子集纯度有更大的可能性会更高(对比与取值较少的特征)，因此划分之后的熵更低，由于划分前的熵是一定的，因此信息增益更大，因此信息增益比较偏向取值较多的特征。举个较为极端的例子可能更好理解：如果特征 A A 的取值能将每一个样本都分到一个节点当中去的时候(如编号等特征)，条件熵部分会为0，这意味着该情况下的信息增益达到了最大值，故ID3算法一定会选择特征A。但是，显然的，我们知道这个特征A显然不是最佳选择。
那么为什么信息增益率就能改善这种情况呢？先来看一下信息增益率的计算公式：

gR(D,A)=g(D,A)HA(D) g R ( D , A ) = g ( D , A ) H A ( D )

其中， HA(D)=−∑ni=1|Di||D|log2|Di||D| H A ( D ) = − ∑ i = 1 n | D i | | D | l o g 2 | D i | | D | , HA(D) H A ( D ) 又叫做特征 A A 的内部信息， HA(D) H A ( D ) 其实像是一个衡量以特征 A A 的不同取值将数据集 D D 分类后的不确定性的度量。如果特征 A A 的取值越多，那么不确定性通常会更大，那么 HA(D) H A ( D ) 的值也会越大，而 1HA(D) 1 H A ( D ) 的值也会越小。这相当于是在信息增益的基础上乘上了一个惩罚系数。即 gR(D,A)=g(D,A)∗ g R ( D , A ) = g ( D , A ) ∗ 惩罚系数.
(我的理解如果有什么错误的地方的话，希望大家能够指正，不胜感激XD)

CART: C A R T :

CART(classificationandregressiontree), C A R T ( c l a s s i f i c a t i o n a n d r e g r e s s i o n t r e e ) , 分类回归树算法，既可用于分类也可用于回归，在这一部分我们先主要将其分类树的生成。区别于 ID3 I D 3 和 C4.5 C 4.5 , CART C A R T 假设决策树是二叉树，内部节点特征的取值为“是”和“否”，左分支为取值为“是”的分支，右分支为取值为”否“的分支。这样的决策树等价于递归地二分每个特征，将输入空间(即特征空间)划分为有限个单元。 CART C A R T 的分类树用基尼指数来选择最优特征的最优划分点，具体过程如下

1. 从根节点开始，对节点计算现有特征的基尼指数，对每一个特征，例如 A A ，再对其每个可能的取值如 a a ,根据样本点对 A=a A = a 的结果的”是“与”否“划分为两个部分，利用 Gini(D,A=a)=|D1||D|Gini(D1)+|D2||D|Gini(D2) G i n i ( D , A = a ) = | D 1 | | D | G i n i ( D 1 ) + | D 2 | | D | G i n i ( D 2 ) 进行计算；
2. 在所有可能的特征 A A 以及该特征所有的可能取值 a a 中，选择基尼指数最小的特征及其对应的取值作为最优特征和最优切分点。然后根据最优特征和最优切分点，将本节点的数据集二分，生成两个子节点
3. 对两个字节点递归地调用上述步骤，直至节点中的样本个数小于阈值，或者样本集的基尼指数小于阈值，或者没有更多特征后停止；
4. 生成 CART C A R T 分类树；

回归树：

回归树是可以用于回归的决策树模型，一个回归树对应着输入空间（即特征空间）的一个划分以及在划分单元上的输出值.与分类树不同的是，回归树对输入空间的划分采用一种启发式的方法，会遍历所有输入变量，找到最优的切分变量 j j 和最优的切分点 s s ，即选择第 j j 个特征 xj x j 和它的取值 s s 将输入空间划分为两部分，然后重复这个操作。
而如何找到最优的 j j 和 s s 是通过比较不同的划分的误差来得到的。一个输入空间的划分的误差是用真实值和划分区域的预测值的最小二乘来衡量的，即

∑xi∈Rm(yi−f(xi))2 ∑ x i ∈ R m ( y i − f ( x i ) ) 2

其中， f(xi) f ( x i ) 是每个划分单元的预测值，这个预测值是该单元内每个样本点的值的均值，即

f(xi)=cm=ave(yi|xi∈Rm) f ( x i ) = c m = a v e ( y i | x i ∈ R m )

(将输入空间划分为 M M 个单元 R1,R2,...,Rm R 1 , R 2 , . . . , R m )

那么， j j 和 s s 的求解可以用下式进行

minj,s[minc1∑xi∈R1(j,s)(yi−c1)2+minc2∑xi∈R2(j,s)(yi−c2)2] m i n j , s [ m i n c 1 ∑ x i ∈ R 1 ( j , s ) ( y i − c 1 ) 2 + m i n c 2 ∑ x i ∈ R 2 ( j , s ) ( y i − c 2 ) 2 ]

其中， R1(j,s)= R 1 ( j , s ) = { x|xj≤s x | x j ≤ s }和 R2(j,s)= R 2 ( j , s ) = { x|xj>s x | x j > s }是被划分后的两个区域

梳理一下上述内容，最小二乘回归树的生成方法如下

1. 选择最优的切分变量 j j 和最优的切分点 s s ，求解
   
   minj,s[minc1∑xi∈R1(j,s)(yi−c1)2+minc2∑xi∈R2(j,s)(yi−c2)2] m i n j , s [ m i n c 1 ∑ x i ∈ R 1 ( j , s ) ( y i − c 1 ) 2 + m i n c 2 ∑ x i ∈ R 2 ( j , s ) ( y i − c 2 ) 2 ]
   
   遍历所有特征，对固定的特征扫描所有取值，找到使上式达到最小值的对 (j,s) ( j , s ) .
2. 用选定的对 (j,s) ( j , s ) 划分区域，并确定该区域的预测值；
3. 继续对两个字区域调用上述步骤，直至满足停止条件；
4. 生成回归树；

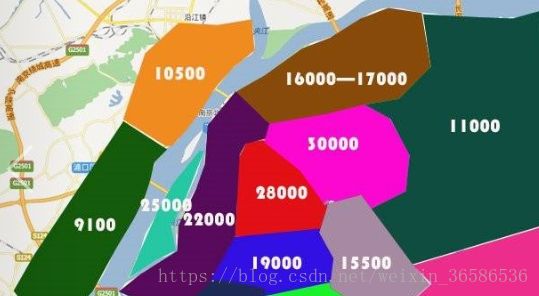
举个例子，我们要对南京市各地区的房价进行回归预测，我们将输入空间不断的按最小误差进行划分，得到类似下图的结果，将空间划分后，我们会用该单元内的均值作为该单元的预测值，如图中一片区域的平均房价作为该划分单元内房价的预测值(唔，怎么感觉这个例子还是不太准确…）。

(图片来源于网络，如有侵权会马上删除：)

---

决策树剪枝

准备写的时候才发现我自己剪枝这部分并没有搞得非常清楚，只能先放在这，日后再进行更新好了。。。

---

参考文献

[1] 李航. 统计学习方法[M]. 北京：清华大学出版社，2012