图分类《Hierarchical Graph Representation Learning with Differentiable Pooling》阅读笔记

图分类《Hierarchical Graph Representation Learning with Differentiable Pooling》阅读笔记

Abstract

对于graph neural networks (GNNs)，大体上分三种任务：Node Classification，Link Prediction和 Graph Classification。本文关注的是Graph Classification。作者提到，现有的GNN本质上是flat的，而没有学习到hierarchical的图表达。原文描述如下：

‘’However, current GNN methods are inherently flat and do not learn hierarchical representations of graphs—a limitation that is especially problematic for the task of graph classification, where the goal is to predict the label associated with an entire graph.‘’

为此，作者提出了DIFFPOOL，一种能够学习到图的层次表达并可以结合多种端到端的GNNs结构可微的图池化模块。DIFFPOOL为每一层的nodes学习可微的软聚类(soft cluster assignment)， 将nodes映射到一组簇中，这一组簇将作为下一层GNN Layer的输入(coarsened input)。

Introduction

问题分析

对于flat的不足和hierarchical的必要性，作者描述为：flat的本质是聚合信息只能通过edges完成而不能以hierarchical的方式推断和聚合信息。原文描述如下：

“A major limitation of current GNN architectures is that they are inherently flat as they
only propagate information across the edges of the graph and are unable to infer and aggregate the information in a hierarchical way.”

标准的方法首先为所有nodes学习embeddings，然后通过globally pool聚合所有的node embeddings。比如用简单的simple summation或者作用在整个集合上的神经网络。作者列举了四篇采用此类标准方法的文章：

[1] http://proceedings.mlr.press/v48/daib16.pdf

[2] https://papers.nips.cc/paper/5954-convolutional-networks-on-graphs-for-learning-molecular-fingerprints.pdf

[3] https://arxiv.org/pdf/1704.01212.pdf

[4] https://arxiv.org/pdf/1511.05493.pdf

关于此类标准方法的limitations，作者还是强调hierarchical结构更适用于Graph Classification任务。

作者所提方法类似于CNNs中的空间池化(Spatial Pooling Operation)。难点在于，gragh结构没有空间局部性(notion of spatial locality)，也就是说难以直接地将nodes池化到一起，因为graph的拓扑结构不能直接构建"patch"。并且不同的graphs中nodes和edges的数量也不同。

解决方案

聚类nodes来构建一个在低层图(underlying graph)上面的分层次的多层结构(hierarchical multi-layer scaffold)。DIFFPOOL在GNN每一层学习一个soft assignment，使nodes映射为簇集合。然后通过stacking GNN layers构建分层结构(hierarchical fashion)。

上图所展示的对DIFFPOOL的High-level的说明：在每一个hierarchical layer，首先用一个GNN Layer学习nodes的embeddings，然后用学习到的embeddings对nodes进行cluster得到coarsened graph，接着用另一个GNN Layer学习coarsened graph。

Proposed Method

首先是Graph的Notation：

GNNs的"Message-Passing"结构：

H为node embeddings,即“Messages”。M为message propagation函数。DIFFPOOL方法对M不敏感，也就是适用于各种M。

给定GNN Layer的输出Z = GNN(A,X)，邻接矩阵A。该方法要学习一个新的coarsened graph (m < n)，A’ (nxn), Z’ (mxd)。然后coarsened graph作为其他GNN Layer的输入。迭代K次，如上面的框架图所示。现在要解决的问题是，如果利用Z来cluster或pool本层的nodes，从而能够让coarsened graph作为下一层的输入，而且这种方法要适用于各种M和每个Layer。

如何获取coarsened graph

定义第l层的Cluster Assignment Matrix：

S每行表示l层的一个node(cluster)，每一列表示l+1层的一个node(cluster)。作者称之为一种***soft assignment***。这里看代码比较好理解。

在奥格找法师开了个传送门：https://github.com/EstelleHuang666/gnn_hierarchical_pooling

DIFFPOOL定义如下：

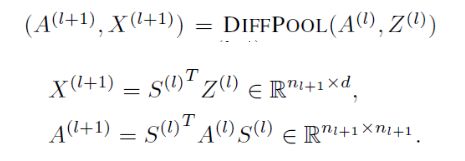
A为实矩阵，表示全连接的加权图(a fully connected edge-weighted graph)。A_ij表示cluster i与cluster j的连接强度(Connectivity Strength)。X中的第i行表示cluster i的embedding。Coarsened adjacency matrix A和Cluster embeddings X将作为另一个GNN Layer的输入。

如何获取assignment matrix S和embedding matrices Z

作者通过同样以cluster node features X 和 coarsened adjacency matrix A为输入的两个独立的GNN Layer分别生成S和Z。生成Z的GNN就是标准的GNN模块，命名为embedding GNN：

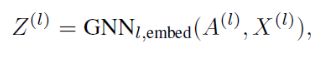
生成S的GNN为加了softmax的GNN Layer：

这里的softmax是row-wise fashion的。从矩阵乘法的角度去看这个公式：

相当于*(l+1, l) x (l, d) = (l+1, d)*，也就是基于多个权重的对nodes在每一维特征上的加权聚合。这里的多个权重，我理解为作者所提到的hierarchical。关于每一层中cluster数量的设置为超参，最后cluster数量为1用于获取最终的graph embedding vector。

关于优化

关于优化，是用梯度下降法完成的。但作者提到在训练过程中对下式的优化困难。

所以这里应用了auxiliary link prediction objective，使临界节点能够被pool在一起。在每一层，作者通过下式优化：

作者提到的关于Pooling GNN另一个重要的性质是每个node的cluster assignment的输出应该倾向于one-hot的形式，从而使cluster之间的关系更加清晰。所以作者提出通过优化下式来达到上述目的：

最后每层的L_LP和L_E和分类损失相加。作者提到加了这两个损失函数会使收敛变慢，但效果更好。

Conclusion

精巧的艺术品，向优秀的作者致敬

除了复杂度略大

才疏学浅，欢迎批评

慢慢来比较快

有个公众号是我和好朋友一起玩的，欢迎来一起交流