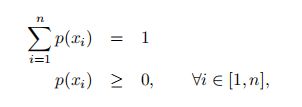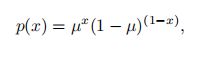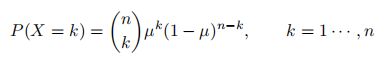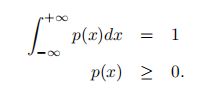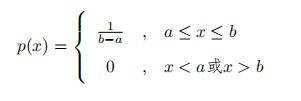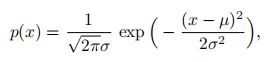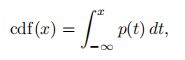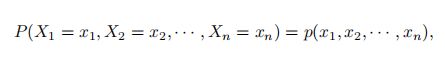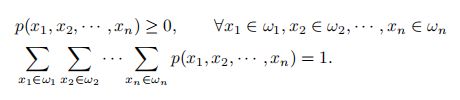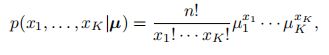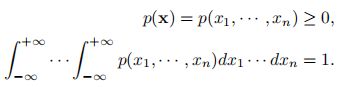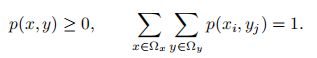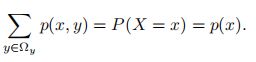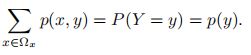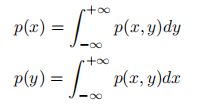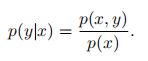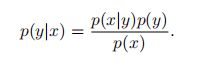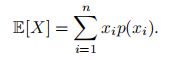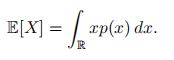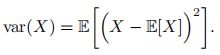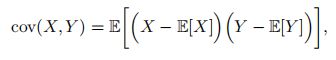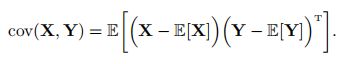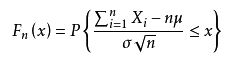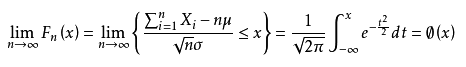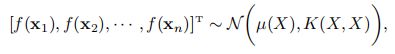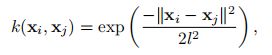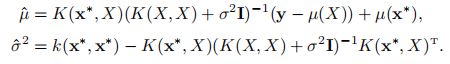前言 机器学习中的数学归纳整理（概率论部分）
本文收录归纳了一些机器学习中涉及到概率论的部分，主要用于研究建模究大量随机现象中的数量规律。
目录
1事件和概率
1.1 随机变量
1.1.1 离散随机变量
1.1.2 连续随机变量
1.1.3 累积分布函数
1.2 随机向量
1.2.1 离散随机向量
1.2.2 连续随机向量
1.2.3 边际分布
1.2.4 条件概率分布
1.2.5 独立与条件独立
1.2.6 期望和方差
1.2.7 Jensen 不等式
1.2.8 大数定律
1.2.9 中心极限定理
2 随机过程
2.1 马尔可夫过程
2.1.1 马尔可夫链
2.2 高斯过程
1事件和概率
1.1 随机变量
在随机试验中，试验的结果可以用一个数 X 来表示，这个数 X 是随着试验结果的不同而变化的，是样本点的一个函数。我们把这种数称为随机变量。例如，随机掷一个骰子，得到的点数就可以看成一个随机变量X，X 的取值为{1, 2, 3, 4, 5, 6}。如果随机掷两个骰子，整个事件空间Ω可以由36个元素组成：Ω = {(i, j)|i = 1, . . . , 6; j = 1, . . . , 6}
一个随机事件也可以定义多个随机变量。比如在掷两个骰子的随机事件中，可以定义随机变量X 为获得的两个骰子的点数和，也可以定义随机变量Y 为获得的两个骰子的点数差。随机变量X 可以有11个整数值，而随机变量Y 只有6个。
X(i, j) := i + j, x = 2, 3, . . . , 12
Y (i, j) := | i − j |, y = 0, 1, 2, 3, 4, 5.
其中i, j 分别为两个骰子的点数。
1.1.1 离散随机变量
如果随机变量X 所可能取的值为有限可列举的，有n个有限取值{x1, · · · , xn},则称X 为离散随机变量。
要了解X 的统计规律，就必须知道它取每种可能值xi 的概率，即P(X = xi) = p(xi), ∀i ∈ [1, n].
p(x1), · · · , p(xn)称为离散型随机变量X 的概率分布或分布，并且满足：
伯努利分布 在一次试验中，事件A出现的概率为µ，不出现的概率为1 − µ。若用变量X 表示事件A出现的次数，则X 的取值为0和1，其相应的分布为：
二项分布 在n 次伯努利分布中，若以变量 X 表示事件 A出现的次数，则 X 的取值为{0, · · · , n}，其相应的分布为二项分布：
其中
为二项式系数（这就是二项分布的名称的由来），表示从n个元素中取出k 个元素而不考虑其顺序的组合的总数。
1.1.2 连续随机变量
与离散随机变量不同，一些随机变量X 的取值是不可列举的，由全部实数或者由一部分区间组成，比如：
X = {x|a ≤ x ≤ b}, −∞ < a < b < ∞
则称X 为连续随机变量。连续随机变量的值是不可数及无穷尽的。
连续随机变量X 的概率分布一般用概率密度函数p(x)来描述。p(x)为可积函数，并满足：
给定概率密度函数p(x)，便可以计算出随机变量落入某一个区间的概率，而p(x)本身反映了随机变量取落入x的非常小的邻近区间中的概率大小。
常见的连续随机变量的概率分布有：
均匀分布 若a, b为有限数，[a, b]上的均匀分布的概率密度函数定义为：
正态分布 正态分布又名高斯分布，是自然界最常见的一种分布，并且具有很多良好的性质，在很多领域都有非常重要的影响力，其概率密度函数为：
其中，σ > 0，µ和σ 均为常数。若随机变量X 服从一个参数为µ和σ 的概率分布，简记为：
当µ = 0，σ = 1时，称为标准正态分布。
1.1.3 累积分布函数
对于一个随机变量X，其累积分布函数是随机变量X 的取值小于等于x的概率。
以连续随机变量X 为例，累积分布函数定义为：
其中p(x)为概率密度函数。下图给出了标准正态分布和累计分布函数。
1.2 随机向量
随机向量是指一组随机变量构成的向量。如果X1, X2, · · · , Xn 为n个随机变量, 那么称 [X1, X2, · · · , Xn] 为一个 n 维随机向量。一维随机向量称为随机变量。随机向量也分为离散随机向量和连续随机向量。
1.2.1 离散随机向量
离散随机向量的联合概率分布为：
其中xi ∈ ωi 为变量Xi 的取值，ωi 为变量Xi 的样本空间。
和离散随机变量类似，离散随机向量的概率分布满足：
多项分布 一个常见的离散向量概率分布为多项分布。多项分布是二项分布在随机向量的推广。假设一个袋子中装了很多球，总共有K 个不同的颜色。我们从袋子中取出n个球。每次取出一个球时，就在袋子中放入一个同样颜色的球。这样保证同一颜色的球在不同试验中被取出的概率是相等的。令X为一个K 维随机向量，每个元素Xk(k = 1, · · · , K)为取出的n个球中颜色为k 的球的数量，则X 服从多项分布，其概率分布为：
其中![\mu = [\mu _1, ... , \mu _K]^T](http://img.e-com-net.com/image/info8/158c01716eb647268685de41c3bc7df1.gif){kind=small}
分别为每次抽取的球的颜色为1,..., K 的概率；x1, ... , xK为非负整数，并且满足：
多项分布的概率分布也可以用gamma函数表示：
其中
为 gamma 函数。这种表示形式和 Dirichlet 分布类似，而Dirichlet分布可以作为多项分布的共轭先验。
1.2.2 连续随机向量
连续随机向量的其联合概率密度函数满足：
多元正态分布 一个常见的连续随机向量分布为多元正态分布，也称为多元高斯分布。若n维随机向量X = [X1, . . . , Xn]
T 服从n元正态分布，其密度函数为：
其中µ为多元正态分布的均值向量，Σ为多元正态分布的协方差矩阵，|Σ|表示Σ的行列式。
各项同性高斯分布 如果一个多元高斯分布的协方差矩阵简化为
，即每一个维随机变量都独立并且方差相同，那么这个多元高斯分布称为各项同性高斯分布。Dirichlet 分布 一个n维随机向量X的Dirichlet分布为：
其中α = [α1, . . . , αK]^T 为Dirichlet分布的参数。
1.2.3 边际分布
对于二维离散随机向量(X, Y )，假设X 取值空间为Ωx，Y 取值空间为Ωy。其联合概率分布满足：
对于联合概率分布p(x, y)，我们可以分别对x和y 进行求和。
（1）对于固定的x，
（2）对于固定的y，
由离散随机向量(X, Y )的联合概率分布，对Y 的所有取值进行求和得到X的概率分布；而对X 的所有取值进行求和得到Y的概率分布。这里p(x)和p(y)就称为p(x, y)的边际分布。
对于二维连续随机向量(X, Y )，其边际分布为：
一个二元正态分布的边际分布仍为正态分布。
1.2.4 条件概率分布
对于离散随机向量(X, Y )，已知X = x的条件下，随机变量Y = y 的条件概率为：
这个公式定义了随机变量Y 关于随机变量X 的条件概率分布。
对于二维连续随机向量(X, Y )，已知X = x的条件下，随机变量Y = y 的条件概率密度函数为：
同理，已知Y = y 的条件下，随机变量X = x的条件概率密度函数为：
通过公式上述两个公式，我们可以得到两个条件概率p(y|x)和p(x|y)之间的关系。
这个公式称为贝叶斯定理。
1.2.5 独立与条件独立
对于两个离散（或连续）随机变量X 和Y ，如果其联合概率（或联合概率密度函数）p(x, y)满足：
p(x, y) = p(x)p(y),
则称X 和Y 相互独立。
对于三个离散（或连续）随机变量X、Y 和Z，如果条件概率（或联合概率密度函数）p(x, y|z)满足：
p(x, y|z) = P(X = x, Y = y|Z = z) = p(x|z)p(y|z),
则称在给定变量Z 时，X 和Y 条件独立。
1.2.6 期望和方差
期望 对于离散变量X，其概率分布为p(x1), · · · , p(xn)，X 的期望或均值定义为：
对于连续随机变量X，概率密度函数为p(x)，其期望定义为：
方差 随机变量X 的方差用来定义它的概率分布的离散程度，定义为：
随机变量 X 的方差也称为它的二阶矩。
则称为 X 的根方差或标准差。
协方差 两个连续随机变量X 和Y 的协方差用来衡量两个随机变量的分布之间的总体变化性，定义为：
协方差经常也用来衡量两个随机变量之间的线性相关性。如果两个随机变量的协方差为0，那么称这两个随机变量是线性不相关。两个随机变量之间没有线性相关性，并非表示它们之间独立的，可能存在某种非线性的函数关系。反之，如果X 与Y 是统计独立的，那么它们之间的协方差一定为0。
协方差矩阵 两个m和n维的连续随机向量X和Y，它们的协方差为m × n的矩阵，定义为：
协方差矩阵cov(X, Y)的第(i, j)个元素等于随机变量Xi和Yj 的协方差。两个向量变量的协方差cov(X, Y)与cov(Y, X)互为转置关系。
如果两个随机向量的协方差矩阵为对角阵，那么称这两个随机向量是无关的。
单个随机向量X的协方差矩阵定义为：
1.2.7 Jensen 不等式
如果X 是随机变量，g 是凸函数，则：
等式当且仅当 X 是一个常数或g 是线性时成立。
1.2.8 大数定律
大数定律是指n个样本X1, · · · , Xn 是独立同分布的，即E[X1] = · · · = E[Xn] = µ，那么其均值：
收敛于期望值µ。
1.2.9 中心极限定理
设随机变量X1，X2，......Xn，......独立同分布，并且具有有限的数学期望和方差：E(Xi)=μ，D(Xi)=σ20(k=1,2....)，则对任意x，分布函数：
满足：
定理是中心极限定理最简单又最常用的一种形式，在实际工作中，只要n足够大，便可以把独立同分布的随机变量之和当作正态变量。这种方法在数理统计中用得很普遍，当处理大样本时，它是重要工具。
2 随机过程
随机过程是一组随机变量Xt 的集合，其中t属于一个索引集合T 。索引集合T 可以定义在时间域或者空间域，但一般为
时间域，以实数或正数表示。当t为实数时，随机过程为连续随机过程；当t为整数时，为离散随机过程。日常生活中的很多例子包括股票的波动、语音信号、身高的变化等都可以看作是随机过程。常见的和时间相关的随机过程模型包括贝努力过程、随机游走、马尔可夫过程等。和空间相关的随机过程通常称为随机场。比如一张二维的图片，每个像素点（变量）通过空间的位置进行索引，这些像素就组成了一个随机过程。
2.1 马尔可夫过程
马尔可夫性质 在随机过程中，马尔可夫性质是指一个随机过程在给定现在状态及所有过去状态情况下，其未来状态的条件概率分布仅依赖于当前状态。以离散随机过程为例，假设随机变量X0, X1, · · · , XT 构成一个随机过程。这些随机变量的所有可能取值的集合被称为状态空间。如果Xt+1 对于过去状态的条件概率分布仅是Xt 的一个函数，则：
其中X0:t 表示变量集合X0, X1, · · · , Xt，
为在状态空间中的状态序列。
马尔可夫性质也可以描述为给定当前状态时，将来的状态与过去状态是条件独立的。
2.1.1 马尔可夫链
离散时间的马尔可夫过程也称为马尔可夫链。如果一个马尔可夫链的条件概率：
在不同时间都是不变的，即和时间t无关，则称为时间同质的马尔可夫链。如果状态空间是有限的，T(si, sj )也可以用一个矩阵T 表示，称为状态转移矩阵，其中元素tij 表示状态si 转移到状态sj 的概率。
平稳分布 假设状态空间大小为M，向量π = [π1, · · · , πM]^T 为状态空间中的一个分布，满足0 ≤ πi ≤ 1和
。
对于状态转移矩阵为T的时间同质的马尔可夫链，如果存在一个分布π 满足：π = Tπ
即分布π就称为该马尔可夫链的平稳分布。根据特征向量的定义可知，π 为矩阵T的（归一化）的对应特征值为1的特征向量。
如果一个马尔可夫链的状态转移矩阵T满足所有状态可遍历性以及非周期性，那么对于任意一个初始状态分布π^(0)，将经过一定时间的状态转移之后，都会收敛到平稳分布，即:
2.2 高斯过程
高斯过程也是一种应用广泛的随机过程模型。假设有一组连续随机变量X0, X1, · · · , XT，如果由这组随机变量构成的任一有限集合。
都服从一个多元正态分布，那么这组随机变量为一个随机过程。高斯过程也可以定义为：如果Xt1,··· ,tn 的任一线性组合都服从一元正态分布，那么这组随机变量为一个随机过程。
高斯过程回归 高斯过程回归是利用高斯过程来对函数分布进行直接建模。和机器学习中参数化建模（比如贝叶斯线性回归）相比，高斯过程是一种非参数模型，可以拟合一个黑盒函数，也可以给出拟合结果的置信度。
假设函数f(x)服从高斯过程，且为平滑函数，即如果两个样本点x1, x2 比较接近，那么对应的f(x1), f(x2)也比较接近。两个样本点的距离可以用核函数来定义。函数f(x)的的有限采样点服从一个多元正态分布，即
其中 X = [x1, x2, · · · , xn]，µ(X) = [µ(x1), µ(x2), · · · , µ(xn)]^T 是均值向量，K(X, X) = [k(xi, xj )]_(n×n) 是协方差矩阵，k(xi, xj ) 为衡量两个输入距离的核函数。一个常用的核函数是平方指数函数:
其中l为超参数。当xi 和xj 越接近，其核函数的值越大，表明f(xi)和f(xj )越相关。
假设f(x)的一组带噪声的观测值为(xi, yi) 1 ≤ i ≤ n，其中:
为正态分布，σ 为噪声方差。
对于一个新的样本点 
满足:
其中y = [y1, y2, · · · , yn]，
。
根据上面的联合分布，f(x^∗)的后验分布满足：
其中均值µˆ 和方差σˆ 为：
从上面第一个公式可以看出，均值函数µ(x)可以近似地互相抵消。在实际应用中，一般假设均值函数为0，均值µˆ 可以将简化为：
高斯过程回归可以认为是一种有效的贝叶斯优化方法，广泛地应用于机器学习中。