用python预测疫情发展
文章目录
- 什么是传染病动力学?
- numpy和matplotlib
- 用python实现传染病模型
- SI模型
- SIS模型
- SIR模型
- SEIR模型
- 微信公众号:邯郸路220号子彬院 获取更多
什么是传染病动力学?
最近,在报道疫情的众多新闻中,相信大家也看到过一些来预测新型冠状病毒会导致感染肺炎的人数。你一定好奇,这个人数要怎么预测呢?预测人数又有什么用呢?
事实上,从学科方向来说,这类研究属于传染病动力学,就是用数学模型去描述传染病在人群中传播的规律,从而预测患病人数,进而指导政府制定措施和政策去控制传染病的传播。
这类研究最早可追溯到18世纪Daniel Bernoulli对天花的研究,而我们今天所要介绍的SIR模型是1927年Kermack与McKendrick在为了研究伦敦黑死病而提出的,是传染病动力学中最基础的模型。
介绍了传染病模型的背景信息,不知道现在你对传染病模型更有兴趣,还是执着地对python更有兴趣呢?不论哪种,这篇文章会满足你所有的好奇心。
兄弟们,火鸡们,我们开始吧!
numpy和matplotlib
首先,安装一下这节课我们需要使用的两个python包,numpy和matplotlib。
numpy-是python进行科学和矩阵运算最常用的包。
用numpy建立一维数组,存储和计算每天传染病人数的数据。
import numpy as np
import matplotlib.pyplot as plt
用matplotlib绘制传染病人数随天数变化的曲线,给出模型预测人数变化的直观认识。
好啦,下面开始用python实现传染病模型吧。
用python实现传染病模型
为了让大家能够更好地理解,我们先不直接说SIR模型,我们从最简单的开始。
SI模型
首先想象这样一个场景,一个城市有 N N N个人,假设没有人出生和死亡,忽然有一天有 I I I个人感染了病毒成为了患者,如果每天每个患者能够有效传染 λ \lambda λ个人,那么第二天患病人数是多少呢?
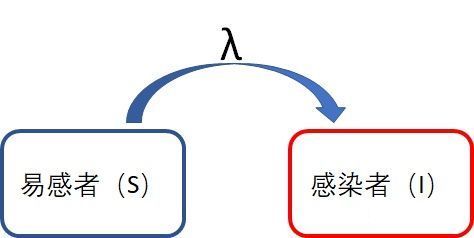
最简单的答案是: I + λ I I+\lambda I I+λI ,也就是说每天都会新增 λ I \lambda I λI个患者。那这样以来,在无限远的将来会有无穷多的人被感染,显然这是不合理的,那错在哪里?仔细思考,你一定发现了,已经患病的人就不能再被传染了,所以我们有必要把人群分为两类,易感者(S-susceptiable)和感染者(I-infective)(你猜的没错,这就是SIR中S和I的含义,R的含义之后介绍再讲)。
为了之后方便计算我们记易感者和感染者在人群中的比例为 i = I / N , s = S / N i=I/N,s=S/N i=I/N,s=S/N,那么 i + s = 1 i+s=1 i+s=1 。
我们重新考虑上面的问题,顺便来个示意图:
这样的话,每天新增的患者数为 λ × i N × s \lambda \times i N \times s λ×iN×s ,也就是总传染人数乘以易感者所占的人群比例。
那么每天的感染者比例的增加量就是 ( λ × i N × s ) / N = λ i s (\lambda \times i N \times s) / N=\lambda i s (λ×iN×s)/N=λis。
我们假设城市有一千万(N=10的7次方)人,每个患者每天接触感染每天0.8人(lamda=0.8),初始感染人数为45人(i0 = 45/N),我们来模拟70天(T=70)的情况。
# population
N = 1e7
# simuation Time / Day
T = 70
# susceptiable ratio
s = np.zeros([T])
# infective ratio
i = np.zeros([T])
# contact rate
lamda = 0.8
# initial infective people
i[0] = 45.0 / N
for t in range(T-1):
i[t + 1] = i[t] + i[t] * lamda * (1.0 - i[t])
相信其他语句大家都明白,新知识是这两行:
s = np.zeros([T])
i = np.zeros([T])
这两句话的意思是一样的,就是利用numpy(已被我们重新命名为np)的函数(zeros())来建立一个所有元素都是零的数组,而给的参数决定了这个数组的维度。比如:
a = np.zeros([2,3])
a
array([[0., 0., 0.],
[0., 0., 0.]])
a = np.zeros([5])
a
array([0., 0., 0., 0., 0.])
类似的还有产生元素全部是1的数组的函数np.ones():
a = np.ones([5])
a
array([1., 1., 1., 1., 1.])
a = np.ones([2,3])
a
array([[1., 1., 1.],
[1., 1., 1.]])
plt.plot(i)
[]
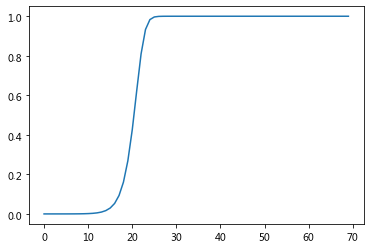
实现SI模型的核心代码是第三个cell的第11,12行:
for t in range(T-1):
i[t + 1] = i[t] + i[t] * lamda * (1.0 - i[t])
就是我们建立的数学模型,利用python的for循环语句累加迭代的方式把每天的增加量叠加到感染者比例上。
运行代码完成计算,我们利用matplotlib的pyplot来画出感染者的随天数的变化曲线:
fig, ax = plt.subplots(figsize=(8,4))
ax.plot(i, c='r', lw=2)
ax.set_xlabel('Day',fontsize=20)
ax.set_ylabel('Infective Ratio', fontsize=20)
ax.grid(1)
plt.xticks(fontsize=20)
plt.yticks(fontsize=20);
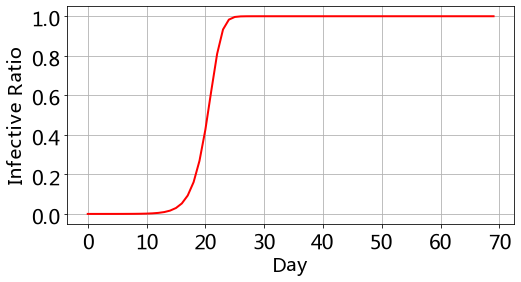
从这个结果看到,大约在25天左右,全部人群都会变成感染者,感染率 i = 1 i=1 i=1。
在程序中我们假设每天每个患者传染0.8个人,你可以改变lamda的值,观察全部人群感染的天数的变化。
认真思考你会知道,lamda的现实意义就是该城市的卫生水平,衡量的是消毒,隔离这些措施执行得怎么样。
回到传染病模型,按照SI模型计算的结果,我们全人类都会患病,这好可怕!原因是我们忽略了一个很重要的因素,那就是我们有奋斗在一线的医护人员,我们会被治愈!所以SI模型只适合研究具有高传染风险又不能被治愈的病(比如HIV)。
但是对于其他病,我们是可以靠医疗和自身免疫系统康复的,那么紧接着的一个问题就是,被治愈后还会再被传染上嘛?根据这个问题的回答不同,我们有了两个不同的模型,SIR 和 SIS。现在可以揭晓,SIR的R的含义了,就是移出者(Removed),现实含义就是指被治愈后不会再被感染的人。 而SIS表示治愈后仍然还是易感者。下面我们用python来分别实现这两个模型。
SIS模型
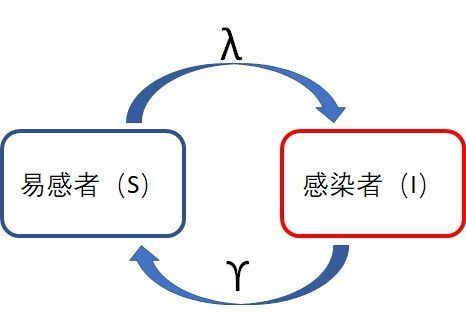
为了实现这个模型,我们需要引入新的一个参数,治愈率 γ \gamma γ。好啦,先上我们的新示意图:
和SI模型做比较,区别就是计算感染者的增加数时要减去被治愈的人数。
所以这时候每天的增加的感染者为: λ × i N × s − γ × i N \lambda \times i N \times s-\gamma \times i N λ×iN×s−γ×iN ,
增加的感染率为: λ × i × s − γ i \lambda \times i \times s-\gamma i λ×i×s−γi 。
模型完成啦,修改python代码:
# susceptiable ratio
s = np.zeros([T])
# infective ratio
i = np.zeros([T])
# contact rate
lamda = 1.0
# recover rate
gamma = 0.5
# initial infective people
i[0] = 45.0 / N
for t in range(T-1):
i[t + 1] = i[t] + i[t] * lamda * (1.0 - i[t]) - gamma*i[t]
运行代码,我们画出曲线(代码和SI模型的画图完全一样):
fig, ax = plt.subplots(figsize=(8,4))
ax.plot(i, c='r', lw=2)
ax.set_xlabel('Day',fontsize=20)
ax.set_ylabel('Infective Ratio', fontsize=20)
ax.grid(1)
plt.xticks(fontsize=20)
plt.yticks(fontsize=20);
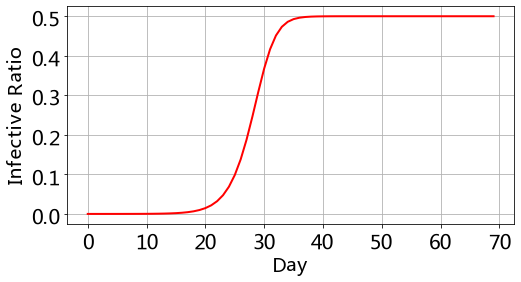
运行代码,我们画出曲线(代码和SI模型的画图完全一样)
可以看到,达到最大感染率的时间退后10天左右,最后感染和治愈达到动态平衡,人群中有始终有一半的人感染着。所以,SIS模型适合研究具有传染性和反复性的流行病,比如常见流感。同样的,感兴趣的话,改变lamda和gamma的值,观察曲线的变化。和lamda不同的是,gamma的现实意义就是对这种疾病的治疗水平。
SIR模型
加入了移出者,被治愈的病人不会再被传染,先上我们的新示意图:
SIR 模型
注意到这里,人群被分成了三类,不再只有I和S,所以相比于之前的模型,我们需要找到新的约束关系。现在我们需要分别计算三种人每天的增加量了:
- 易感者:每天都在被传染,所以一直在减少,减少量为被传染的人数: λ N i s \lambda N i s λNis
- 感染者:增加了被感染的人,减少了治愈的人: λ N i s − γ N i \lambda N i s-\gamma N i λNis−γNi
- 移出者:增加了治愈的人: γ N i \gamma N i γNi
建模完成,修改python代码,并且假设人群普遍易感,新型疾病,初始没有移出者。
# population
N = 1e7 + 10 + 5
# simuation Time / Day
T = 170
# susceptiable ratio
s = np.zeros([T])
# infective ratio
i = np.zeros([T])
# remove ratio
r = np.zeros([T])
# contact rate
lamda = 0.2586
# recover rate
gamma = 0.0821
# initial infective people
i[0] = 10.0 / N
s[0] = 1e7 / N
for t in range(T-1):
i[t + 1] = i[t] + i[t] * lamda * s[t] - gamma*i[t]
s[t + 1] = s[t] - lamda * s[t] * i[t]
r[t + 1] = r[t] + gamma*i[t]
fig, ax = plt.subplots(figsize=(10,6))
ax.plot(s, c='b', lw=2, label='S')
ax.plot(i, c='r', lw=2, label='I')
ax.plot(r, c='g', lw=2, label='R')
ax.set_xlabel('Day',fontsize=20)
ax.set_ylabel('Infective Ratio', fontsize=20)
ax.grid(1)
plt.xticks(fontsize=20)
plt.yticks(fontsize=20)
plt.legend();
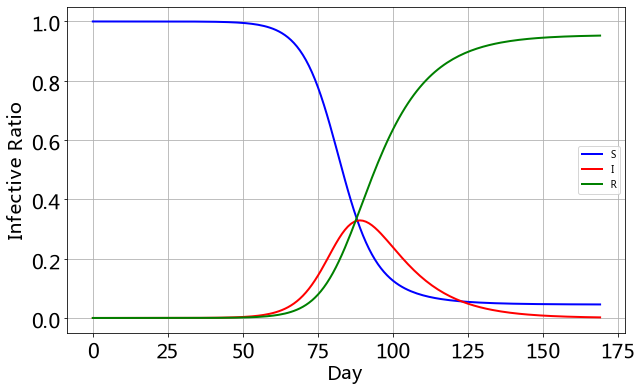
感染人数峰值发生在一个月左右,最大感染人数不到人群的20%, 但是最终人群的80%都会得此病(就是最终的移出者的比例)。SIR模型适合研究没有潜伏期的急性传染病,治疗后能够痊愈并具有抗病性。
到这里,虽然不准确,我们也可以先用SIR模型来分析一下此次疫情,武汉新型冠状病毒的传染病动力学!
模型有了,其实就是确定参数的问题。一开始就有人做了这个工作:
于教授给的参数是参考了非典的, γ = 0.0821 , λ = 0.2586 \gamma=0.0821,\lambda=0.2586 γ=0.0821,λ=0.2586,初始易感人数为一千万, 初始感染10人,初始移出者5人,那么我们的城市总人数 N = 1 e 7 + 10 + 5 N=1 e 7+10+5 N=1e7+10+5 , 带入我们的模型得到结果:
重现于教授的模型
高峰和尾声日期的推测基本相符。
# susceptiable ratio
s = np.zeros([T])
# infective ratio
i = np.zeros([T])
# removed ratio
r = np.zeros([T])
# birth ratio
b = 20.0 / N
# death ratio
d = 10.0 / N
# contact rate
y = 1.5
# recover rate
u = 0.8 # 1 / infective_period
# sigma = y / u
# initial infective people
i[0] = 45.0 / N
s[0] = 1 - i[0]
for t in range(T-1):
i[t+1] = i[t] + i[t] * y * s[t] - u*i[t] - d*i[t]
s[t+1] = s[t] - y * s[t] * i[t] + b - d*s[t]
r[t+1] = r[t] + u*i[t] - d*r[t]
plt.plot(i)
plt.plot(s)
plt.plot(r)
plt.plot(np.diff(i),ls='--')
[]
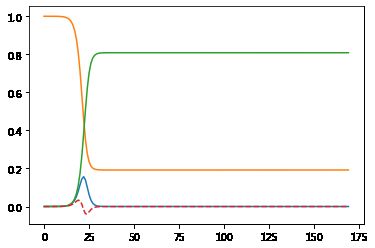
SEIR模型
但是,SIR模型和实际情况的出入会比较大,因为忽略了太多因素了,比如说潜伏期,比如说政策调控,药物,出生死亡等等。下面我们可以和前面一样,把潜伏期考虑进去,新增一个人群,叫潜伏者E(exposed):
SEIR模型
同样的我们需要计算各人群每天的增加量:
S:每天减少: λ N i s \lambda N i s λNis
E:每天增加传染,减少发病: λ N i s − σ N e \lambda N i s-\sigma N e λNis−σNe
I:每天增加发病,减少治愈: σ N e − γ N i \sigma N e-\gamma N i σNe−γNi
R:每天增加治愈: γ N i \gamma N i γNi
建模完成,修改我们的python程序,这里的 σ \sigma σ可以理解为潜伏期的倒数。给的4天。新型冠状病毒给目前临床的潜伏期是3-14天。
# population
N = 1e7 + 10 + 5
# simuation Time / Day
T = 170
# susceptiable ratio
s = np.zeros([T])
# exposed ratio
e = np.zeros([T])
# infective ratio
i = np.zeros([T])
# remove ratio
r = np.zeros([T])
# contact rate
lamda = 0.5
# recover rate
gamma = 0.0821
# exposed period
sigma = 1 / 4
# initial infective people
i[0] = 10.0 / N
s[0] = 1e7 / N
e[0] = 40.0 / N
for t in range(T-1):
s[t + 1] = s[t] - lamda * s[t] * i[t]
e[t + 1] = e[t] + lamda * s[t] * i[t] - sigma * e[t]
i[t + 1] = i[t] + sigma * e[t] - gamma * i[t]
r[t + 1] = r[t] + gamma * i[t]
fig, ax = plt.subplots(figsize=(10,6))
ax.plot(s, c='b', lw=2, label='S')
ax.plot(e, c='orange', lw=2, label='E')
ax.plot(i, c='r', lw=2, label='I')
ax.plot(r, c='g', lw=2, label='R')
ax.set_xlabel('Day',fontsize=20)
ax.set_ylabel('Infective Ratio', fontsize=20)
ax.grid(1)
plt.xticks(fontsize=20)
plt.yticks(fontsize=20)
plt.legend();

按照模型的结果,此次疫情可能真的要持续到 三四月份。这个接触率 λ \lambda λ 真的非常影响表现,模型给的是个常数,但是由于政府措施的原因,这应该是个变化的值。
还有治愈率 γ \gamma γ也是。没有完美的模型,但是随着考虑因素的增多,就会越来越接近实际情况,从而指导政府的疫情方针政策的制定。