图深度学习(GraphDL),下一个人工智能算法热点
https://www.toutiao.com/a6641731848772780548/
2019-01-02 11:11:41
原创: 专知
【导读】最近,DeepMind、Google大脑、MIT等各大研究机构相继发表了一系列的关于图深度学习的论文,包括关系性RNN、关系性深度强化学习、图卷积神经网络等, 这是否预示这是下一个AI算法热点。专知整理了最近图深度学习相关的热点论文,一文看晓。
1. Relational inductive biases, deep learning, and graph networks (图网络深度学习综述文章)
首先就是这篇由DeepMind、Google大脑、MIT、爱丁堡大学27个作者发表的37页关于关系归纳偏置、典型深度学习构件和图网络的综述文章,探讨了如何在深度学习架构中使用关系归纳偏置,有助于学习实体、关系及其组合规则,来有效解决传统“人工构造学习”和“端到端学习”的弊端,以增强学习的可解释性。
对此,一些知名的AI学者也对此做了点评。康纳尔大学数学博士/MIT博士后Seth Stafford说图神经网络(Graph NNs) 可能解决之前Judea Pearl提出的人工智能因果推断问题,贝叶斯网络之父Judea Pearl:要建立真正的人工智能,少不了因果推理。
论文地址:https://arxiv.org/abs/1806.01261
2. Relational Deep Reinforcement Learning(关系性深度强化学习)
近日,DeepMind 提出了一种「关系性深度强化学习」方法,并在星际争霸 2 中进行了测试,取得了最优水平。
论文链接:https://arxiv.org/abs/1806.01830
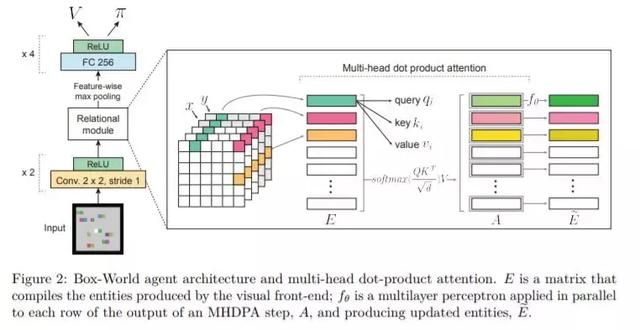
摘要:在本文中,我们介绍了一种深度强化学习方法,它可以通过结构化感知和关系推理提高常规方法的效率、泛化能力和可解释性。该方法使用自注意力来迭代地推理场景中实体之间的关系并指导 model-free 策略。实验结果表明,在一项名为「方块世界」的导航、规划新任务中,智能体找到了可解释的解决方案,并且在样本复杂性、泛化至比训练期间更复杂场景的能力方面提高了基线水平。在星际争霸 II 学习环境中,智能体在六个小游戏中达到了当前最优水平——在四个游戏中的表现超越了大师级人类玩家。通过考虑架构化归纳偏置,我们的研究为解决深度强化学习中的重要、棘手的问题开辟了新的方向。
更多解读,请看hardmaru的论文笔记:
https://yobibyte.github.io/files/paper_notes/rdrl.pdf
3. Relational recurrent neural networks(关系性循环神经网络)
DeepMind和伦敦大学学院的这篇论文提出关系推理模块RMC,能够在序列信息中执行关系推理,在WikiText-103, Project Gutenberg 和 GigaWord 数据集上达到了当前最佳性能。
摘要:基于记忆的神经网络通过利用长时间记忆信息的能力来建模时序数据。然而,目前还不清楚它们是否有能力利用它们记得的信息进行复杂的关系推理。在这篇论文中,DeepMind和伦敦大学学院的研究人员首先证实一种直觉想法,即标准的记忆架构在一些涉及关系推理的任务上很困难。然后,研究者通过使用一个新的记忆模块——Relational Memory Core(RMC)——来改进这种缺陷,该模块采用multi-head dot product attention来允许记忆交互。最后,研究者在一系列任务上测试RMC,这些任务可以从跨序列信息的更强大的关系推理中获益,并且在RL领域(例如Mini PacMan)、程序评估和语言建模中显示出巨大的受益,在WikiText-103、Project Gutenberg和GigaWord数据集上获得state-of-the-art的结果。
论文地址:https://arxiv.org/abs/1806.01822
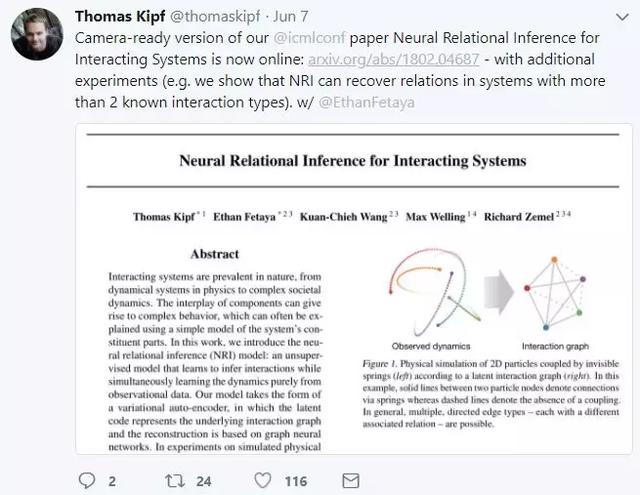
4. Neural Relational Inference for Interacting Systems
这篇由阿姆斯特丹大学的Thomas Kipf提出发表的ICML2018论文,神经关系推理(NRI)模型——交互系统神经网络关系推理,潜在交互图推断。
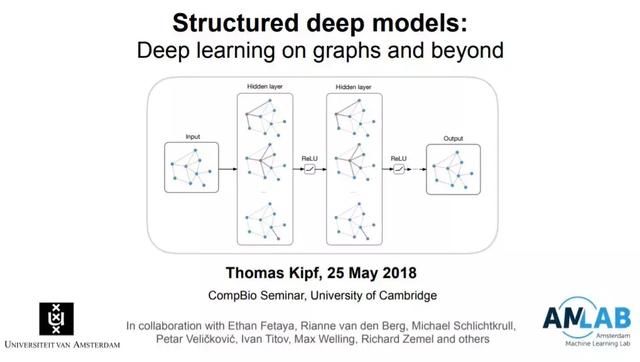
Thomas Kipf准备加入 Google DeepMind实习,在图深度学习方面有着深厚研究,之前他有一份结构化深度学习的教程,非常值得一看,教程地址:
http://tkipf.github.io/misc/SlidesCambridge.pdf
Graph Convolutional Neural Networks教程:https://tkipf.github.io/graph-convolutional-networks/
5. Videos as Space-Time Region Graphs
这篇由卡耐基梅隆大学(CMU)的王小龙发表的,把video表达成为一个roi proposal组成的graph,在上面定义local和nonlocal edges,做graph convolution。
论文地址:https://arxiv.org/abs/1806.01810