第四讲 Matlab/Simulink入门——连续系统仿真实例

1、连续系统基本概念

1.1 连续系统

  连续系统： 是指系统输出时间上连续变化，而不是仅在离散时刻采样取值。对于满足以下条件的系统，我们称之为连续系统：
  （1）系统输出连续变化，变化的时间间隔为无穷小量。
  （2）存在系统输入或输出的微分项。
  （3） 系统具有连续状态。
  设连续系统的输入变化量为$u(t)$，其中$t$为连续取值的时间变量，系统的输出为$y(t)$，连续系统的一般数学描述为：
$$y(t)=f(u(t),t)$$
  微分方程形式为：
$$\frac{\partial x}{\partial t}=f(x(t),u(t),t)$$
$$y(t)=g(x(t),u(t),t)$$

1.2 线性连续系统

   线性连续系统： 对满足以下两个条件的连续系统，我们称为线性连续系统。
  (1)、齐次性： 对于连续系统$y(t)=T\{u(t)\},t=0,1,2...$，如果对任意的输入$u(t)$与给定的常数$\alpha$，下面的式子总成立：
$$T\{\alpha u(t)\}=\alpha T\{u(t)\}$$
则称系统满足齐次性。
  (2)、叠加性： 对于系统对于输出$u_1(t)$和$u_2(t)$，输出分别为$y_1(t)$ 和$y_2(t)$，总有下面的式子成立：
$$T\{u_1(t)+u_2(t)\}=T\{u_1(t)\}+T\{u_2(t)\}$$
则称系统满足叠加性。

1.3 Laplace变换

  $Laplace变换$： 对于连续信号$u(t)$，其$Laplace$变换定义为$U(s)={\int }_{-\infty }^{\infty }u(t)e^{-st}\mathrm{d}t$。一般而言，系统的输入时间$t\ge 0$，这时$U(s)={\int }_0^{\infty }u(t)e^{-st}\mathrm{d}t$。一般简记为$U(s)=L(u(t))$。
  $Laplace变换$具有如下两个重要性质：
  (1)、线性关系： $Laplace$变换同时满足齐次性和叠加性，即：
$$U\{\alpha u_1(t)+\beta u_2(t)\}=\alpha U\{u_1(t)\}+\beta U\{u_2(t)\}$$
  (2)、设连续信号$u(t)$的$Laplace$变换为$U(s)$，则$\frac{\partial u}{\partial t}$的$Laplace$变换为$sU(t)$。
  线性连续系统的另一个模型为状态空间模型：
$$\{\begin{array}{l}\frac{\partial u}{\partial t}=Ax(t)+Bu(t)\\ y(t)=Cx(t)+Du(t)\end{array}$$

2、蹦极模型（例1）仿真

2.1 蹦极模型

 【例1】蹦极跳是一种挑战身体极限的运动，蹦极者系着一根弹力绳从高处的桥梁（或山崖等）向下跳。在下落的过程中，蹦极者几乎处于失重状态。按照牛顿运动定律，自由下落的物体的位置由下面的式子确定：
$$m\frac{{\partial }^{2}x}{\partial t^2}=mg-a_1\frac{\partial x}{\partial t}-a_2\left|\frac{\partial x}{\partial t}\right|\frac{\partial x}{\partial t}$$
  其中m为物体质量，g为重力加速度，x为物体的位置，$a_1$ 、$a_2$表示空气阻力的系数。
  现选择蹦极者起跳位置为起点（即x=0处），低于起点位置为正，高于起点为负。如果物体系在一个弹性系数为$k$的弹力绳索上，绳索的原始长度为$x_0$，则其对下落物体位置的作用力为:
$$b(x)=\{\begin{array}{l}-k(x-x_0),x>x_0\\ 0,x\le x_0\end{array}$$
  设蹦极者起跳位置距离地面 $80m$，绳索原始长度$x0=30m$，蹦极者起始速度为 0，即。其余参数分别为$k=18.45,a_1=1.3,a_2=1.1,m=70kg,=9.8m/s^2$。试建立蹦极跳系统的Simulink仿真模型，并对系统进行仿真，分析此蹦极跳系统是否安全。

2.2 建模

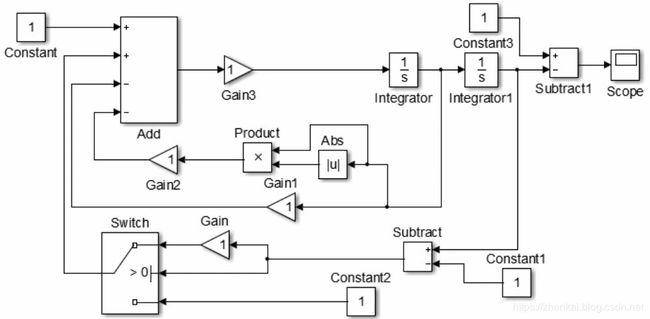
  建立蹦极跳系统的Simulink仿真模型。根据系统的数学描述选择合适的Simulink系统模块，建立此蹦极跳系统的Simulink模型，如上图所示。
  Constant模块：用于表示蹦极者重力$mg$。
  Constant1模块：用于表示绳索原始长度$x_0$。
  Constant2模块：用于表示当$x\le x_0$时函数$b(x)$的取值，即$0$。
  Constant3模块：用于表示蹦极者起始位置相对地面的距离。
  Gain模块：用于表示弹性系数的负数，即$-k$。
  Gain1模块：用于表示参数$a_1$。
  Gain2模块：用于表示参数$a_2$。
  Gain3模块：用于表示蹦极者质量的倒数，即$\frac{1}{m}$。
  Abs 模块：来自Math Operations子库，用于对信号取绝对值。
  Integrator模块和Integrator1模块：来自Continuous子库，用于对信号进行积分。Integrator模块的输入信号为，输出为；Integrator1模块的输入信号为，输出为$x$。
  Switch 模块：来自Signal Routing 子库，用于构建分段函数$b(x)$。

2.3 模型参数设置

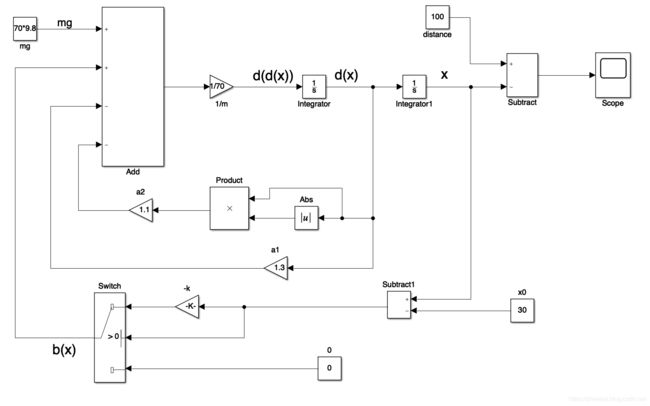
  mg模块：常值设为70*9.8。
  0模块：常值设为0。
  x0模块：常值设为30。
  distance模块：常值设为80。
  -k模块：增益设为-18.45。
  a1模块：增益设为1.3。
  a2模块：增益设为1.1。
  1/m模块：增益设为1/70。
  Switch模块：Threshold设为默认值，判断准则设为u2>Threshold，如图4-19所示。
  Integrator模块和Integrator1模块：由于设初始位置和初始速度均为0，故这两个模块的初始值设为默认值（零）即可。

2.4 系统仿真

  仿真时间设置为50s，然后运行，结果如图所示。

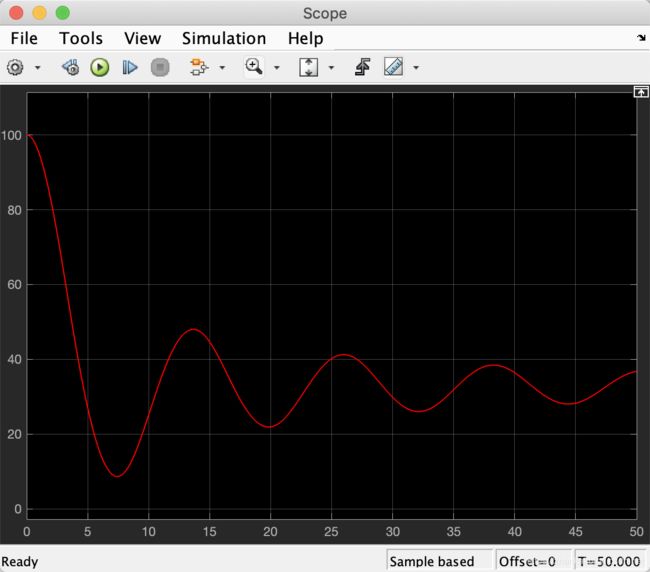
  从图中可以看到，蹦极者相对地面的距离存在小于零的情况，也就是说此蹦极跳系统对于70kg的蹦极者来说不安全的，蹦极者会触碰到地面。

3、比例微分控制器（例2）仿真

3.1 比例微分控制器模型

 【例2】比例微分控制器系统，其数学描述为：
$$u(t)=K_{p}e(t)+K_d\frac{\partial e}{\partial t}$$
  现有一个执行机构，其传递函数为：
$$\frac{1}{(s-1.1)(s+1.1)}$$
  显然，它是发散的，不稳定的，其开环阶跃响应曲线如图所示。

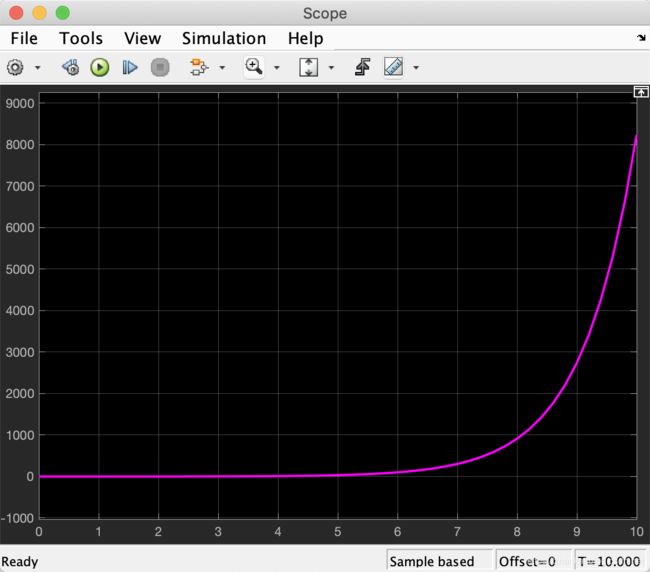
3.2 建模

  Derivative模块：来自Continuous子库，微分器，其输入为$e(t)$，输出为。
  Gain模块：控制器比例项系数，即$K_p=15$。
  Gain1模块：控制器微分项系数，即$K_d=2$。
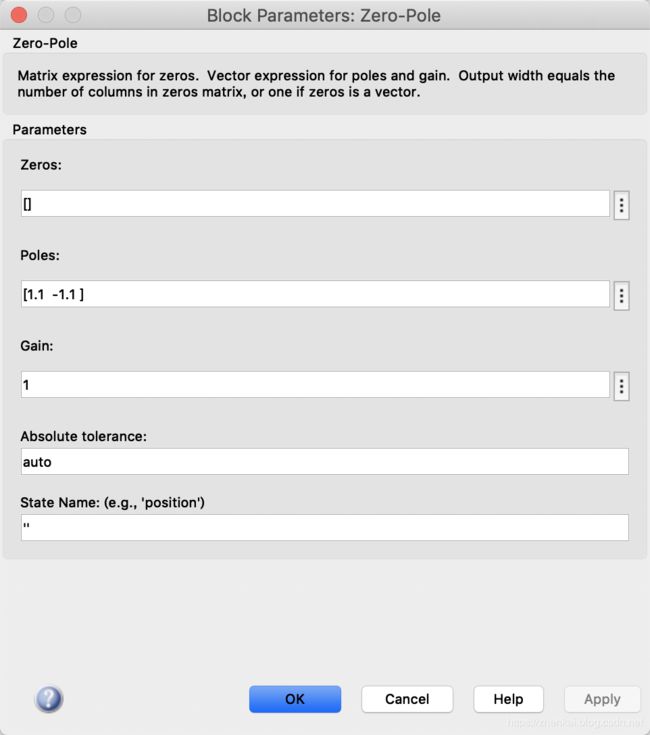
  Zero-Pole 模块：设置Zeros 零点为[]，Poles 极点为[1.1 -1.1]，Gain 增益为1，其余默认，如图所示。

3.3 模型仿真

  仿真时间设置为20s。
  最大仿真步长设置为0.01。
  绝对误差设置为1e-6。

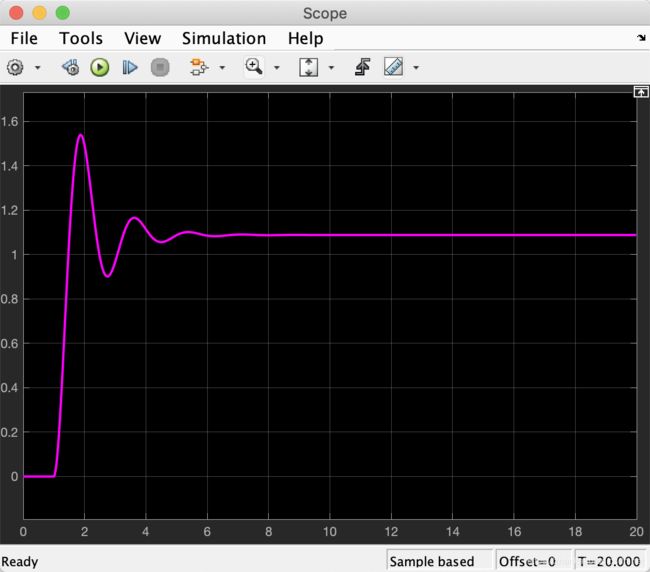
  仿真结果如图所示，在阶跃信号的作用下，系统不断地对位置误差进行控制修正，最终系统达到了稳定状态，可以通过调整$K_p$、$K_d$以获得更好的性能。