LeetCode+剑指 二叉树总结
<font color=#FF0000 >红色
<font color=#008000 >绿色
<font color=#0000FF >蓝色
ღღღ
二叉树的遍历总结
(前序、中序、后序、层序、 之字形层序、垂直遍历)
三种递归遍历
void preorder(TreeNode* root, vector<int>& path){
if(root==NULL) return;
path.push_back(root->val); //打印根节点
preorder(root->left,path);
perorder(root->right,path);
}
void inorder(TreeNode* root, vector<int>& path){
if(root==NULL) return;
inorder(root->left,path);
path.push_back(root->val);
inorder(root->right,path);
}
void postorder(TreeNode* root, vector<int>& path){
if(root==NULL) return;
postorder(root->left,path);
postorder(root->right,path);
path.push_back(root->val);
}
三种非递归遍历
前序遍历(根-左-右)
根据前序遍历访问的顺序,优先访问根结点,然后再分别访问左结点和右结点。即对于任一结点,其可看作是根结点,因此可以直接访问,访问完之后,若其左结点不为空,按相同规则访问它的左子树;当访问其左子树时,再访问它的右子树。因此其处理过程如下:
对于任一结点P:
1)访问结点P,并将结点P入栈;
2)判断结点P的左孩子是否为空,若为空,则取栈顶结点并进行出栈操作,并将栈顶结点的右孩子置为当前的结点P,循环至1);若不为空,则将P的左孩子置为当前的结点P;
3)直到P为NULL并且栈为空,则遍历结束。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
//非递归前序遍历
class Solution{
public:
vector<int> preorderTraversal(TreeNode* root){
vector<int> path;
if(root == nullptr) return path;
stack<TreeNode*> s;
TreeNode *p = root;
while(p || !s.empty()){
if(p){ //当左结点不为空时
path.push_back(p->val); //访问当前结点(父结点)
s.push(p); //入栈
p = p->left; //指向下一个左结点
}
else{
p = s.top();
s.pop(); //出栈
p = p->right; //指向右结点
}
}
return path;
}
}
中序遍历:(左 - 根 - 右)
根据中序遍历的顺序,对于任一结点,优先访问其左孩子,而左孩子结点又可以看做一根结点,然后继续访问其左孩子结点,直到遇到左孩子结点为空的结点才进行访问,然后按相同的规则访问其右子树。因此其处理过程如下:
对于任一结点P,
1)若其左孩子不为空,则将P入栈并将P的左孩子置为当前的P,然后对当前结点P再进行相同的处理;
2)若其左孩子为空,则取栈顶元素并进行出栈操作,访问该栈顶结点,然后将当前的P置为栈顶结点的右孩子;
3)直到P为NULL并且栈为空则遍历结束
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
//非递归中序遍历
class Solution{
public:
vector<int> inorderTraversal(TreeNode* root){
vector<int> path;
if(root == nullptr) return path;
stack<TreeNode*> s;
TreeNode *p = root;
while(p || !s.empty()){
if(p){ //当左结点不为空时
s.push(p); //入栈
p = p->left; //指向下一个左结点
}
else{ //当左结点为空时
p = s.top();
path.push_back(p->val); //访问栈顶元素(父结点)
s.pop(); //出栈
p = p->right; //指向右结点
}
}
return path;
}
}
后序遍历:(左 - 右 - 根)
要保证根结点在左孩子和右孩子访问之后才能访问,因此对于任一结点P,先将其入栈。
(1)如果P不存在左孩子和右孩子,则可以直接访问它;
(2)或者P存在左孩子或者右孩子,但是其左孩子和右孩子都已被访问过了,则同样可以直接访问该结点。
(3)若非上述两种情况,则将P的右孩子和左孩子依次入栈,这样就保证了每次取栈顶元素的时候,左孩子在右孩子前面被访问,左孩子和右孩子都在根结点前面被访问。
//非递归后序遍历
vector<int> postorderTraversal(TreeNode* root){
vector<int> result;
stack<TreeNode*> s;
if(root== nullptr) return result;
TreeNode* p; //当前结点指针
TreeNode* pre = nullptr; //用于记录上一次访问的结点
s.push(root); //根结点指针入栈
while(!s.empty()){ //不为空时才会入栈,故p不可能为nullptr,无需像之前加p的判断
p = s.top(); // 指向栈顶元素
bool temp1 = p->left == nullptr && p->right == nullptr; //如果当前结点为叶子结点
bool temp2 = pre != nullptr && (pre == p->left || pre == p->right); //或者当前结点的左结点和右结点都已被访问过了(若pre=p->left说明右结点为空,因为栈中按照根右左这样的顺序入栈,根左这种结构才能出现这种情况)
if(!temp1 && !temp2)//如果不是上面两种情况,直接入栈
{
//先将右结点入栈,再将左结点入栈,这样可以保证之后访问时先访问左结点在访问右结点
if(p->right) s.push(p->right); //右结点入栈
if(p->left) s.push(p->left); //左结点入栈
}
else
{
result.push_back(p->val); //访问顺序:左、右、根
s.pop();
pre = p; //保存刚刚访问过的结点
}
}
return result;
}
参考:
《更简单的非递归遍历二叉树的方法》
ღღღ
层次遍历
(1)剑指32 - I. 从上到下打印二叉树【中等】
从上到下打印出二叉树的每个节点,同一层的节点按照从左到右的顺序打印。
例如:
给定二叉树: [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回:
[3,9,20,15,7]
思路:层次遍历。用一个队列。
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};*/
class Solution {
public:
vector<int> PrintFromTopToBottom(TreeNode* root) {
vector<int> res;//保存要打印的数。
if(root==NULL)
return res;
queue<TreeNode*> q; //新建一个队列。
q.push(root);
while(!q.empty()){
res.push_back(q.front()->val);
if(q.front()->left!=NULL)
q.push(q.front()->left);
if(q.front()->right!=NULL)
q.push(q.front()->right);
q.pop(); //弹出第一个元素。
}
return res;
}
};
ღღღ
(2)剑指32 - II. 从上到下(分行)打印二叉树 II
从上到下按层打印二叉树,同一层的节点按从左到右的顺序打印,每一层打印到一行。
例如:
给定二叉树: [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回其层次遍历结果:
[
[3],
[9,20],
[15,7]
]
思路:层次遍历。用一个队列。用一个临时vector存放每一层的值。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> res;//保存要打印的数。注意vector里面有vector
if(root==NULL)//这个条件其实很重要,有时候不写就出错
return res;
queue<TreeNode*> q; //新建一个队列。
q.push(root); //先把根节点放进去
while(!q.empty()){
vector<int> tmp; //定义一个临时vector
int len=q.size();//只能在这求,如果写到for循环里 for(int i = 0; i < q.size(); ++i),它大小会变化,结果出错。
for(int i = 0; i < len; ++i){
tmp.push_back(q.front()->val);
if(q.front()->left!=NULL)
q.push(q.front()->left);
if(q.front()->right!=NULL)
q.push(q.front()->right);
q.pop(); //弹出第一个元素。
}
res.push_back(tmp);
}
return res;
}
};
ღღღ
(3)剑指32 - III. 从上到下(之字形)打印二叉树 III(中等)
请实现一个函数按照之字形顺序打印二叉树,即第一行按照从左到右的顺序打印,第二层按照从右到左的顺序打印,第三行再按照从左到右的顺序打印,其他行以此类推。
例如:
给定二叉树: [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回其层次遍历结果:
[
[3],
[20,9],
[15,7]
]
方法一:用一个队列,虽然方便 ,但用reverse的时候复杂度要增加
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> res;//保存要打印的数。注意vector里面有vector
if(root==NULL)
return res;
queue<TreeNode*> q; //新建一个队列。
q.push(root); //先把根节点放进去
bool flag=false; //判断是否为偶数行,flag=false代表奇数行,flag=true代表偶数行
while(!q.empty()){
vector<int> tmp; //定义一个临时vector。行容器,用于存入当前行输出的结果
int len=q.size();
for(int i = 0; i < len; ++i){
tmp.push_back(q.front()->val);
if(q.front()->left!=NULL)
q.push(q.front()->left);
if(q.front()->right!=NULL)
q.push(q.front()->right);
q.pop(); //弹出第一个元素。
}
if(flag) reverse(tmp.begin(),tmp.end()); //是偶数行就反转顺序
flag=!flag; //改变flag的值
res.push_back(tmp);
}
return res;
}
};
方法二:用两个栈,时间换空间
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* pRoot) {
vector<vector<int> > vec; //存放结果
if(pRoot == NULL) return vec; //这个东西必须写,否则超时!!!
stack<TreeNode*> stk1, stk2; //定义两个栈
stk1.push(pRoot);
vector<int> tmp;
while(!stk1.empty() || !stk2.empty()){
while(!stk1.empty()){ //如果栈1不为空 //while
TreeNode* pNode = stk1.top();
tmp.push_back(pNode->val); //tmp.push(skt1.top()->left
if(pNode->left) stk2.push(pNode->left);
if(pNode->right) stk2.push(pNode->right);
stk1.pop();
}
if(tmp.size()){ //if
vec.push_back(tmp);
tmp.clear();
}
while(!stk2.empty()){ //如果栈2不为空
TreeNode* pNode = stk2.top();
tmp.push_back(pNode->val);
if(pNode->right) stk1.push(pNode->right); //注意,放入的顺序要反
if(pNode->left) stk1.push(pNode->left);
stk2.pop();
}
if(tmp.size()){
vec.push_back(tmp);
tmp.clear();
}
}
return vec;
}
};
ღღღ
(4)314.二叉树的竖直遍历【中等】☒ (上锁)
还不会,不懂pair是啥类型。
Examples 1:
Input: [3,9,20,null,null,15,7]
3
/\
/ \
9 20
/\
/ \
15 7
Output:
[
[9],
[3,15],
[20],
[7]
]
Examples 2:
Input: [3,9,8,4,0,1,7]
3
/\
/ \
9 8
/\ /\
/ \/ \
4 01 7
Output:
[
[4],
[9],
[3,0,1],
[8],
[7]
]
Examples 3:
Input: [3,9,8,4,0,1,7,null,null,null,2,5] (0's right child is 2 and 1's left child is 5)
3
/\
/ \
9 8
/\ /\
/ \/ \
4 01 7
/\
/ \
5 2
Output:
[
[4],
[9,5],
[3,0,1],
[8,2],
[7]
]
/* 掌握
问题:二叉树的垂直遍历
方法:层序遍历,并给每个结点赋上列号(对于每列元素而言,层序遍历访问的先后顺序满足垂直遍历规律)
把根节点给个序号0,然后开始层序遍历,
凡是左子节点则序号减1,右子节点序号加1,
这样我们可以通过序号来把相同列的节点值放到一起
*/
class Solution
{
public:
vector<vector<int>> verticalOrder(TreeNode* root)
{
vector<vector<int>> res;
if (!root) return res;
map<int, vector<int>> m; //构建存储<序号,遍历序列>对的map
queue<pair<int, TreeNode*>> q; //构建存储<序号,结点>对的队列
q.push({0, root}); //根结点入队,根结点序号设为0
while (!q.empty()) //层序遍历
{
auto a = q.front();
m[a.first].push_back(a.second->val); //访问当前结点,将结点值push到相同列的容器中
q.pop(); //出队
//将下一层结点入队
if (a.second->left) q.push( {a.first - 1, a.second->left} ); //左结点序号减一
if (a.second->right) q.push( {a.first + 1, a.second->right} ); //右结点序号加一
//下一层的结点排在上一层结点之后
}
for (auto mi : m) //将map中遍历序列按顺序push到结果容器中(map内部会自动排序,序号从小到大排列遍历序列)
{
res.push_back(mi.second);
}
return res;
}
};
ღღღ
(5)剑指55 - I. 二叉树的深度(LC104)
输入一棵二叉树的根节点,求该树的深度。从根节点到叶节点依次经过的节点(含根、叶节点)形成树的一条路径,最长路径的长度为树的深度。
例如:
给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回它的最大深度 3 。
递归
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
int maxDepth(TreeNode* pRoot) {
if(pRoot==NULL){//递归的出口
return 0;
}
int nleft=maxDepth(pRoot->left);//用递归的方法,左子树的深度
int nright=maxDepth(pRoot->right); //右子树的深度
return (nleft>nright)? (nleft+1):(nright+1); //更大的那个值+1
//return 1 + max(depth_left, depth_right);
}
};
(6)剑指55 - II. 平衡二叉树(LC110)
输入一棵二叉树的根节点,判断该树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的深度相差不超过1,那么它就是一棵平衡二叉树。
示例 1:
给定二叉树 [3,9,20,null,null,15,7]
3
/ \
9 20
/ \
15 7
返回 true 。
示例 2:
给定二叉树 [1,2,2,3,3,null,null,4,4]
1
/ \
2 2
/ \
3 3
/ \
4 4
返回 false 。
法1:递归,先序遍历
(好理解)先序遍历每一个节点,并比较左右子树高度,如果有>1则返回false (在上一题 “二叉树的深度” 的基础上进行判断)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
bool isBalanced(TreeNode* root) {
if (root == NULL) return true;//如果该子树为空,则一定是平衡的(因为没有左右子树)
if (abs(getHeight(root->left) - getHeight(root->right)) > 1) return false;
return isBalanced(root->left)&& isBalanced(root->right); //都返回true,则返回true
}
//获取深度 套路
int getHeight(TreeNode* pRoot) {
if(pRoot==NULL){//递归的出口
return 0;
}
int nleft=getHeight(pRoot->left);//用递归的方法,左子树的深度
int nright=getHeight(pRoot->right); //右子树的深度
return (nleft>nright)? (nleft+1):(nright+1); //更大的那个值+1
//return 1 + max(depth_left, depth_right);
}
};
法2 (递归)(不好理解)/后序遍历/使用后序遍历的方式遍历二叉树的每个节点,那么在遍历到一个节点之前我们就已经遍历了它的左右子树。只要在每个节点的时候记录它的深度(某一节点的深度等于它到叶节点的路径的长度)就可以判断每个节点是不是平衡的
class Solution {
public:
bool IsBalanced_Solution(TreeNode* pRoot) {
if (pRoot== nullptr) return true;
int depth=0;
return IsBalanced(pRoot,depth);
}
bool IsBalanced(TreeNode* pRoot,int &depth){
if(pRoot==NULL)
return true;
int left=0;
int right=0;
if(IsBalanced(pRoot->left,left) && IsBalanced(pRoot->right,right)){
int diff=left-right;
if(diff<=1 && diff>=-1){ //abs(diff) <= 1
depth=(left>right? left:right)+1;
return true;
}
}
return false;
}
};
ღღღ
(7)剑指28. 对称的二叉树(LC101)
请实现一个函数,用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样,那么它是对称的。
例如,二叉树 [1,2,2,3,4,4,3] 是对称的。
1
/ \
2 2
/ \ / \
3 4 4 3
但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:
1
/ \
2 2
\ \
3 3
示例 1:
输入:root = [1,2,2,3,4,4,3]
输出:true
示例 2:
输入:root = [1,2,2,null,3,null,3]
输出:false
递归
递归结束条件:
都为空指针则返回 true
只有一个为空则返回 false
两个指针当前节点值不相等 返回false
递归过程:
判断 A 的右子树与 B 的左子树是否对称
判断 A 的左子树与 B 的右子树是否对称
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
bool isSymmetric(TreeNode* root) {
return isMirror(root,root); //把两个根节点传入,相当于有两个相同的二叉树
}
bool isMirror(TreeNode* proot1, TreeNode* proot2){
if(proot1==NULL && proot2==NULL) return true;//递归的三个出口
if(proot1==NULL || proot2==NULL) return false;// 如果其中之一为空,也不是对称的
// 走到这里二者一定不为空
if(proot1->val != proot2->val) return false;
//左结点的左子树和右结点的右子树相等,左结点的右子树和右结点的左子树相等时返回turn
return isMirror(proot1->left,proot2->right) && isMirror(proot1->right,proot2->left);
}
};
(8)剑指27. 二叉树的镜像(LC226)
请完成一个函数,输入一个二叉树,该函数输出它的镜像。
例如输入:
4
/ \
2 7
/ \ / \
1 3 6 9
镜像输出:
4
/ \
7 2
/ \ / \
9 6 3 1
示例 1:
输入:root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]
递归
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* mirrorTree(TreeNode* pRoot) {
if (pRoot == NULL) return NULL;
//if (pRoot->left==NULL&&pRoot->right==NULL) return;
swap(pRoot->left, pRoot->right);
mirrorTree(pRoot->left);
mirrorTree(pRoot->right);
return pRoot;
}
};
栈
模型:栈模拟二叉树的先序遍历
循环结束条件:栈为空
实现操作:交换当前结点的左右子树
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* mirrorTree(TreeNode* pRoot) {
if (pRoot == NULL)return NULL;
stack<TreeNode*> st;
//TreeNode* p = NULL;
st.push(pRoot);
while (st.size())
{
TreeNode* p = st.top();
st.pop();
swap(p->left, p->right);
if (p->left)st.push(p->left);
if (p->right)st.push(p->right);
}
return pRoot;
}
};
同理,队列
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* mirrorTree(TreeNode* pRoot) {
if (pRoot == NULL)return NULL;
queue<TreeNode*> st;
//TreeNode* p = NULL;
st.push(pRoot);
while (st.size())
{
TreeNode* p = st.front();
st.pop();
swap(p->left, p->right);
if (p->left)st.push(p->left);
if (p->right)st.push(p->right);
}
return pRoot;
}
};
ღღღ
(9)剑指26. 树的子结构【中等】(LC572 no)
输入两棵二叉树A和B,判断B是不是A的子结构。(约定空树不是任意一个树的子结构)
B是A的子结构, 即 A中有出现和B相同的结构和节点值。
例如:
给定的树 A:
3
/ \
4 5
/ \
1 2
给定的树 B:
4
/
1
返回 true,因为 B 与 A 的一个子树拥有相同的结构和节点值。
示例 1:
输入:A = [1,2,3], B = [3,1]
输出:false
示例 2:
输入:A = [3,4,5,1,2], B = [4,1]
输出:true
递归
思路:
首先要遍历A找出与B根节点一样值的节点R
然后判断树A中以R为根节点的子树是否包含和B一样的结构
class Solution {
public:
bool isSubStructure(TreeNode* A, TreeNode* B) {
bool res = false;
//当TreeA和TreeB都不为零的时候,才进行比较。否则直接返回false
if (A!=NULL && B!=NULL)
{
//如果找到了对应TreeB的根节点的点
if (A->val == B->val)
//以这个根节点为为起点判断是否包含TreeB
res = helper(A, B);
//如果找不到,那么就再去TreeA的左子树当作起点,去判断是否包含TreeB
if (!res)
res = isSubStructure(A->left, B);
//如果还找不到,那么就再去TreeA的右子树当作起点,去判断是否包含TreeB
if (!res)
res = isSubStructure(A->right, B);
}
// 返回结果
return res;
}
bool helper(TreeNode* A, TreeNode* B)
{
//如果TreeB已经遍历完了都能对应的上,返回true
if (B==NULL)
return true;
//如果TreeB还没有遍历完,TreeA却遍历完了。返回false
if (A==NULL)
return false;
//如果其中有一个点没有对应上,返回false
if (A->val != B->val)
return false;
//如果根节点对应的上,那么就分别去子节点里面匹配
return helper(A->left, B->left) && helper(A->right, B->right);
}
};
ღღღ
(10)剑指34. 二叉树中和为某一值的路径【中等】(LC113)
输入一棵二叉树和一个整数,打印出二叉树中节点值的和为输入整数的所有路径。从树的根节点开始往下一直到叶节点所经过的节点形成一条路径。要求输出所有路径
示例:
给定如下二叉树,以及目标和 sum = 22,
5
/ \
4 8
/ / \
11 13 4
/ \ / \
7 2 5 1
返回:
[
[5,4,11,2],
[5,8,4,5]
]
思路:递归。先序遍历/深度优先搜索/回溯
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};*/
class Solution {
public:
vector<vector<int> > FindPath(TreeNode* root,int expectNumber) {
find(root, expectNumber);
return res;
}
vector<vector<int>> res;
vector<int> path;
void find(TreeNode* root, int sum)
{
if (root == NULL)return; //啥都不干,返回上一步
path.push_back(root->val);
if (!root->left && !root->right && sum == root->val)//!root->left && !root->right 两个条件是保证更新到了最下面的叶结点。
res.push_back(path); //所有的一下全放进去
else
{
if (root->left)
find(root->left, sum - root->val);
if (root->right)
find(root->right, sum - root->val);
}
path.pop_back(); // 回溯su 当成栈使用了
}
};
ღღღ
(11)LC112. 路径总和
给定一个二叉树和一个目标和,判断该树中是否存在根节点到叶子节点的路径,这条路径上所有节点值相加等于目标和。
说明: 叶子节点是指没有子节点的节点。不需要输出路径
示例:
给定如下二叉树,以及目标和 sum = 22,
5
/ \
4 8
/ / \
11 13 4
/ \ \
7 2 1
返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。
注意:在bool函数中,必须有return什么什么,,return true, return false
思路:深度优先搜索# 只要求返回true或false,只判断是否存在,因此不需要记录路径
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
bool DFS(TreeNode* root, int sum){
if(root == NULL){
return false;
}
if(!root->left &&!root->right){
if(root->val == sum){
return true;
}
}
return (DFS(root->left, sum-root->val) || DFS(root->right, sum -root->val)); //只要有一个路径通就行
}
bool hasPathSum(TreeNode* root, int sum) {
return DFS(root, sum);
}
};
或写成
class Solution {
public:
bool hasPathSum(TreeNode* root, int sum) {
if(root == NULL){
return false; //都走到子节点为空了,肯定为false了
}
if(!root->left &&!root->right){
if(root->val == sum){
return true;
}
}
return (hasPathSum(root->left, sum-root->val) || hasPathSum(root->right, sum -root->val));
}
};
ღღღ
(12)124. 二叉树中的最大路径和【困难】
给定一个非空二叉树,返回其最大路径和。
本题中,路径被定义为一条从树中任意节点出发,达到任意节点的序列。该路径至少包含一个节点,且不一定经过根节点。
示例 1:
输入: [1,2,3]
1
/ \
2 3
输出: 6
示例 2:
输入: [-10,9,20,null,null,15,7]
-10
/ \
9 20
/ \
15 7
输出: 42
思路:
果然是hard,看了半天!
最大路径和:根据当前节点的角色,路径和可分为两种情况:
一:以当前节点为根节点
1.只有当前节点
2.当前节点+左子树
3.当前节点+右子书
4.当前节点+左右子树
这四种情况的最大值即为以当前节点为根的最大路径和
此最大值要和已经保存的最大值比较,得到整个树的最大路径值
二:当前节点作为父节点的一个子节点
和父节点连接的话则需取【单端的最大值】
1.只有当前节点
2.当前节点+左子树
3.当前节点+右子书
这三种情况的最大值
"""
代码:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
int res=INT_MIN;
int maxPathSum(TreeNode* root) {
maxValue(root);
return res;
}
int maxValue( TreeNode* root){
if(root==NULL) return 0; //递归出口
int leftValue=maxValue(root->left); //递归结果当然是整数了
int rightValue=maxValue(root->right);
int value1=root->val;
int value2=root->val + leftValue;
int value3=root->val + rightValue;
int value4=root->val + leftValue + rightValue;
int maxValue=max(max(max(value1,value2),value3),value4);//4个值的最大值
res = max(maxValue, res); //更新全局最大值
return max(max(value1,value2),value3);//因为要返回到父节点,所以返回单端的最大值.只能取left和right中较大的那个值,而不是两个都要
}
};
(13)剑指8 二叉树(中序遍历)的下一个结点(LC无)
题目描述
给定一个二叉树和其中的一个结点,请找出中序遍历顺序的下一个结点并且返回。注意,树中的结点不仅包含左右子结点,同时包含指向父结点的指针。
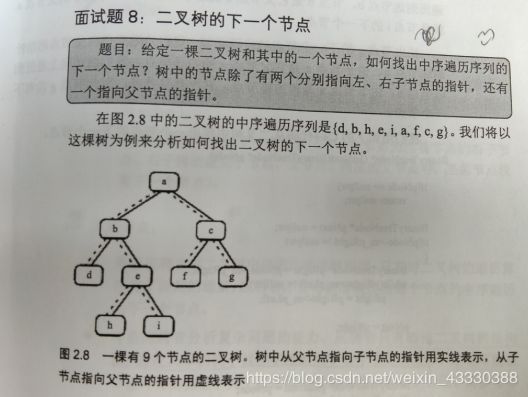
分析二叉树的下一个节点,一共有以下情况:
1.二叉树为空,则返回空;
2.节点右孩子存在,则设置一个指针从该节点的右孩子出发,一直沿着指向左子结点的指针找到的叶子节点即为下一个节点;比如b的下个节点是h,a的下个节点是f。
3.节点不是根节点。如果该节点是其父节点的左孩子,则返回父节点;否则继续向上遍历其父节点的父节点,重复之前的判断,返回结果。代码如下:
/*
struct TreeLinkNode {
int val;
struct TreeLinkNode *left;
struct TreeLinkNode *right;
struct TreeLinkNode *next;
TreeLinkNode(int x) :val(x), left(NULL), right(NULL), next(NULL)
}
};
*/
class Solution {
public:
TreeLinkNode* GetNext(TreeLinkNode* pNode)
{
if(pNode==NULL)
return NULL;
if(pNode->right!=NULL)//右节点存在。有右子树时,下个结点为右子树最左结点
{
pNode=pNode->right;
while(pNode->left!=NULL) //一直沿着指向左子结点的指针找到的叶子节点即为下一个节点
pNode=pNode->left;
return pNode;
}
while(pNode->next!=NULL)//无右子树时,返回父结点(向上查找,结点为左孩子的父结点)
{
TreeLinkNode *proot=pNode->next; //next指针指向节点的父节点
if(proot->left==pNode)
return proot;//返回父结点
pNode=pNode->next; //一直沿着父节点走
}
return NULL;
}
};
ღღღ
(14)剑指37.序列化二叉树【困难】(LC297)
知识点:string专门提供了一个名为c_str()的成员函数。
c_str函数的返回值是一个C风格的字符串,也就是说,函数的返回值是一个指针。见C++ primer P111
const_cast 见C++primer P145
请实现两个函数,分别用来序列化和反序列化二叉树。
示例:
你可以将以下二叉树:
1
/ \
2 3
/ \
4 5
序列化为 "[1,2,3,null,null,4,5]"
二叉树的序列化是指:把一棵二叉树按照某种遍历方式的结果以某种格式保存为字符串,从而使得内存中建立起来的二叉树可以持久保存。序列化可以基于先序、中序、后序、层序的二叉树遍历方式来进行修改,序列化的结果是一个字符串,序列化时通过 某种符号表示空节点(#),以 ! 表示一个结点值的结束(value!)。
二叉树的反序列化是指:根据某种遍历顺序得到的序列化字符串结果str,重构二叉树
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};
*/
class Solution {
public:
//序列化////////////////////////////////////////////////////////////////////
string sHelper(TreeNode *node)
{
if (node == NULL)
return "N";
return to_string(node->val) + "," +
sHelper(node->left) + "," +
sHelper(node->right);//按前序遍历来序列化
}
char* Serialize(TreeNode *root)
{
string s = sHelper(root);
char *ret = new char[s.length()+1];
strcpy(ret, const_cast<char*>(s.c_str())); //因为函数要求返回的是char* 所以需要类型的转换。
return ret;
}
或者这样转化类型:
/*
char* Serialize(TreeNode *root)
{
string s = sHelper(root); //得到string类型的串
int length = s.length(); //计算s的长度
char *ret = new char[length+1]; //+1是存放最后'\0'
// 把str流中转换为字符串返回
for(int i = 0; i < length; i++){
ret[i] = s[i];
}
ret[length] = '\0';
return ret;
*/
//反序列化////////////////////////////////////////////
TreeNode *dHelper(stringstream &ss)
{
string str;
getline(ss, str, ',');
if (str == "N")
return NULL;
else
{
TreeNode *node = new TreeNode(stoi(str));
node->left = dHelper(ss);
node->right = dHelper(ss);
return node;
}
}
TreeNode* Deserialize(char *str) {
stringstream ss(str);
return dHelper(ss);
}
};
不需要转换类型的代码:
class Codec {
public:
// Encodes a tree to a single string.
string serialize(TreeNode* root) { //因返回值为string类型,所以不需要转换类型
string s = sHelper(root);
return s;
}
string sHelper(TreeNode *node){
if (node == NULL)
return "N";
return to_string(node->val) + "," +
sHelper(node->left) + "," +
sHelper(node->right);//按前序遍历来序列化
}
// Decodes your encoded data to tree.
TreeNode* deserialize(string str) {
stringstream ss(str);
return dHelper(ss);
}
TreeNode *dHelper(stringstream &ss)
{
string str;
getline(ss, str, ',');
if (str == "N")
return NULL;
else
{
TreeNode *node = new TreeNode(stoi(str));
node->left = dHelper(ss);
node->right = dHelper(ss);
return node;
}
}
};
✍✍✍
重建二叉树知识点:
二叉树遍历的两个性质:
已知前序遍历和中序遍历,可以唯一确定一颗二叉树;
已知后序遍历和中序遍历,可以唯一确定一颗二叉树。
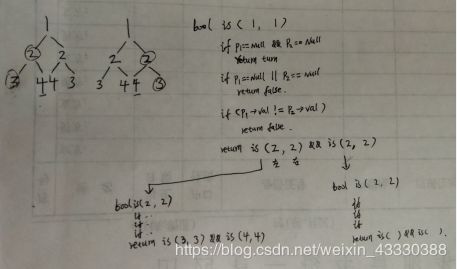
但是要注意了,已知前序和中序,是不能确定一颗二叉树的!
例1:
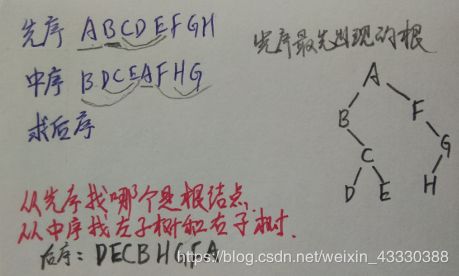
例2:

例3:

ღღღ
(15)剑指07.重建二叉树(已知前序和中序)【中等】(LC105)
根据一棵树的前序遍历与中序遍历构造二叉树。
注意:你可以假设树中没有重复的元素。
例如,给出
前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
返回如下的二叉树:
3
/ \
9 20
/ \
15 7
思路
虽然好理解,但是复杂度有点高!
思路:
由先序序列第一个pre[0]在中序序列中找到根节点位置gen
以gen为中心遍历
0~gen左子树
子中序序列:0~gen-1,放入vin_left[]
子先序序列:1~gen放入pre_left[],+1可以看图,因为头部有根节点
gen+1~vinlen为右子树
子中序序列:gen ~ vinlen-1放入vin_right[]
子先序序列:gen ~ vinlen-1放入pre_right[]
由先序序列pre[0]创建根节点
连接左子树,按照左子树子序列递归(pre_left[]和vin_left[])
连接右子树,按照右子树子序列递归(pre_right[]和vin_right[])
返回根节点
画图理解为什么这儿是i+1
pre_left.push_back(pre[i+1]);//先序第一个为根节点
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* buildTree(vector<int> pre, vector<int> vin) {
//int vinlen=vin.size();
if(pre.size()==0||vin.size()==0)
return NULL;
vector<int> pre_left, pre_right, vin_left, vin_right;
//创建根节点,根节点肯定是前序遍历的第一个数
TreeNode* head = new TreeNode(pre[0]);
//找到中序遍历根节点所在位置,存放于变量gen中
int gen=0;
for(int i=0;i<vin.size();i++){
if(vin[i]==pre[0]){
gen=i;
break;
}
}
//对于中序遍历,根节点左边的节点位于二叉树的左边,根节点右边的节点位于二叉树的右边
// 左子树
for(int i = 0; i < gen; i++){
vin_left.push_back(vin[i]);
pre_left.push_back(pre[i+1]);//先序第一个为根节点
}
// 右子树
for(int i = gen + 1; i < vin.size(); i++){
vin_right.push_back(vin[i]);
pre_right.push_back(pre[i]);
}
//递归,执行上述步骤,区分子树的左、右子子树,直到叶节点
head->left = buildTree(pre_left, vin_left);
head->right = buildTree(pre_right, vin_right);
return head;
}
};
ღღღ
(16)LC106.重建二叉树(已知中序和后序)【中等】
根据一棵树的中序遍历与后序遍历构造二叉树。
注意:你可以假设树中没有重复的元素。
例如,给出
中序遍历 inorder = [9,3,15,20,7]
后序遍历 postorder = [9,15,7,20,3]
返回如下的二叉树:
3
/ \
9 20
/ \
15 7
思路:与上题基本相同
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
if(inorder.size()==0 || postorder.size()==0) return NULL;
int len=postorder.size();//方便下面运用
TreeNode* head=new TreeNode(postorder[len-1]);
vector<int> in_left, post_left, in_right, post_right;
// 在中序序列中找到根节点位置
int gen=0;
for(int i=0; i<inorder.size(); i++){
if(inorder[i]==postorder[len-1]){
gen=i;
break;
}
}
for(int i=0; i<gen; i++){
in_left.push_back(inorder[i]);
post_left.push_back(postorder[i]);
}
for(int i=gen+1; i<inorder.size(); i++){
in_right.push_back(inorder[i]);
post_right.push_back(postorder[i-1]);
}
head->left=buildTree(in_left, post_left);
head->right=buildTree(in_right, post_right);
return head;
}
};
ღღღ
(17)98. 验证二叉搜索树【中等】
假设一个二叉搜索树具有如下特征:
节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
输入:
2
/ \
1 3
输出: true
法2,中序遍历后,判断排序前和排序后是否相同
自己发明的。好理解。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
bool isValidBST(TreeNode* root) {
vector<int> vec;
inorder(root,vec);
vector<int> pvec(vec); //保存原始序列为pvec
sort(vec.begin(),vec.end()); //对原始序列排序
for(int i=1; i<vec.size(); i++){//检查是否有重复元素
if(vec[i]==vec[i-1]) return false;
}
if(pvec==vec) return true;//排序前后对比
return false;
}
void inorder(TreeNode* root,vector<int>& vec){
if(root==NULL) return;
inorder(root->left,vec);
vec.push_back(root->val);
inorder(root->right,vec);
}
};
法1,思路:用中序遍历迭代法做,二叉查找树性质:中序遍历后,二叉查找树为升序排列
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
bool isValidBST(TreeNode* root) {
TreeNode* pre=NULL;
stack<TreeNode*> s;
TreeNode *p = root;
while(p || !s.empty()){
if(p){ //当左结点不为空时
s.push(p); //入栈
p = p->left; //指向下一个左结点
}
else{ //当左结点为空时
p = s.top();
if(pre!=NULL && p->val <= pre->val) return false;//看是否为升序
pre=p; //pre实际上是指向了前一个数
s.pop(); //出栈
p = p->right; //指向右结点
}
}
return true;
}
};
//参考 非迭代中序遍历:
while(p || !s.empty()){
if(p){ //当左结点不为空时
s.push(p); //入栈
p = p->left; //指向下一个左结点
}
else{ //当左结点为空时
p = s.top();
path.push_back(p->val); //访问栈顶元素(父结点)
s.pop(); //出栈
p = p->right; //指向右结点
}
}
ღღღ
(18)剑指36. 二叉搜索树与双向链表【中等】(LC426)
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点,只能调整树中节点指针的指向。
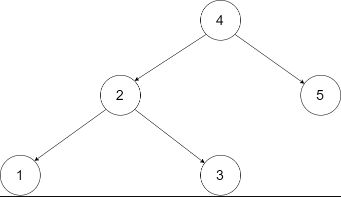
转化后变为:
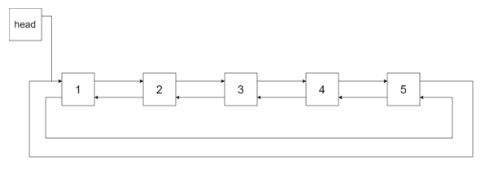
思路:先中序遍历,再用2个for循环摆好指针的位置。
对二叉搜索树进行中序遍历后,就相当于排序了。
/*
// Definition for a Node.
class Node {
public:
int val;
Node* left;
Node* right;
Node() {}
Node(int _val) {
val = _val;
left = NULL;
right = NULL;
}
Node(int _val, Node* _left, Node* _right) {
val = _val;
left = _left;
right = _right;
}
};
*/
class Solution {
public:
Node* treeToDoublyList(Node* pRoot) {
if (nullptr == pRoot){
return nullptr;
}
tranverse(pRoot);
return adjustTree();
}
vector<Node*> nodes;
void tranverse(Node* pRoot) {//中序遍历
if (nullptr == pRoot)
return;
tranverse(pRoot->left);
nodes.push_back(pRoot);
tranverse(pRoot->right);
}
Node* adjustTree() {
for (int i = 0; i < nodes.size() - 1; ++i)
nodes[i]->right = nodes[i+1]; //因为一个结点只有左指针和右指针而没有next指针。
nodes[nodes.size()-1]->right = nodes[0];//最后一个节点的右指向第一个节点
//nodes[nodes.size()-1]->right = nullptr; //如果题目只要求转化为双向链表,而不是循环双向链表
for (int i = nodes.size() - 1; i > 0; --i)
nodes[i]->left = nodes[i-1];
nodes[0]->left =nodes[nodes.size()-1] ;//第一个节点左指向租后一个节点
//nodes[0]->left = nullptr; //如果题目只要求转化为双向链表,而不是循环双向链表
return nodes[0];//返回头节点
}
};
ღღღ
(19)剑指33. 二叉搜索树的后序遍历序列【中等】
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true,否则返回 false。假设输入的数组的任意两个数字都互不相同。
参考以下这颗二叉搜索树:
5
/ \
2 6
/ \
1 3
示例 1:
输入: [1,6,3,2,5]
输出: false
示例 2:
输入: [1,3,2,6,5]
输出: true
思路:解题思路
后序遍历最后节点为根节点
二叉搜索树左子树都小于根节点,右子树都大于根节点
因此可以找出左子树和右子树理论分界处进行判断,再左右子树递归判断是否为二叉搜索树
/*
后序遍历序列规律:最后一个元素为根结点,前面左半部分为左子树,右半部分为右子树
BST规律:对任意结点,左结点<根结点<右结点的
根据这两个规律进行判断
*/
class Solution {
public:
bool VerifySquenceOfBST(vector<int> sequence) {
if(sequence.empty()) return false;
return verify(sequence, 0, sequence.size()-1);
}
private:
bool verify(vector<int>& a, int begin, int end){
if(begin >= end) return true; //不理解为什么>=
//只有一个元素了,其没有左右子树,没有判断的必要,故返回true
int root = a[end]; //根结点的值
//计算左子树序列的长度(左子树中结点值均小于根结点值)
int i = begin;
for(; i<end; i++){//注意这里最多扫描到倒数第二个元素(最后一个元素为根结点)
if(a[i] > root) break; //一旦大于根结点就退出
}//退出时,i即为左子树序列的长度
//判断右子树序列是否满足大于根结点的规律
for(int j = i; j<end; j++){
if(a[j] < root) return false; //若右子树不满足规律,则返回false
}
//判断左子树和右子树是否为二叉搜索树
return verify(a, begin, i-1) && verify(a, i, end-1);
}
};
同上
class Solution {
public:
bool verifyPostorder(vector<int>& postorder) {
if(postorder.size() ==0) return true;
return isPostorder(postorder, 0, postorder.size()-1);
}
//后序遍历最后节点为根节点,二叉搜索树左子树都小于根节点,右子树都大于根节点,因此可以找出左子树和右子树理论分界处进行判断,再左右子树递归判断
bool isPostorder(vector<int>& postorder, int start, int end){
if(start >= end) return true;
int i=start;
//while(postorder[i] < postorder[end]) //左子树
// i++;
for(; i<end;i++){ //注意:end已经是下标了,所以不是end-1
if(postorder[i]>postorder[end]) break;
}
int bound = i; //左右子树理论分界点
for(; i<end; i++) //右子树应该小于根节点,否则不是二叉搜索树
{
if(postorder[i] < postorder[end]) return false;
}
return isPostorder(postorder, start, bound-1) && isPostorder(postorder, bound, end-1); //递归判断左右子树
}
};
书上的方法,太复杂!
class Solution {
public:
bool VerifySquenceOfBST(vector<int> sequence) {
if(sequence.empty())
return false;
int length=sequence.size();
int root=sequence[length-1];
//找左子树
int i=0;
for(;i<length-1;++i)
{
if(sequence[i]>root)
break;
}
//找右子树
int j=i;
for(;j<length-1;++j)
{
if(sequence[j]<root)
return false;
}
//判断左子树是不是二叉搜索树
bool left=true;
vector<int> sequence1;
for(int m=0;m<i;++m)
{
sequence1.push_back(sequence[m]);
}
if(i>0)
left=VerifySquenceOfBST(sequence1);
//判断右子树是不是二叉搜索树
bool right=true;
vector<int> sequence2;
for(int m=0;m<length-i-1;++m)
{
sequence2.push_back(sequence[m+i]);
}
if(i<length-1)
right=VerifySquenceOfBST(sequence2);
return (left&&right);
}
};
ღღღ
(20)剑指54. 二叉搜索树的第k大节点
给定一棵二叉搜索树,请找出其中第k大的节点。
示例 1:
输入: root = [3,1,4,null,2], k = 1
3
/ \
1 4
\
2
输出: 4
示例 2:
输入: root = [5,3,6,2,4,null,null,1], k = 3
5
/ \
3 6
/ \
2 4
/
1
输出: 4
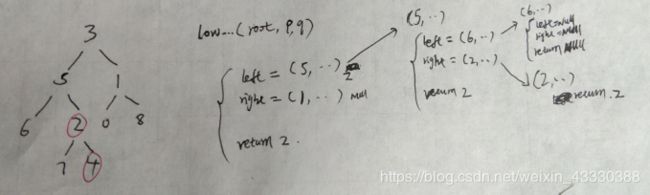
第k大节点,意思是从大的开始数,所以中序遍历完之后从后面开始数。具体看题目示例吧。
注意函数要求的是节点本身,还是节点的值。对应中序遍历 vec.push_back(root); 还是vec.push_back(root->val);
思路:中序遍历完之后直接从后面开始取值。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
int kthLargest(TreeNode* root, int k) {
if(root==NULL || k<=0) return NULL;
vector<int> vec;
inorder(root, vec);
if(k>vec.size()) return NULL;
return vec[vec.size()-k];
//reverse(vec.begin(),vec.end());
//return vec[k-1];
}
void inorder(TreeNode* root , vector<int>& vec){
if(root==NULL) return;
inorder(root->left,vec);
vec.push_back(root->val);
inorder(root->right,vec);
}
};
ღღღ
(21)230. 二叉搜索树中第K小的元素【中等】
方法一:中序遍历递归法
BST中序遍历之后为从小到大排列
中序遍历递归法,不是最优的,因为是遍历完之后在给出的结果(可用迭代法进行改进)
注:可在递归中加入判断进行减枝
class Solution {
public:
int kthSmallest(TreeNode* pRoot, int k) {
if(pRoot==NULL||k<=0) return NULL;
vector<int> vec;
Inorder(pRoot,vec);
if(k>vec.size())
return NULL;
return vec[k-1];
}
//中序遍历,将节点依次压入vector中
void Inorder(TreeNode* pRoot,vector<int>& vec)
{
if(pRoot==NULL) return;
Inorder(pRoot->left,vec);
vec.push_back(pRoot->val);
Inorder(pRoot->right,vec);
}
};
方法二:中序遍历迭代法
在遍历的过程中统计数量
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
int kthSmallest(TreeNode* root, int k) {
int n=0;
stack<TreeNode*> s;
TreeNode *p = root;
while(p || !s.empty()){
if(p){ //当左结点不为空时
s.push(p); //入栈
p = p->left; //指向下一个左结点
}
else{ //当左结点为空时
p = s.top();
n++; //统计数目(遍历到了要访问的父结点)
if(n==k) return p->val;
s.pop(); //出栈
p = p->right; //指向右结点
}
}
return 0;
}
};
ღღღ
(22)剑指68 - I. 二叉搜索树的最近公共祖先(LC235)
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
思路
如果根节点的值大于p和q之间的较大值,说明p和q都在左子树中,那么此时我们就进入根节点的左子节点继续递归,如果根节点小于p和q之间的较小值,说明p和q都在右子树中,那么此时我们就进入根节点的右子节点继续递归,如果都不是,则说明当前根节点就是最小共同父节点,直接返回即可
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root==NULL) return NULL;
if(p->val > root->val && q->val > root->val){//如果p,q在当前结点右子树,则对右子树遍历
return lowestCommonAncestor(root->right,p,q);
}
else if(p->val < root->val && q->val < root->val){//如果p,q在当前结点左子树,则对左子树遍历
return lowestCommonAncestor(root->left,p,q);
}
else return root; //如果当前结点在p,q之间,则为最低公共父结点
}
};
ღღღ
(23)剑指68 - II. 二叉树的最近公共祖先(LC236)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
// LCA(Least Common Ancestor)问题
if (root == NULL) {//当遍历到叶结点后就会返回null
return NULL;
}
if (root == p || root == q) {//直接返回公共祖先
return root;
}
TreeNode* left = lowestCommonAncestor(root->left, p, q);//返回的结点进行保存,可能是null
TreeNode* right = lowestCommonAncestor(root->right, p, q);
if (left != NULL && right != NULL) {
return root;
} else if (left != NULL) {
return left;
} else if (right != NULL) {
return right;
}
return NULL;
}
};
(24)108. 将有序数组转换为二叉搜索树
深度优先搜索/递归/分治
1、固定一个left和right变量,取mid作为root节点。
2、递归得到root的左子树root的右子树。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* sortedArrayToBST(vector<int>& nums) {
return sortedArrayToBST(nums, 0, nums.size() - 1);//注意索引从0开始
}
TreeNode* sortedArrayToBST(vector<int>& nums, int l, int r) {
if (r < l) return NULL;//递归子函数的出口(不能取等号,因为单个元素也要分配空间)
//int mid = l + (r-l)/2;
int mid=(l+r)>>1;
TreeNode* root = new TreeNode(nums[mid]); //构建根结点
root->left = sortedArrayToBST(nums, l, mid - 1);//构建左子树
root->right = sortedArrayToBST(nums, mid + 1, r);//构建右子树
return root;//递归原始母函数的出口,返回最顶层的根结点指针
}
};