李宏毅机器学习（一）

一、机器学习三步骤：

Step1: Define a set of function

Model：定义一些函数$f_1{f}_2...$

Step2: Goodness of function

使用训练数据，根据输入输出判断函数的好坏。

Step3: Pick the best function

通过Testing挑选出最好的函数。

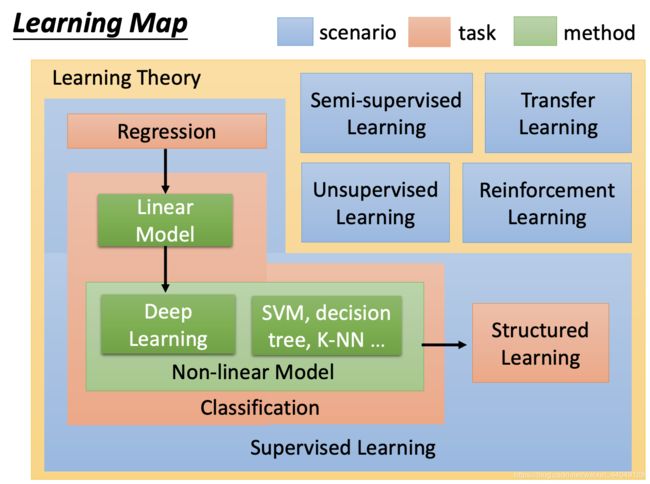
二、Learning Map：

scenario(学习情境) task(要解决的问题) method(解决方法)

1、Supervised Learning(监督学习)

（1）Regression（回归）

**定义：**The output of the target function $f$ is “scalar”

**例子：**预测PM2.5

（2）Classification（分类）

• Binary Classification

  垃圾邮件分类：输入训练数据，告诉函数邮件是否是垃圾邮件。最后能自己判断邮件情况。

• Multi-class Classification

  文档分类：输入训练数据，对数据进行多个分类：政治、体育、财经…….

（3）Struct Learning(结构化预测)

​ ------Beyond Classification

输出的是有结构性的复杂的东西。例如语音识别，根据声音信号的输入输出文字；机器翻译，根据中文输出，输出英文；人脸识别，识别出每个人脸来。

1. Non-Linear Model(非线性模型)

主要是Deep Learning、SVM、决策树、K-NN。这种模型的函数十分复杂，可以用来进行图像分类问题。

2. Linear Model(线性模型)

(4) Training Data

数据输入和输出之间有什么联系，输出（output）是数据的标签（label）。大量的label比较难获取。

2、Unsupervised Learning(非监督学习)

Machine Reading(机器阅读)：机器通过阅读大量的文章，从而学习词语的意思。只有输入数据，但是没有输出。

Machine Drawing(机器绘画)：训练数据是一堆图片，但是没有做标记。

3、Semi-supervised Learning

识别猫狗，有一些数据是给猫图数据标记为猫、狗图数据标记为狗。但是一堆没有给猫狗图做标签的数据，对学习也有帮助。

4、Transfer Learning：

识别猫狗，一些标记了的数据，另外一些是标记或者没标记的其它不相关的数据，也能够带来帮助。

5、Reinforcement Learning(强化学习)

（1 ）Supervised v.s. Reinforcement

Supervised：按照人为监督机器进行学习。

Reinforcement：不会告诉机器怎么做，只会给机器学习后的结果做评分。

1. Regression(回归)

(1) 例子

• 股票预测：找一个函数，输入股票数据，得出明天的股票指数。
• 自动驾驶汽车：找一个函数，根据情境，调整方向盘角度。
• 推荐系统：找一个函数，输入使用者A和商品B，得出使用者A购买B的可能性。

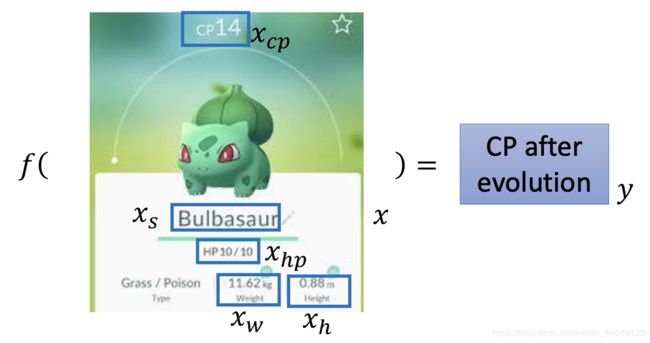
(2) 预测宝可梦的CP（Combat Power）值

1. 找一个函数，输入宝可梦，得出宝可梦进化后的CP值。
   

Step 1：Model（function set）
$$y=b+w.x_{cp}\text{\hspace{1em}(1)}$$
其中$w$和$b$都是参数可以是任意值，$x_{cp}$是预测之前的CP值，$y$是预测之后的CP值。

Linear model(线性方程)：$y=b+\sum w_i{x}_i$
($x_i$是输入的一种属性，$w_i$是weight权重，$b$表示bias偏置值)

Step 2：Goodness of Function

训练数据：10个宝可梦.$(x^1,{\hat{y}}^1)$、$(x^2,{\hat{y}}^2)$、$(x^3,{\hat{y}}^3)$…$x^{10},{\hat{y}}^{10})$
https://www.openintro.org/stat/data?data=pokemon

通过训练数据可以定义一个函数的好坏：
$$L(f)=L(w,b)=\sum _{n=1}^{10}({\hat{y}}^n-(b+w.x_{cp}^n){)}^2\text{\hspace{1em}(2)}$$
(真正的数值减去当前函数预测的数值再取平方，就是估测的误差，再把10个数据误差加起来)

使用Loss function $L$，输入是一个函数，输出是输入函数的不好的程度，然后选择出一个最好的函数。穷举所有的$wb$，然后选出使损失函数值为最小的，就找到了最好的函数。
$f^{\ast }=argminL(f)$
$w^{\ast },b^{\ast }=argminL(w,b)$
$argmin{\sum }_{n=1}^{10}({\hat{y}}^n-(b+w.x_{cp}^n)$
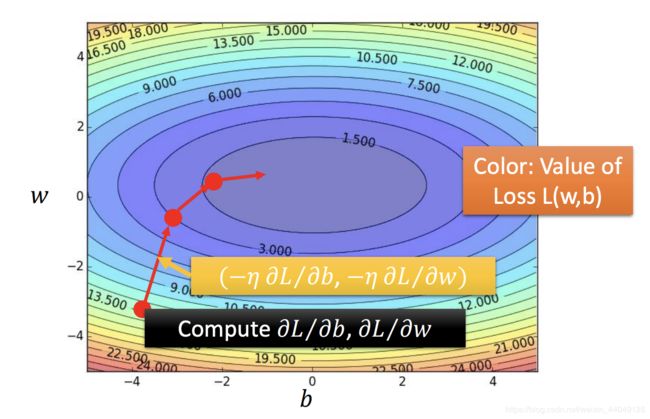
Step 3：Gradient Descent（梯度下降）

通过一个参数$w$，考虑损失函数：

• 随机选取一个初始值$w^0$
• 计算$\frac{dL}{dw}{|}_w=w^0$，如果斜率是负的，那么增加w的值；如果斜率是正的，那么增加w的值。
• 计算新的权重$w^1=w^0-\eta \frac{dL}{dw}{|}_{w=w_0}$，其中的$\eta$就是学习率"learning rata"。
• 重复步骤，计算$w^2=w^1-\eta \frac{dL}{dw}{|}_{w=w_1}$
• 经过多次迭代
• 遇到鞍点（局部最优点而非全局最优点），可能会导致梯度停止更新。

经过多次迭代后，能够找到局部最优和全局最优。

上面讨论的是一个参数的问题，下面讨论两个参数$w$和$b$：

• 随机选取两个参数$w^0$和$b^0$
• 计算两个偏微分：$\frac{dL}{dw}{|}_{w=w^0}$, $\frac{dL}{db}{|}_{w=w^0,b=b^0}$
• $w^1=w^0-\eta \frac{dL}{dw}{|}_{w=w^0,b=b^0}$, $b^1=b^0-\eta \frac{dL}{db}{|}_{w=w^0,b=b^0}$
• 再计算两个偏微分：$\frac{dL}{dw}{|}_{w=w^1,b=b^1}$, $\frac{dL}{db}{|}_{w=w^1,b=b^1}$
• 更新参数，$w^2=w^1-\eta \frac{dL}{dw}{|}_{w=w^1,b=b^1}$, $b^2=b^1-\eta \frac{dL}{db}{|}_{w=w^1,b=b^1}$

下面使用一张图说明怎么调整包含两个参数的值：

首先，随机选择一个(w, b)，然后计算L对w和b的偏微分,根据结果调整梯度大小。下面展开L对w和b的偏微分：

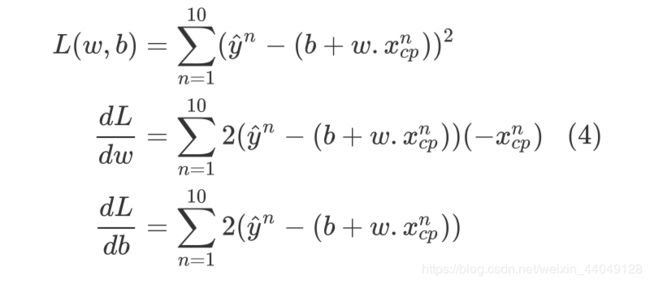
Result
经训练，$y=b+w.x_{cp}$的结果：
$$\begin{gathered} b=-188.4 \\ w=2.7 \\ a\_e=31.9 \end{gathered}$$
但是真正关心的average—error在于在新的宝可梦上的准确率。在新的10只宝可梦数据测试后，$a_e=35.0>31.9$。如果要函数想要做得更好，应该再设计一下model：
$$y=b+w_1.x_{cp}+w_2.(x_{cp}{)}^2\text{\hspace{1em}(5)}$$
经过训练之后，结果如下：
$$\begin{gathered} b=-10.3 \\ {w}_1=1.0 \\ {w}_2=2.7\times 10^{-3} \\ a\_e=15.4 \end{gathered}$$
但是测试的average_error是18.4。此时average_error已经很低了，但是如果想要更好的function，需要再增加$x$的次方数：
$$y=b+w_1.x_{cp}+w_2.(x_{cp}{)}^2+w_3.(x_{cp}{)}^3\text{\hspace{1em}(5)}$$
经过训练之后，结果如下：
$$\begin{gathered} b=-6.4 \\ {w}_1=0.66 \\ {w}_2=4.3\times 10^{-3} \\ {w}_2=-1.8\times 10^{-6} \\ a\_e=15.3 \end{gathered}$$
测试的average_error是18.1。最好的函数或许是一个更加复杂的函数？
$$y=b+w_1.x_{cp}+w_2.(x_{cp}{)}^2+w_3.(x_{cp}{)}^3+w_4.(x_{cp}{)}^4\text{\hspace{1em}(6)}$$
训练之后的$a\_e=14.9$,但是测试数据上的结果是$a_e=28.8$,在新数据上拟合更差了。再加次方数，在测试数据上更糟糕。

因此，可以得出规律：model更复杂，在训练数据上的误差值就越低，但是在测试数据上不一样，误差值会逐渐降低之后暴增。

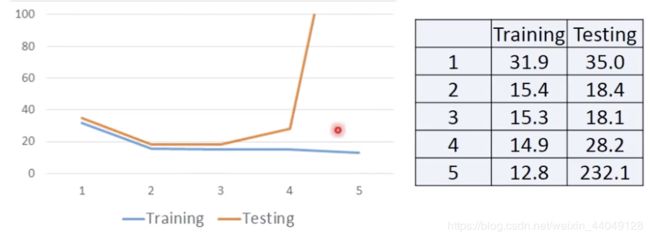
这种情况就是"Over fitting"，即为过拟合，不是模型越复杂越好，应该选择一个合适的模型。

或许存在一些隐藏因素影响进化后的CP值？

Back to Step 1:

重新设计Model(考虑物种因素)：

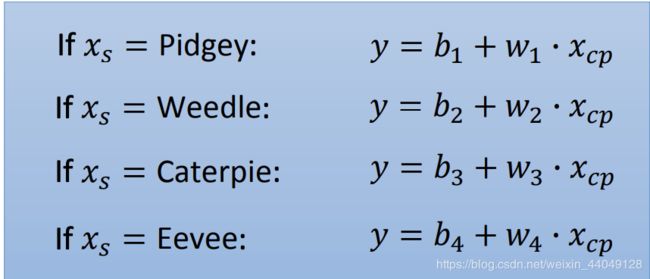
除去if，写出函数形式：

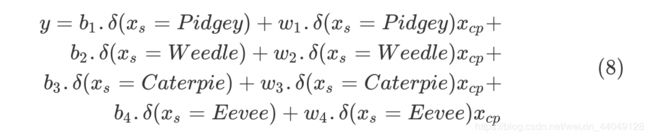
如果输入数据是某种宝可梦，该宝可梦对应的$\delta (x_s)$是1，其余的是0。

考虑到种类之后，在训练数据上的$a\_e=3.8$，在测试数据上$a\_e=14.3$。如果还要完善，则把相关的影响因素全部加入到model中：考虑进化前CP值（$x_{cp}$）、种类($x_s$)、HP值($x_{hp}$)、高度($x_h$)、体重($x_w$)。

用这个Model在训练数据上的$a\_e=1.9$，但是在测试数据上是$102.3$。

Back to Step 2：Regularization

给Loss function加入正则化：
$$\begin{gathered} y=b+\sum w_i{x}_i \\ L=\sum _n({\hat{y}}^n-(b+\sum w_i{x}_i){)}^2+\lambda \sum (w_i{)}^2\text{\hspace{1em}(9)} \end{gathered}$$
根据公式(9)，可以看出损失函数需要的更优结果是$|w_i|$更小，因此函数会更加平滑，对输入数据更不敏感，变化越小，更不容易被噪音noise影响到，能防止在新数据上偏差大，得到一个比较好的结果。但是也不能太平滑，还是需要调整一个合适的$\lambda$，如下图所示：

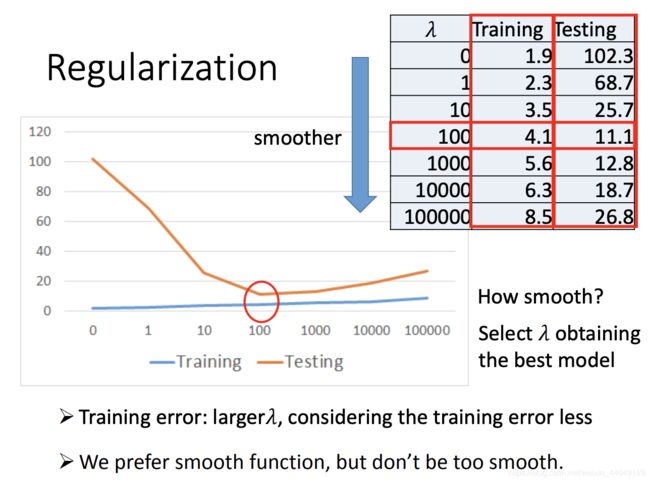
正则化为什么不考虑b——因为函数的平滑与否，跟它没关系。

相关学习

1 中心极限定理

（1）定义

• 样本的平均值约等于总体的平均值。
• 不管总体是什么分布，任意一个总体的样本平均值都会围绕在总体的整体平均值周围，并且呈正态分布。

(2) 理解

1. 随机抽取1个样本，样本大小为100，求该样本的平均值。(根据经验，样本大小必须达到30，中心极限定理才保证成立)
2. 将第1步样本抽取的工作重复再三，不断地从总体随机抽取样本，例如我抽取了5个样本，每个大小为100，并计算出每个样本的平均值，那么5个样本，就会有5个平均值。因此，样本数量为5。
3. 根据中心极限定理，这些样本平均值中的绝大部分都极为接近总体的平均值。有一些会稍高一点，有一些会稍低一点，只有极少数的样本平均值大大高于或低于群体平均值。
4. 中心极限定理告诉我们，不论所研究的群体是怎样分布的，这些样本平均值会在总体平均值周围呈现一个正态分布。

(3) 样本估计整体

• 标准差：数据集中数值与平均值的偏离程度。

• 一般样本数据更加紧密聚集在均值周围，所以样本的标准差是要小于总体标准差。

• 所以，为了更好的用样本估计总体的标准差，统计学家就将标准差的公式做了像下面公式中这样的改造。

  数据集标准差$\sigma$：
  $$\sigma =\sqrt{\frac{\sum (x-\mu {)}^2}{n}}\text{\hspace{1em}(1)}$$
  样本标准差$s$：
  $$s=\sqrt{\frac{\sum (x-\mu {)}^2}{n-1}}\text{\hspace{1em}(2)}$$

• 原来的标准差公式是除以$n$，为了用样本估计总体标准差，现在是除以$n-1$。这样就是的标准略大。

• 如果只是想计算一个数据集的标准差，那么就除以n；如果想把这个数据集当成一个样本，用这个样本来估计出总体的标准差，那么就除以n-1的标准差公式。

(4) 标准误差

• 定义：标准误差其实也是标准差，只不过它是所有样本平均值的标准差。怎么理解呢？其实就是你选取多个样本，对每个样本求平均值，每个平均值又组成了一个新的数据集，然后对这些平均值计算标准差，就是标准误差。概括成一句话：求样本平均值的标准差就是标准误差。

• 作用：用来衡量样本平均值的波动大小。

• 计算公式：
  $$SE=\frac{s}{\sqrt{n}}\text{\hspace{1em}(3)}$$
  标准误差$SE$等于总体标准差除以$n$的开，可以用样本来估计出总体标准差的公式$s$。

(5) 中心极限定理的作用

1. 在没有办法得到总体全部数据的情况下，我们可以用样本来估计总体
2. 根据总体的平均值和标准差，判断某个样本是否属于总体

(6) 中心极限定理的代码模拟

本代码来源:https://github.com/sijichun/MathStatsCode/blob/master/notebook_python/LLN_CLT.ipynb

import numpy as np
from numpy import random as nprd

def sampling(N):
    ## 产生一组样本，以0.5的概率为z+3，0.5的概率为z-3，其中z~N(0,1)
    d = nprd.rand(N)<0.5
    z=nprd.randn(N)
    x=np.array([z[i]+3 if d[i] else z[i]-3 for i in range(N)])
    return x

N=[2,3,4,10,100,1000] # sample size
M=2000
MEANS=[]
for n in N:
    mean_x=np.zeros(M)
    for i in range(M):
        x=sampling(n)
        mean_x[i]=np.mean(x)/np.sqrt(10/n) ## 标准化，因为var(x)=10
    MEANS.append(mean_x)

## 导入matplotlib
import matplotlib.pyplot as plt
import matplotlib.mlab as mlab
## 使图形直接插入到jupyter中
%matplotlib inline
# 设定图像大小
plt.rcParams['figure.figsize'] = (10.0, 8.0)

x=sampling(1000)
plt.xlabel('x')
plt.ylabel('Density')
plt.title('Histogram of Mixed Normal')
plt.hist(x,bins=30,normed=1) ## histgram
plt.show() ## 画图

## 均值
ax1 = plt.subplot(2,3,1)
ax2 = plt.subplot(2,3,2)
ax3 = plt.subplot(2,3,3)
ax4 = plt.subplot(2,3,4)
ax5 = plt.subplot(2,3,5)
ax6 = plt.subplot(2,3,6)

## normal density
x=np.linspace(-3,3,100)
d=[1.0/np.sqrt(2*np.pi)*np.exp(-i**2/2) for i in x]

def plot_density(ax,data,N):
    ax.hist(data,bins=30,normed=1) ## histgram
    ax.plot(x,d)
    ax.set_title(r'Histogram of $\bar{x}$:N=%d' % N)

plot_density(ax1,MEANS[0],N[0])
plot_density(ax2,MEANS[1],N[1])
plot_density(ax3,MEANS[2],N[2])
plot_density(ax4,MEANS[3],N[3])
plot_density(ax5,MEANS[4],N[4])
plot_density(ax6,MEANS[5],N[5])


plt.show() ## 画图

2 正态分布

• 定义：若随机变量$X$服从一个位置参数为$\mu$，尺度参数为$\sigma$的正态分布，记为：
  $$\begin{gathered} X\sim N(\mu ,{\sigma }^2) \\ f(x)=\frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}\text{\hspace{1em}(4)} \end{gathered}$$

• 正态分布中一些值得注意的量：

  • 密度函数关于平均值对称
  • 平均值与它的众数以及中位数是同一数值。
  • 函数曲线下68.268949%的面积在平均数左右的一个标准差范围内。
  • 95.449974%的面积在平均数左右两个标准差$2\sigma$的范围内。
  • 99.730020%的面积在平均数左右三个标准差$3\sigma$的范围内。
  • 99.993666%的面积在平均数左右四个标准差$4\sigma$的范围内。
  • 函数曲线的拐点为离平均数一个标准差距离的位置。

3 最大似然估计

• 定义：利用已知的样本结果信息，反推最具有可能（最大概率）导致这些样本结果出现的模型参数值。提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”的方法。
• 似然函数：对于函数$P(x|\theta )$，输入$x$表示某一个具体的数据，$\theta$表示模型的参数。如果$\theta$是已知确定的，$x$是变量，这个函数叫做概率函数(probability function)，它描述对于不同的样本点$x$，其出现概率是多少。如果$x$是已知确定的，$\theta$是变量，这个函数叫做似然函数(likelihood function)， 它描述对于不同的模型参数，出现$x$这个样本点的概率是多少。
• 最大似然估计（MLE）：是求参数$\theta$, 使似然函数$P(x_0|\theta )$最大。
• 例子：假如有一个罐子，里面有黑白两种颜色的球，数目多少不知，两种颜色的比例也不知。想知道罐中白球和黑球的比例，但我们不能把罐中的球全部拿出来数。现在我们可以每次任意从已经摇匀的罐中拿一个球出来，记录球的颜色，然后把拿出来的球再放回罐中。这个过程可以重复，我们可以用记录的球的颜色来估计罐中黑白球的比例。假如在前面的一百次重复记录中，有七十次是白球，请问罐中白球所占的比例最有可能是多少？
  很明显是70%。
• 解释：设例子中100次抽样的结果概率表示为P(样本结果|Model) = $p^{70}.(1-p{)}^{30}$,其中$p$表示白球的比例。要求的是模型的参数，也就是求式中的$p$。$p$是可以有无数种分布的，例如$p=50\%$，此时结果$p^{70}.(1-p{)}^{30}=7.8\ast 10^{-31}$ 结果是；当$p=70$，$p^{70}.(1-p{)}^{30}=2.95\ast 10^{-27}$.从这里就能看出，极大似然估计是按照让这个样本结果出现的可能性最大的方法选择Model参数值。

4 损失函数与凸函数之间的关系

在线性回归中，损失函数$L$一定是凸函数。但是其它函数可能是非凸函数，这会导致损失函数存在局部最优解，导致无法找到全局最优解。

5 泰勒展开

• 定义：若函数$f(x)$在包含$x_0$的某个闭区间$[a,b]$上具有n阶导数，且在开区间$(a,b)$上具有（n+1）阶导数，则对闭区间$[a,b]$上任意一点$x$，成立下式：
  $$f(x)=f(x_0)+\frac{f^{‘}(x_0)}{1!}(x-x_0)+\frac{f^{‘‘}{x}_0)}{2!}(x-x_0{)}^2+...+\frac{f^{(n)}(x_0)}{n!}(x-x_0{)}^n+R_n(x)$$

6 L2-Norm，L1-Norm，L0-Norm

• 这三者是机器学习中的正则化，常用来：1）保证模型尽可能的简单，避免过拟合；2）约束模型特性，加入一些先验知识，例如稀疏、低秩等。L1表示曼哈顿距离，L2表示欧式距离。

• L0范数是指向量中非零元素的个数，如果用L0规则化一个参数矩阵$W$，就是希望$W$中大部分元素是零，实现稀疏。L1范数是指向量中各个元素的绝对值之和，也叫”系数规则算子（Lasso regularization）“。L1范数也可以实现稀疏，通过将无用特征对应的参数$W$置为零实现。L0和L1都可以实现稀疏化，不过一般选用L1而不用L0。L2范数是指向量各元素的平方和然后开方，用在回归模型中也称为岭回归（Ridge regression）。L2避免过拟合的原理是：让L2范数的规则项$||W|{|}_2$ 尽可能小，可以使得W每个元素都很小，接近于零，但是与L1不同的是，不会等于0；这样得到的模型抗干扰能力强，参数很小时，即使样本数据$x$发生很大的变化，模型预测值$y$的变化也会很有限。

7 正则化及其推导

1）L1正则化

大部分的正则化方法是在经验风险或者经验损失$L_{emp}$（emprirical loss）上加上一个结构化风险，我们的结构化风险用参数范数惩罚$\Omega (\theta )$，用来限制模型的学习能力、通过防止过拟合来提高泛化能力。所以总的损失函数（也叫目标函数）为：
$$J(\theta ;X,y)=L_{emp}(\theta ;X,y)+\alpha \Omega (\theta )\text{\hspace{1em}(1.1)}$$
其中$X$是输入数据，$y$是标签，$\theta$是参数，$\alpha \in [0,+\infty ]$是用来调整参数范数惩罚与经验损失的相对贡献的超参数，当$\alpha =0$时表示没有正则化，$\alpha$越大对应该的正则化惩罚就越大。对于L1正则化，我们有：
$$\Omega (\theta )=\Vert w{\Vert }_1\text{\hspace{1em}(1.2)}$$

根据上两式，可以推导出L1正则化的目标函数：
$$J(w;X,y)=L_{emp}(w;X,y)+\alpha \Vert w{\Vert }_1\text{\hspace{1em}(1.3)}$$
我们的目的是求得使目标函数取最小值的$w^{\ast }$，上式对$w$求导可得：
$${\nabla }_{w}J(w;X,y)={\nabla }_w{L}_{emp}(w;X,y)+\alpha \cdot sign(w)\text{\hspace{1em}(1.4)}$$
其中若$w>0$，则$sign(w)=1$；若$w<0$，则$sign(w)=-1$；若$w=0$，则$sign(w)=0$。当$\alpha =0$，假设我们得到最优的目标解是$w^{\ast }$，用泰勒公式在$w^{\ast }$处展开可以得到：
$$J(w;X,y)=J(w^{\ast };X,y)+\frac{1}{2}(w-w^{\ast })H(w-w^{\ast })\text{\hspace{1em}(1.5)}$$
其中$H$是关于$w$的Hessian矩阵，为了得到更直观的解，我们简化H，假设H是对角矩阵，则有：
$$H=diag([H_{1,1},H_{2,2}...H_{n,n}])\text{\hspace{1em}(1.6)}$$
将上式代入到式(1.3)中可以得到，我们简化后的目标函数可以写成这样：
$$J(w;X,y)=J(w^{\ast };X,y)+\sum _i[\frac{1}{2}{H}_{i,i}(w_i-w_i^{\ast }{)}^2+{\alpha }_i|w_i|]\text{\hspace{1em}(1.7)}$$
从上式可以看出，w各个方向的导数是不相关的，所以可以分别独立求导并使之为0，可得：
$$H_{i,i}(w_i-w_i^{\ast })+\alpha \cdot sign(w_i)=0\text{\hspace{1em}(1.8)}$$
我们先直接给出上式的解，再来看推导过程：
$$w_i=sign(w^{\ast })max\{|w_i^{\ast }|-{\frac{\alpha }{H}}_{i,i},0\}\text{\hspace{1em}(1.9)}$$
从式(1.7)与式(1.8)可以得到两点：

1. 可以看到式(1.7)中的二次函数是关于$w^{\ast }$对称的，所以若要使式(1.7)最小，那么必有：$|w_i|<|w^{\ast }|$，因为在二次函数值不变的程序下，这样可以使得$\alpha |w_i|$更小。

2. $sign(w_i)=sign(w_i^{\ast })$或$w_1=0$，因为在$\alpha |w_i|$不变的情况下，

   $sign(w_i)=sign(w_i^{\ast })$或$w_i=0$可以使式(1.7)更小。

由式(1.8)与上述的第2点，可以得到：
$$\begin{gathered} 0=H_{i,i}(w_i-w_i^{\ast })+\alpha \cdot sign(w_i^{\ast }) \\ {w}_i=w_i^{\ast }-{\frac{\alpha }{H}}_{i,i}sign(w_i^{\ast }) \\ {w}_i=sign(w_i^{\ast })|w_i^{\ast }|-\alpha H_{i,i}sign(w^{\ast }i) \\ =sign(w_i^{\ast })(|w_i^{\ast }|-{\frac{\alpha }{H}}_{i,i})\text{\hspace{1em}(1.10)} \end{gathered}$$
我们再来看一下第2点：$sign(w_i)=sign(w_i^{\ast })$或$w_1=0$，若$|w_i^{\ast }|<{\frac{\alpha }{H}}_{i,i}$，那么有$sign(w_i)̸=sign(w^{\ast }i)$，所以这时有$w_1=0$，由于可以直接得到解式(1.9)。从这个解可以得到两个可能的结果：

1. 若$|w^{\ast }i|\le \alpha H_{i,i}$，正则化后目标中的$w_i$的最优解是$w_i=0$。因为这个方向上$L_{emp}(w;X,y)$的影响被正则化的抵消了。
2. 若$|w_i^{\ast }|>{\frac{\alpha }{H}}_{i,i}$，正则化不会推最优解推向0，而是在这个方面上向原点移动了αHi,iαHi,i的距离。

8 L1-Norm代替L0-Norm

原因包括：

（1）L0范数很难优化求解（NP难）；

（2）L1是L0的最优凸近似，比L0更容易优化求解。

9 为什么只对w/Θ做限制，不对b做限制

因为影响梯度大小的只有$w$值，而与$b$无关。