GNN—图网络入门

最近的图深度学习(Graph Deep Learning)关注的趋势增大。它主要包括以下五大类模型：
半监督方法：包括图神经网络(GNN)和图卷积网络(GCN)
无监督方法：图自动编码器(GAE)
图递归神经网络（Graph RNN）和图强化学习(Graph RL)

图嵌入（graph embedding）、网络嵌入（network embedding）、网络表示学习（network representation learning），这三个概念从原理上来说其实表达的是同一件事，核心思想就是“通过深度学习技术将图中的节点（或边）映射为向量空间中的点，进而可以对向量空间中的点进行聚类、分类等处理”。而接下来讲的图卷积神经网络就属于图嵌入技术的一种。

一、GNN概述

GNN 论文：https://github.com/thunlp/GNNPapers
GNN是Graph Neural Network的简称，是用于学习包含大量连接的图的联结主义模型。当信息在图的节点之间传播时GNN会捕捉到图的独立性。与标准神经网络不同的是，GNN会保持一种状态，这个状态可以代表来源于人为指定的深度上的信息。

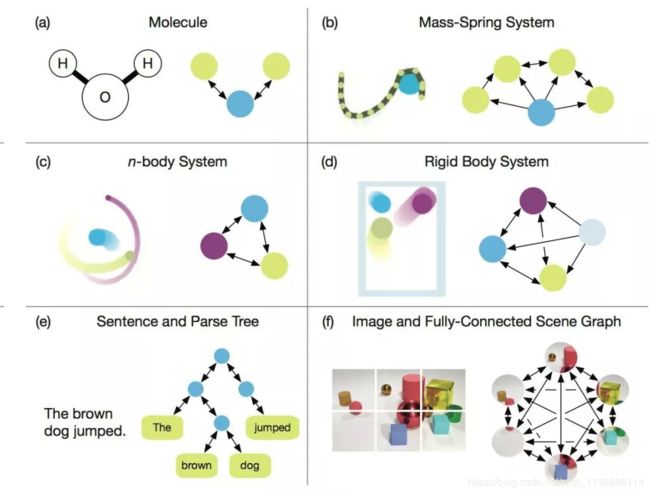
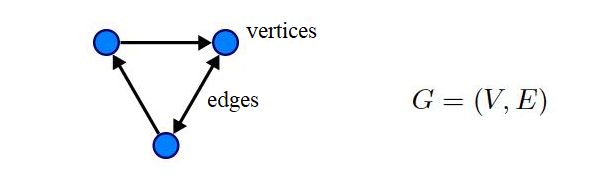
图神经网络处理的数据就是图(Graph)，而图是一种对节点和节点间关系建模的数据结构，是机器学习中唯一的非欧几里得数据，由顶点 (vertices) 和 边 (edges) 两个部件组成的一种数据结构，图分析可用于节点分类、链接预测和聚类。一个图 G 可以用它包含的 顶点 V 和边 E（有向或无向） 的集合来描述。

GNN的目标是学习到每个节点的邻居的状态嵌入，这个状态嵌入是向量且可以用来产生输出。GNN就是一种在图域上操作的深度学习方法。

图神经网络（Graph NNs）可能解决图灵奖得主Judea Pearl指出的深度学习无法做因果推理的核心问题。

1.1 GNN特点

基于CNN与graph embedding两种思想

• CNN特征提取：CNN可以提取大量本地紧密特征并组合为高阶特征，但CNN只能够操作欧几里得数据。CNN的关键在于局部连接、权值共享、多层使用；
• graph embedding降维操作：在低维向量上学习表示图节点、边或者子图。思想源于特征学习和单词嵌入，第一个图嵌入学习方法是DeepWalk，它把节点看做单词并在图上随机游走，并且在它们上面使用SkipGram模型；

GNN会在图结构上聚合信息，因此可以对输入/输出的元素及元素间的独立性进行建模。GNN还可以同时使用RNN核对图上的扩散过程进行建模。GNN也需要防止过拟合和欠拟合，由于图数据通常过大，所以可以采用随机游走的方式，来获取图的特征。

GNN的优势

标准神经网络（CNN、RNN）无法解决图输入无序性，因为它们将点的特征看做是特定的输入；

两点之间的边代表着独立信息，在标准神经网络中，这种信息被看做是点的信息，而GNN可以通过图结构来进行传播，而不是将其看做是特征；通常而言，GNN更新隐藏节点的状态，是通过近邻节点的权值和；

高级人工只能需要更高的可解释性；标准神经网络可以生成合成图像或文档，但无法生成图；GNN可以生成无结构的数据（多种应用：文字分类、神经机器翻译、关系提取、图像分类）；

GNN不足

更新节点的隐藏状态是低效的；

在迭代中使用相同的参数，更新节点隐藏状态是时序的；

在边上有一些信息化的特征无法在原始GNN中建模；如何学习边的隐藏状态也是问题；

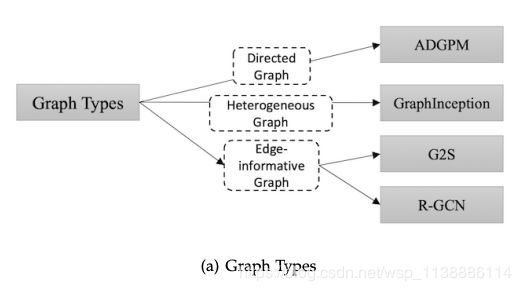
1.2 图类型与传播

原始GNN的输入图是带有标记信息的节点和无向边：

1. 有向图(Directed Graphs )：信息更紧密；
   图形的第一个变体是有向图。无向边可以看作是两个有向边，表明两个节点之间存在着关系。然而，有向边比无向边能带来更多的信息。例如，在一个知识图中，边从head实体开始到tail实体结束，head实体是tail实体的父类，这表明我们应该区别对待父类和子类的信息传播过程。有向图的实例有ADGPM (M. Kampffmeyer et. al. 2018)。
2. 异质图（Heterogeneous Graphs）：包含几种不同的节点，最简单的处理方式是one-hot feature vector；
3. 带边信息的图(Edge-informative Graph)：每个边也有信息、权值和类型，我们可以将边也变成节点，或者当传播时在不同的边上使用不同的权重矩阵；例如G2S和R-GCN。

1.3 训练方法与GNN变体

原始的图神经网络在训练和优化步骤有缺陷，它需要完整的图拉普拉斯，对大图而言计算力消耗大。更多的，层L上的节点嵌入是递归计算的，通过嵌入它的所有L-1层的邻居。因此，单层节点是成倍增长的，因此对节点的计算消耗巨大。且GCN是对每个固定图进行独立训练的，因此泛化能力不好。
使用不同训练方法的图变体

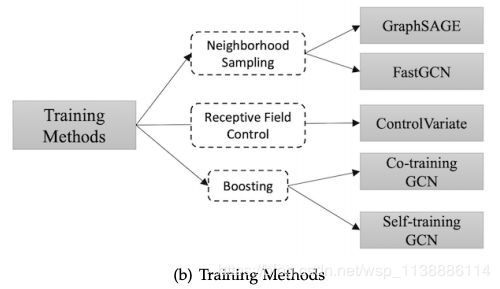
以下是几种改善方式：

1. GraphSAGE：将全图拉普拉斯替换为可学习聚合函数，是使用信息传递并生长到未见节点的关键，GraphSAGE还使用了邻居采样来避免接收域爆炸；
2. FastGCN：对采样算法做了更深的改进，FastGCN为每层直接采样接受域，而非对每个节点进行邻居采样；
3. control-variate based stochastic approximation：使用节点的历史激励作为控制随机数，此方法限制接受域为1跳邻居，但使用历史隐藏状态作为可接受最优化方法；
4. Co-Training GCN and Self-Training GCN：
   用于解决GCN需要许多额外的有标记数据及卷积过滤器的局部特征的限制，因此使用了此方法来扩大训练数据集，Co-Training方法为训练数据找到最近的邻居，Self-Training则采用了类似boosting的方法。

1.4 传播步骤与GNN变体

• 对GNN而言，传播步骤是非常重要的，它可以获得节点（边）的隐藏状态。传播步骤使用的方法通常是不同的聚合函数（在每个节点的邻居收集信息）和特定的更新函数（更新节点隐藏状态）。

• 在传播步骤进行修改的GNN变体
  

卷积操作

• 光谱方法：光谱方法在图的光谱表示上运行，学习的过滤器是基于拉普拉斯特征权重的，因此与图的结构紧密相关，难以泛化；
• 非光谱方法：直接在图上定义卷积，对紧密相近的节点进行操作，主要的挑战就是非光谱方法在不同大小的邻居上的定义和保持CNN的局部变量，非光谱方法具有点分类和图分类两种；

Gate闸门机制

• 在GNN中使用门限机制是为了减少限制并改善长期的图结构上的信息传递。

Attention注意力机制

• 注意力机制已经成功的应用于基于时序的任务，例如机器翻译、机器阅读等。GAT在传播步骤使用了注意力机制，会通过节点的邻居来计算节点的隐藏状态，通过自注意策略。

Skip connection

• 许多机器学习的应用都会使用多层神经网络，然而多层神经网络不一定更好，因为误差会逐层累积，最直接定位问题的方法，残差网络，是来自于计算机视觉。即使使用了残差网络，多层GCN依旧无法像2层GCN一样表现良好。
• 有一种方法是使用高速路GCN（Highway GCN），它像高速路网络一样使用逐层门限。

二、GNN框架

框架的目的是集合不同的模型。
有论文提出message passing neural network（MPNN），可以同一化多种图神经网络和图卷积网络方法。
non-local neural network（NLNN）则同一化了几个自注意方法。
graph network（GN）统一了MPNN和NLNN
还有其他的Interaction Networks，Neural Phsics Engine，CommNet， structure2vec，GGNN，Relation Network，Deep Sets和Point Net。

2.1 GNN的三大通用框架

MPNN
J. Gilmer等人(J. Gilmer et. al. 2017)提出了消息传递神经网络(message passing neural network， MPNN)，统一了各种图神经网络和图卷积网络方法。

MPNN是监督学习的框架，它抽象了几个最流行的用于处理图结构数据的模型的相似性。模型包括两个阶段，信息传递阶段和读出阶段。

• 信息传递阶段：
  就是传播阶段，会运行T次。是以信息传递函数和端点更新函数为定义的。
• 读出阶段：
  读出阶段会使用读出函数来对整个图计算特征向量。

NLNN
X. Wang等人(X. Wang et. al. 2017)提出了非局部神经网络(non-local neural network, NLNN)，它结合了几种“self-attention”风格的方法。

NLNN是用来对深度神经网络的长范围的独立性。non-local操作来源于经典non-local mean操作在计算机视觉上的应用。non-local操作会在一个位置上计算响应，同时加权了的特征和在所有点上。这些位置可以是空间、时间或者空间时间。因此NLNN可以看做是不同的自注意方法的统一。

一般的，non-local操作被如下定义：
$${\mathbf{h}}_i^{\prime }=\frac{1}{\mathcal{C}(\mathbf{h})}\sum _{{\forall }_j}f({\mathbf{h}}_i,{\mathbf{h}}_j)g({\mathbf{h}}_j)$$

其中，i是输出位置的索引，j是指出所有可能位置的索引，f函数计算i和j之间的缩放值，这可以代表他们之间的联系，g函数代表了输入的变换以及公式的系数用于正则化结果。当使用不同的f和g函数时，将得到不同的non-local操作实例，最简单的g函数就是线性变换了。以下是一些可能选择的f函数：

• Gaussian;
• Embedded Gaussian;
• Dot product;
• Concatenation;

P. W. Battaglia等人(P. W. Battaglia et. al. 2018)提出了图网络(graph network, GN)，它统一了统一了MPNN和NLNN方法以及许多其他变体，如交互网络(Interaction Networks)，神经物理引擎(Neural Physics Engine)，CommNet，structure2vec，GGNN，关系网络(Relation Network)，Deep Sets和Point Net。

GN
首先是图的定义然后是GN块，核心GN计算单元，计算步骤，最后是GN的基本设计原则。

• Graph definition：
  图被定义为三元组，（全局属性，节点集合，边集合）；
• GN block：
  GN块包括三个更新函数和三个聚合函数；
• Computation steps；
• Design Principles：

GN的设计基于三个基本原则：

flexible representation
configurable within-block structure
composable multi-block architectures

三、GNN的应用场景

GNN的应用场景非常多，因为GNN是应用于图信息的，而多种多样的数据都可以划分为图数据。以下是GNN的应用场景：
社交网络；
知识图谱；
推荐系统；
文字分类；
神经网络翻译；
关系提取；
图分类；
…
GNN 在对图形中节点间的依赖关系进行建模方面能力强大，使得图分析相关的研究领域取得了突破性进展。
在这里我们对GNN的应用进行简单的介绍，首先我们将其划分为三种场景的应用：

• 结构化场景：数据有明显的联系结构；
• 非结构化场景：联系结构不明显，例如图像、文字等；
  GNN在非结构场景中的应用，但我们没有找到从原始数据中生成图的最佳方法。在图像域中，一些研究可以利用CNN获取特征图，然后对其进行上采样，形成超像素作为节点，还有的直接利用一些对象检测算法来获取对象节点。在文本域中，有些研究使用句法树作为句法图，还有的研究采用全连接图。因此，关键是找到图生成的最佳方法，使GNN在更广泛的领域发挥更大的作用。
• 其他的应用场景：生成模型、组合最优化问题等；

启发

• GNN是对图数据进行处理的深度学习神经网络，它可以实现对异构数据的学习与表示，这里的图数据与我们通常所说的图是不一样的，这里的图指的是数据结构中的那种图以及离散数学中图论，其中不同的节点表示不同的信息。因此，图即代表实体及实体之间的联系。

在我们的日常生活中，图是无处不在的。而图结构数据具有一定的复杂性，因为图结构的数据节点通常具有是具有不同的类型的，因此对普通的神经网络而言处理起来具有一定的难度。

鸣谢：
如何理解 Graph Convolutional Network（GCN）：https://www.zhihu.com/question/54504471/answer/332657604
https://blog.csdn.net/qq_34911465/article/details/88524599