GCN的应用(交通预测)相关论文整理
文章目录
- T-GCN
- 早期研究
- 本文贡献
- ST-GCN
- 本文亮点
- 网络结构
- 时间模块
- 输出层
- ASTGCN
- 本文亮点
- 网络结构
- 时空注意力
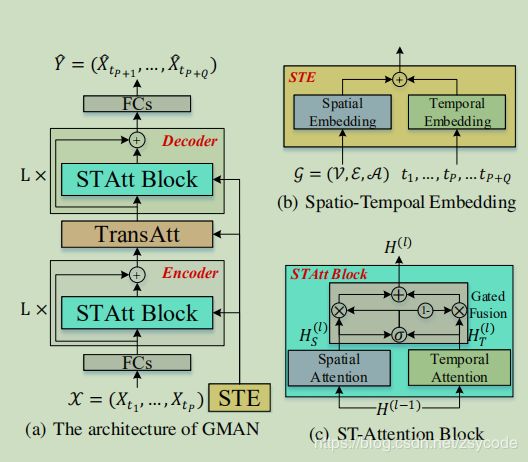
- GMAN
- 本文亮点
- 网络结构
- 时空嵌入（STE）
- 时空注意力模块
- 空间注意力
- 时间注意力
- 门控融合
- Transform Attention
- MRA-GGCN
- 本文贡献
- 网络细节
- Bicomponent Graph Convolution（双组件图卷积）
- Multi-Range Attention
- Bicomponent Graph Convolutional RNN
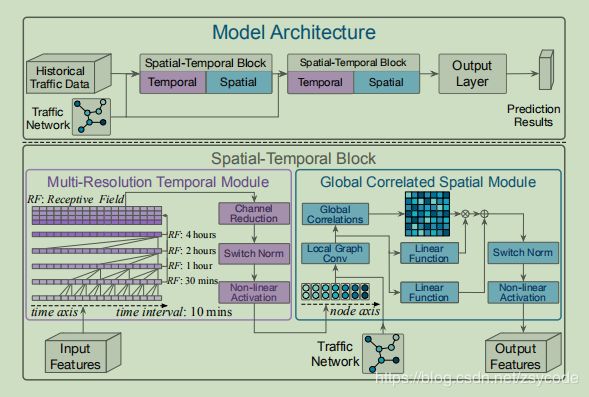
- GSTNet
- 问题提出
- 多分辨率时间模块
- 全局关联空间模块
- 输出层
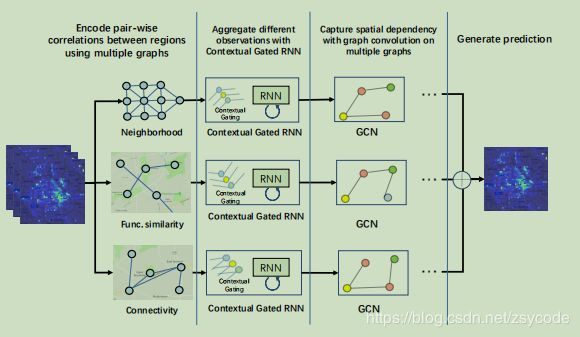
- ST-MGCN（预测打车需求量）
- 问题提出
- 网络结构
- 空间依赖建模
- 时间相关建模
- STG2Seq
- 问题描述
- 邻接矩阵的构建
- 长短期编码
T-GCN
早期研究
早期的方法只考虑了交通状况在时间上的动态变换，忽略可空间之间的相互依赖。一些研究引入了卷积神经网络来对空间特征进行提取，但普通卷积局限于处理像图像这种欧几里德结构的数据，对于交通数据这种复杂的拓扑结构效果不是很好。
本文贡献
本文引入了最近比较火的gcn，结合GRU来分别提取交通数据的空间特征和时间特征，达到不错的效果。网络也比较简单，亮点主要就是GCN的使用。
ST-GCN
本文亮点
- 第一次用纯卷积的形式来提取时间特征
- 提出了一个新的由时空块组成的神经网络，由于由于这个架构中是纯卷积操作，它比基于RNN的模型的训练速度快10倍以上，而且需要的参数更少。
注意： 在PeMSD7数据中，图的构建方法并不是基于实际路网，而是通过数学方法构建了一个基于距离关系的网络
网络结构
如上图，左边为整个网络，中间为ST-Conv Block具体结构，分为时间模块-空间模块-时间模块，来充分提取时空特征，空间模块就是gcn的应用。右边为时间模块的具体结构。
时间模块
尽管基于RNN的模型可以广泛的应用于时间序列分析，用于交通预测的循环神经网络仍然会遇到费时的迭代，复杂的门控机制，对动态变化的响应慢。相反，CNN训练快，结构简单，而且不依赖于前一步。
每个顶点的时间卷积的输入可以被看做是一个长度为M的序列，先进行一维卷积，即使用 1 ∗ K t 1*K_t 1∗Kt或 K t ∗ 1 K_t*1 Kt∗1大小的卷积核，这里使用 2 C o 2C_o 2Co个卷积核，得到的输出为 [ P Q ] ∈ R ( M − K t + 1 ) × ( 2 C o ) [P Q] \in \mathbb{R}^{(M-K_t+1) \times (2C_o)} [PQ]∈R(M−Kt+1)×(2Co)然后接了一个门控线性单元(GLU)作为激活，GLU定义为 Γ ∗ τ Y = P ⊗ σ ( Q ) ∈ R ( M − K t + 1 ) × C o \Gamma \ast_ \tau Y = P \otimes \sigma (Q) \in \mathbb{R}^{(M-K_t+1) \times C_o} Γ∗τY=P⊗σ(Q)∈R(M−Kt+1)×Co
⊗表示哈达玛积，文中还实现了残差连接，即P改为（P+X），X为时间模块的输入（为了实现残差，X直接取了 ( M − K t + 1 ) (M-K_t+1) (M−Kt+1)这个长度，即 X [ K t − 1 : ] X[K_t-1:] X[Kt−1:]）。
输出层
一个额外的时间卷积和全连接层。
ASTGCN
本文亮点
- 考虑了不同周期时间段的影响，即周、日、时，比如一周的周一，一天的早晨，这都是车流量较大的时候，网络分为三个组件分别提取邻近、日、周的依赖特征。
- 同样用gcn提取空间特征，普通卷积提取时间特征，但在此基础上加入了注意力机制。
网络结构
三个组件分别提取出日、天、周的时空特征，然后进行融合后得到最终输出
时空注意力
-
空间注意力
在空间维度上，不同位置的交通状况相互影响，相互影响具有很强的动态性。因此我们使用注意力机制自适应地捕捉空间维度中节点之间的动态关联性。
N为观测点的个数。 -
时间注意力
在时间维度上，不同时间段的交通状况之间存在相关性
T为时间步数。
GMAN
本文亮点
本文针对长时间交通预测，提出了一个图多注意力的网络。
作者认为，长时间交通预测的困难有两点：
1、复杂的时空关联性
2、对误差传递的敏感。每个时间步的误差在长时间的预测中都会被放大。
争对上述问题，本文贡献如下：
1、对空间和时间的相关性都采用了注意力的方式建模
2、提出一个变换注意力机制将历史交通特征转换为未来的表示。这个注意力机制对历史和未来的关系直接建模，减轻错误传播的问题。
3、该网络在一小时预测上性能提升不少。
网络结构
时空嵌入（STE）
由于交通条件的演变由底层道路网络限制，将道路网络信息纳入预测模型是至关重要的。作者使用node2vec学习节点表示，得到节点向量，再将其送入一个两层的全连接网络，得到空间嵌入 e v e_v ev。
空间嵌入是静态的，不能表示路网的动态关联性。使用one-hot编码加两层全连接层得到时间嵌入 e t e_t et。对于某一节点 v i v_i vi在时间 t i t_i ti的时空嵌入为 e v i , t i = e v i + e t i e_{v_i,t_i}=e_{v_i}+e_{t_i} evi,ti=evi+eti。
时空注意力模块
空间注意力
类似于图注意力网络（GAT）的思想，同样采用了多抽头注意力，求相关系数加入了时空嵌入。
h v i , t j h_{v_i,t_j} hvi,tj表示节点vi在时间点tj的隐藏状态， e v i , t j e_{v_i,t_j} evi,tj表示节点vi在时间点tj的时空嵌入。 V \mathcal{V} V表示所有节点。
当结点数 N 很大的时候，时间和内存消耗都会很大，达到 N 2 N^2 N2 的数量级。为了解决这个限制，我们提出了组空间注意力，包含了组内注意力分数和组间注意力分数。组内注意力计算同上，每组节点通过组内注意力更新后经最大池化得到各自表示，根据每组的表示计算组间注意力得到每组的全局特征，每组的节点加上各自的全局特征得到输出特征。
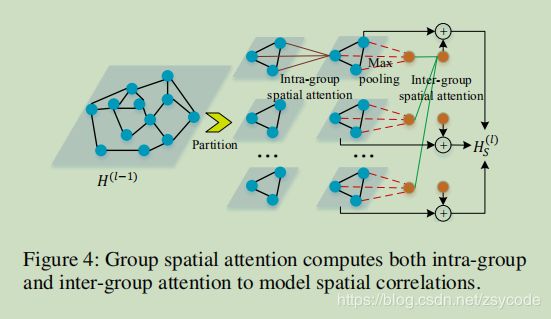
组空间注意力中，我们分为G组，每组 M = N / G M=N/G M=N/G个节点，每个时间步需要计算 G M 2 + G 2 = N M + ( N / M ) 2 GM^2+G^2=NM+(N/M)2 GM2+G2=NM+(N/M)2 个注意力分数。通过使 M M M的梯度为0，我们知道 M = 2 N 3 M = \sqrt[3]{2N} M=32N时计算步数达到最小 2 − 1 / 3 N 4 / 3 ≪ N 2 2^{-1/3} N^{4/3} \ll N^2 2−1/3N4/3≪N2.
时间注意力
时间注意力和空间注意力类似，只是改变下参照对象
N t j \mathcal{N}_{t_j} Ntj表示 t j t_j tj前的时间步。
更新公式同样类似
门控融合
Transform Attention
为了减轻错误传播的问题，我们在编码器和解码器之间加入了一个变换注意力层。它能直接地对历史时间步和未来时间步的关系建模，将交通特征编码为未来的表示，作为解码器的输入。
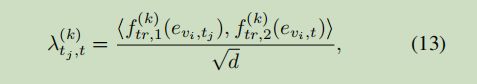
t t t表示历史时间步（ t = t 1 . . . t P t=t_1...t_P t=t1...tP）, t j t_j tj表示预测时间步（ t j = t P + 1 . . . t P + Q t_j=t_{P+1}...t_{P+Q} tj=tP+1...tP+Q）,只通过时空嵌入（ e e e）来衡量的。
MRA-GGCN
本文贡献
- 考虑了边的关系，通过对边构建图来提取边的相关性
- 提出了一个多级注意力机制，它能聚合不同邻域范围的信息，并学习到它们的重要性。
网络细节
Bicomponent Graph Convolution（双组件图卷积）
图卷积一般是对图中节点的关系建模，但在交通预测中，边的相互关系也是非常重要的。对于边图的构建分以下两种：
- Stream connectivity（流连接）
在交通网络中，一个路段是受它的上游和下游影响的。如图3（a），直观上，如果节点 j j j有大量的邻接节点（也就是 j j j的度越大）， ( i − > j ) (i->j) (i−>j)和 ( j − > k ) (j->k) (j−>k)这两边的的联系就越弱。计算其邻接矩阵 A e A_e Ae的权重公式如下
d e g − deg^- deg−表示入度， d e g + deg^+ deg+表示出度， σ \sigma σ表示节点度的标准差。 - Competitive relationship（竞争关系）
如图3（b）， ( i − > k ) (i->k) (i−>k)和 ( j − > k ) (j->k) (j−>k)由于共享目标节点 k 而产生竞争关系，类比于流连接，这两边的关联是受起始点的出度的影响。其权重计算公式如下：
对于 k 跳双组件图卷积就是堆叠 k 个这样的图卷积，公式定义如下：
M ∈ R ∣ V ∣ ∗ ∣ E ∣ M\in R^{|V|*|E|} M∈R∣V∣∗∣E∣，|V| 和 |E| 分别表示节点和边的个数，这个矩阵用来编码节点和边的联系，定义为 M i , i − > j = M j , i − > j = 1 M_{i,i->j}=M_{j,i->j}=1 Mi,i−>j=Mj,i−>j=1，其他情况值为 0 。 M Z ( . ) MZ^{(.)} MZ(.)对每个节点聚合边的信息， M T X ( . ) M^TX^{(.)} MTX(.)对每个边聚合节点信息。 W b W_b Wb是一个可学习的映射矩阵，用来将原始节点输入 X ( 0 ) X^{(0)} X(0)转化为原始边的输入 Z ( 0 ) Z^{(0)} Z(0)。
Multi-Range Attention
经过双组件图卷积模块得到 K 个不同邻域范围的节点表示
其相关系数的计算公式如下
（这个地方我觉得论文写错了，应该 X 和 W 调换位置）
是个可学习得向量。
再使用如下公式对每个节点进行更新
Bicomponent Graph Convolutional RNN
将GRU中的全连接层换成 MRA-BGCN形成BGCGRU，
表示为MRA-BGCN，X 为输入， Θ \Theta Θ为所有可训练参数。更新公式如下
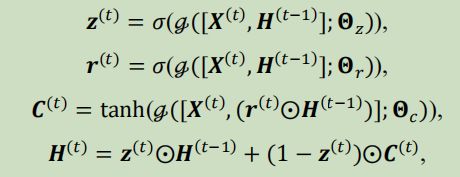
GSTNet
问题提出
从上图可以看出，E点与C、D邻近，但E点的流量分布与A、B相似。然而许多现有的研究只考虑了局部空间依赖，并没有考虑非局部（全局）的空间依赖（感觉jk-net正好也适用该问题），无法准确地预测像E点这样的流量信息。据此，作者提出了一个全新的网络结构，包含一个能同时提取长期依赖和短期依赖的时间模块，和一个能同时提取局部关联和全局关联的空间模块。
多分辨率时间模块
该模块实际就是由多层扩张卷积（在时间维度上扩张）组成的，增强了模型提取长期依赖的能力。
上述公式文章中称为张量因果卷积，实际从公式可以看出就是只在时间维度上扩张的卷积，d为扩张率。 K τ K_\tau Kτ为卷积核的长度。
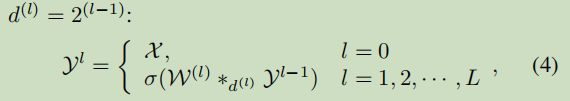
扩张率按指数级增长堆叠多层卷积层。不同层捕获不同分辨率的时间依赖，然后将各层输出拼接（感觉思想还是和jk-net类似）
h h h是个通道减少的卷积操作。
全局关联空间模块
用图卷积提取局部关联，设计如下公式提取全局关联（思想类似注意力机制，对一个点和其他所有点计算机相关度，然后更新节点）
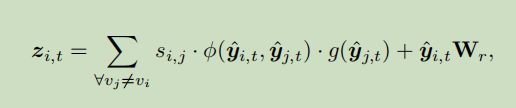
i是节点，t是时间，如果i、j有边 s i , j = β > = 1 s_{i,j}=\beta>=1 si,j=β>=1，否则 s i , j = 1 s_{i,j}=1 si,j=1。 ϕ \phi ϕ就是一个类似计算相关度的操作，
or
g g g是一个线性变换。后面的加法是一个残差连接的操作。
输出层
输出层在时间维度上使用了一个注意力机制，自适应地选择历史最相关的数据
ψ \psi ψ是计算内积，最后得出的输出即为预测结果。
注：该文章预测的是某个时间点的流量，并不是一个时间段的流量，所以最后输出维度不包含时间T，即
N为节点数，M为特征数。
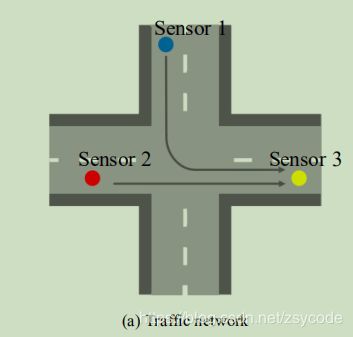
ST-MGCN（预测打车需求量）
问题提出
根据历史观察数据预测某个区域的打车需求量（和预测交通流量差不多）
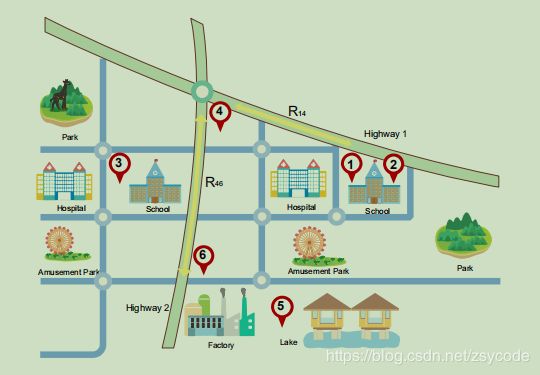
文中首先讨论了各个区域的空间相关性，如上图分为三类（以预测区域1为例）：
1、邻接区域2是很重要的
2、功能相似的区域3（都左右靠着医院和学校）同样存在相关性
3、交通链接的区域4也对预测存在影响
根据上述三个相关性，作者提出了一个多图卷积网络，也就是根据这三类分别定义了三种不同的邻接矩阵分别提取其空间相关性，最后将其聚合。
对于时间相关性作者借助了视觉中SE模块的思想和rnn来实现建模
网络结构
空间依赖建模
根据三种不同的空间相关性，定义了三种不同的图，节点不变，邻接矩阵不同
1、 邻居
对于一个区域在3*3的网格中选取8个邻接节点构建该图
2、功能相似
使用区域周围的POIs（Point of Interests）来衡量相似性
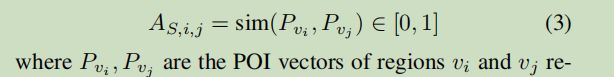
P v i ( v j ) P_{vi(vj)} Pvi(vj)表示区域 v i ( v j ) vi(vj) vi(vj)的POI向量（没看代码，不知道具体怎么计算的）
3、交通连接
conn是计算两节点连接度的函数，减去邻居连接是为了避免多余的连接
时间相关建模
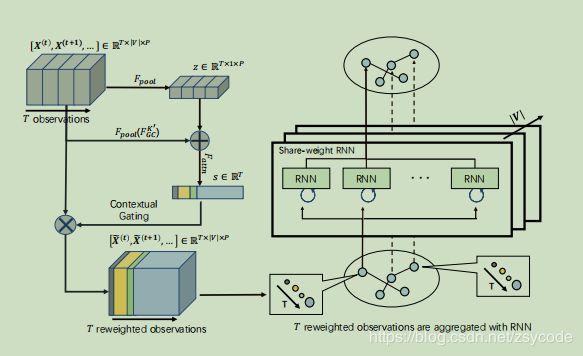
上图即为contextual gated rnn（CGRNN）。
t时间的数据 X ( t ) ∈ R ∣ V ∣ ∗ P X^{(t)}\in R^{|V|*P} X(t)∈R∣V∣∗P，
是个图卷积操作
接下来的三个公司就类似se模块啦，只是只争对节点数求平均了。
（公式感觉核图片上有点出入，待看了代码再细究）
接下来就输入一个共享的rnn
STG2Seq
同样，该论文也是解决乘客需求预测的问题，提出的模型分为三个部分：
1、一个长期编码器编码历史乘客需求
2、一个短期编码器导出下一步预测
3、一个基于注意力的输出模块来动态建模时间和通道信息
问题描述
用历史的乘客需求 D t ∈ R N ∗ d i n D_t \in R^{N*d_{in}} Dt∈RN∗din和时间特征 E t ∈ R d e E_t \in R^{de} Et∈Rde(包括该时间步所在的时程，星期几，和节假日)来学习一个映射函数，用来预测未来多个时间步的需求量。
邻接矩阵的构建
作者认为距离较远的区域由于具有相似的属性而用拥有相同的乘客需求模式，据此定义了邻接矩阵
其相似度使用了皮尔逊相关系数计算
0–t 单指训练集上的数据。
长短期编码
长短期编码都是由GGCM组成，GGCM每次取k个时间（ k ∗ N ∗ C k*N*C k∗N∗C）步作为输入，将其转化为 N ∗ ( k ∗ C ) N*(k*C) N∗(k∗C)用GCN提取，依次移动时间步，得到h个输出将其在时间轴上拼接得到 h ∗ N ∗ C o u t h*N*C^{out} h∗N∗Cout，该模块能同时提取时间和空间相关性。（对于短期这块的输入有点疑惑，不知道是不是根据已预测出的结果进行输入预测下一步还是直接选个最短的时间步作为输入）
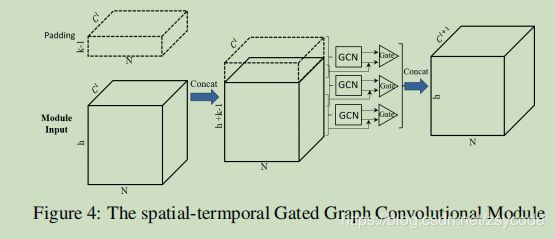
将长短期编码的输出在时间维度上进行拼接形成，然后分别经过一个时间和通道注意力得到最后输出（计算注意力分数中引用了时间特征 E T E_T ET）
