NOIP2017模拟赛(14) 总结

前言：本次测试是在家通过网络提交进行的，不出所料，我又考得十分“爆炸”，炸到我怀疑人生。

另外，由于以前有一些题目迟迟没有改完，所以我打算改完哪场比赛的题目就先写那场比赛的总结，避免遗忘和拖沓，虽然可能会有些乱。。。

---

a 最大得分

题目描述

“回文分数”游戏并不简单。游戏的目标是修改最多maxChanges个字符使得一个字符串word的回文分数最高。只允许修改，不许增加或者删除字符。
一个字符串的回文分数定义如下：

1、如果字符串不是回文串，则分数为0。
2、如果字符串是回文串，且长度为奇数，则分数为1。
3、如果字符串是回文串，且长度为偶数，我们将它分为左右两半。计算它的一半子串的回文分数为K（两个一半子串得分一定相同），则原字符串的回文分数为K + 1。

给定一个字符串word和一个型整数maxChanges，返回最多修改maxChanges个字符后最大可能的回文分数。

回文串的定义是一个字符串从前向后读和从后向前读完全一样。

---

输入格式

第一行:一个字符串 word
第二行:一个整数 maxChanges

word包含1到50个字符（含1和50）。
word 只包含小写字母 (‘a’-‘z’)。
maxChanges 取值范围是0到50（含0和50）。

---

输出格式

第一行: 一个整数 maximize

---

输入样例

输入样例一：

abcbxabcba
1

输入样例二：

coder
2

---

输出样例

输出样例一：

2

样例解释：
如果把x改成a，得到偶数长度的回文串”abcbaabcba”。它的一半子串是奇数长度的回文串”abcba”，所以子串分数为K = 1，因而最后得分是K + 1 = 2。

输出样例二：

1

样例解释：
我们可以把c改成r，把e改成o，得到”rodor”。这是一个奇数长度的回文串，所以得分为1。

---

解题思路(模拟+贪心)

这题做得我十分痛苦，其实这是一道比较简单的贪心+模拟题。我一开始的做法就是照着题目要求模拟，在一次比较，两个字符不同时，关键就是如何替换才使答案最优。如果随便替换的话将对后面的答案有影响。所以我当时的做法是处理一层的替换的时候看看下一层，怎样替换对下一层更优我就怎样替换。本质就是看看字符的出现个数。

然而这样未必对，我们知道，如果当前层对下一层一样优的话，对下下层可能不一样。但是我这样做也有94分，好一段时间内我不知道该怎么改。其实必须边递归边展开所有层判断是否能继续，再统计答案。由于层数不超过6层，所以这样不会超时。但这样的方法其实并不直观们还有一种更易理解的方法。

直接枚举答案,假如长度为12，枚举的答案为2，则可以表示为1 2 3 3 2 1 1 2 3 3 2 1，然后将相同数字的位置改成相同字符即可。如何改就贪心，改成哪个字符修改次数少就那么改，再和maxChanges比较判断答案。

---

Code

#include 
#include 
#include 
#include 
#include 
#include 
#define N 60

using namespace std;

char word[N];
int len, change, score, num[N];

int check(int a, int b, int l){
    memset(num, 0, sizeof(num));
    for(int i = 0; b+i*l < len; i++){
      num[word[a+i*l]-'a'] ++;
      if(a != b)  num[word[b+i*l]-'a'] ++;
    }
    int sum = 0, Max = 0;
    for(int i = 0; i < 26; i++)  sum += num[i], Max = max(Max, num[i]);
    return sum - Max;
}

int dfs(int l){
    if(l & 1){
      int res = 0;
      for(int i = 0; i <= l/2; i++)  res += check(i, l-i-1, l);
      if(res <= change)  return 1;
      return 0;
    }
    else{
      int res = 0;
      for(int i = 0; i < l/2; i++)  res += check(i, l-i-1, l);
      if(res <= change)  return dfs(l/2) + 1;
      return 0;
    }
}

int main(){

    scanf("%s", &word);
    scanf("%d", &change);

    len = strlen(word);

    score = dfs(len);
    printf("%d\n", score);

    return 0;
}

---

b 寄存器

题目描述

你有一台超小的电脑，内存只有两个寄存器：X和Y。寄存器只能存储正整数，一开始两个寄存器的值都是1，电脑操作系统只有两种指令：指令[X]和指令[Y]。
指令[X]的功能是：X ← X + Y，即把两寄存器目前的值累加到X寄存器；
指令[Y]的功能是：Y ← X + Y，即把两寄存器目前的值累加到Ｙ寄存器。例如：指令序列”XXYYX”的执行过程如下:

可以发现，执行指令序列”XXYYX”后，X寄存器的值是10，Y寄存器的值是7。现在你的任务是：给你一个正整数R, 你要编写指令序列，使得最后X寄存器的值是R (此时Y寄存器可以是任意整数). 当然，我们希望你编写的指令序列的长度要尽量短，在此前提下，如果有多种方案，请输出字典序最小的一种方案。

---

输入格式

多组测试数据。
第一行，一整正整数G,表示有G组测试数据，1 <= G <=5
每组测试数据格式：
　一个正整数R，其中 1 <= R <= 1000000。

---

输出格式

一个字符串，代表生成R的长度最短的指令序列。

---

输入样例

4
10
3
20
34

---

输出样例

XXYYX
XX
XYYYYXX
XYXYXYX

---

解题思路(更相减损术(迭代)+gcd)

如果直接宽搜，必定超时。
我们必须注意到一点，如果我们枚举一个Y，是可以直接根据最短步数得到方案的。
这个得到方案的方法就是在数学上有了解到的更相减损术。

容易证明，我们不断用大数减小数，得到的差和较小数再次重复做这个操作，不断迭代，步数一定是最短的。根据一些方法，我们可以知道可能的最少步数不会超过三十几步，这里我是用斐波那契数列去发现的(然后考试时我就想歪了。。)。

于是时间就是枚举Y(1e6)然后乘上个三十几。至于枚举的Y不一定是合法的，合法的前提是与给出的X互质，为什么呢？因为更相减损术就是在求gcd啊！于是不与X互质的Y必然不会产生合法答案。然后就写个欧几里德算法判断，时间照样不成问题。不过考试时我思维僵化，连方向都错了。

字典序就做完一次判断更新答案。如果算的过程中，答案长度已经超过可能的最优长度(三十几)或当前答案，就不用往下做了，直接跳过，这样可以节省很多时间。最后倒叙输出答案就行了。

坑点：第一是特判，然后不要用字符串，要用字符数组记录答案，否则超时。。

---

Code

#include 
#include 
#include 
#include 
#include 
#include 
#define oo 0x7fffffff
#define ban 32

using namespace std;

int G, R;
char ans[40], res[40];
int len;

int Gcd(int a, int b){
    if(!b)  return a;
    return Gcd(b, a % b);
}

void Work(int X, int Y){

    int l = 0;
    while(X != Y){
      if(X > Y){
        res[l++] = 'X';
        X = X - Y;
      }
      else{
        res[l++] = 'Y';
        Y = Y - X;
      }
      if(l > ban || l > len)  return;
    }

    if(l < len){
      len = l;
      for(int i = 0; i < len; i++)  ans[i] = res[i];
    }
    else if(l == len){
      bool f;
      for(int i = len-1; i >= 0; i--)
        if(ans[i] != res[i]){
          if(ans[i] > res[i])  f = true;
          else  f = false;
          break;
        }
      if(f)  for(int i = 0; i < len; i++)  ans[i] = res[i];
    }
}

int main(){
    scanf("%d", &G);
    while(G --){

      scanf("%d", &R);
      len = oo;
      for(int i = 1; i < R; i++){
        if(Gcd(R, i) != 1)  continue;
        Work(R, i);
      }

      if(R == 1)  len = 0;
      for(int i = len-1; i >= 0; i--)  putchar(ans[i]);
      printf("\n");
    }
    return 0;
}

---

c 肯德基

题目描述

FJ最近得到了一份工作，那就是送肯德基外卖。FJ所在的小镇可以看作是R行C列矩形，被划分成R×C个单元格子，从上往下，行的编号是1至R；从左往右，列的编号是1至C。FJ一开始在第1行第1列的格子处，他收到D个顾客的订单，第i个顾客的位置在第Ri行第Ci列的格子。FJ一开始就把所有顾客的订餐一起装在背包里，这样在送餐过程中就没必要一定要返回出发点了，FJ必须严格按照次序给顾客送肯德基（即先送完第1个顾客，再送第2个顾客，…依次类推）。当送完所有的肯德基外卖后，FJ也没有必要返回出发处。FJ每一步的移动规则是这样的：FJ可以从当前格子移动一步，到达相邻的左格子或者相邻的右格子（两个格子相邻是指它们有公共边）；此外，如果FJ当前所在格的列是第1列或者第C列，那么FJ还可以向上移动一格或者向下移动一格。任意时刻，FJ都不能走出矩形的边界。FJ每进入一个格子，都会在该格子停留一定的时间T，在不同的给子，FJ停留的时间可能不同。FJ送完所有订餐，至少需要多少时间？

---

输入格式

第一行，两个整数，R和C。
接下来有R行C列，第i行第j列的整数表示FJ进入第i行第j列的格子，必须在那个格子停留的时间T
接下来一行，有一个整数D，表示有D个顾客订餐。
接下来有D行，每行两个整数，依次表示顾客的位置，即所在行和所在列。 顾客所在的位置没有重复。

【数据范围】
对于70%的数据，1 <= R <= 250, 1 <= C <= 200。
对于100%的数据，1 <= R <= 2000, 1 <= C <= 200,
1 <= D <= 200000， 0 <=T<=5000。

---

输出格式

一个整数，送完所有订餐的最少时间。

---

输入样例

输入样例一：

3 3
1 8 2
2 3 2
1 0 1
3
1 3
3 3
2 2

输入样例二：

2 5
0 0 0 0 0
1 4 2 3 2
4
1 5
2 2
2 5
2 1

---

输出样例

输出样例一：

17

输出样例二：
9

样例一解释：
FJ可以按如下的格子顺序走：
(1, 1)–>(2, 1)–> (3, 1)–>(3, 2)–> (3, 3)–> (2, 3)–> (1, 3)–> (2, 3)–>(3, 3)–> (2, 3)–>(2, 2)。其中三个顾客的位置依次用红四表示，总时间是：1+2+1+0+1+2+2+2+1+2+3=17.

---

解题思路(SPFA/DP+分类讨论)

首先要吐槽一下题目的翻译，FJ送肯德基。。
令人fz的翻译。。

本题多种做法，我在考试时没时间了(吃晚饭)，于是写了一个狂暴的SPFA，地图上每个点都提出来做最短路，拿了50分。然而最短裤(路)能拿70分，dp是满分。

首先讲讲SPFA的方法求最短路。
我们发现由于只有第一列和最后一列是可以向下向上走的，其他的只能横着走，于是我们将那两列点单独拿出来做一遍SPFA，建图、做法就不用说了，维护行和列的前缀和，这样就得到了这两列点互相到达的最短路了。注意这里做2n次SPFA，时间复杂度的级别是 O(2∗n∗k∗m) ，k是SPFA的常数，m是边数，与点数成正比，这样其实理论是n^2的，但是常数太大，所以很慢。但实测也是能过的（前提是加了玄学优化）。

算出那些点的最短路后，对于每组询问，我们分5种情况，设二点为A和B，第一列为1，最后一列为m，则

1.A->A1->B1->B
2.A->A1->B2->B
3.A->A2->B1->B
4.A->A2->B2->B
5.A->B(A和B在同一行)

上面所有行的第三个箭头都是沿最短路走，其他的打横走就查询部分和。于是，通过SPFA求最短路，分类讨论取最小值，就可以解决此题了。不过SPFA部分我写的比较复杂，也不如下面的DP方法巧妙。

其实DP的做法也是在求最短路。
不过，计算最短路的时间是严格的 O(4n2) 。首先我们除了 dis[i][j] 表示点 i 与 j 的最短路外，我们要先预处理出一个 cost 数组。 cost[i] 表示第i行的左边的点向右边的点走的最短路径。就是从第一列的某个点出发，通过各种“蛇皮走位”，到达同行的最后一列的最短路径。

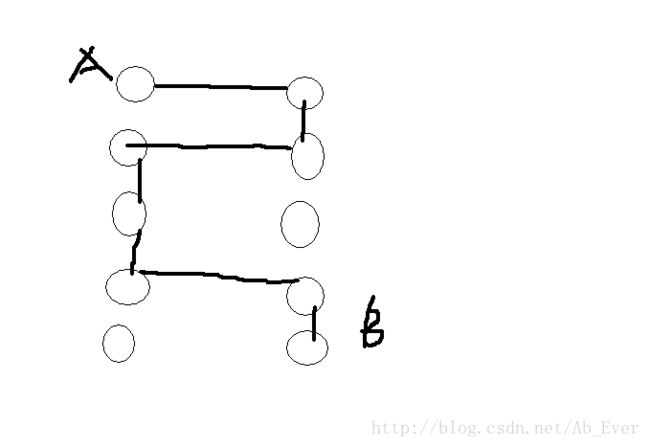
为什么要先算这个呢？假设不是同一行的点，最短路径可能绕很多次。如下图

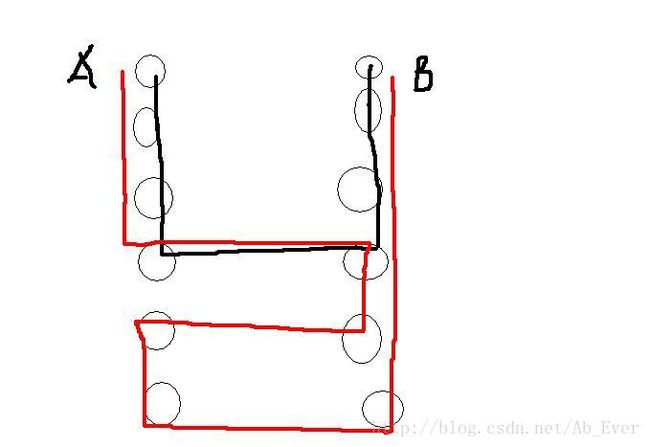
当行数变多，拐的弯可能越来越多，枚举拐点是不太可行的。而当同一行时，拐一次一定是最优的。如图

若红色的是最短路，由于T非负，毫无疑问黑色的路径更优。

那我们枚举拐点求出 cost[] ，然后用 cost 去更新 dis 数组。具体的更新就是按照如下次序：

如果当前最短路的源点在左边，更新次序就是第i行的右边，再到第i行的左边，反之就相反。更新的方法就是用部分和与 cost ，具体的公式参见代码，注意不要算重算漏。

预处理的时候我们知道每个点到自己的最短路和对面的最短路。然后n^2按行数向下更新就行了，只向下是为了避免重复计算。

最后一样的分类讨论算出答案。

---

Code(SPFA)

#include 
#include 
#include 
#include 
#include 
#include 
#define N 2010
#define INF 0x7fffffff

using namespace std;

typedef long long LL;
int n, m, D;
LL Ans;

int dis[N<<1][N<<1], sum[N][N], stop[N][N];
int q[N<<1];
bool vis[N<<1];


int GX(int now){
    return (now <= n) ? now : now - n;
}

int GY(int now){
    return (now <= n) ? 1 : m;
}

int GOP(int now){
    return (now <= n) ? now + n : now - n;
}

void SPFA(int S){
    for(int i = 1; i <= (n<<1); i++)  dis[S][i] = INF;
    memset(vis, false, sizeof(vis));
    vis[S] = true;
    dis[S][S] = stop[GX(S)][GY(S)];
    int head, tail, Mod = (n<<1) + 2;
    q[head = tail = 0] = S;
    while(head <= tail){
      int now = q[head%Mod];
      head ++;
      if(GX(now) > 1){
        if(dis[S][now] + stop[GX(now-1)][GY(now)] < dis[S][now-1]){
          dis[S][now-1] = dis[S][now] + stop[GX(now-1)][GY(now)];
          if(!vis[now-1]){
            vis[now-1] = true;
            tail ++;
            q[tail%Mod] = now-1;
            if(dis[S][q[head%Mod]] > dis[S][q[tail%Mod]])  swap(q[head%Mod], q[tail%Mod]);
          }
        }
      }
      if(GX(now) < n){
        if(dis[S][now] + stop[GX(now+1)][GY(now)] < dis[S][now+1]){
          dis[S][now+1] = dis[S][now] + stop[GX(now+1)][GY(now)];
          if(!vis[now+1]){
            vis[now+1] = true;
            tail ++;
            q[tail%Mod] = now+1;
            if(dis[S][q[head%Mod]] > dis[S][q[tail%Mod]])  swap(q[head%Mod], q[tail%Mod]);
          }
        }
      }

      if(dis[S][now] + sum[GX(now)][m] - stop[GX(now)][GY(now)] < dis[S][GOP(now)]){
        dis[S][GOP(now)] = dis[S][now] + sum[GX(now)][m] - stop[GX(now)][GY(now)];
        if(!vis[GOP(now)]){
          vis[GOP(now)] = true;
          tail ++;
          q[tail%Mod] = GOP(now);
          if(dis[S][q[head%Mod]] > dis[S][q[tail%Mod]])  swap(q[head%Mod], q[tail%Mod]);
        }
      }
      vis[now] = false;
    }
}

int main(){

    scanf("%d%d", &n, &m);

    for(int i = 1; i <= n; i++)
     for(int j = 1; j <= m; j++)  
       scanf("%d", &stop[i][j]);

    for(int i = 1; i <= n; i++){
      sum[i][0] = 0;
      for(int j = 1; j <= m; j++)  sum[i][j] = sum[i][j-1] + stop[i][j];
    }

    for(int i = 1; i <= (n<<1); i++)  SPFA(i);

    scanf("%d", &D);

    Ans = (LL)stop[1][1];
    int ox = 1, oy = 1, nx, ny, temp1, temp2, temp3, temp4;
    for(int i = 1; i <= D; i++){

      scanf("%d%d", &nx, &ny);

      temp1 = sum[ox][oy-1] - stop[ox][1] + dis[ox][nx] + sum[nx][ny] - stop[nx][1];
      temp2 = sum[ox][oy-1] - stop[ox][1] + dis[ox][nx+n] + sum[nx][m] - sum[nx][ny-1] - stop[nx][m];
      temp3 = sum[ox][m] - sum[ox][oy] - stop[ox][m] + dis[ox+n][nx] + sum[nx][ny] - stop[nx][1];
      temp4 = sum[ox][m] - sum[ox][oy] - stop[ox][m] + dis[ox+n][nx+n] + sum[nx][m] - sum[nx][ny-1] - stop[nx][m];
      LL res = (LL)min(min(temp1, temp2), min(temp3, temp4));
      if(ox == nx)  res = min(res, (LL)(sum[ox][max(ny, oy)] - sum[ox][min(ny, oy)-1] - stop[ox][oy]));
      Ans += res;
      ox = nx;
      oy = ny;
    }

    printf("%lld\n", Ans);

    return 0;
}

---

Code(DP)

#include 
#include 
#include 
#include 
#include 
#include 
#define N 2017
#define INF 0x7fffffff

using namespace std;

typedef long long LL;

int n, m, D;
int stop[N][N], cost[N];
int sumN[N][N], sumM[N][N];
int dis[N<<1][N<<1];
LL Ans;

int main(){

    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i++)
     for(int j = 1; j <= m; j++)
       scanf("%d", &stop[i][j]);

    for(int i = 1; i <= n; i++){
      sumN[i][0] = 0;
      for(int j = 1; j <= m; j++)  sumN[i][j] = sumN[i][j-1] + stop[i][j];
    }

    for(int j = 1; j <= m; j++){
      sumM[0][j] = 0;
      for(int i = 1; i <= n; i++)  sumM[i][j] = sumM[i-1][j] + stop[i][j];
    }

    for(int i = 1; i <= n; i++){
      cost[i] = INF;
      for(int j = 1; j <= n; j++)
        cost[i] = min(cost[i], sumN[j][m-1] - sumN[j][1] + sumM[max(i, j)][1] - sumM[min(i, j)-1][1] + sumM[max(i, j)][m] - sumM[min(i, j)-1][m]);
    }


    for(int i = 1; i <= (n<<1); i++)
     for(int j = 1; j <= (n<<1); j++)
       dis[i][j] = INF;

    for(int i = 1; i <= n; i++){
      dis[i][i] = stop[i][1];
      dis[i+n][i+n] = stop[i][m];
      dis[i][i+n] = dis[i+n][i] = cost[i];
    }

    for(int i = 1; i < n; i++){
      for(int j = i+1; j <= n; j++){
        dis[i][j+n] = dis[j+n][i] = min(dis[i][j-1+n]+stop[j][m], dis[i][j-1]+cost[j]);
        dis[i][j] = dis[j][i] = min(dis[i][j-1]+stop[j][1], dis[i][j+n]+cost[j]-stop[j][m]);
      }
    }

    for(int i = 1; i < n; i++){
      for(int j = i+1; j <= n; j++){
        dis[i+n][j] = dis[j][i+n] = min(dis[i+n][j-1]+stop[j][1], dis[i+n][j-1+n]+cost[j]);
        dis[i+n][j+n] = dis[j+n][i+n] = min(dis[i+n][j-1+n]+stop[j][m], dis[i+n][j]+cost[j]-stop[j][1]);
      }
    }

    scanf("%d", &D);

    Ans = (LL)stop[1][1];
    int ox = 1, oy = 1, nx, ny, temp1, temp2, temp3, temp4;
    for(int i = 1; i <= D; i++){
      scanf("%d%d", &nx, &ny);
      temp1 = sumN[ox][oy-1] - stop[ox][1] + dis[ox][nx] + sumN[nx][ny] - stop[nx][1];
      temp2 = sumN[ox][oy-1] - stop[ox][1] + dis[ox][nx+n] + sumN[nx][m] - sumN[nx][ny-1] - stop[nx][m];
      temp3 = sumN[ox][m] - sumN[ox][oy] - stop[ox][m] + dis[ox+n][nx] + sumN[nx][ny] - stop[nx][1];
      temp4 = sumN[ox][m] - sumN[ox][oy] - stop[ox][m] + dis[ox+n][nx+n] + sumN[nx][m] - sumN[nx][ny-1] - stop[nx][m];
      LL res = (LL)min(min(temp1, temp2), min(temp3, temp4));
      if(ox == nx)  res = min(res, (LL)(sumN[ox][max(ny, oy)] - sumN[ox][min(ny, oy)-1] - stop[ox][oy]));
      Ans += res;
      ox = nx;
      oy = ny;
    }

    printf("%lld\n", Ans);

    return 0;
}

---

总结

考试时很不在状态，简单的题居然脑抽不会做，还有希望以后改题写总结能快点，不然很多事情都做不了，好好把握时间才行，争取多做有意义的事，提高水平。

---

愿你走出半生 归来仍是少年