AeroYoung
AeroYoung

C# 逆波兰表达式解析公式

你是否遇到这样的需求：如何计算“1.0+3/2-tan(45)/(1+1)+Abs(-10)-floor(2.55)” 这一串字符串的值？

 

思路：

定义：

逆波兰表达式又叫做后缀表达式。在通常的表达式中，二元运算符总是置于与之相关的两个运算对象之间，这种表示法也称为中缀表示。波兰逻辑学家J.Lukasiewicz于1929年提出了另一种表示表达式的方法，按此方法，每一运算符都置于其运算对象之后，故称为后缀表示。

人类最熟悉的一种表达式1+2，(1+2)*3，3+42+4等都是中缀表示法。对于人们来说，也是最直观的一种求值方式，先算括号里的，然后算乘除，最后算加减，但是，计算机处理中缀表达式却并不方便。

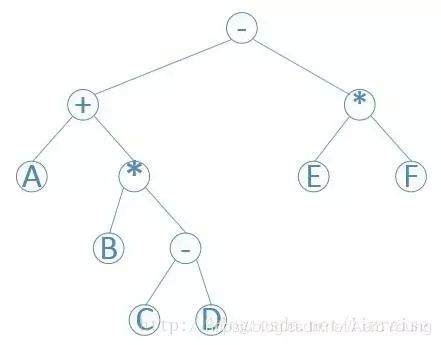
然后我们还需明确一些概念，下面通过我们最熟悉的中缀表达式画出一棵语法树来直观认识一下前后缀表达式的生成。以A+B*(C-D)-E*F为例：

C# 逆波兰表达式解析公式_第1张图片

从上面可以发现，其实问题就2个：

1. 将人类常用的中缀表达式转换为后缀表达式

2. 计算后缀表达式。

转换为后缀表达式

这里我们要用到堆栈Stack, 详细概念可以点这里。

1.数字直接入栈
2.运算符要与栈顶元素比较
 ①栈为空直接入栈
 ②运算符优先级大于栈顶元素优先级则直接入栈
 ③小于或等于则出栈入列，再与栈顶元素进行比较，直到运算符优先级小于栈顶元
    素优先级后，操作符再入栈
3.操作符是 ( 则无条件入栈
4.操作符为 )，则依次出栈入列，直到匹配到第一个(为止，此操作符直接舍弃，(直接出栈舍弃

代码实现如下，首先定义操作数类型，因为我们不仅想计算简单的加减乘除，还想实现一些简单的函数和逻辑运算。

    /// 
    /// 操作数类型
    /// 
    public enum Type
    {
        /// 
        /// 函数
        /// 
        FUNC = 1,

        /// 
        /// 日期
        /// 
        DATE = 2,

        /// 
        /// 数字
        /// 
        NUMBER = 3,

        /// 
        /// 布尔
        /// TODO 
        /// 
        BOOLEAN = 4,

        /// 
        /// 字符串
        /// 
        STRING = 5
    }

然后我们定义一个操作数类：

    /// 
    /// 操作数类
    /// 
    public class Operand
    {
        public Operand(Type type, object value)
        {
            this.Type = type;
            this.Value = value;
        }

        public Operand(string opd, object value)
        {
            this.Type = ConvertOperand(opd);
            this.Value = value;
        }
       
        /// 
        /// 操作数类型
        /// 
        public Type Type { get; set; }

        /// 
        /// 关键字
        /// 
        public string Key { get; set; }

        /// 
        /// 操作数值
        /// 
        public object Value { get; set; }

        /// 
        /// 转换操作数到指定的类型
        /// 
        /// 操作数
        /// 返回对应的操作数类型
        public static Type ConvertOperand(string opd)
        {
            if (opd.IndexOf("(") > -1)
            {
                return Type.FUNC;
            }
            else if (IsNumber(opd))
            {
                return Type.NUMBER;
            }
            else if (IsDate(opd))
            {
                return Type.DATE;
            }
            else
            {
                return Type.STRING;
            }
        }

        /// 
        /// 判断对象是否为数字
        /// 
        /// 对象值
        /// 是返回真,否返回假
        public static bool IsNumber(object value)
        {
            return Regex.IsMatch(value.ToString(), @"^[+-]?\d*[.]?\d*$");
            // return double.TryParse(value.ToString(), out _); 用正则表达式快一点
        }

        /// 
        /// 判断对象是否为日期
        /// 
        /// 对象值
        /// 是返回真,否返回假
        public static bool IsDate(object value)
        {
            return DateTime.TryParse(value.ToString(), out _);
        }
    }

然后定义运算符的枚举，从小到大优先级递减：

    /// 
    /// 运算符类型(从上到下优先级依次递减)，数值越大，优先级越低
    /// 
    public enum OptType
    {
        #region 最高优先级操作符

        /// 
        /// 左括号:(,left bracket
        /// 
        LB = 1,

        /// 
        /// 右括号),right bracket
        /// 
        RB = 2,

        /// 
        /// 逻辑非,!,NOT
        /// 
        NOT = 3,

        /// 
        /// 正号,+,positive sign
        /// 
        PS = 5,

        /// 
        /// 负号,-,negative sign
        /// 
        NS = 7,

        #endregion

        #region 函数

        /// 
        /// 正切，tan
        /// 
        TAN = 10,

        /// 
        /// 正切，tan
        /// 
        COT = 11,

        /// 
        /// 反正切，atan
        /// 
        ATAN = 12,

        /// 
        /// 正弦
        /// 
        SIN = 13,

        /// 
        /// 余弦
        /// 
        COS = 14,

        /// 
        /// 绝对值
        /// 
        Abs = 15,
        
        /// 
        /// 开平方
        /// 
        Sqrt = 16,

        /// 
        /// 向下取整
        /// 
        Floor = 17,

        /// 
        /// 向上取整
        /// 
        Ceiling = 18,

        /// 
        /// 四舍五入2位小数
        /// 
        Round = 19,

        /// 
        /// 平方
        /// 
        Pow = 20,

        /// 
        /// 立方
        /// 
        Cube = 21,

        /// 
        /// 自然对数
        /// 
        Ln = 22,

        /// 
        /// 10为底的对数
        /// 
        Log = 23,

        #endregion

        #region 其他操作符

        /// 
        /// 乘,*,multiplication
        /// 
        MUL = 130,

        /// 
        /// 除,/,division
        /// 
        DIV = 131,

        /// 
        /// 余,%,modulus
        /// 
        MOD = 132,

        /// 
        /// 加,+,Addition
        /// 
        ADD = 140,

        /// 
        /// 减,-,subtraction
        /// 
        SUB = 141,

        /// 
        /// 小于,less than
        /// 
        LT = 150,

        /// 
        /// 小于或等于,less than or equal to
        /// 
        LE = 151,

        /// 
        /// 大于,>,greater than
        /// 
        GT = 152,

        /// 
        /// 大于或等于,>=,greater than or equal to
        /// 
        GE = 153,

        /// 
        /// 等于,=,equal to
        /// 
        ET = 160,

        /// 
        /// 不等于,unequal to
        /// 
        UT = 161,

        /// 
        /// 逻辑与,&,AND
        /// 
        AND = 170,

        /// 
        /// 逻辑或,|,OR
        /// 
        OR = 171,

        /// 
        /// 逗号,comma
        /// 
        CA = 180,

        /// 
        /// 结束符号 @
        /// 
        END = 255,

        /// 
        /// 错误符号
        /// 
        ERR = 256

        #endregion
        
    }

再定义一个运算符类，用来把输入字符串中的运算符提取出来：

    /// 
    /// 运算符类
    /// 
    public class Operator
    {
        public Operator(OptType type, string value)
        {
            this.Type = type;
            this.Value = value;
        }

        /// 
        /// 运算符类型
        /// 
        public OptType Type { get; set; }

        /// 
        /// 运算符值
        /// 
        public string Value { get; set; }

        /// 
        /// 对于>或者<运算符，判断实际是否为>=,<>、<=，并调整当前运算符位置
        /// 
        /// 当前运算符
        /// 当前表达式
        /// 当前运算符位置
        /// 返回调整后的运算符
        public static string AdjustOperator(string currentOpt, string currentExp, ref int currentOptPos)
        {
            #region 操作符 <>

            if (currentOpt == "<")
            {
                if (currentExp.Substring(currentOptPos, 2) == "<=")
                {
                    currentOptPos++;
                    return "<=";
                }

                if (currentExp.Substring(currentOptPos, 2) != "<>") return "<";
                currentOptPos++;
                return "<>";
            }
            else if (currentOpt == ">")
            {
                if (currentExp.Substring(currentOptPos, 2) == ">=")
                {
                    currentOptPos++;
                    return ">=";
                }

                return ">";
            }

            #endregion
            
            var firstChar = false; // currentOpt是否和函数的首字母匹配
            var funcs = new List
            {
                "tan","cot", "atan", "sin", "cos",
                "abs", "sqrt",
                "floor", "ceiling",
                "round","pow","cube","ln","log"
            };

            foreach (var func in funcs)
            {
                var first = func.Substring(0, 1);
                if (currentExp.StartsWith(first, StringComparison.CurrentCultureIgnoreCase))
                    firstChar = true;

                if (!currentExp.StartsWith(func, StringComparison.CurrentCultureIgnoreCase)) 
                    continue;

                currentOptPos += func.Length - 1;
                return func;
            }

            return firstChar ? "error" : currentOpt;
        }
        
        /// 
        /// 转换运算符到指定的类型
        /// 
        /// 运算符
        /// 返回指定的运算符类型
        public static OptType ConvertOperator(string opt)
        {
            opt = opt.ToLower(); // svn add 307

            switch (opt)
            {
                case "~": return OptType.NS;
                case "!": return OptType.NOT;
                case "+": return OptType.ADD;
                case "-": return OptType.SUB;
                case "*": return OptType.MUL;
                case "/": return OptType.DIV;
                case "%": return OptType.MOD;
                case "<": return OptType.LT;
                case ">": return OptType.GT;
                case "<=": return OptType.LE;
                case ">=": return OptType.GE;
                case "<>": return OptType.UT;
                case "=": return OptType.ET;
                case "&": return OptType.AND;
                case "|": return OptType.OR;
                case ",": return OptType.CA;
                case "@": return OptType.END;
                case "tan": return OptType.TAN;
                case "cot": return OptType.COT;
                case "atan": return OptType.ATAN;
                case "sin": return OptType.SIN; // svn add 307
                case "cos": return OptType.COS; 
                case "abs": return OptType.Abs;
                case "sqrt": return OptType.Sqrt;
                case "floor": return OptType.Floor;
                case "ceiling": return OptType.Ceiling;
                case "round": return OptType.Round;
                case "pow": return OptType.Pow;
                case "cube": return OptType.Cube;
                case "ln": return OptType.Ln;
                case "log": return OptType.Log;

                default: return OptType.ERR;
            }
        }
        
        /// 
        /// 运算符优先级比较
        /// 
        /// 运算符类型A
        /// 运算符类型B
        /// A与B相比，-1，低；0,相等；1，高
        public static int ComparePriority(OptType optA, OptType optB)
        {
            if (optA == optB)
            {
                //A、B优先级相等
                return 0;
            }

            //乘,除,余(*,/,%)
            if ((optA >= OptType.MUL && optA <= OptType.MOD) &&
                (optB >= OptType.MUL && optB <= OptType.MOD))
            {
                return 0;
            }
            //加,减(+,-)
            if ((optA >= OptType.ADD && optA <= OptType.SUB) &&
                (optB >= OptType.ADD && optB <= OptType.SUB))
            {
                return 0;
            }
            //小于,小于或等于,大于,大于或等于(<,<=,>,>=)
            if ((optA >= OptType.LT && optA <= OptType.GE) &&
                (optB >= OptType.LT && optB <= OptType.GE))
            {
                return 0;
            }
            //等于,不等于(=,<>)
            if ((optA >= OptType.ET && optA <= OptType.UT) &&
                (optB >= OptType.ET && optB <= OptType.UT))
            {
                return 0;
            }
            //函数  
            if (optA >= OptType.TAN && optA < OptType.MUL && optB >= OptType.TAN && optB < OptType.MUL)
            {
                return 0;
            }

            if (optA < optB)
            {
                //A优先级高于B
                return 1;
            }

            //A优先级低于B
            return -1;
        }
    }

接下来就是重点：如何将字符串转换为后缀表达式：

首先定义一个解析类，然后添加一个堆栈和一个运算符字符串list（后续所有代码都在在此类之下）：

public class RPN
{
        /// 
        /// 最终逆波兰式堆栈
        /// 
        public Stack Tokens { get; } = new Stack();

        /// 
        /// 允许使用的运算符
        /// 
        public readonly List m_Operators = new List(new[]
        {
            "(", "tan", ")", "atan", "cot", "sin", "cos", "abs", "sqrt", "floor", "ceiling",
            "round", "pow","cube","ln","log",
            "~", "!", "*", "/", "%", "+", "-", "<", ">", "=", "&", "|", ",", "@"
        });
} 
  
添加2个容错函数，用来检查括号是否匹配，查找操作符等：
 
  
        /// 
        /// 检查表达式中特殊符号(双引号、单引号、井号、左右括号)是否匹配      
        /// 
        /// 
        /// 
        private static bool IsMatching(string exp)
        {
            string opt = "";    //临时存储 " ' # (

            for (int i = 0; i < exp.Length; i++)
            {
                string chr = exp.Substring(i, 1);   //读取每个字符
                if ("\"'#".Contains(chr))   //当前字符是双引号、单引号、井号的一种
                {
                    if (opt.Contains(chr))  //之前已经读到过该字符
                    {
                        opt = opt.Remove(opt.IndexOf(chr), 1);  //移除之前读到的该字符，即匹配的字符
                    }
                    else
                    {
                        opt += chr;     //第一次读到该字符时，存储
                    }
                }
                else if ("()".Contains(chr))    //左右括号
                {
                    if (chr == "(")
                    {
                        opt += chr;
                    }
                    else if (chr == ")")
                    {
                        if (opt.Contains("("))
                        {
                            opt = opt.Remove(opt.IndexOf("("), 1);
                        }
                        else
                        {
                            return false;
                        }
                    }
                }
            }
            return (opt == "");
        }

        /// 
        /// 从表达式中查找运算符位置
        /// 
        /// 表达式
        /// 要查找的运算符
        /// 返回运算符位置
        private int FindOperator(string exp, string findOpt)
        {
            var opt = "";
            for (var i = 0; i < exp.Length; i++)
            {
                var chr = exp.Substring(i, 1);
                if ("\"'#".Contains(chr))//忽略双引号、单引号、井号中的运算符
                {
                    if (opt.Contains(chr))
                    {
                        opt = opt.Remove(opt.IndexOf(chr), 1);
                    }
                    else
                    {
                        opt += chr;
                    }
                }

                if (opt != "") 
                    continue;

                if (findOpt != "")
                {
                    if (findOpt == chr)
                    {
                        return i;
                    }
                }
                else
                {
                    //modify svn 307 忽略大小写
                    if (m_Operators.Exists(x => x.IndexOf(chr, StringComparison.CurrentCultureIgnoreCase) > -1))
                        return i;
                }
            }
            return -1;
        }

 
  
接下来解析字符串，转换为后缀表达式。但是在正式转换前还需要做一些容错提高代码的健壮性：
 
  
其实也就是检查括号是否配对、中文符号转换为西文符号
 
  
        public bool Parse(string exp)
        {
            #region 容错

            Tokens.Clear();//清空语法单元堆栈
            if (exp.Trim() == "")//表达式不能为空
                return false;
            else if (!IsMatching(exp))//括号、引号、单引号等必须配对
                return false;

            exp = exp.Replace("（", "(");
            exp = exp.Replace("）", ")");
            exp = exp.Replace("！", "!");
            exp = exp.Replace("\\", "/");

            #endregion
        }
 
  
在容错后，再将圆周率Π用字符串替换的形式弄进去，因为担心未来有的函数名字中包含PI两个字符从而导致bug，所有我写代码要求PI必须全是大写，而其他函数不区分大小写（tan/Tan, Abs/abs）。
 
  
exp = exp.Replace("PI", $"({Math.PI})");
 
  
接下来要考虑的问题是：减号“-”和负号“-”是相同的，但是减号是二元运算符、正负号是一元运算符。如果程序中将两者等量齐观，则后面转换后缀表达式和计算都带来不必要的麻烦。所以之前定义运算符的时候，就把加减、正负这两组运算做了区分。此处我们要添加一个函数，就是把正负号+-替换为特殊符号和普通的加减号作为区分：
 
  
        /// 
        /// 将正负号替换为 # @
        /// 
        /// 
        /// 
        public string ReplaceNegative(string exp)
        {
            var len = exp.Length;
            var expT = exp.ToArray();
            var symbols = new[] {'+', '-', '*', '/', '^', '(', ',', '<', '>', '=' };

            for (var i = len - 1; i > -1; i--)
            {
                if (expT[i] == '-' && i > 1)
                    if (symbols.Contains(exp[i - 1]))
                        expT[i] = '~';

                if (expT[i] == '-' && i == 1) 
                    expT[i] = '~';


                if (expT[i] == '+' && i > 1)
                    if (symbols.Contains(exp[i - 1]))
                        expT[i] = '#';

                if (expT[i] == '+' && i == 1)
                    expT[i] = '#';
            }

            exp = string.Join("", expT).Replace("#", "");

            return exp;
        }
 
  
我这里偷个懒，直接把正号给省略掉了。
 
  
最后就是转换后缀表达式了:
 
  
            exp = ReplaceNegative(exp);

            #region 解析

            var nums = new Stack();         //操作数堆栈
            var operators = new Stack();      //运算符堆栈
            var optType = OptType.ERR;             //运算符类型
            var curNum = "";                            //当前操作数
            var curOpt = "";                            //当前运算符
            var curPos = 0;                             //当前位置
            var funcCount = 0;                          //函数数量

            curPos = FindOperator(exp, "");

            exp += "@"; //结束操作符
            while (true)
            {
                curPos = FindOperator(exp, "");

                curNum = exp.Substring(0, curPos).Trim();
                curOpt = exp.Substring(curPos, 1);

                //存储当前操作数到操作数堆栈
                if (curNum != "")
                    nums.Push(new Operand(curNum, curNum));

                //若当前运算符为结束运算符，则停止循环
                if (curOpt == "@")
                    break;

                //若当前运算符为左括号,则直接存入堆栈。
                if (curOpt == "(")
                {
                    operators.Push(new Operator(OptType.LB, "("));
                    exp = exp.Substring(curPos + 1).Trim();
                    continue;
                }

                //若当前运算符为右括号,则依次弹出运算符堆栈中的运算符并存入到操作数堆栈,直到遇到左括号为止,此时抛弃该左括号.
                if (curOpt == ")")
                {
                    while (operators.Count > 0)
                    {
                        if (operators.Peek().Type != OptType.LB)
                        {
                            nums.Push(operators.Pop());
                        }
                        else
                        {
                            operators.Pop();
                            break;
                        }
                    }
                    exp = exp.Substring(curPos + 1).Trim();
                    continue;
                }

                //调整运算符 获得完整函数名
                curOpt = Operator.AdjustOperator(curOpt, exp, ref curPos);

                optType = Operator.ConvertOperator(curOpt);

                //若运算符堆栈为空,或者若运算符堆栈栈顶为左括号,则将当前运算符直接存入运算符堆栈.
                if (operators.Count == 0 || operators.Peek().Type == OptType.LB)
                {
                    operators.Push(new Operator(optType, curOpt));
                    exp = exp.Substring(curPos + 1).Trim();
                    continue;
                }

                //若当前运算符优先级大于运算符栈顶的运算符,则将当前运算符直接存入运算符堆栈顶部.
                if (Operator.ComparePriority(optType, operators.Peek().Type) > 0)
                {
                    operators.Push(new Operator(optType, curOpt));
                }
                else
                {
                    //若当前运算符若比运算符堆栈栈顶的运算符优先级低或相等，则输出栈顶运算符到操作数堆栈，
                    //直至运算符栈栈顶运算符低于（不包括等于）该运算符优先级，
                    //或运算符栈栈顶运算符为左括号
                    //并将当前运算符压入运算符堆栈。
                    while (operators.Count > 0)
                    {
                        if (Operator.ComparePriority(optType, operators.Peek().Type) <= 0 && 
                            operators.Peek().Type != OptType.LB)
                        {
                            nums.Push(operators.Pop());

                            if (operators.Count != 0) 
                                continue;

                            operators.Push(new Operator(optType, curOpt));
                            break;
                        }
                        else
                        {
                            operators.Push(new Operator(optType, curOpt));
                            break;
                        }
                    }

                }
                exp = exp.Substring(curPos + 1).Trim();
            }
            //转换完成,若运算符堆栈中尚有运算符时,
            //则依序取出运算符到操作数堆栈,直到运算符堆栈为空
            while (operators.Count > 0)
            {
                nums.Push(operators.Pop());
            }
            //调整操作数栈中对象的顺序并输出到最终栈
            while (nums.Count > 0)
            {
                Tokens.Push(nums.Pop());
            }

            return true;

            #endregion 
  
计算后缀表达式
 
  
基于前面定义的类和转换得到的堆栈，计算后缀表达式其实挺简单。下面代码中还有很多函数没有添加、或与非逻辑运算也没有写，看官可以自己试试加上去
 
  
        /// 
        /// 对逆波兰表达式求值
        /// 
        /// 
        public object Evaluate()
        {
            /*
              逆波兰表达式求值算法：
              1、循环扫描语法单元的项目。
              2、如果扫描的项目是操作数，则将其压入操作数堆栈，并扫描下一个项目。
              3、如果扫描的项目是一个二元运算符，则对栈的顶上两个操作数执行该运算。
              4、如果扫描的项目是一个一元运算符，则对栈的最顶上操作数执行该运算。
              5、将运算结果重新压入堆栈。
              6、重复步骤2-5，堆栈中即为结果值。
            */

            try
            {
                if (Tokens.Count == 0) return null;

                object value = null;
                var opds = new Stack();
                var pars = new Stack();
                Operand opdA;
                Operand opdB;
                foreach (var item in Tokens)
                {
                    if (item is Operand operand)
                    {
                        //如果为操作数则压入操作数堆栈
                        opds.Push(operand);
                    }
                    else
                    {
                        switch (((Operator)item).Type)
                        {
                            #region 其他

                            case OptType.LB:
                                continue;
                            case OptType.RB:
                                continue;
                            case OptType.PS:
                                continue;

                            #endregion

                            #region ~ Negtive 取负数

                            case OptType.NS:
                                opdA = opds.Pop();
                                if (Operand.IsNumber(opdA.Value))
                                {
                                    opds.Push(new Operand(Type.NUMBER,
                                        -1.0 * double.Parse(opdA.Value.ToString())));
                                }
                                else
                                {
                                    throw new Exception("Negative运算的操作数必须为数字");
                                }
                                break;

                            #endregion

                            #region 乘,*,multiplication
                            case OptType.MUL:
                                opdA = opds.Pop();
                                opdB = opds.Pop();
                                if (Operand.IsNumber(opdA.Value) && Operand.IsNumber(opdB.Value))
                                {
                                    opds.Push(new Operand(Type.NUMBER, double.Parse(opdB.Value.ToString()) * double.Parse(opdA.Value.ToString())));
                                }
                                else
                                {
                                    throw new Exception("乘运算的两个操作数必须均为数字");
                                }
                                break;
                            #endregion

                            #region 除,/,division
                            case OptType.DIV:
                                opdA = opds.Pop();
                                opdB = opds.Pop();
                                if (Operand.IsNumber(opdA.Value) && Operand.IsNumber(opdB.Value))
                                {
                                    opds.Push(new Operand(Type.NUMBER, double.Parse(opdB.Value.ToString()) / double.Parse(opdA.Value.ToString())));
                                }
                                else
                                {
                                    throw new Exception("除运算的两个操作数必须均为数字");
                                }
                                break;
                            #endregion

                            #region 余,%,modulus
                            case OptType.MOD:
                                opdA = opds.Pop();
                                opdB = opds.Pop();
                                if (Operand.IsNumber(opdA.Value) && Operand.IsNumber(opdB.Value))
                                {
                                    opds.Push(new Operand(Type.NUMBER, double.Parse(opdB.Value.ToString()) % double.Parse(opdA.Value.ToString())));
                                }
                                else
                                {
                                    throw new Exception("余运算的两个操作数必须均为数字");
                                }
                                break;
                            #endregion

                            #region 加,+,Addition

                            case OptType.ADD:
                                opdA = opds.Pop();
                                if (opds.Count > 0)
                                {
                                    opdB = opds.Pop();
                                    if (Operand.IsNumber(opdA.Value) && Operand.IsNumber(opdB.Value))
                                        opds.Push(new Operand(Type.NUMBER, double.Parse(opdB.Value.ToString()) + double.Parse(opdA.Value.ToString())));
                                    else
                                        throw new Exception("加运算的两个操作数必须均为数字");
                                    break;
                                }
                                throw new Exception("加运算的操作数必须均为数字");
                                
                            #endregion

                            #region 减,-,subtraction
                            case OptType.SUB:
                                opdA = opds.Pop();
                                if (opds.Count > 0)
                                {
                                    opdB = opds.Pop();
                                    if (Operand.IsNumber(opdA.Value) && Operand.IsNumber(opdB.Value))
                                        opds.Push(new Operand(Type.NUMBER,
                                            double.Parse(opdB.Value.ToString()) - double.Parse(opdA.Value.ToString())));
                                    else
                                        throw new Exception("减运算的两个操作数必须均为数字");
                                    break;
                                }
                                throw new Exception("减运算的操作数必须均为数字");

                            #endregion

                            #region 逻辑运算符 true 1 false -1

                            case OptType.NOT: // 非
                                opdA = opds.Pop();
                                if (Operand.IsNumber(opdA.Value))
                                    opds.Push(
                                        new Operand(Type.NUMBER,
                                            double.Parse($"{opdA.Value}") > 0 ? -1 : 1)
                                    );
                                else
                                    throw new Exception("加运算的两个操作数必须均为数字");
                                break;

                            case OptType.LT:
                                break;
                            case OptType.LE:
                                break;
                            case OptType.GT:
                                break;
                            case OptType.GE:
                                break;
                            case OptType.ET:
                                break;
                            case OptType.UT:
                                break;
                            case OptType.AND:
                                break;
                            case OptType.OR:
                                break;
                            case OptType.CA:
                                break;

                            #endregion

                            #region 正切,tan,subtraction

                            case OptType.TAN:
                                opdA = opds.Pop();
                                if (Operand.IsNumber(opdA.Value))
                                {
                                    opds.Push(new Operand(Type.NUMBER, Math.Tan(double.Parse(opdA.Value.ToString()) * Math.PI / 180)));
                                }
                                else
                                {
                                    throw new Exception("正切运算的1个操作数必须均为角度数字");
                                }
                                break;

                            #endregion

                            #region 余切,cot

                            case OptType.COT:
                                opdA = opds.Pop();
                                if (Operand.IsNumber(opdA.Value))
                                {
                                    opds.Push(new Operand(Type.NUMBER,
                                        1.0 / Math.Tan(double.Parse(opdA.Value.ToString()) * Math.PI / 180)));
                                }
                                else
                                {
                                    throw new Exception("余切运算的1个操作数必须均为角度数字");
                                }
                                break;

                            #endregion

                            #region 反正切,atan,subtraction
                            case OptType.ATAN:
                                opdA = opds.Pop();
                                if (Operand.IsNumber(opdA.Value))
                                {
                                    opds.Push(new Operand(Type.NUMBER, Math.Atan(double.Parse(opdA.Value.ToString()))));
                                }
                                else
                                {
                                    throw new Exception("反正切运算的1个操作数必须均为数字");
                                }
                                break;
                            #endregion

                            #region 正弦,sin 角度

                            case OptType.SIN:
                                opdA = opds.Pop();
                                if (Operand.IsNumber(opdA.Value))
                                {
                                    opds.Push(new Operand(Type.NUMBER,
                                        Math.Sin(double.Parse(opdA.Value.ToString()) * Math.PI / 180)));
                                }
                                else
                                {
                                    throw new Exception("正弦运算的1个操作数必须均为角度数字");
                                }
                                break;

                            #endregion

                            #region 余弦,cos 角度

                            case OptType.COS:
                                opdA = opds.Pop();
                                if (Operand.IsNumber(opdA.Value))
                                {
                                    opds.Push(new Operand(Type.NUMBER,
                                        Math.Cos(double.Parse(opdA.Value.ToString()) * Math.PI / 180)));
                                }
                                else
                                {
                                    throw new Exception("正弦运算的1个操作数必须均为角度数字");
                                }
                                break;

                            #endregion

                            #region Abs

                            case OptType.Abs:
                                opdA = opds.Pop();
                                if (Operand.IsNumber(opdA.Value))
                                {
                                    opds.Push(new Operand(Type.NUMBER,
                                        Math.Abs(double.Parse(opdA.Value.ToString()))));
                                }
                                else
                                {
                                    throw new Exception("abs运算的1个操作数必须为数字");
                                }
                                break;

                            #endregion

                            #region Floor

                            case OptType.Floor:
                                opdA = opds.Pop();
                                if (Operand.IsNumber(opdA.Value))
                                {
                                    opds.Push(new Operand(Type.NUMBER,
                                        Math.Floor(double.Parse(opdA.Value.ToString()))));
                                }
                                else
                                {
                                    throw new Exception("Floor运算的1个操作数必须为数字");
                                }
                                break;

                            #endregion

                            #region Ceiling

                            case OptType.Ceiling:
                                opdA = opds.Pop();
                                if (Operand.IsNumber(opdA.Value))
                                {
                                    opds.Push(new Operand(Type.NUMBER,
                                        Math.Ceiling(double.Parse(opdA.Value.ToString()))));
                                }
                                else
                                {
                                    throw new Exception("Ceiling运算的1个操作数必须为数字");
                                }
                                break;

                            #endregion

                            #region 开平方 Sqrt
                                
                            case OptType.Sqrt:
                                opdA = opds.Pop();
                                if (Operand.IsNumber(opdA.Value))
                                {
                                    opds.Push(new Operand(Type.NUMBER,
                                        Math.Sqrt(double.Parse(opdA.Value.ToString()))));
                                }
                                else
                                {
                                    throw new Exception("sqrt运算的1个操作数必须为非负数");
                                }
                                break;

                            #endregion

                            #region 四舍五入

                            case OptType.Round:
                                opdA = opds.Pop();
                                if (Operand.IsNumber(opdA.Value))
                                {
                                    opds.Push(new Operand(Type.NUMBER,
                                        Math.Round(double.Parse(opdA.Value.ToString()), 2)));
                                }
                                else
                                {
                                    throw new Exception("四舍五入运算的1个操作数必须是数字");
                                }
                                break;

                            #endregion

                            #region 幂

                            case OptType.Pow:
                                opdA = opds.Pop();
                                if (Operand.IsNumber(opdA.Value))
                                {
                                    opds.Push(new Operand(Type.NUMBER,
                                        Math.Pow(double.Parse(opdA.Value.ToString()), 2)));
                                }
                                else
                                {
                                    throw new Exception("幂运算的1个操作数必须是数字");
                                }
                                break;

                            case OptType.Cube:
                                opdA = opds.Pop();
                                if (Operand.IsNumber(opdA.Value))
                                {
                                    opds.Push(new Operand(Type.NUMBER,
                                        Math.Pow(double.Parse(opdA.Value.ToString()), 3)));
                                }
                                else
                                {
                                    throw new Exception("幂运算的1个操作数必须是数字");
                                }
                                break;

                            #endregion

                            #region 对数

                            case OptType.Ln:
                                opdA = opds.Pop();
                                if (Operand.IsNumber(opdA.Value))
                                {
                                    opds.Push(new Operand(Type.NUMBER,
                                        Math.Log(double.Parse(opdA.Value.ToString()))));
                                }
                                else
                                    throw new Exception("对数运算的1个操作数必须是数字");
                                break;

                            case OptType.Log:
                                opdA = opds.Pop();
                                if (Operand.IsNumber(opdA.Value))
                                {
                                    opds.Push(new Operand(Type.NUMBER,
                                        Math.Log10(double.Parse(opdA.Value.ToString()))));
                                }
                                else
                                    throw new Exception("对数运算的1个操作数必须是数字");
                                break;

                                #endregion

                            case OptType.END:
                                break;
                            case OptType.ERR:
                                break;
                            default:
                                throw new ArgumentOutOfRangeException();
                        }
                    }
                }

                if (opds.Count == 1)
                    value = opds.Pop().Value;

                return value;
            }
            catch
            {
                return null;
            }
            
        } 
  
 
 
  
 
 
  

                            
                        
                    
                    
                    

                    
                    
                    

                
                

                    
                

            
        
    
    

        
你可能感兴趣的:(C#)

        

            

                
    
                    
  • C#中使用split分割字符串
                        互联网打工人no1
c#
                        
    1、用字符串分隔：usingSystem.Text.RegularExpressions;stringstr="aaajsbbbjsccc";string[]sArray=Regex.Split(str,"js",RegexOptions.IgnoreCase);foreach(stringiinsArray)Response.Write(i.ToString()+"");输出结果：aaabbbc
    
                    
    • 
                    
  • 你可能遗漏的一些C#/.NET/.NET Core知识点
                        追逐时光者
C#.NETDotNetGuide编程指南c#.net.netcoremicrosoft
                        
    前言在这个快速发展的技术世界中，时常会有一些重要的知识点、信息或细节被忽略或遗漏。《C#/.NET/.NETCore拾遗补漏》专栏我们将探讨一些可能被忽略或遗漏的重要知识点、信息或细节，以帮助大家更全面地了解这些技术栈的特性和发展方向。拾遗补漏GitHub开源地址https://github.com/YSGStudyHards/DotNetGuide/blob/main/docs/DotNet/D
    
                    
    • 
                    
  • C#动态加载DLL程序集及使用反射创建实例-简记
                        不全
C#相关Asp.netWebFormAsp.netMVCc#Assembly反射程序集
                        
    Assembly动态加载程序集：分两种情况：1、需要加载的程序集已经在程序中被引用了，则直接从当前程序域中查找即可：Assemblyassembly=AppDomain.CurrentDomain.GetAssemblies().FirstOrDefault(x=>x.GetName().Name.Contains("theAssemblyName"));2、需要加载的程序集未被加载，则使用程序集
    
                    
    • 
                    
  • 开发游戏的学习规划
                        杰克逊的日记
游戏学习
                        
    第一阶段：●C#语言快速系统地学习一遍（基础的语法、面向对象、基础的数据结构、基础的设计模式）●Unity的2D和3D部分及UI、动画、物理系统●阶段性测验：需要去用前面所学的这些基础知识来完成一个简单的2d或者3d的案例，将通过一个自制的《Flappybird》游戏案例讲解游戏开发的思想及方法，并将《Flappybird》这个游戏进一步改造成一个横版射击类游戏《Crazybird》以巩固并且升华
    
                    
    • 
                    
  • python可以制作大型游戏_python能做游戏吗-python能开发游戏吗
                        靖dede
python可以制作大型游戏
                        
    python可以写游戏，但不适合。下面我们来分析一下具体原因。用锤子能造汽车吗？谁也没法说不能吧？历史上也确实曾经有些汽车，是用锤子造出来的。但一般来说，还是用工业机器人更合适对吗？比较大型的，使用Python的游戏有两个，一个是《EVE》，还有一个是《文明》。但这仅仅是个例，没有广泛意义。一般来说，用来做游戏的语言，有两种。一是C++。。一是C#。。Python理论上，不仅不适合做游戏，而是只要
    
                    
    • 
                    
  • 【C#生态园】深度剖析：C#嵌入式开发工具大揭秘
                        friklogff
C#生态园c#开发语言
                        
    C#嵌入式开发：全面了解六大框架与库前言随着物联网和嵌入式系统的快速发展，越来越多的开发者开始关注使用C#语言进行嵌入式开发。本文将介绍几种用于C#的嵌入式开发框架和相关库，以及它们的核心功能、安装配置方法和API概览，帮助读者了解并选择适合自己项目的工具和资源。欢迎订阅专栏：C#生态园文章目录C#嵌入式开发：全面了解六大框架与库前言1.nanoFramework：一个用于C#的嵌入式开发框架1.
    
                    
    • 
                    
  • Lua 与 C#交互
                        z2014z
luac#开发语言
                        
    Lua与C#交互前提Lua是一种嵌入式脚本语言，Lua的解释器是用C编写的，因此可以方便的与C/C++进行相互调用。轻量级Lua语言的官方版本只包括一个精简的核心和最基本的库，这使得Lua体积小、启动速度快，也适合嵌入在别的程序里。交互过程C#调用Lua:由C#文件调用Lua解析器底层dll库（由C语言编写），再由dll文件执行相应的Lua文件。Lua调用C#：1、Wrap方式：首先生成C#源文件
    
                    
    • 
                    
  • C# 开发教程-入门基础
                        天马3798
教程系列整理c#开发语言
                        
    1.C#简介、环境，程序结构2.C#基本语法，变量，控制局域，数据类型，类型转换3.C#数组、循环，Linq4.C#类，封装，方法5.C#枚举、字符串6.C#面相对象，继承，封装，多态7.C#特性、属性、反射、索引器8.C#委托，事件，集合，泛型9.C#匿名方法10.C#多线程更多：JQuery开发教程入门基础Vue开发基础入门教程Vue开发高级学习教程
    
                    
    • 
                    
  • C# 禁止程序重复启动
                        wiseyao1219
c#
                        
    修改：Program.cs[STAThread]staticvoidMain(){Mutexmutex=newMutex(true,"NewGuid123456",outboolisCreatedNew);if(!isCreatedNew){MessageBox.Show(Application.ProductName+"isrunning...");return;}Application.Ena
    
                    
    • 
                    
  • C#中判断socket是否已断开的方法
                        wiseyao1219
c#
                        
    代码如下：Sockets=newSocket(..);if(s.Poll(-1,SelectMode.SelectRead)){intnRead=s.Receive();if(nRead==0){//socket连接已断开}}参考：C#中判断socket是否已断开的方法
    
                    
    • 
                    
  • C#文件被占用的解决方案
                        花北城
C#项目文件占用
                        
    问题打更新包时，提示文件被占用。System.IO.IOException:文件“D:\RS\RS_CCVI20111210.exe”正由另一进程使用，因此该进程无法访问该文件。在System.IO.__Error.WinIOError(Int32errorCode,StringmaybeFullPath)在System.IO.FileStream.Init(Stringpath,FileMode
    
                    
    • 
                    
  • C#实现软件自动升级
                        BruceEditCode

                        
    winform程序相对web程序而言，功能更强大，编程更方便，但软件更新却相当麻烦，要到客户端一台一台地升级，本文结合实际情况，通过软件实现自动升级，弥补了这一缺陷，有较好的参考价值。由于程序在运行时不能用新的版本覆盖自己，因此，我们将登录窗口单独做成一个可执行文件，用户登录时，从网上检测是否有新的主程序，如果有，则从后台下载并覆盖老的版本，用户输入正确的用户名和密码后，通过参数将必要的信息（如用
    
                    
    • 
                    
  • C# 自动化
                        TineAine
C#代码片段自动化c#自动化模拟操作
                        
    实现的方法可能很笨，但是确实很好用usingSystem;usingSystem.Collections.Generic;usingSystem.Linq;usingSystem.Runtime.InteropServices;usingSystem.Text;usingSystem.Threading;usingSystem.Threading.Tasks;/******************
    
                    
    • 
                    
  • 技术周总结 09.09~09.15周日(C# WinForm WPF)
                        打破砂锅问到底007
wpfc#WinForm
                        
    文章目录一、09.09周一1.1)问题01:Windows桌面开发中，WPF和WinForm的区别和联系？联系：区别：二、09.12周四2.1）问题01：visualstudio的相关快捷键有哪些？通用快捷键编辑导航调试窗口管理2.2）问题02：publicpartialclassChoosePLReason:CommonBaseForm2.3)问题03：介绍WindowsForms中的Syste
    
                    
    • 
                    
  • 通过C# 裁剪PDF页面
                        Eiceblue
C#.NETPDFc#pdf开发语言visualstudio
                        
    在处理PDF文档时，有时需要精确地裁剪页面以适应特定需求，比如去除广告、背景信息或者仅仅是为了简化文档内容。本文将指导如何使用免费.NET控件通过C#实现裁剪PDF页面。免费库FreeSpire.PDFfor.NET支持在.NET(C#,VB.NET,ASP.NET,.NETCore)程序中实现创建、操作、转换和打印PDF文档等操作。可以从以下链接下载产品包后手动添加引用，或者直接通过NuGet安
    
                    
    • 
                    
  • 【Unity基础】如何选择脚本编译方式Mono和IL2CPP？
                        tealcwu
Unity基础unity游戏引擎
                        
    Edit->ProjectSettings->Player在Unity中，ScriptingBackend决定了项目的脚本编译方式，即如何将C#代码转换为可执行代码。Unity提供了两种主要的ScriptingBackend选项：Mono和IL2CPP。它们之间的区别影响了项目的性能、平台支持、编译时间和调试体验。以下是两者的详细对比：1.Mono简介:Mono是Unity最早使用的脚本后端，基于
    
                    
    • 
                    
  • C# Tuple、ValueTuple
                        語衣
C#知识补充c#
                        
    栏目总目录TupleTuple是C#4.0引入的一个新特性，主要用于存储一个固定数量的元素序列，且这些元素可以具有不同的类型。Tuple是一种轻量级的数据结构，非常适合用于临时存储数据，而无需定义完整的类或结构体。优点简便性：可以快速创建一个包含多个不同类型数据的对象，而无需定义新的类或结构体。灵活性：元素数量和类型在编译时确定，但可以在不同上下文中重复使用不同元素的Tuple。缺点性能：作为引用
    
                    
    • 
                    
  • C# Linq语句用法大全以及Lambda表达式
                        一个小码码
c#linq开发语言.net
                        
    C#Linq语句用法大全以及Lambda表达式Linq：是一种用于数据查询和操作的语言集成查询（LanguageIntegratedQuery）技术。通过Linq，我们可以使用类似于SQL查询的方式来查询、筛选和操作各种类型的数据集合，包括数组、列表、集合、XML文档、数据库表等等。常见的有：LinqtoObjects：用于操作对象集合，例如数组、列表等。LinqtoXML：用于操作XML数据，支
    
                    
    • 
                    
  • C#中的LInq语句
                        weixin_30588907
c#数据库
                        
    语言集成查询(LINQ)是一组技术的名称，这些技术建立在将查询功能直接集成到C#语言（以及VisualBasic和可能的任何其他.NET语言）的基础上。借助于LINQ，查询现在已是高级语言构造，就如同类、方法、事件等等。对于编写查询的开发人员来说，LINQ最明显的“语言集成”部分是查询表达式。查询表达式是使用C#3.0中引入的声明性查询语法编写的。通过使用查询语法，您甚至可以使用最少的代码对数据源
    
                    
    • 
                    
  • C#的linq语句
                        木生火18624
C#开发
                        
    /查询表达式必须以form子句开头，以select或者group子句结束，在这两个子句之间，可以使用///where、orderby、join、let和其他的from子句本章要点用列表在对象上执行传统查询扩展方法LINQ查询操作符平行LNQ表达式树本章源代码下载地址(wrox.com)打开网页www.wrox.com/go/procsharp,单击DownloadCode选项卡即可下载本章源代码。
    
                    
    • 
                    
  • C# 多线程操作同一个文件，如何避免冲突
                        FlYFlOWERANDLEAF
c#开发语言
                        
    1使用lock经测试，依然存在线程冲突privatestaticobjectlocker=newobject();……lock(locker){stringbText=File.ReadAllText(FPath);returnbText;}……lock(locker){File.WriteAllText(FPath,aContent);}2使用ReaderWriterLockSlim经测试，依然
    
                    
    • 
                    
  • C#LINQ常用扩展语句
                        月落.
C#c#linqsolr
                        
    在C#中，LINQ提供了许多扩展方法，这些方法定义在System.Linq命名空间中。以下是一些常用的LINQ扩展方法：Where-过滤数据集合，返回满足条件的元素。varfilteredItems=collection.Where(item=>item.SomeProperty>10);Select-从数据集合中选择数据或创建新的投影。varprojectedItems=collection.S
    
                    
    • 
                    
  • source insight4.0中文乱码解决方法
                        鹿屿二向箔
c语言stm32keilmdk
                        
    Sourceinsight是强大、顺手的代码编辑器，它几乎支持所有的语言，包括：C，C++，C#，HTML等等，能够自动创建并维护它自己高性能的符号数据库，包括函数、全局变量、结构、类和工程源文件里定义的其它类型的符号，对于大工程的源码阅读非常方便。但是因为是国外软件，对中文支持不是很好，很多电脑安装使用都会出现注释乱码问题，很让人抓狂。网上很多人遇到类似的问题，也有很多解决方式，也有很多“终极解
    
                    
    • 
                    
  • C#基础知识-.NET，变量，容量单位，数据类型
                        yi碗汤园
c#开发语言
                        
    目录1.NET简介2.变量1）定义2）声明3）赋值3.容量单位4.数据类型1）整形(整数)2）非整型(小数)3）非数值型本篇文章来分享一下C#的基础知识，主要讲述一下变量和数据类型的相关知识。1.NET简介.NETdonet是Microsoft新一代多语言的开发平台，用于构建和运行应用程序。Unity借助Mono实现跨平台，核心是.NETFramework框架。2.变量1）什么是变量变量是用来存储
    
                    
    • 
                    
  • C# 在WPF中实现图表生成
                        A_nanda
WPF赏析c#wpf开发语言
                        
    在现代应用程序中，数据可视化是一个重要的功能，它可以帮助用户更直观地理解数据。在C#WPF（WindowsPresentationFoundation）中，有多种方式可以生成图表。以下是五种常见的方法，每种方法都有其独特的优势和局限。1.使用System.Windows.Shapes命名空间代码示例：<RectangleWidth="50"Height="50"Fill="Blue"Canva
    
                    
    • 
                    
  • C#中关闭窗口清除内容
                        Vae_Mars
AI对话中的其他知识c#开发语言
                        
    1.解释说明-窗口关闭时是可以执行函数的，可以做一部分事件处理-因为删除文件夹的方案不好做，所以改成清空文件夹内的内容2.程序示例publicMainWindow(){InitializeComponent();//检查窗口关闭this.Closing+=MainWindow_Closing;}//执行具体的方法privatevoidMainWindow_Closing(objectsender,
    
                    
    • 
                    
  • C#中Invoke的用法（）
                        世界太过浮夸
.netc#
                        
    转自：http://www.cnblogs.com/lsgsanxiao/p/5523282.htmlinvoke和begininvoke区别一直对invoke和begininvoke的使用和概念比较混乱，这两天看了些资料，对这两个的用法和原理有了些新的认识和理解。首先说下，invoke和begininvoke的使用有两种情况：control中的invoke、begininvoke。delegra
    
                    
    • 
                    
  • .NET常见面试题汇总
                        .Net Core 爱好者
.netc#
                        
    首先，汇总一共分为三部分：一是关于.NET技术的面试问题，二是关于.NET项目中的实际问题，三是历年出现过一些面试题汇总一、.NET技术面试问题请简述.NET中的装箱和拆箱。什么是泛型，以及它在.NET中的用途？请解释一下C#中的委托是什么，以及它们如何工作？什么是事件，如何使用它们？请解释一下C#中的特性(Attributes)及其应用场景。.NET中的异步编程模式有哪些？什么是LINQ，它在.
    
                    
    • 
                    
  • c# net8调用vc写的dll
                        wiseyao1219
c#开发语言dll
                        
    dll程序（vc,x86)头文件extern"C"int__declspec(dllexport)WINAPIadd(inta,intb);实现intWINAPIadd(inta,intb){returna+b;}c#/net8函数声明：[DllImport("dll/Dll1.dll",CallingConvention=CallingConvention.StdCall)]publicstat
    
                    
    • 
                    
  • c# json使用
                        wiseyao1219
c#json前端
                        
    安装包用NuGet安装包：Newtonsoft.Json对象转为Json字符串publicclassPerson{publicstringName{get;set;}publicintAge{get;set;}}Personperson=newPerson{Name="JohnDoe",Age=30};stringjson2=JsonConvert.SerializeObject(person);
    
                    
    • 
                                
  • jsonp 常用util方法
                                    hw1287789687
jsonpjsonp常用方法jsonp callback
                                    
    jsonp 常用java方法 
(1)以jsonp的形式返回:函数名(json字符串) 
/***
	 * 用于jsonp调用
	 * @param map : 用于构造json数据
	 * @param callback : 回调的javascript方法名
	 * @param filters : <code>SimpleBeanPropertyFilter theFilt
    
                                
    • 
                                
  • 多线程场景
                                    alafqq
多线程
                                    
    0 
能不能简单描述一下你在java web开发中需要用到多线程编程的场景？0 
对多线程有些了解，但是不太清楚具体的应用场景，能简单说一下你遇到的多线程编程的场景吗？ 
Java多线程 
2012年11月23日 15:41 Young9007 Young9007 
4 
0 0 4 
 
Comment添加评论关注(2) 
3个答案 按时间排序 按投票排序 
 
0 
0 
最典型的如： 
1、
    
                                
    • 
                                
  • Maven学习——修改Maven的本地仓库路径
                                    Kai_Ge
maven
                                    
          安装Maven后我们会在用户目录下发现.m2 文件夹。默认情况下，该文件夹下放置了Maven本地仓库.m2/repository。所有的Maven构件(artifact)都被存储到该仓库中，以方便重用。但是windows用户的操作系统都安装在C盘，把Maven仓库放到C盘是很危险的，为此我们需要修改Maven的本地仓库路径。 
  
 
    
                                
    • 
                                
  • placeholder的浏览器兼容
                                    120153216
placeholder
                                    
    【前言】 
自从html5引入placeholder后，问题就来了， 
不支持html5的浏览器也先有这样的效果， 
各种兼容，之前考虑，今天测试人员逮住不放， 
想了个解决办法，看样子还行，记录一下。 
  
【原理】 
不使用placeholder，而是模拟placeholder的效果， 
大概就是用focus和focusout效果。 
  
【代码】 
<scrip
    
                                
    • 
                                
  • debian_用iso文件创建本地apt源
                                    2002wmj
Debian
                                    
    1.将N个debian-506-amd64-DVD-N.iso存放于本地或其他媒介内，本例是放在本机/iso/目录下

2.创建N个挂载点目录  
如下： 
debian:~#mkdir –r /media/dvd1 
debian:~#mkdir –r /media/dvd2 
debian:~#mkdir –r /media/dvd3 
…. 
debian:~#mkdir –r /media
    
                                
    • 
                                
  • SQLSERVER耗时最长的SQL
                                    357029540
SQL Server
                                    
    对于DBA来说，经常要知道存储过程的某些信息： 
 
1.   执行了多少次 
 
2.   执行的执行计划如何 
 
3.   执行的平均读写如何 
 
4.   执行平均需要多少时间 
 
列名          &
    
                                
    • 
                                
  • com/genuitec/eclipse/j2eedt/core/J2EEProjectUtil
                                    7454103
eclipse
                                    
    今天eclipse突然报了com/genuitec/eclipse/j2eedt/core/J2EEProjectUtil 错误，并且工程文件打不开了，在网上找了一下资料，然后按照方法操作了一遍，好了，解决方法如下： 
 
错误提示信息： 
 
An error has occurred.See error log for more details. 
Reason: 
com/genuitec/
    
                                
    • 
                                
  • 用正则删除文本中的html标签
                                    adminjun
javahtml正则表达式去掉html标签
                                    
    使用文本编辑器录入文章存入数据中的文本是HTML标签格式，由于业务需要对HTML标签进行去除只保留纯净的文本内容，于是乎Java实现自动过滤。 
如下： 
public static String Html2Text(String inputString) {  
String htmlStr = inputString; // 含html标签的字符串
  String textSt
    
                                
    • 
                                
  • 嵌入式系统设计中常用总线和接口
                                    aijuans
linux 基础
                                    
                   嵌入式系统设计中常用总线和接口 
  
        任何一个微处理器都要与一定数量的部件和外围设备连接，但如果将各部件和每一种外围设备都分别用一组线路与CPU直接连接，那么连线
    
                                
    • 
                                
  • Java函数调用方式——按值传递
                                    ayaoxinchao
java按值传递对象基础数据类型
                                    
    Java使用按值传递的函数调用方式，这往往使我感到迷惑。因为在基础数据类型和对象的传递上，我就会纠结于到底是按值传递，还是按引用传递。其实经过学习，Java在任何地方，都一直发挥着按值传递的本色。 
  
首先，让我们看一看基础数据类型是如何按值传递的。 
  
public static void main(String[] args) {
		
	int a = 2;

    
                                
    • 
                                
  • ios音量线性下降
                                    bewithme
ios音量
                                    
    直接上代码吧 
  
//second 几秒内下降为0
- (void)reduceVolume:(int)second {
    KGVoicePlayer *player = [KGVoicePlayer defaultPlayer];
    
    if (!_flag) {
        _tempVolume = player.volume;
       
    
                                
    • 
                                
  • 与其怨它不如爱它
                                    bijian1013
选择理想职业规划
                                    
            抱怨工作是年轻人的常态，但爱工作才是积极的心态，与其怨它不如爱它。 
        一般来说，在公司干了一两年后，不少年轻人容易产生怨言，除了具体的埋怨公司“扭门”，埋怨上司无能以外，也有许多人是因为根本不爱自已的那份工作，工作完全成了谋生的手段，跟自已的性格、专业、爱好都相差甚远。 
  
    
                                
    • 
                                
  • 一边时间不够用一边浪费时间
                                    bingyingao
工作时间浪费
                                    
    一方面感觉时间严重不够用，另一方面又在不停的浪费时间。 
 
每一个周末，晚上熬夜看电影到凌晨一点，早上起不来一直睡到10点钟，10点钟起床，吃饭后玩手机到下午一点。 
精神还是很差，下午像一直野鬼在城市里晃荡。 
 
 
为何不尝试晚上10点钟就睡，早上7点就起，时间完全是一样的，把看电影的时间换到早上，精神好，气色好，一天好状态。 
控制让自己周末早睡早起，你就成功了一半。 
 
有多少个工作
    
                                
    • 
                                
  • 【Scala八】Scala核心二：隐式转换
                                    bit1129
scala
                                    
    Implicits work like this: if you call a method on a Scala object, and the Scala compiler does not see a definition for that method in the class definition for that object, the compiler will try to con
    
                                
    • 
                                
  • sudoku slover in Haskell (2)
                                    bookjovi
haskellsudoku
                                    
    继续精简haskell版的sudoku程序，稍微改了一下，这次用了8行，同时性能也提高了很多，对每个空格的所有解不是通过尝试算出来的，而是直接得出。 
  
board = [0,3,4,1,7,0,5,0,0,
         0,6,0,0,0,8,3,0,1,
         7,0,0,3,0,0,0,0,6,
         5,0,0,6,4,0,8,0,7,

    
                                
    • 
                                
  • Java-Collections Framework学习与总结-HashSet和LinkedHashSet
                                    BrokenDreams
linkedhashset
                                    
            本篇总结一下两个常用的集合类HashSet和LinkedHashSet。 
        它们都实现了相同接口java.util.Set。Set表示一种元素无序且不可重复的集合；之前总结过的java.util.List表示一种元素可重复且有序
    
                                
    • 
                                
  • 读《研磨设计模式》-代码笔记-备忘录模式-Memento
                                    bylijinnan
java设计模式
                                    
    声明： 本文只为方便我个人查阅和理解，详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/ 
 
 

import java.util.ArrayList;
import java.util.List;



/*
 * 备忘录模式的功能是，在不破坏封装性的前提下，捕获一个对象的内部状态，并在对象之外保存这个状态，为以后的状态恢复作“备忘”

    
                                
    • 
                                
  • 《RAW格式照片处理专业技法》笔记
                                    cherishLC
PS
                                    
    注意，这不是教程！仅记录楼主之前不太了解的 
 
 一、色彩（空间）管理 
作者建议采用ProRGB（色域最广），但camera raw中设为ProRGB，而PS中则在ProRGB的基础上，将gamma值设为了1.8（更符合人眼） 
注意：bridge、camera raw怎么设置显示、输出的颜色都是正确的（会读取文件内的颜色配置文件），但用PS输出jpg文件时，必须先用Edit->conv
    
                                
    • 
                                
  • 使用 Git 下载 Spring 源码 编译 for Eclipse
                                    crabdave
eclipse
                                    
    使用 Git 下载 Spring 源码 编译 for Eclipse 
  
1、安装gradle，下载 http://www.gradle.org/downloads 
配置环境变量GRADLE_HOME，配置PATH  %GRADLE_HOME%/bin，cmd，gradle -v 
  
2、spring4 用jdk8 下载 https://jdk8.java.
    
                                
    • 
                                
  • mysql连接拒绝问题
                                    daizj
mysql登录权限
                                    
    mysql中在其它机器连接mysql服务器时报错问题汇总 
 
一、[running][email protected]:~$mysql -uroot -h 192.168.9.108 -p   //带-p参数，在下一步进行密码输入 
Enter password:    //无字符串输入 
ERROR 1045 (28000): Access 
    
                                
    • 
                                
  • Google Chrome 为何打压 H.264
                                    dsjt
applehtml5chromeGoogle
                                    
    Google 今天在 Chromium 官方博客宣布由于 H.264 编解码器并非开放标准，Chrome 将在几个月后正式停止对 H.264 视频解码的支持，全面采用开放的 WebM 和 Theora 格式。 
 
Google 在博客上表示，自从 WebM 视频编解码器推出以后，在性能、厂商支持以及独立性方面已经取得了很大的进步，为了与 Chromium 现有支持的編解码器保持一致，Chrome
    
                                
    • 
                                
  • yii 获取控制器名 和方法名
                                    dcj3sjt126com
yiiframework
                                    
    1. 获取控制器名 
在控制器中获取控制器名:  $name = $this->getId(); 
在视图中获取控制器名:    $name = Yii::app()->controller->id;  
  
2. 获取动作名  
在控制器beforeAction()回调函数中获取动作名:  $name = 
    
                                
    • 
                                
  • Android知识总结（二）
                                    come_for_dream
android
                                    
    明天要考试了，速速总结如下 
  
1、Activity的启动模式 
       standard：每次调用Activity的时候都创建一个（可以有多个相同的实例，也允许多个相同Activity叠加。） 
       singleTop：可以有多个实例，但是不允许多个相同Activity叠加。即，如果Ac
    
                                
    • 
                                
  • 高洛峰收徒第二期：寻找未来的“技术大牛” ——折腾一年，奖励20万元
                                    gcq511120594
工作项目管理
                                    
    高洛峰，兄弟连IT教育合伙人、猿代码创始人、PHP培训第一人、《细说PHP》作者、软件开发工程师、《IT峰播》主创人、PHP讲师的鼻祖！ 
首期现在的进程刚刚过半，徒弟们真的很棒，人品都没的说，团结互助，学习刻苦，工作认真积极，灵活上进。我几乎会把他们全部留下来，现在已有一多半安排了实际的工作，并取得了很好的成绩。等他们出徒之日，凭他们的能力一定能够拿到高薪，而且我还承诺过一个徒弟，当他拿到大学毕
    
                                
    • 
                                
  • linux expect
                                    heipark
expect
                                    
    1. 创建、编辑文件go.sh 
  
#!/usr/bin/expect

spawn sudo su admin

expect  "*password*" { send "13456\r\n" }

interact  
   2. 设置权限 
   chmod u+x go.sh   3.
    
                                
    • 
                                
  • Spring4.1新特性——静态资源处理增强
                                    jinnianshilongnian
spring 4.1
                                    
    目录 
Spring4.1新特性——综述 
Spring4.1新特性——Spring核心部分及其他 
Spring4.1新特性——Spring缓存框架增强 
Spring4.1新特性——异步调用和事件机制的异常处理 
Spring4.1新特性——数据库集成测试脚本初始化 
Spring4.1新特性——Spring MVC增强 
Spring4.1新特性——页面自动化测试框架Spring MVC T
    
                                
    • 
                                
  • idea ubuntuxia 乱码
                                    liyonghui160com

                                    
        
1.首先需要在windows字体目录下或者其它地方找到simsun.ttf 这个 字体文件。 
2.在ubuntu 下可以执行下面操作安装该字体： 
sudo mkdir /usr/share/fonts/truetype/simsun
sudo cp simsun.ttf  /usr/share/fonts/truetype/simsun
fc-cache -f -v 

    
                                
    • 
                                
  • 改良程序的11技巧
                                    pda158
技巧
                                    
    有很多理由都能说明为什么我们应该写出清晰、可读性好的程序。最重要的一点，程序你只写一次，但以后会无数次的阅读。当你第二天回头来看你的代码 时，你就要开始阅读它了。当你把代码拿给其他人看时，他必须阅读你的代码。因此，在编写时多花一点时间，你会在阅读它时节省大量的时间。 
  
让我们看一些基本的编程技巧： 
  
 
 尽量保持方法简短 
 永远永远不要把同一个变量用于多个不同的
    
                                
    • 
                                
  • 300个涵盖IT各方面的免费资源（下）——工作与学习篇
                                    shoothao
创业免费资源学习课程远程工作
                                    
    工作与生产效率: 
  
 
 A. 背景声音 
 
 
  Noisli:背景噪音与颜色生成器。 
  Noizio:环境声均衡器。 
  Defonic:世界上任何的声响都可混合成美丽的旋律。 
  Designers.mx:设计者为设计者所准备的播放列表。 
  Coffitivity:这里的声音就像咖啡馆里放的一样。 
 
 
 B. 避免注意力分散 
 
 
  Self Co
    
                                
    • 
                                
  • 深入浅出RPC
                                    uule
rpc
                                    
    深入浅出RPC-浅出篇 
深入浅出RPC-深入篇 
  
RPC 
Remote Procedure Call Protocol 
远程过程调用协议 
  
它是一种通过网络从远程计算机程序上请求服务，而不需要了解底层网络技术的协议。RPC协议假定某些传输协议的存在，如TCP或UDP，为通信程序之间携带信息数据。在OSI网络通信模型中，RPC跨越了传输层和应用层。RPC使得开发
    
                                
    •