决策树算法--CART分类树算法

ID3和C4.5算法，生成的决策树是多叉树，只能处理分类不能处理回归。而CART（classification and regression tree）分类回归树算法，既可用于分类也可用于回归。 分类树的输出是样本的类别， 回归树的输出是一个实数。

CART算法步骤

1. 特征选择；
2. 递归建立决策树；
3. 决策树剪枝；

CART分类树算法

ID3中使用了信息增益选择特征，增益大优先选择。C4.5中，采用信息增益率选择特征，减少因特征值多导致信息增益大的问题。CART分类树算法使用基尼系数选择特征，基尼系数代表了模型的不纯度，基尼系数越小，不纯度越低，特征越好。这和信息增益（率）相反。

基尼系数

数据集D的纯度可用基尼值来度量
$$\begin{array}{rl}Gini(D)& =\sum _{i=1}^{n}p(x_i)\ast (1-p(x_i))\\ & =1-\sum _{i=1}^n{p(x_i)}^2\end{array}$$
其中，$p(x_i)$是分类$x_i$出现的概率，n是分类的数目。Gini(D)反映了从数据集D中随机抽取两个样本，其类别标记不一致的概率。因此，Gini(D)越小，则数据集D的纯度越高。

对于样本D，个数为|D|，根据特征A 是否取某一可能值a，把样本D分成两部分$D_1和D_2$ 。所以CART分类树算法建立起来的是二叉树，而不是多叉树。
$$D_1=\{(x,y)\in D|A(x)=a\},D_2=D-D_1$$
在属性A的条件下，样本D的基尼系数定义为
$$GiniIndex(D|A=a)=\frac{|D_1|}{|D|}Gini(D_1)+\frac{|D_2|}{|D|}Gini(D_2)$$

对连续特征和离散特征的处理

连续特征

与C4.5思想相同，都是将连续的特征离散化。区别在选择划分点时，C4.5是信息增益率，CART是基尼系数。

具体思路：

1. m个样本的连续特征A有m个值，从小到大排列$a_1,a_2,...,a_m$，则CART取相邻两样本值的平均数做划分点，一共有m-1个，其中第i个划分点Ti表示为：$T_i=(a_i+a_{i+1})/2$。
2. 分别计算以这m-1个点作为二元分类点时的基尼系数。选择基尼系数最小的点为该连续特征的二元离散分类点。比如取到的基尼系数最小的点为$a_t$，则小于$a_t$的值为类别1，大于$a_t$的值为类别2，这样就做到了连续特征的离散化。

注意的是，与ID3、C4.5处理离散属性不同的是，如果当前节点为连续属性，则该属性在后面还可以参与子节点的产生选择过程。

离散特征

思路：不停的二分离散特征。

在ID3、C4.5，特征A被选取建立决策树节点，如果它有3个类别A1,A2,A3，我们会在决策树上建立一个三叉点，这样决策树是多叉树，而且离散特征只会参与一次节点的建立。

CART采用的是不停的二分，且一个特征可能会参与多次节点的建立。CART会考虑把特征A分成$\{A_1\}$和$\{A_2,A_3\}、\{A_2\}和\{A_1,A_3\}、\{A_3\}和\{A_1,A_2\}$三种情况，找到基尼系数最小的组合，比如$\{A_2\}$和$\{A_1,A_3\}$，然后建立二叉树节点，一个节点是$A_2$对应的样本，另一个节点是对$\{A_1,A_3\}$对应的样本。由于这次没有把特征A的取值完全分开，后面还有机会对子节点继续选择特征A划分$A_1$和$A_3$。

例子

数据集的属性有3个，分别是有房情况，婚姻状况和年收入，其中有房情况和婚姻状况是离散的取值，而年收入是连续的取值。拖欠贷款者属于分类的结果。

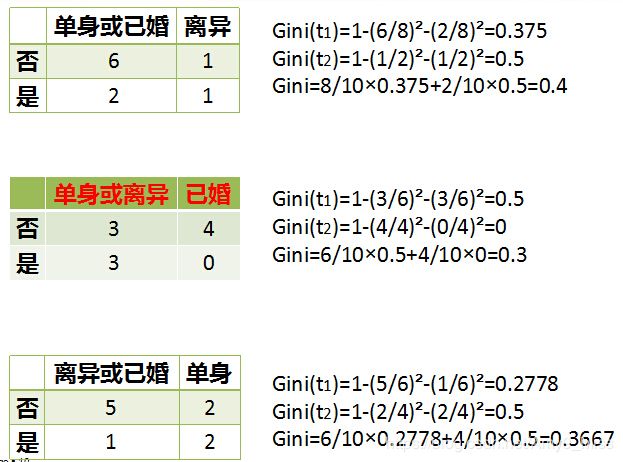
对于有房情况这个属性，它是离散型数据，那么按照它划分后的Gini系数计算如下

对于婚姻状况属性，它也是离散型数据，它的取值有3种，按照每种属性值分裂后Gini系数计算如下

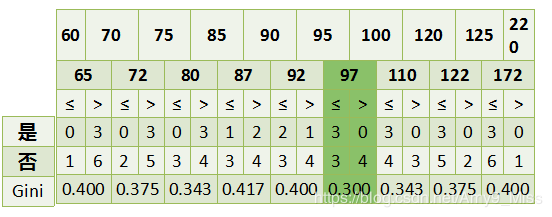
年收入属性，它的取值是连续的，那么连续的取值采用分裂点进行分裂。如下

根据这样的分裂规则CART算法就能完成建树过程 。

建立CART分类树步骤

输入：训练集D，基尼系数的阈值，切分的最少样本个数阈值

输出：分类树T

算法从根节点开始，用训练集递归建立CART分类树。

1. 对于当前节点的数据集为D，如果样本个数小于阈值或没有特征，则返回决策子树，当前节点停止递归；
2. 计算样本集D的基尼系数，如果基尼系数小于阈值，则返回决策树子树，当前节点停止递归 ；
3. 计算当前节点现有各个特征的各个值的基尼指数，
4. 在计算出来的各个特征的各个值的基尼系数中，选择基尼系数最小的特征A及其对应的取值a作为最优特征和最优切分点。 然后根据最优特征和最优切分点，将本节点的数据集划分成两部分$D_1$和$D_2$，同时生成当前节点的两个子节点，左节点的数据集为$D_1$，右节点的数据集为$D_2$。
5. 对左右的子节点递归调用1-4步，生成CART分类树；

对生成的CART分类树做预测时，假如测试集里的样本落到了某个叶子节点，而该节点里有多个训练样本。则该测试样本的类别为这个叶子节点里概率最大的类别。

剪枝

当分类回归树划分得太细时，会对噪声数据产生过拟合，因此要通过剪枝来解决。剪枝又分为前剪枝和后剪枝，前剪枝是指在构造树的过程中就知道哪些节点可以剪掉 。 后剪枝是指构造出完整的决策树之后再来考查哪些子树可以剪掉。

在分类回归树中可以使用的后剪枝方法有多种，比如：代价复杂性剪枝、最小误差剪枝、悲观误差剪枝等等。这里只介绍代价复杂性剪枝法。

对于分类回归树中的每一个非叶子节点计算它的表面误差率增益值α
$$\alpha =\frac{C(t)-C(T_t)}{|T_t|-1}$$
$|T_t|$:子树中包含的叶子节点个数

C(t)：以t为单节点树的误差代价，该节点被剪枝
$$C(t)=r(t)\ast p(t)$$
r(t)：节点t的误差率

p(t)：节点t上的数据占所有户数的比例

$C(T_t)$是以t为根节点的子树$T_t$的误差代价，如果该节点不被剪枝， 它等于子树$T_t$上所有叶子节点的误差代价之和。

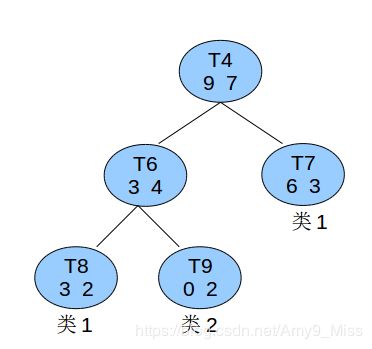
比如有个非叶子节点T4如图所示：

已知所有的数据总共有60条，则节点T4的节点误差代价为：
$$C(t)=r(t)\ast p(t)=\frac{7}{16}\ast \frac{16}{60}=\frac{7}{60}$$
子树误差代价为：
$$C(T_t)=\sum C(i)=\frac{2}{5}\ast \frac{5}{60}+\frac{0}{2}\ast \frac{2}{60}+\frac{3}{9}\ast \frac{9}{60}=\frac{5}{60}$$
以T4为根节点的子树上叶子节点有3个，则
$$\alpha =\frac{7/60-5/60}{3-1}=\frac{1}{60}$$
找到$\alpha$值最小的非叶子节点，令其左、右子节点为NULL。当多个非叶子节点的α值同时达到最小时，取$|T_t|$最大的进行剪枝。

总结

算法	树结构	支持模型	特征选择	连续值处理	缺失值处理	剪枝
ID3	多叉树	分类	信息增益	不支持	不支持	不支持
C4.5	多叉树	分类	信息增益率	支持	支持	支持
CART	二叉树	分类、回归	基尼系数、平方误差和	支持	支持	支持

相关链接

书籍：《机器学习实战》、周志华的西瓜书《机器学习》

例子参考链接

剪枝参考链接

ID3算法

C4.5算法

CART回归树算法