CRF实现中文词性标注(1)——原理说明
写在前边
po上看到的一个大佬的博文,这篇博客也是学习大佬的文章。
文中图片也来自于参考博文。
参考链接:
CRF、有向图、无向图
大佬的图模型
大佬的CRF讲解
我的知乎专栏,小白要努力了哦
python 实现CRF,并用于序列标注参考代码
python-crf
simple_crf

图模型
背景
Naive Bayes
P ( X ∣ y ) = p ( x 1 ∣ y ) p ( x 2 ∣ y ) . . . . p ( x 3 ∣ y ) P(X|y) = p(x1|y)p(x2|y)....p(x3|y) P(X∣y)=p(x1∣y)p(x2∣y)....p(x3∣y)
如果用图中的结点表示变量,边表示变量之间的关系,那么朴素贝叶斯就可以用下边的图表示。

最大熵模型
P ( y ∣ x ) = e x p ( ∑ i = 1 n w i f i ( x , y ) ) Z w ( x ) P(y|x) = \frac{exp(\sum_{i=1}^{n} w_{i} f_{i}(x,y ))}{Z_{w}(x)} P(y∣x)=Zw(x)exp(∑i=1nwifi(x,y))
Naive Bayes中使用的是条件概率,而最大熵中使用的是特征函数,二者的区别在于条件概率是有向的,而特征函数是无向的,所以有了将图模型分为有向图和无向图。
无向图
《统计学习方法》中定义

概率无向图中的联合概率分布P(Y)可以写作是图中所有最大团C上的函数
ψ c ( Y c ) \psi_{c}(Y_{c}) ψc(Yc)的乘积形式
P ( Y ) = 1 Z ∏ c ( ψ c ( y c ) ) Z = ∑ ∏ c ( ψ c ( y c ) \begin{aligned} P(Y) &= \frac{1}{Z} \prod_{c} (\psi_{c} (y_{c})) \\ Z &= \sum \prod_{c} (\psi_{c} (y_{c}) \end{aligned} P(Y)Z=Z1c∏(ψc(yc))=∑c∏(ψc(yc)
比如:

有向图
DAG(Directed acyclic graph),有向无环图。
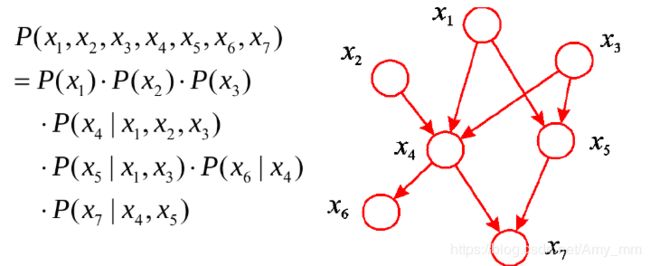
DAG模型可以理解为联合概率等于每个节点在其父节点下的条件概率的累乘。
P ( Y ) = ∏ s = 1 S p ( y s ∣ Y π s ) P(Y) = \prod_{s = 1}^{S} p(y_{s} \mid Y_{\pi_{s}}) P(Y)=s=1∏Sp(ys∣Yπs)
CRF

CRF(conditional Random Fields),条件随机场是一种无向图,是在给定随机变量X下,随机变量Y的马尔科夫随机场。
主要讨论用在序列标注中的线性链CRF。条件概率模型P(Y | X)中Y是输出变量,也称为状态序列或者标记序列或者隐序列,也就是未知的;X是观测序列,POS中的单词就是观测序列,词性就是状态序列。
- CRF的学习问题:
用极大似然或者正则化的极大似然求得条件概率模型P(Y|X) - 预测问题:
输入序列x, 求解概率P(y|x) 最大的y序列
线性链CRF
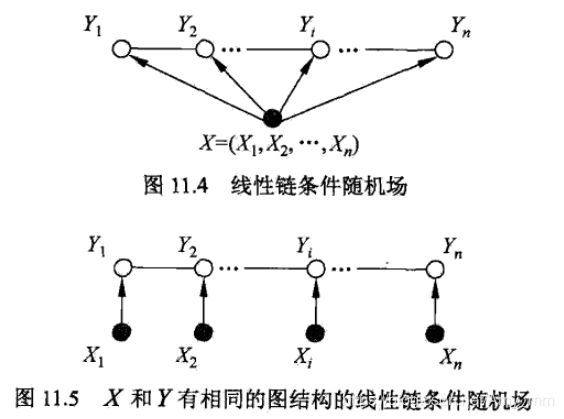
x = (X1,X2,…Xn), Y = (Y1,Y2,…Yn)均为线性链表示的随机序列,在给定X的情况下,P(Y|X) 构成CRF,也就是满足马尔科夫性:
P ( Y i ∣ X , Y 1 , . . Y i − 1 , Y i + 1 , . . Y n ) = P ( Y i ∣ X , Y i − 1 , Y i + 1 ) P(Y_{i} \mid X,Y_{1}, ..Y_{i-1},Y_{i+1},..Y_{n}) = P(Y_{i} \mid X, Y_{i-1},Y_{i+1}) P(Yi∣X,Y1,..Yi−1,Yi+1,..Yn)=P(Yi∣X,Yi−1,Yi+1)
称P(Y|X)构成线性链条件随机场。
参数化形式
P ( y ∣ x ) = 1 Z ( x ) e x p ( ∑ i , k λ k t k ( y i , y i − 1 , x , i ) + ∑ i , l μ l s l ( y i , x , i ) ) Z ( x ) = ∑ y e x p ( ∑ i , k λ k t k ( y i , y i − 1 , x , i ) + ∑ i , l μ l s l ( y i , x , i ) ) \begin{aligned} P(y \mid x) &= \frac{1}{Z(x)} exp(\sum_{i,k} \lambda_{k} t_{k}(y_{i}, y_{i-1}, x,i) + \sum_{i,l} \mu_{l} s_{l}(y_{i}, x, i)) \\ Z(x) &= \sum_{y} exp(\sum_{i,k} \lambda_{k} t_{k}(y_{i}, y_{i-1}, x,i) + \sum_{i,l} \mu_{l} s_{l}(y_{i}, x, i)) \end{aligned} P(y∣x)Z(x)=Z(x)1exp(i,k∑λktk(yi,yi−1,x,i)+i,l∑μlsl(yi,x,i))=y∑exp(i,k∑λktk(yi,yi−1,x,i)+i,l∑μlsl(yi,x,i))
其中t是定义在边上的特征函数,称为转移特征,依赖于前一个和当前位置;s是定义在节点上的特征函数,称为状态特征,只依赖于当前位置; λ , μ \lambda,\mu λ,μ是对应的权重。t和s都依赖于位置,所以都是局部特征,通常取值为0或者1,满足特征函数取值1,不满足取值0。
CRF完全由特征函数和权值决定。
简化形式
参数化形式中的CRF的特征函数与位置有关,也就是局部特征。CRF的简化形式是对同一个特征,将其在各个位置求和,这样就把局部特征转化为了全局特征。
首先定义K1个转移特征和K2个状态特征。
- 特征函数f定义为:
f k ( y i − 1 , y i , x , i ) = { t k ( y i − 1 , y i , x , i ) k = 1 , 2 , 3.. K 1 s l ( y i , x , i ) k = k 1 + l , l = 1 , 2 , . . K 2 } f_{k}(y_{i-1},y_{i}, x, i ) = \begin{Bmatrix} t_{k}(y_{i-1},y_{i}, x, i ) \quad & k = 1,2,3..K1\\ s_{l}(y_{i}, x, i ) \quad &k = k1 + l, l = 1,2,..K2 \end{Bmatrix} fk(yi−1,yi,x,i)={tk(yi−1,yi,x,i)sl(yi,x,i)k=1,2,3..K1k=k1+l,l=1,2,..K2} - 在各个位置求和:
f k ( x , y ) = ∑ i = 1 n f k ( y i − 1 , y i , x , i ) k = 1 , 2... K ( K = k 1 + K 2 ) f_{k} (x,y) = \sum_{i=1}^{n} f_{k}(y_{i-1},y_{i}, x, i ) \quad k =1,2... K \quad (K=k1 + K2) fk(x,y)=i=1∑nfk(yi−1,yi,x,i)k=1,2...K(K=k1+K2) - w表示权值
w k = { λ k k = 1 , 2 , . . k 1 μ l k = k 1 + l , l = 1 , 2 , . . k 2 } w_{k} = \begin{Bmatrix} \lambda_{k} & k = 1,2,.. k1 \\ \mu_{l} & k = k1+l, l= 1,2,.. k2 \end{Bmatrix} wk={λkμlk=1,2,..k1k=k1+l,l=1,2,..k2} - 得到CRF的简化形式为
P ( y ∣ x ) = 1 Z ( x ) e x p ∑ k = 1 K w k f k ( x , y ) Z ( x ) = ∑ e x p ( ∑ k = 1 K w k f k ( x , y ) ) P(y \mid x) = \frac{1}{Z(x)} exp\sum_{k=1}^{K} w_{k} f_{k}(x,y) \\ Z(x) = \sum exp( \sum_{k=1}^{K} w_{k} f_{k}(x,y)) P(y∣x)=Z(x)1expk=1∑Kwkfk(x,y)Z(x)=∑exp(k=1∑Kwkfk(x,y))
写成向量形式:
w = ( w 1 , w 2 , . . w K ) T F ( y , x ) = ( f 1 ( x , y ) , . . . f k ( x , y ) T ) p ( y ∣ x ) = e x p ( w ⋅ F ( x , y ) ) Z w ( x ) w = (w_{1},w_{2},..w_{K})^{T} \\ F(y,x) = (f_{1}(x,y),...f_{k}(x,y) ^{T}) p(y | x) = \frac{exp(w \cdot F(x,y))}{Z_{w}(x)} w=(w1,w2,..wK)TF(y,x)=(f1(x,y),...fk(x,y)T)p(y∣x)=Zw(x)exp(w⋅F(x,y))
矩阵形式
参考链接:
CRF矩阵形式参考链接
太懒了,懒得打矩阵形式了···

CRF的矩阵形式类似于HMM中的转移矩阵,就是 y i − 1 y_{i-1} yi−1的m种状态到 y i y_{i} yi的m种状态的转移概率。
举个例子说明:


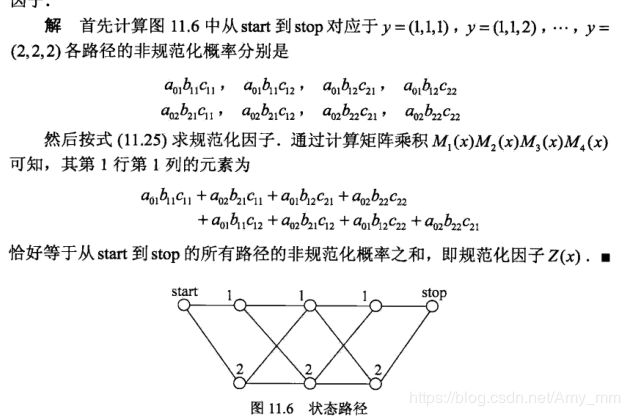
矩阵推导过程:
各个矩阵累乘正好是从start到stop所有路径的非规范化概率之和。
CRF的三个问题
同HMM,CRF也存在概率计算、学习和预测问题。
- 概率计算问题:给定条件随机场P(Y|X),输入序列x和输出序列y,计算条件概率P(Yi=yi|x)和P(Yi−1=yi−1,Yi=yi|x)和相应的数学期望。
- 学习问题:给定训练数据集,估计条件随机场模型参数,也就是用极大似然法的方法估计参数。
- 预测问题:给定条件随机场P(Y|X)和输入序列(观测序列)x,求条件概率最大的输出序列(标记序列)y∗。
概率计算问题
前向 后向向量
给定CRF模型P(Y|X) ,输入序列x,输出序列y,计算条件概率 p ( y i ∣ x ) p(y_{i} \mid x) p(yi∣x)和 p ( y i − 1 , y i ∣ x ) p(y_{i-1}, y_{i} \mid x) p(yi−1,yi∣x)。
可以看出CRF是直接计算条件概率也就是CRF是判别式模型,HMM是由联合概率计算,先由状态 i 生成下一个状态 i+1, 在由状态 i+1 生成i+1状态下的输出, 是生成式模型。
- 前向 向量
对于i = 0,1,2,…n+1,定义前向向量 α i ( x ) \alpha_{i}(x) αi(x)为:
α 0 ( y ∣ x ) = { 1 , y = s t a r t 0 , e l s e } \alpha_{0} (y| x) = \begin{Bmatrix} 1, & y = start \\ 0, & else \end{Bmatrix} α0(y∣x)={1,0,y=startelse}
前向向量的递推
α i T ( y i ∣ x ) = α i − 1 T ( y i − 1 ∣ x ) M i ( y i − 1 , y i ∣ x ) i = 1 , 2 , . . . n + 1 \alpha_{i} ^{T} (y_{i} \mid x)= \alpha_{i-1} ^{T} (y_{i-1} \mid x) M_{i}(y_{i-1}, y_{i} \mid x) \quad i=1,2,...n+1 αiT(yi∣x)=αi−1T(yi−1∣x)Mi(yi−1,yi∣x)i=1,2,...n+1
或者表示为
α i T ( x ) = α i − 1 T ( x ) M i ( x ) i = 1 , 2 , . . . n + 1 \alpha_{i}^{T} (x)= \alpha_{i-1} ^{T}(x) M_{i}(x) \quad i=1,2,...n+1 αiT(x)=αi−1T(x)Mi(x)i=1,2,...n+1
α i T ( y i ∣ x ) \alpha_{i}^{T} (y_{i} \mid x) αiT(yi∣x)表示从0到i位置的标记序列的非规范化概率。
- 后向向量
同理可定义后向向量
对于i = 0,1,2,…n+1,定义前向向量 α i ( x ) \alpha_{i}(x) αi(x)为:
β n + 1 ( y n + 1 ∣ x ) = { 1 , y n + 1 = s t o p 0 , e l s e } \beta_{n+1} (y_{n+1}| x) = \begin{Bmatrix} 1, & y_{n+1} = stop \\ 0, & else \end{Bmatrix} βn+1(yn+1∣x)={1,0,yn+1=stopelse}
后向向量的递推
β i ( y i ∣ x ) = M i + 1 ( y i , y i + 1 ∣ x ) β i + 1 ( y i + 1 ∣ x ) i = 1 , 2 , . . . n + 1 \beta_{i} (y_{i} \mid x)= M_{i + 1}(y_{i}, y_{i+1} \mid x) \beta_{i+1} (y_{i+1} \mid x) \quad i=1,2,...n+1 βi(yi∣x)=Mi+1(yi,yi+1∣x)βi+1(yi+1∣x)i=1,2,...n+1
或者表示为
β i ( x ) = M i + 1 ( x ) β i + 1 ( x ) i = 1 , 2 , . . . n + 1 \beta_{i}(x)= M_{i+1}(x) \beta_{i+1} (x) \quad i=1,2,...n+1 βi(x)=Mi+1(x)βi+1(x)i=1,2,...n+1
β i ( y i ∣ x ) \beta_{i} (y_{i} \mid x) βi(yi∣x)表示从 i+1 到 n位置的标记序列的非规范化概率。
概率计算
其实我不是太懂这个具体的怎么就前向乘以后向了
P ( Y i = y i ∣ x ) = α i T ( y i ∣ x ) β i ( y i ∣ x ) Z ( x ) P( Y_{i} = y_{i} \mid x) = \frac{\alpha_{i} ^{T}(y_{i} \mid x) \beta_{i}(y_{i} \mid x)}{Z(x)} P(Yi=yi∣x)=Z(x)αiT(yi∣x)βi(yi∣x)
Z ( x ) = α n ( x ) T ⋅ 1 = 1 T ⋅ β 1 ( x ) Z(x) = \alpha_{n}(x)^{T} \cdot 1 =1^{T} \cdot \beta_{1}(x) Z(x)=αn(x)T⋅1=1T⋅β1(x)
P ( Y i = y i , Y i − 1 = y i − 1 ∣ x ) = α i − 1 T ( y i − 1 ∣ x ) M i ( y i − 1 , y i ∣ x ) β i ( y i ∣ x ) Z ( x ) P(Y_{i} = y_{i}, Y_{i-1} = y_{i-1} \mid x) = \frac{\alpha_{i-1} ^{T}(y_{i-1} \mid x) M_{i}(y_{i-1}, y_{i} \mid x) \beta_{i}(y_{i} \mid x)}{Z(x)} P(Yi=yi,Yi−1=yi−1∣x)=Z(x)αi−1T(yi−1∣x)Mi(yi−1,yi∣x)βi(yi∣x)
学习问题
CRF 是定义在时序数据上的对数线性模型,学习方法包括极大似然估计和正则化的极大似然估计,具体的优化算法实现包括改进的迭代尺度算法、拟牛顿法和梯度下降法。
- 改进的迭代尺度算法
已知训练数据集,可以知道经验概率分布P(X,Y),然后通过极大化训练数据的对数似然函数学习模型参数。
经验分布
p ^ ( x , y ) = c o u n t ( x , y ) N p ^ ( x ) = c o u n t ( x ) N \hat p(x,y) = \frac{count(x,y)}{N} \\ \hat p(x) = \frac{count(x)}{N} p^(x,y)=Ncount(x,y)p^(x)=Ncount(x)
对数似然函数
L ( w ) = L ( P w ) = l o g ∏ x , y P w ( y ∣ x ) p ^ ( x , y ) = ∑ x , y p ^ ( x , y ) l o g p w ( y ∣ x ) \begin{aligned} L(w) & = L(P_{w}) \\ & = log \prod_{x,y}P_{w}(y \mid x) ^{\hat p(x,y)} \\ & = \sum_{x,y}\hat p(x,y) log p_{w} (y \mid x) \end{aligned} L(w)=L(Pw)=logx,y∏Pw(y∣x)p^(x,y)=x,y∑p^(x,y)logpw(y∣x)
p w ( y ∣ x ) = e x p ∑ k ( w k f k ( y , x ) ) z w ( x ) p_{w}(y \mid x) = \frac{exp \sum_{k} (w_{k} f_{k} (y,x))} {z_{w}(x)} pw(y∣x)=zw(x)exp∑k(wkfk(y,x))
代入可得
L w = ∑ x , y p ^ ( x , y ) l o g p w ( y ∣ x ) = ∑ x , y p ^ ( x , y ) ∑ k w k f k ( y , x ) − ∑ x , y p ^ ( x , y ) l o g Z w ( x ) = ∑ k ∑ i w k f k ( y i , x i ) − ∑ i l o g Z w ( x x i ) \begin{aligned} L_{w} & = \sum_{x,y}\hat p(x,y) log p_{w} (y \mid x) \\ & = \sum_{x,y}\hat p(x,y) \sum_{k} w_{k}f_{k}(y,x) - \sum_{x,y}\hat p(x,y) log Z_{w}(x) \\ & = \sum_{k} \sum_{i} w_{k} f_{k}(y_{i}, x_{i}) - \sum_{i} logZ_{w}(x_{x_{i}}) \end{aligned} Lw=x,y∑p^(x,y)logpw(y∣x)=x,y∑p^(x,y)k∑wkfk(y,x)−x,y∑p^(x,y)logZw(x)=k∑i∑wkfk(yi,xi)−i∑logZw(xxi)
改进的迭代尺度算法是通过迭代的方法不断优化对数似然函数改变量的下界,达到 极大化似然函数的目的。具体可以参考下图,截图至《统计学习方法》。
- 当前参数向量w = (w1, w2, …wk) ,
- 参数向量增量为 δ = ( δ 1 , δ 2 . . . δ k ) \delta = (\delta_{1}, \delta_{2} ...\delta_{k}) δ=(δ1,δ2...δk),
- 更新参数 w = w + δ w = w + \delta w=w+δ
转移特征更新
E p ^ [ t k ] = ∑ x , y p ^ ( x , y ) ∑ i t k ( y i − 1 , y i , x , i ) = ∑ x , y p ^ ( x ) p ( y ∣ x ) ∑ i t k ( y i − 1 , y i , x , i ) e x p ( δ k F ( x , y ) ) k = 1 , 2 , 3.. K 1 \begin{aligned} E_{\hat p} [t_{k}] &= \sum _{x,y} \hat p(x,y) \sum_{i} t_{k}(y_{i-1}, y_{i}, x,i) \\ & = \sum _{x,y }\hat p(x) p(y \mid x) \sum_{i} t_{k}(y_{i-1}, y_{i}, x,i) exp(\delta_{k} F(x,y)) \\ k &= 1,2,3..K1 \end{aligned} Ep^[tk]k=x,y∑p^(x,y)i∑tk(yi−1,yi,x,i)=x,y∑p^(x)p(y∣x)i∑tk(yi−1,yi,x,i)exp(δkF(x,y))=1,2,3..K1
状态特征更新
E p ^ [ s l ] = ∑ x , y p ^ ( x , y ) ∑ i s l ( y i , x , i ) = ∑ x , y p ^ ( x ) p ( y ∣ x ) ∑ i s l ( y i , x , i ) e x p ( δ k + l F ( x , y ) ) l = 1 , 2 , 3.. K 2 \begin{aligned} E_{\hat p} [s_{l}] &= \sum _{x,y} \hat p(x,y) \sum_{i} s_{l}( y_{i}, x,i) \\ & = \sum _{x,y }\hat p(x) p(y \mid x) \sum_{i} s_{l}( y_{i}, x,i) exp(\delta_{k+l} F(x,y)) \\ l &= 1,2,3..K2 \end{aligned} Ep^[sl]l=x,y∑p^(x,y)i∑sl(yi,x,i)=x,y∑p^(x)p(y∣x)i∑sl(yi,x,i)exp(δk+lF(x,y))=1,2,3..K2
F(x,y) 是对数据(x,y)中出现的所有特征数的总和
F ( x , y ) = ∑ k f k ( y , x ) = ∑ k = 1 K ∑ i = 1 n + 1 f k ( y i − 1 , y i , x , i ) F(x,y) = \sum_{k}f_{k}(y,x) = \sum_{k=1}^{K}\sum_{i=1}^{n+1} f_{k}(y_{i-1}, y_{i},x ,i) F(x,y)=∑kfk(y,x)=∑k=1K∑i=1n+1fk(yi−1,yi,x,i)
算法流程
输入:特征函数t1,t2,…tk,s1,s2,…sk,以及经验分布P(X,Y)
输出:参数估计值 w ^ \hat w w^和模型 P w ^ P_{\hat w} Pw^
(1) 初始化
对所有的 k = 1 , 2 , 3 , . . K k = {1,2,3,..K} k=1,2,3,..K, w k = 0 w_{k} = 0 wk=0
(2) 计算 δ k \delta_{k} δk
a.当k = {1,2,3…K1}, δ k \delta_{k} δk是关于特征方程的解
E p ^ [ t k ] = ∑ x , y p ^ ( x ) p ( y ∣ x ) ∑ i t k ( y i − 1 , y i , x , i ) e x p ( δ k F ( x , y ) ) E_{\hat p}[t_{k}] = \sum _{x,y }\hat p(x) p(y \mid x) \sum_{i} t_{k}(y_{i-1}, y_{i}, x,i) exp(\delta_{k} F(x,y)) Ep^[tk]=x,y∑p^(x)p(y∣x)i∑tk(yi−1,yi,x,i)exp(δkF(x,y))
当k = K1+l ,l = {1,2,3…K2}, δ k \delta_{k} δk是关于状态方程的解
E p ^ [ s k ] = ∑ x , y p ^ ( x ) p ( y ∣ x ) ∑ i s l ( y i , x , i ) e x p ( δ k + l F ( x , y ) ) E_{\hat p}[s_{k}] = \sum _{x,y }\hat p(x) p(y \mid x) \sum_{i} s_{l}( y_{i}, x,i) exp(\delta_{k+l} F(x,y)) Ep^[sk]=x,y∑p^(x)p(y∣x)i∑sl(yi,x,i)exp(δk+lF(x,y))
b. 更新权值 w k = w k + δ k w_{k} = w_{k} + \delta_{k} wk=wk+δk
(3) 如果不是所有的w都收敛,重复(2)
拟牛顿算法
没一步一步推导了,下次再看喽。为了说明我看过这方法,还是把图贴这了hhhh

预测问题
CRF的预测问题就是给定CRF模型P(Y|X)以及输入序列x,求出条件概率最大的输出序列 y。也是用Viterbi算法。
从公式上看求解条件概率最大的输出序列 y等价于求解非规范化概率最大的最优路径问题。
y ∗ = a r g m a x y p w ( y ∣ x ) = a r g m a x y e x p ( w ⋅ F ( y , x ) ) Z w ( x ) = a r g m a x y e x p ( w ⋅ F ( y , x ) ) = a r g m a x y ( w ⋅ F ( y , x ) ) \begin{aligned} y^{*} &= argmax_{y} p_{w}(y|x) \\ &= argmax_{y} \frac{exp(w \cdot F(y,x))}{Z_{w}(x)} \\ &= argmax_{y} {exp(w \cdot F(y,x))} \\ &= argmax_{y} (w \cdot F(y,x)) \end{aligned} y∗=argmaxypw(y∣x)=argmaxyZw(x)exp(w⋅F(y,x))=argmaxyexp(w⋅F(y,x))=argmaxy(w⋅F(y,x))
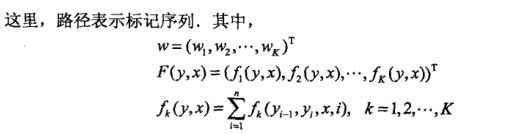
所以求最优路径的问题转化为 m a x y w . F i ( y i − 1 , y i , x ) max_{y} w.F_{i}(y_{i-1},y_{i}, x) maxyw.Fi(yi−1,yi,x)
Viterbi算法
(1) 初始化
标记位置 i= 1时,各个状态(标注)l = 1,2,3…m的概率
δ 1 ( j ) = w . F 0 ( y 0 = s t a r t , y 1 = j , x ) \delta_{1}(j) = w.F_{0}(y_{0} = start, y_{1} = j, x) δ1(j)=w.F0(y0=start,y1=j,x)
(2)递推。求处位置 i的各个标注的非规范化概率的最大值。并记录最大值的路径
δ i ( l ) = m a x 1 < = j < = m δ i − 1 ( j ) + w . F i ( y i − 1 = j , y i = l , x ) l = 1 , 2 , 3... m \delta_{i}(l) = max_{1<=j <=m} \delta_{i-1}(j) + w.F_{i}(y_{i-1} = j, y_{i} = l, x)\quad l =1,2,3...m δi(l)=max1<=j<=mδi−1(j)+w.Fi(yi−1=j,yi=l,x)l=1,2,3...m
记录最大路径
ψ i ( l ) = a r g m a x 1 < = j < = m δ i − 1 ( j ) + w . F i ( y i − 1 = j , y i = l , x ) l = 1 , 2 , 3... m \psi{i}(l) = arg max_{1<=j <=m} \delta_{i-1}(j) + w.F_{i}(y_{i-1} = j, y_{i} = l, x)\quad l =1,2,3...m ψi(l)=argmax1<=j<=mδi−1(j)+w.Fi(yi−1=j,yi=l,x)l=1,2,3...m
(3)终止
直到计算到i=n终止。
此时可以得到非规范化概率的最大值为
m a x y w ⋅ F ( y , x ) = m a x 1 < = j < = m δ n ( j ) max_{y} w \cdot F(y,x) = max_{1<= j <= m} \delta_{n}(j) maxyw⋅F(y,x)=max1<=j<=mδn(j)
最优路径的终点为
y n ∗ = a r g m a x 1 < = j < = m δ n ( j ) y_{n}^{*} = arg max_{1<= j <= m} \delta_{n}(j) yn∗=argmax1<=j<=mδn(j)
回溯求得最优路径
KaTeX parse error: Expected 'EOF', got '\ ' at position 64: …, n-2, ...1 \ \̲ ̲y^{*} = (y^{*}_…


