红黑树教程（动画演示调整过程）--应该是全网最简单易懂的版本
说明
红黑树听起来挺吓人，但当你看完这篇文章后再加上红黑树在线生成练习几次，就能够轻松拿下。
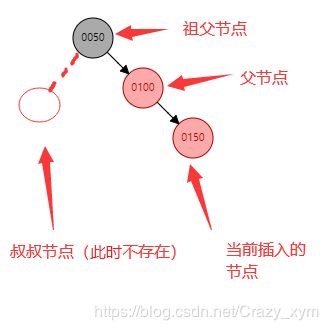
下面的教程中x代表当前插入的节点，xp，xpp，xppl，xppr，uncle，nephewF(far)，nephewC(close)分别为父节点，祖父节点，祖父节点的左孩子，祖父节点的右孩子，叔叔节点，远侄子节点，近侄子节点。
左旋：逆时针旋转
右旋：顺时针旋转
reBalanceAfterInsert()：我们在插入后会调用此方法进行再平衡
reBalanceAfterDelete()：我们在删除节点后会调用此方法进行再平衡
红黑树的约束
1，根节点必须为黑色。
2，红色节点不能有红色节点的孩子
3，从根节点出发到达叶节点所经过的黑色节点个数相同
4，节点必须为红色或黑色
5，一般插入节点为红色
数据结构
class RBTreeNode{
boolean red;
int val;
RBTreeNode left;
RBTreeNode right;
RBTreeNode parent;
}
查找
红黑树本身就是一种二叉查找树，所以可以进行二分查找。这与AVL树或者BST是一致的。
插入
插入时有几种基本情况，更多复杂的情况都可以转换成基本情况求解（重点）。左右都是镜像对称的。这里采用右边插入为例子。
基本情况1
当前树为空，则要插入的节点就是根节点，因此直接插入并将颜色置为黑。
基本情况2
要插入的节点的父节点为黑色，此时直接插入节点。因为增加一个红色节点不会影响当前插入路径上黑色节点个数变化。
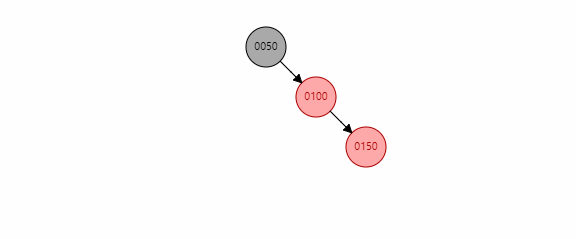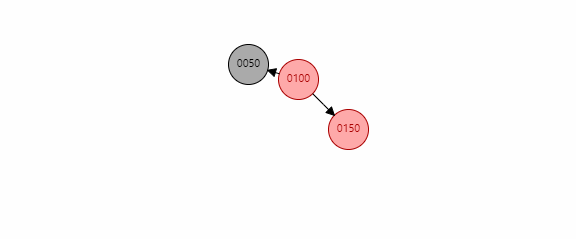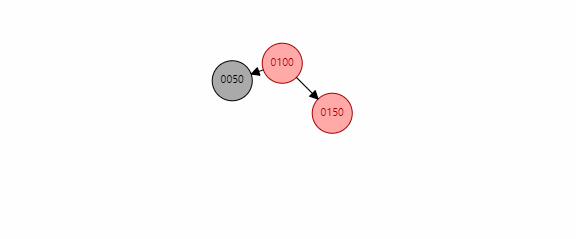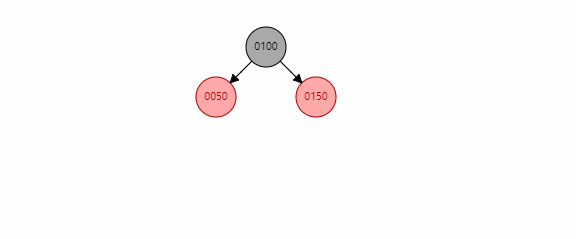
基本情况3（三点一线）
当要插入的节点存在祖父节点，且不存在叔叔节点时，判断x和xp的位置关系，再判断xp和xpp的位置关系。如果是三个节点中一条线上时，称为三点一线。此时我们要做的就是以xp为圆心，xpp进行左旋。在左旋完成后将xp与xpp颜色交换（暴力认为xp置为黑色，xpp置为红色）
if(xp.right == x){
// 再判断xpp
if(xpp.right == xp){
// 此时是图中的情况，这里称为三点一线
}
}
基本情况4(之字形)
这个情况和基本情况3是类似的。只是结构上不再是三点一线而是一种之字形
处理方式是，将x和xp根据位置情况进行旋转，然后转换成情况3。当x是xp的左孩子时，以x为圆心xp进行右旋。然后形成三点一线状态，此时xp位置就是x了，再以x为圆心，xpp进行左旋，变色即可。
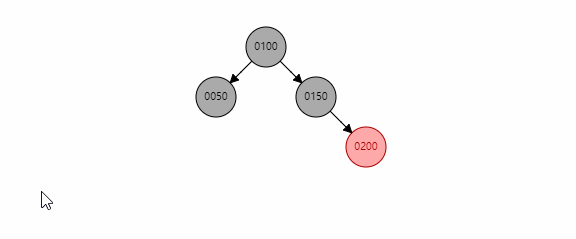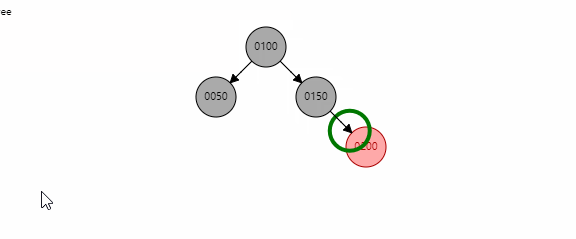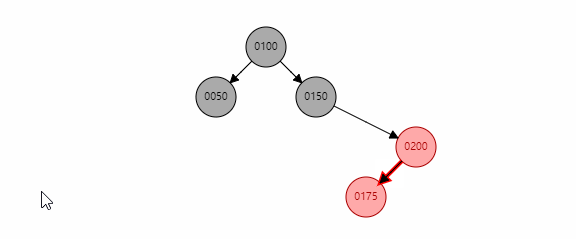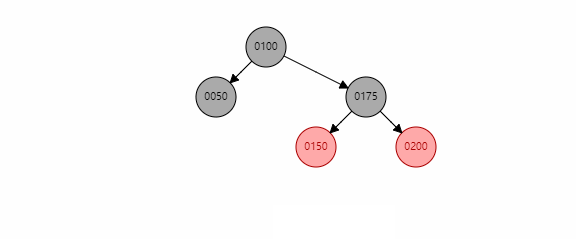
基本情况5
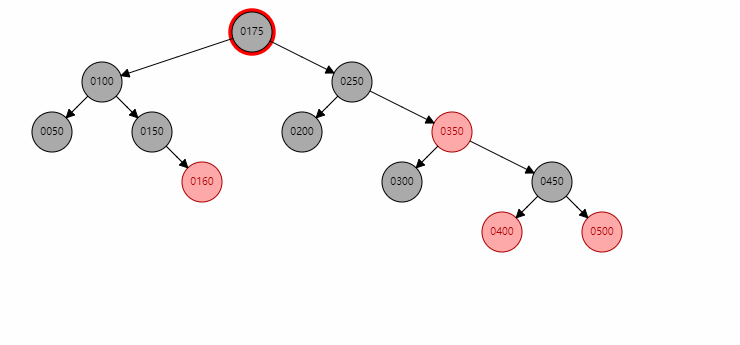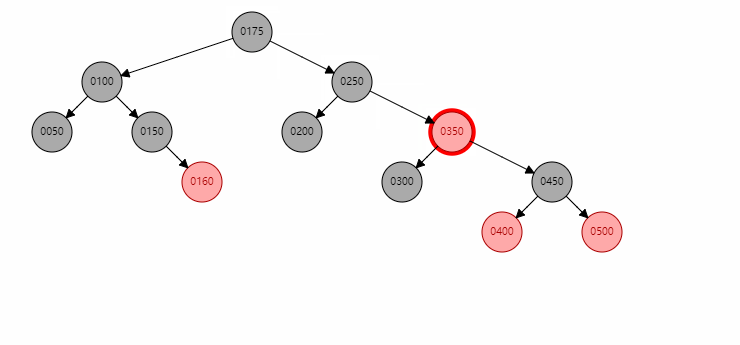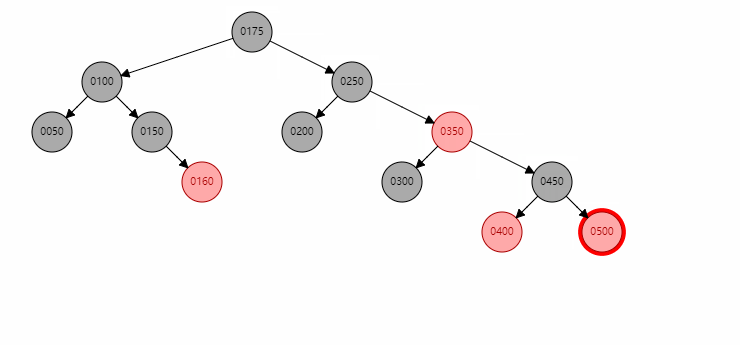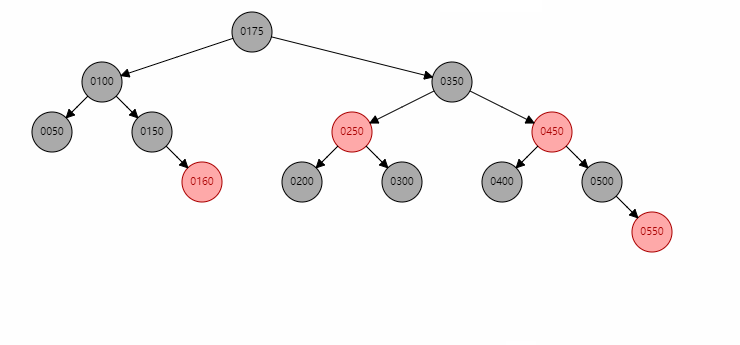
当uncle存在且为红色时，直接将uncle和xp变为黑色，xpp变为红色，同时再调用reBalanceAfterInsert()判断对剩余树颜色的影响。从图中看到，在xpp变为红色后会进行reBalanceAfterInsert()将根节点xpp染成黑色。
基本情况6
当uncle存在且为黑色时，只需要以xp为圆心xpp进行旋转并将uncle置为红色即可。图中是先进行了情况5的调整，然后再进行情况6的调整。
删除
对于删除来说需要考虑的比插入多一点情况，但是也不难。
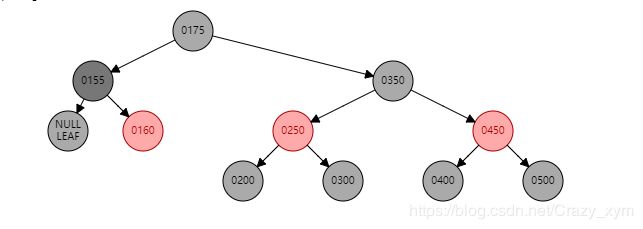
首先看下整颗红黑树形态
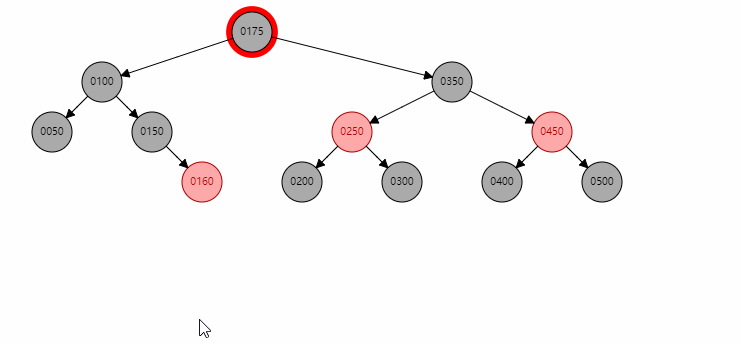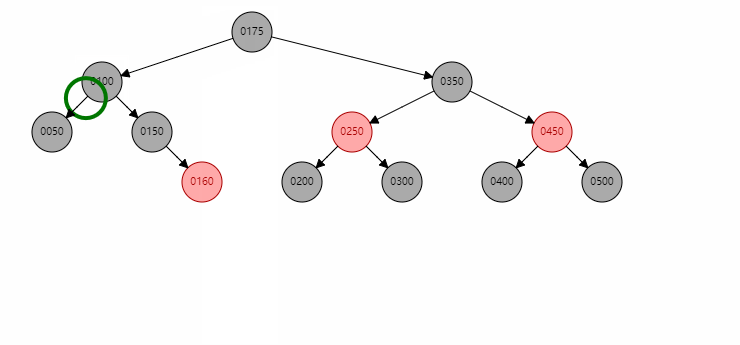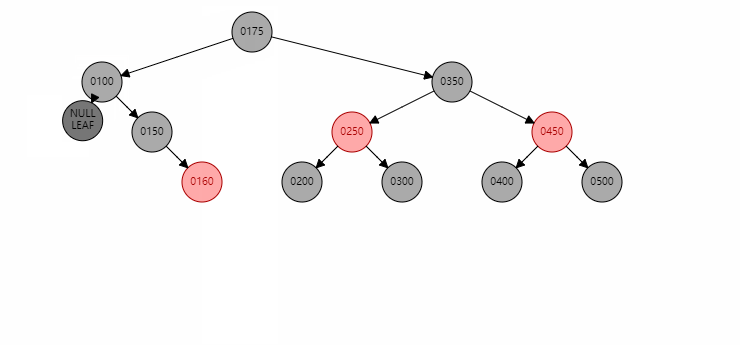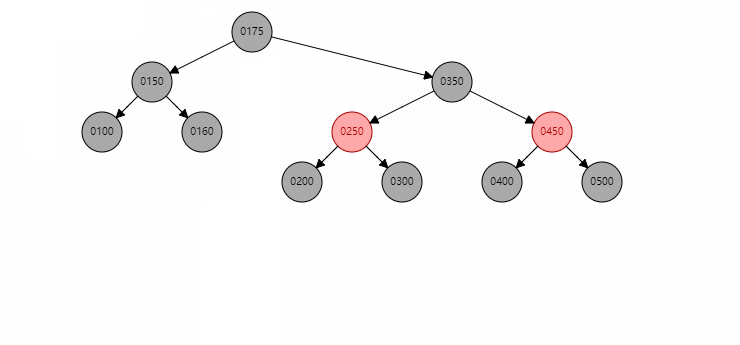
基本情况1
删除的节点为红色节点，直接删除即可，比如删除550。
基本情况2
删除的节点为黑色，且无左右子节点。比如删除50。此时需要判断nephewF也就是远侄子节点是否存在，对于上图50的nephewF节点为160。此时远侄子节点存在且为红色，那么需要以兄弟节点 150为圆心，xp 100绕其进行左旋。然后将100和160染成黑色。
基本情况3
远侄子不存在，但是近侄子存在且为黑色。这里处理方式和插入时情况4转成情况3是一样的。以近侄子为圆心，兄弟节点绕其旋转，变成远侄子的情况，再使用情况2进行处理。
基本情况4
当出现当前节点无孩子，且存在兄弟节点也无孩子，且父节点为黑色时。
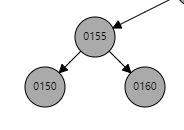
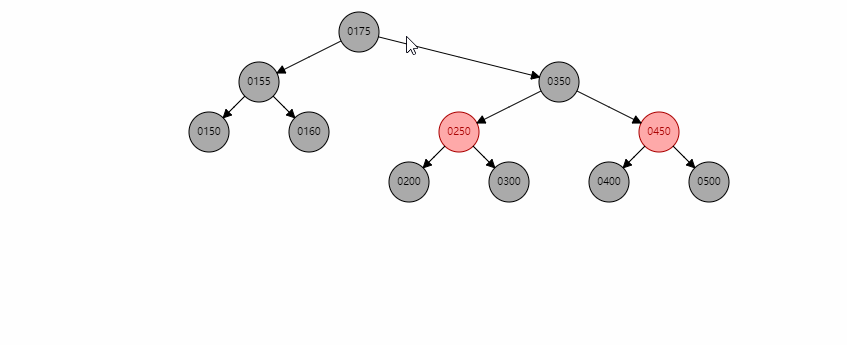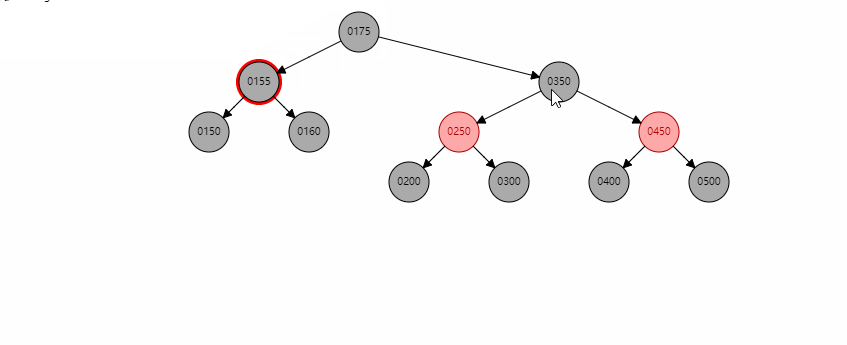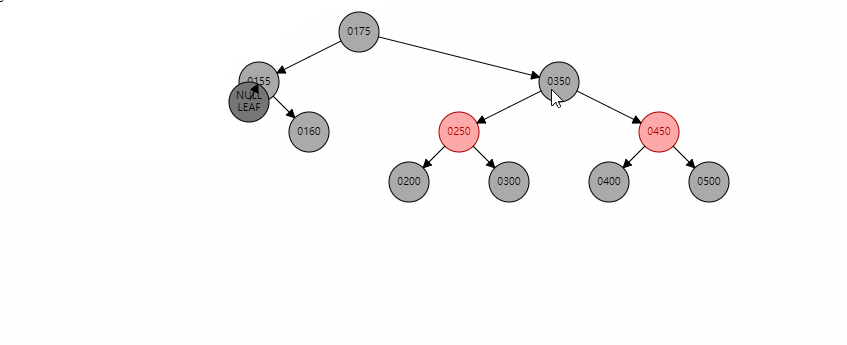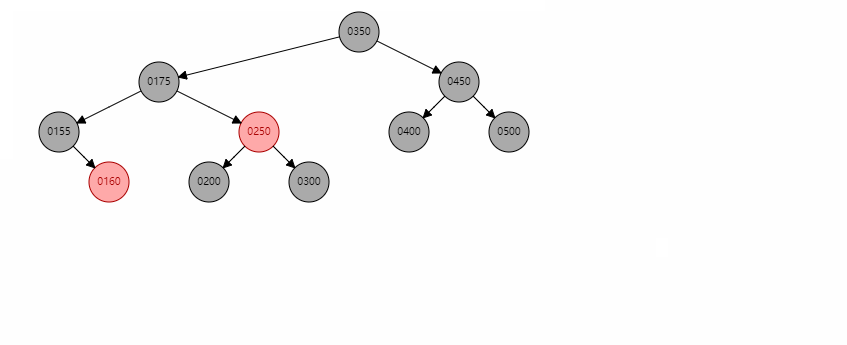
此时假如要删除150，在删除后，左子树路径黑色节点个数少一个，因此需要将右边路径也-1，那么最快的方法就是将160设置为红色，那么此时对于更大一层的树而言，155节点那条路上也少了一个黑色节点，则需要再一次调用reBalanceAfterDelete()。可以明显的看出以155为调整的节点来说，存在远侄子节点450，那么就转换成情况2。则接下来会以350为圆心，175绕其进行左旋，然后将250置为175的右孩子，350变成根节点，然后450被染成黑色。调整结束。
基本情况5
当存在兄弟节点并且父节点为红色时。如图
此时假设删除200，那么删除后左边路径黑色节点个数少一个，应该将右边节点个数也-1，那么就将300置为红色，然后250置为黑色。调整结束。可以发现在经过上面方法调整后，并没有对更大层面产生影响。
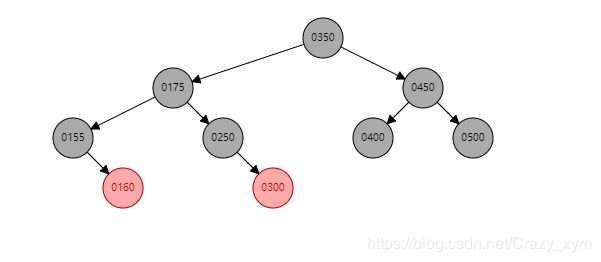
基本情况6
当节点只有一个孩子且为红色时，直接将xp指向child，同时child颜色变成黑色。以删除155为例。
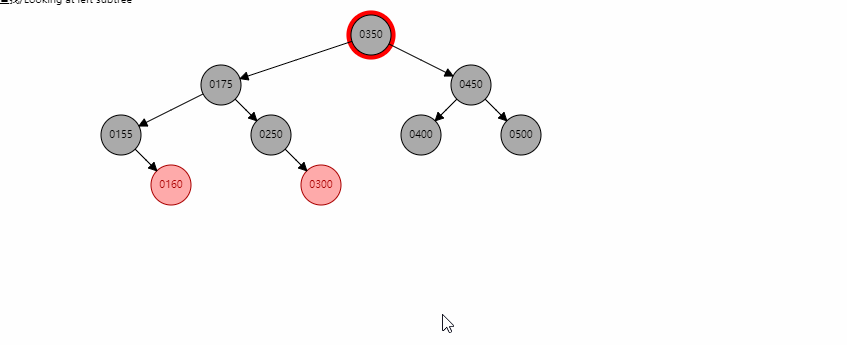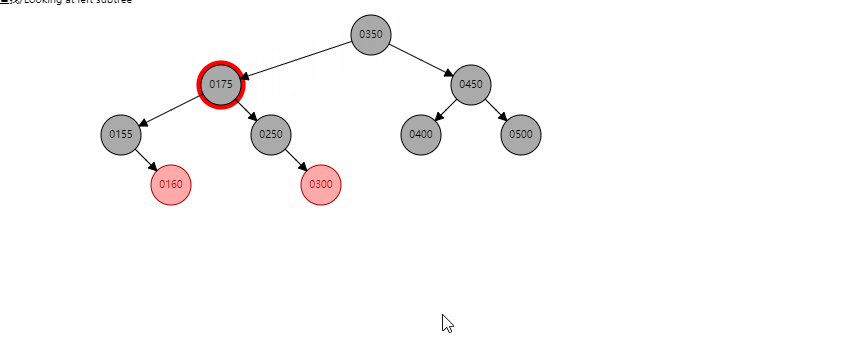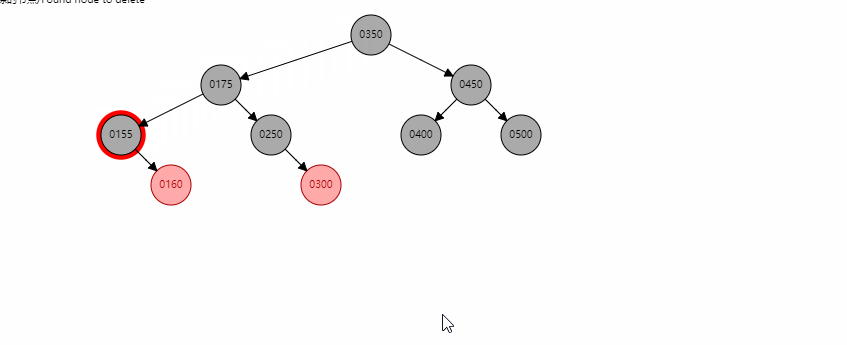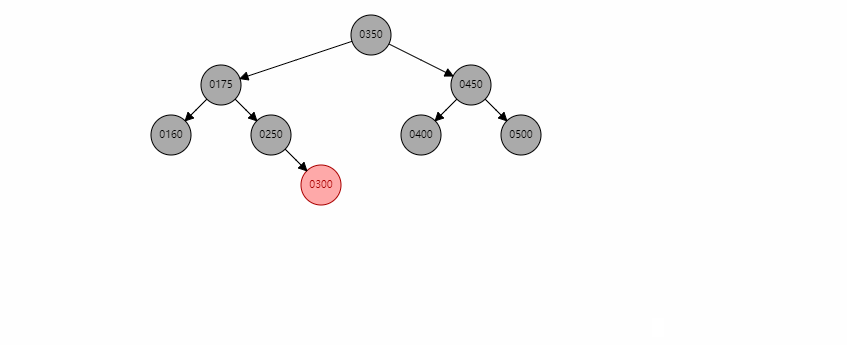
基本情况7
当存在左右孩子时，找到左子树中最大的节点C，将其值赋给x，然后转换成对C的删除操作。
这里以删除350为例，首先找到300，然后将300的值赋给350节点，然后变成对300这个红色节点的删除。
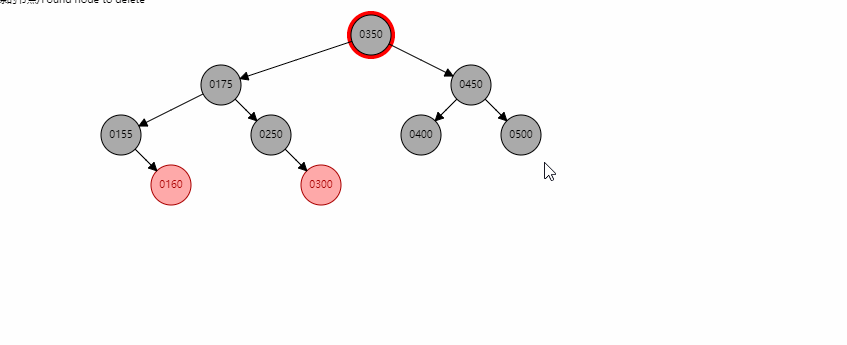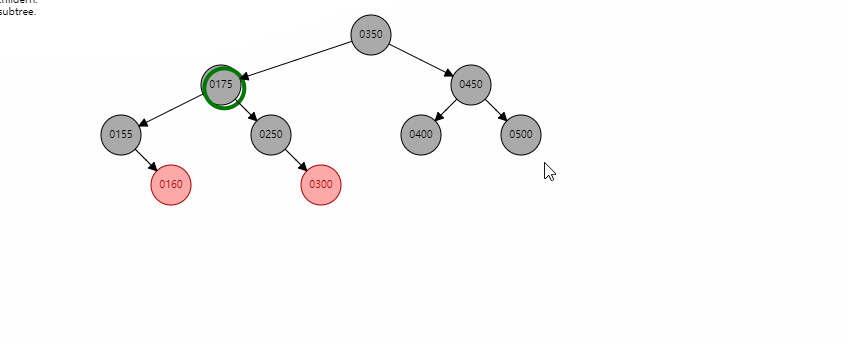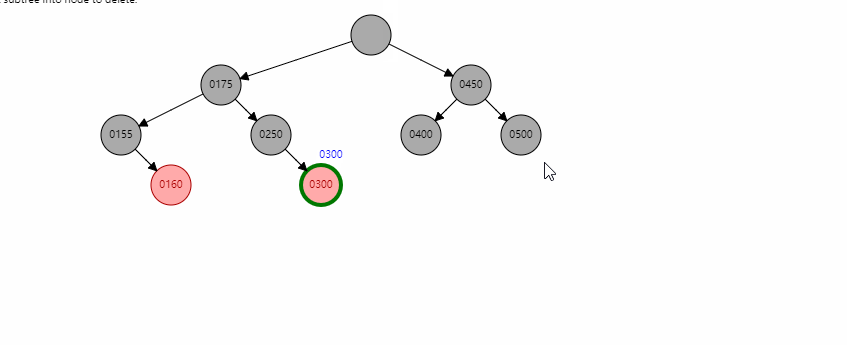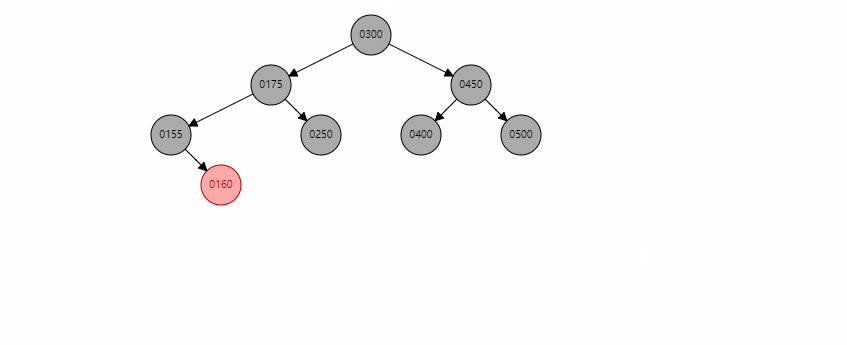
可能这个例子太简单了，这边还有一个例子供大家学习。
首先找到左子树最大节点250，然后将250的值赋给300，再变成对250的删除，此时发现存在近侄子情况，因此是情况3。将以近侄子160为圆心，155绕其进行一次左旋，随后变成情况2，再将175以160为圆心进行右旋，调整结束。
