智慧魔珠金字塔(类似俄罗斯方块)的所有情况 python
一. 首先呢,我们介绍一下这东西:
名称: 智慧魔珠金字塔
规则:应该有些人玩过了
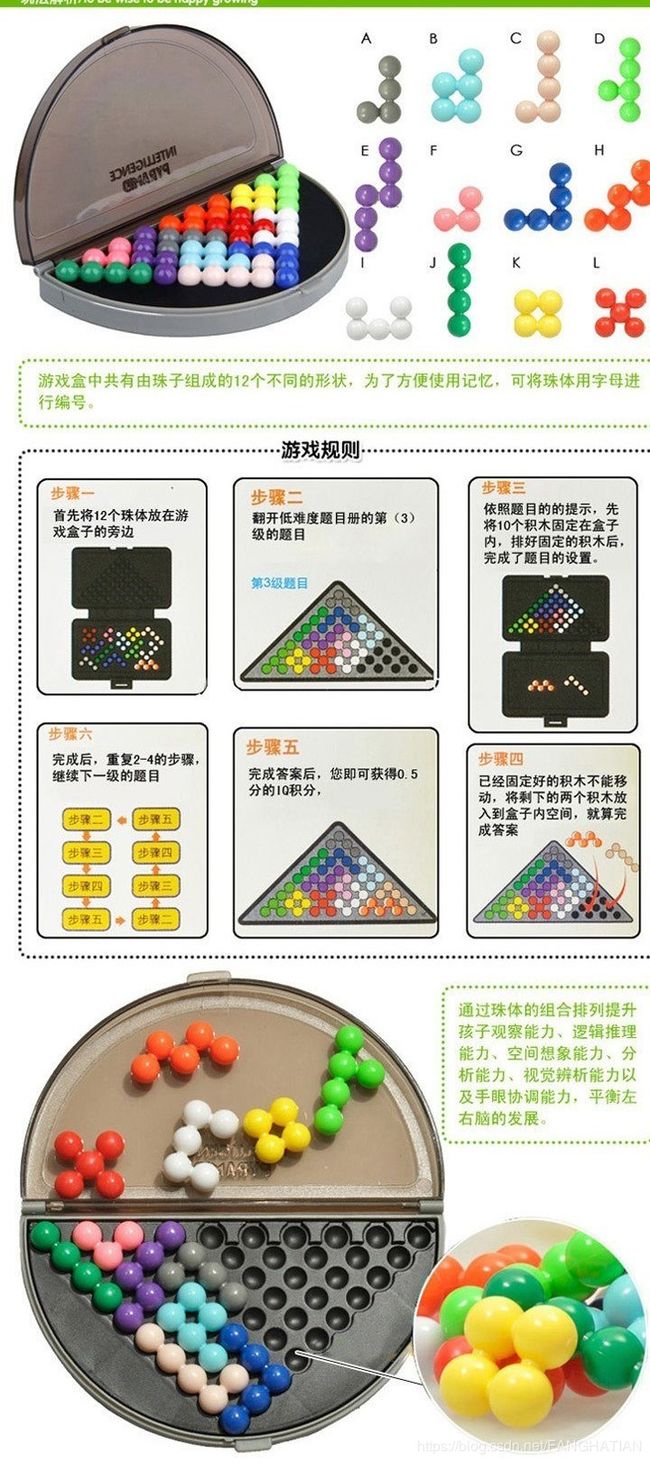
二. python实现:
说一下主要的算法,我们先初始化一个chessboard(类似一个等腰直角三角形):
chessboard = [[0]*i for i in range(10, 0, -1)]
然后再模拟棋子——通过打表,这里我们把棋子放进一个矩形里,以左下角为基准,算出每个点的相对位置
如A号棋子(见上方)的一种情况我们可以表示为[[0,0],[0,1],[1,1],[2,1]](第一个为行,第二个为列)
通过计算共有60种情况(包括旋转,对称),12颗棋子
然后进行枚举对左下角的那个点进行枚举,并判断是否能放(这里可能会超出列表范围),如果可以,则枚举下一刻;如果不行则继续枚举这颗;直至12颗棋子枚举完
下面附上代码:
from time import time
def dfs(n_1):
global ans, chessboard, time_start
flag, a, u_2, u_1 = True, [] ,0 ,0
for i in range(9,-1,-1):#每行的个数
for j in range(i):#每一行挨个逐次搜索
for s in range(len(biao[n_1])):#旋转对称
if pd(9-i,j,n_1,s):
flag,u_1 = False,u_1+1
if n_1 < 11:
if dfs(n_1+1):
for o in range(len(biao[n_1][s])):
chessboard[9-i + biao[n_1][s][o][0]][j + biao[n_1][s][o][1]] = 0
u_2 += 1
else:
time_end = time()
ans += 1
print('第'+str(time_end-time_start)+'秒算出:'+'第'+str(ans)+'个答案如下:')
for a in range(10):
print(chessboard[a])
for o in range(len(biao[n_1][s])):
chessboard[9 - i + biao[n_1][s][o][0]][j + biao[n_1][s][o][1]] = 0
return True
if u_1 == u_2:
return True
if flag:
return True
def jianzhi():
for i in range(9,-1,-1):
for j in range(i):
if chessboard[9-i][j] == 0:
h = 1
for o in range(4):
i_1,j_1 = 9-i,j
while 0<=i_1+go[o][0]<=9-j_1 and 0<=j_1+go[o][1]<=9-i_1:
i_1,j_1=i_1+go[o][0],j_1+go[o][1]
if chessboard[i_1][j_1] == 0:
h += 1
else:
break
if h<3:
return False
return True
def pd(x, y, i, j):
for s in range(len(biao[i][j])):
if x + biao[i][j][s][0] <= chessboardgeshu[y + biao[i][j][s][1]] and\
y + biao[i][j][s][1] <= chessboardgeshu[x + biao[i][j][s][0]]:
if chessboard[x + biao[i][j][s][0]][y + biao[i][j][s][1]] != 0:
return False
else:
return False
for s in range(len(biao[i][j])):
chessboard[x + biao[i][j][s][0]][y + biao[i][j][s][1]] = i + 1
if jianzhi():
return True
else:
for s in range(len(biao[i][j])):
chessboard[x + biao[i][j][s][0]][y + biao[i][j][s][1]] = 0
return False
if __name__ == '__main__':
time_start = time()
j, i, a, h, chessboard, ans = 0, 0, [], 0, [], 0
go = [[0,1],[1,0],[0,-1],[-1,0]]
for i in range(10,0,-1):
for j in range(i):
a.append(0)
chessboard.append(a)
a = []#初始化表格
for i in range(10):
print(chessboard[i])
chessboardgeshu = [9, 8, 7, 6, 5, 4, 3, 2, 1, 0, -1, -1, -1, -1]
biao =[[[[0, 1], [1, 0], [1, 1], [2, 0], [2, 1]],
[[0, 0], [0, 1], [1, 0], [1, 1], [2, 1]],
[[0, 0], [0, 1], [1, 0], [1, 1], [2, 0]],
[[0, 0], [1, 0], [1, 1], [2, 0], [2, 1]],
[[0, 0], [0, 1], [1, 1], [0, 2], [1, 2]],
[[1, 0], [0, 1], [1, 1], [0, 2], [1, 2]],
[[0, 0], [1, 0], [0, 1], [1, 1], [0, 2]],
[[0, 0], [1, 0], [0, 1], [1, 1], [1, 2]]],
[[[2, 0], [2, 1], [1, 1], [1, 2], [0, 2]],
[[0, 0], [1, 0], [1, 1], [2, 1], [2, 2]],
[[0, 0], [0, 1], [1, 1], [1, 2], [2, 2]],
[[2, 0], [1, 0], [1, 1], [0, 1], [0, 2]]],
[[[0, 0], [1, 0], [0, 1], [0, 2], [1, 2]],
[[0, 0], [1, 0], [1, 1], [1, 2], [0, 2]],
[[0, 0], [1, 0], [2, 0], [2, 1], [0, 1]],
[[0, 0], [0, 1], [1, 1], [2, 1], [2, 0]]],
[[[1, 0], [1, 1], [0, 1], [1, 2], [2, 1]]],
[[[0, 1], [1, 1], [2, 1], [3, 1], [3, 0]],
[[0, 0], [1, 0], [2, 0], [3, 0], [3, 1]],
[[0, 0], [0, 1], [1, 0], [2, 0], [3, 0]],
[[0, 0], [0, 1], [1, 1], [2, 1], [3, 1]],
[[0, 0], [1, 0], [0, 1], [0, 2], [0, 3]],
[[0, 0], [1, 0], [1, 1], [1, 2], [1, 3]],
[[0, 0], [1, 3], [0, 1], [0, 2], [0, 3]],
[[0, 3], [1, 0], [1, 1], [1, 2], [1, 3]]],
[[[0, 0], [1, 0], [1, 1], [0, 1]]],
[[[0, 0], [1, 0], [2, 0], [3, 0]],
[[0, 0], [0, 1], [0, 2], [0, 3]]],
[[[0, 0], [1, 0], [2, 0], [3, 0], [2, 1]],
[[0, 0], [1, 0], [2, 0], [3, 0], [1, 1]],
[[0, 1], [1, 1], [2, 0], [2, 1], [3, 1]],
[[0, 1], [1, 1], [1, 0], [2, 1], [3, 1]],
[[0, 0], [0, 1], [0, 2], [0, 3], [1, 1]],
[[0, 0], [0, 1], [0, 2], [0, 3], [1, 2]],
[[1, 0], [1, 1], [1, 2], [1, 3], [0, 1]],
[[1, 0], [1, 1], [1, 2], [1, 3], [0, 2]]],
[[[0, 1], [1, 1], [2, 1], [2, 0]],
[[0, 1], [1, 1], [2, 1], [0, 0]],
[[0, 0], [1, 0], [2, 0], [2, 1]],
[[0, 0], [1, 0], [2, 0], [0, 1]],
[[0, 0], [0, 1], [0, 2], [1, 2]],
[[0, 0], [0, 1], [0, 2], [1, 0]],
[[1, 0], [1, 1], [1, 2], [0, 0]],
[[1, 0], [1, 1], [1, 2], [0, 2]]],
[[[2, 0], [2, 1], [2, 2], [1, 2], [0, 2]],
[[0, 0], [1, 0], [2, 0], [2, 1], [2, 2]],
[[0, 0], [1, 0], [2, 0], [0, 1], [0, 2]],
[[0, 0], [0, 1], [0, 2], [1, 2], [2, 2]]],
[[[1, 0], [1, 1], [0, 1], [0, 2], [0, 3]],
[[0, 0], [0, 1], [1, 1], [1, 2], [1, 3]],
[[1, 0], [1, 1], [1, 2], [0, 2], [0, 3]],
[[0, 0], [0, 1], [0, 2], [1, 2], [1, 3]],
[[3, 0], [2, 0], [1, 0], [1, 1], [0, 1]],
[[0, 0], [1, 0], [2, 0], [2, 1], [3, 1]],
[[0, 0], [1, 0], [1, 1], [2, 1], [3, 1]],
[[3, 0], [2, 0], [2, 1], [1, 1], [0, 1]]],
[[[1, 0], [0, 0], [0, 1]],
[[0, 0], [0, 1], [1, 1]],
[[0, 0], [1, 1], [1, 0]],
[[0, 1], [1, 1], [1, 0]]]]#初始化每个棋子的形状
dfs(0)#进行深搜
print(ans,'完成')
如有大佬有更好的算法可以在评论区写