推荐系统算法（MF、FM、CF、SVD、LFM、SVD++、TItemCF、timeSVD++、模型融合）

为什么需要矩阵分解？(matrix factorization model)

协同过滤可以解决我们关注的很多问题，但是仍然有一些问题存在，比如：

• 物品之间存在相关性，信息量并不随着向量维度增加而线性增加
• 矩阵元素稀疏，计算结果不稳定，增减一个向量维度，导致近邻结果差异很大的情况存在

上述两个问题，在矩阵分解中可以得到解决。原始的矩阵分解只适用于评分预测问题，这里所讨论的也只是针对于评分预测问题。常用的分解算法有SVD和SVD++。

矩阵分解（MF）

目前推荐系统中用的最多的就是矩阵分解方法，在Netflix Prize推荐系统大赛中取得突出效果。以用户-项目评分矩阵为例，矩阵分解就是预测出评分矩阵中的缺失值，然后根据预测值以某种方式向用户推荐。常见的矩阵分解方法有

• 基本矩阵分解（basic MF）
• 正则化矩阵分解（Regularized MF）
• 基于概率的矩阵分解（PMF）
• 非负矩阵（Non-negative MF
• 正交非负矩阵（Orthogonal non-negative MF）
• pca 与 svd的关系： pca是一种手段，svd是pca求解的方法，svd处理非方阵，当然我们可以通过特征值分解来做pca
• 简单来说，就是把原来的大矩阵，近似分解成两个小矩阵的乘积，在实际推荐计算时不再使用大矩阵，而是使用分解得到的两个小矩阵。
• 具体来说，假设用户物品评分矩阵为 R，形状为 mxn，即 m 个用户， n 个物品。我们选择一个很小的数 k，k 比 m 和 n
  都小很多，然后通过算法生成两个矩阵 P 和 Q，这两个矩阵的要求如下：P 的形状是 mxk，Q 的形状是 nxk， P 和 Q
  的转置相乘结果为 R。也就是说分解得到的矩阵P和Q可以还原成原始的矩阵R。

用公式来描述就是：

其中 R 表示真实的用户评分矩阵，一般有很多缺失值（缺失值表示用户没有对该物品评分），带尖帽的 R 表示使用分解矩阵预测的用户评分矩阵，它补全了所有的缺失值。

另一个角度

矩阵分解就是把用户和物品都映射到一个 k 维空间中（这里映射后的结果用户用矩阵P表示，物品用矩阵Q表示），这个 k 维空间不是我们直接看得到的，也不一定具有非常好的可解释性，每一个维度也没有名字，所以常常叫做隐因子。用户向量代表了用户的兴趣，物品向量代表了物品的特点，且每一个维度相互对应，两个向量的内积表示用户对该物品的喜好程度。

因子分解机算法Factorization Machines（FM）

请查看我的另一篇博客

协同过滤算法collaborative filtering（CF）

请查看我的另一篇博客

1.传统的SVD分解

对于如何补全一个矩阵，历史上有过很多的研究。一个空的矩阵有很多种补全方法，而我们要找的是一种对矩阵扰动最小的补全方法。那么什么才算是对矩阵扰动最小呢？一般认为，如果补全后矩阵的特征值和补全之前矩阵的特征值相差不大，就算是扰动比较小。所以，最早的矩阵分解模型就是从数学上的SVD（奇异值分解）开始的。给定m个用户和n个物品，和用户对物品

奇异值分解将矩阵分解为奇异值和奇异向量

R是一个mn的矩阵，U是一个mm的矩阵，S是一个mn的矩阵，V是一个nn的矩阵

矩阵S对角元素上的值称为矩阵A的奇异值，U的列向量称为左奇异向量，V的列向量称为右奇异向量

左奇异向量是RRT的特征向量，右奇异向量是RTR的特征向量，A的非零奇异值是和特征值的平方根

SVD分解是早期推荐系统研究常用的矩阵分解方法，不过该方法具有以下缺点，因此很难在实际系统中应用。

• 该方法首先需要用一个简单的方法补全稀疏评分矩阵。一般来说，推荐系统中的评分矩阵是非常稀疏的，一般都有95%以上的元素是缺失的。而一旦补全，评分矩阵就会变成一个稠密矩阵，从而使评分矩阵的存储需要非常大的空间，这种空间的需求在实际系统中是不可能接受的。
• 该方法依赖的SVD分解方法的计算复杂度很高，特别是在稠密的大规模矩阵上更是非常慢。一般来说，这里的SVD分解用于1000维以上的矩阵就已经非常慢了，而实际系统动辄是上千万的用户和几百万的物品，所以这一方法无法使用。如果仔细研究关于这一方法的论文可以发现，实验都是在几百个用户、几百个物品的数据集上进行的。

想具体了解推荐系统中常用的LFM算法，可以参考我的另一篇博客

LFM提出之后获得了很大的成功，后来很多著名的模型都是通过对LFM修修补补获得的，下面的各节将分别介绍一下改进LFM的各种方法。这些改进有些是对模型的改进，有些是将新的数据引入到模型当中。

4.考虑邻域影响的LFM（SVD++）

前面的LFM模型中并没有显式地考虑用户的历史行为对用户评分预测的影响。为此，Koren在Netflix Prize比赛中提出了一个模型，将用户历史评分的物品加入到了LFM模型中，Koren将该模型称为SVD++。
在介绍SVD++之前，我们首先讨论一下如何将基于邻域的方法也像LFM那样设计成一个可以学习的模型。其实很简单，我们可以将ItemCF的预测算法改成如下方式：


可以看到评分函数加了用户对有过评分商品的行为隐式yj反馈之后，式子变得复杂了一些，但是改变的也不是太多，因此 SVD++ 的代码就是从SVD的代码修改而来。主要改了预测函数p（Ui，Mj），增加了用户对商品的隐式反馈向量的计算，训练，更新；以及用户对商品的行为集合构建。

5.加入时间信息(1.TItemCF、2.timeSVD++)

无论是MovieLens数据集还是Netflix Prize数据集都包含时间信息，对于用户每次的评分行为，都给出了行为发生的时间。因此，在Netflix Prize比赛期间，很多研究人员提出了利用时间信息降低预测误差的方法。
利用时间信息的方法也主要分成两种，一种是将时间信息应用到基于邻域的模型中，另一种是将时间信息应用到矩阵分解模型中。下面将分别介绍这两种算法。

6.模型融合

Netflix Prize的相关实验结果

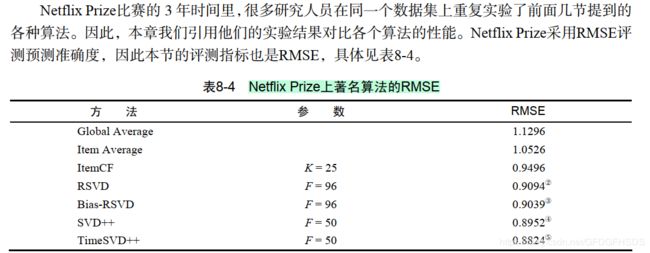
可以看到，改进后的TimesSVD++ 均方根误差最低为0.8824，性能最优！

附Python实现SVD++代码

class SVDPP(object):
    """
    implementation of SVD++ for CF
    """
    def __init__(self, epoch, eta, userNums, itemNums, ku=0.001, km=0.001, \
                f=30,save_model=False):
        super(SVDPP, self).__init__()
        self.epoch = epoch
        self.userNums = userNums
        self.itemNums = itemNums
        self.eta = eta
        self.ku = ku
        self.km = km
        self.f = f
        self.save_model = save_model

        self.U = None
        self.M = None


    def fit(self, train, val=None):
        # 构造每个用户有过评分的行为字典
        self.Udict = {}
        for i in range(train.shape[0]):
            uid = train[i,0]
            iid = train[i,1]
            self.Udict.setdefault(uid,[])
            self.Udict[uid].append(iid)

        rateNums = train.shape[0]
        self.meanV = np.sum(train[:,2]) / rateNums
        initv = np.sqrt((self.meanV - 1) / self.f)
        self.U = initv + np.random.uniform(-0.01,0.01,(self.userNums+1,self.f))
        self.M = initv + np.random.uniform(-0.01,0.01,(self.itemNums+1,self.f))
        self.bu = np.zeros(self.userNums + 1)
        self.bi = np.zeros(self.itemNums + 1)
        self.y = np.zeros((self.itemNums+1, self.f)) + 0.1
        
        start = time.time()
        for i in range(self.epoch):
            sumRmse = 0.0
            for sample in train:
                uid = sample[0]
                iid = sample[1]
                vij = float(sample[2])

                sumYj, sqrt_Ni = self.get_Yi(uid)
                # p(U_i,M_j) = \mu + b_i + b_u + U_i^T (M_j + \frac{1}{\sqrt{|N_i|^2}}*\sum_{j\in N_i}y_j)
                p = self.meanV + self.bu[uid] + self.bi[iid] + \
                    np.sum(self.M[iid] * (self.U[uid] + sumYj))

                error = vij - p
                sumRmse += error**2
                # 计算Ui,Mj的梯度
                deltaU = error * self.M[iid] - self.ku * self.U[uid]
                deltaM = error * (self.U[uid] + sumYj) - self.km * self.M[iid]
                # 更新参数
                self.U[uid] += self.eta *  deltaU
                self.M[iid] += self.eta *  deltaM

                self.bu[uid] += self.eta * (error - self.ku * self.bu[uid])
                self.bi[iid] += self.eta * (error - self.km * self.bi[iid])

                # for j in self.Udict[uid]:
                #     self.y[j] += self.eta * (error * self.M[j]/sqrt_Ni - self.ku * self.y[j])

                rating_list = self.Udict[uid]
                self.y[rating_list] += self.eta * (error * self.M[rating_list]/sqrt_Ni - \
                    self.ku * self.y[rating_list])

            trainRmse = np.sqrt(sumRmse/rateNums)

            if val.any():
                _ , valRmse = self.evaluate(val)
                print("Epoch %d cost time %.4f, train RMSE: %.4f, validation RMSE: %.4f" % \
                    (i, time.time()-start, trainRmse, valRmse))
            else:
                print("Epoch %d cost time %.4f, train RMSE: %.4f" % \
                    (i, time.time()-start, trainRmse))

        if self.save_model:
            model = (self.meanV, self.bu, self.bi, self.U, self.M)
            pickle.dump(model, open(save_model + '/svcRecModel.pkl', 'wb'))


    def evaluate(self, val):
        loss = 0
        pred = []
        for sample in val:
            uid = sample[0]
            iid = sample[1]
            if uid > self.userNums or iid > self.itemNums:
                continue
            sumYj, _ = self.get_Yi(uid)
            predi = self.meanV + self.bu[uid] + self.bi[iid] \
                    + np.sum(self.M[iid] * (self.U[uid] + sumYj))
            if predi < 1:
                predi = 1
            elif predi > 5:
                predi = 5
            pred.append(predi)

            if val.shape[1] == 3:
                vij = sample[2]
                loss += (predi - vij)**2

        if val.shape[1] == 3:
            rmse = np.sqrt(loss/val.shape[0])
            return pred, rmse

        return pred

    def predict(self,test):

        return self.evaluate(test)

    # 计算 sqrt_Ni 和 ∑yj
    def get_Yi(self,uid):
        Ni = self.Udict[uid]
        numNi = len(Ni)
        sqrt_Ni = np.sqrt(numNi)
        yj = np.zeros((1, self.f))
        if numNi == 0:
            sumYj = yj + 0.1
        else:
            yj = np.mean(self.y[Ni],axis=0)
            sumYj = yj / sqrt_Ni
        return sumYj, sqrt_Ni

参考

[1]：项亮《推荐系统实战》