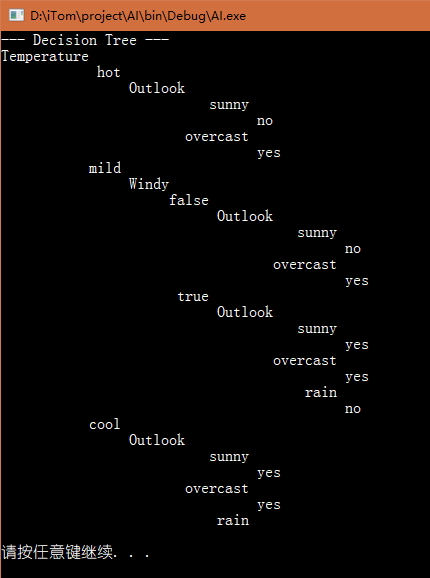
C++ 实现决策树 ID3 算法

Reference

一步一步详解ID3和C4.5的C++实现
决策树之ID3算法

Notes

• ID3只能处理离散性的属性，属性的每一种取值就刚好对应于树上结点的一个分枝；
• 样本空间是字符串形式的，为了处理方便，对每个属性（包括 label）分别将它们的各种取值都映射为一个整数（离散化，数字化），主要是我是用vector套vector的方式存样本空间，这样属性的取值又刚好与下标对应；
• 也是为了方便，程序要求先输入样本个数、属性个数，还有每个属性的名字，在输出决策树时用；

Rendering

• 输入样本空间

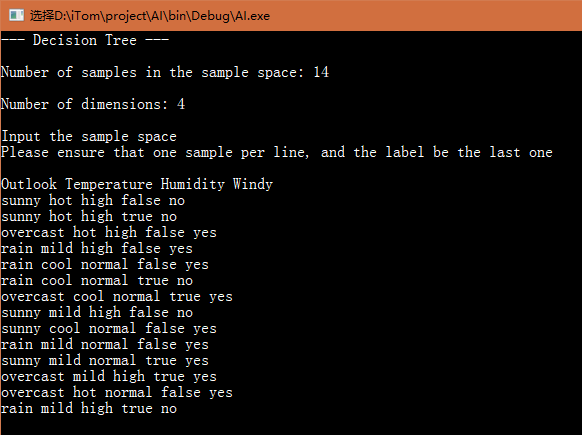
其中，样本空间上面的那一行是属性名字，但没有 label 的名字

• 打印决策树

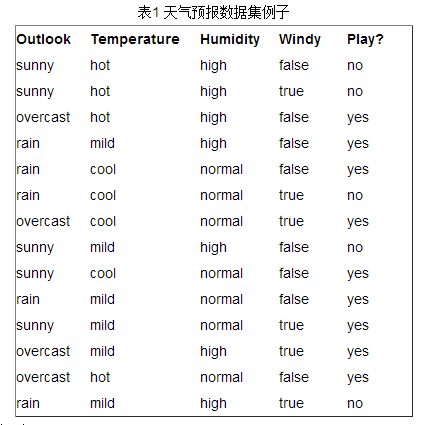
Sample Space

输入的文本如下：

14 4
Outlook Temperature Humidity Windy
sunny hot high false no
sunny hot high true no
overcast hot high false yes
rain mild high false yes
rain cool normal false yes
rain cool normal true no
overcast cool normal true yes
sunny mild high false no
sunny cool normal false yes
rain mild normal false yes
sunny mild normal true yes
overcast mild high true yes
overcast hot normal false yes
rain mild high true no

Code

决策树结点

struct dtNode
{
    int n_child;
    int attr_id;
    int label;
    vector child;

    dtNode(): n_child(0), attr_id(-1), label(-1) {}
    ~dtNode() { child.clear(); }
};

决策树类

typedef vector<vector<int> > SampleSpace;

class DecisionTree
{
    int n_dim;
    int n_sample;
    vector<string> attribute;
    SampleSpace samspc;
    vector<map<string,int> > dsc;
    vector<map<int,string> > rev;
    dtNode *root;

private:
    void _formatting(const vector<vector<string> > &in_sample_space);
    void _build(SampleSpace, dtNode *&);
    bool _same_class(const SampleSpace &);
    int _most_label(const SampleSpace &);
    int _max_gain_attr(const SampleSpace &);
    double _info_gain(const SampleSpace &, int attr);
    SampleSpace _drop_attr(SampleSpace, int attr);
    void _clear(dtNode *&);
    void _print_tree(dtNode *, int indent);

public:
    DecisionTree(int n_dimension, int n_sample);
    ~DecisionTree();
    void input();
    void build();
    void display();
};

完整代码

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

using std::cin;
using std::cout;
using std::endl;
using std::map;
using std::setw;
using std::string;
using std::vector;

/*------- 决策树结点 -------*/

struct dtNode
{
    int n_child; // 子结点个数
    int attr_id; // 按哪个属性来分类
    int label; // 分类标签
    vector child; // 子结点指针

    dtNode(): n_child(0), attr_id(-1), label(-1) {}
    ~dtNode() { child.clear(); }
};

/*------- 决策树 -------*/

typedef vector<vector<int> > SampleSpace;

class DecisionTree
{
    // 样本的维数（属性数）
    int n_dim;
    // 样本个数
    int n_sample;
    // 各属性的名字 -> 用来打印
    vector<string> attribute;
    // 样本空间
    SampleSpace samspc;
    // 离散化，把每一个属性（包括标签）的所有取值（字符串）都离散化成数字
    vector<map<string,int> > dsc;
    // 反离散化，根据离散化后的数字找回离散化前的字符串 -> 用来打印
    vector<map<int,string> > rev;
    // 决策树树根
    dtNode *root;

private:
    // 离散化，将输入的字符串形式的样本空间转化成数字形式的样本空间
    void _formatting(const vector<vector<string> > &in_sample_space);
    // 建树
    void _build(SampleSpace, dtNode *&);
    // 判断传入的样本空间是否所有样本的 label 都一样
    bool _same_class(const SampleSpace &);
    // 找到传入的样本空间里占最多数的 label
    int _most_label(const SampleSpace &);
    // 找到能获得最大信息增益的（还没被删的）分类属性
    int _max_gain_attr(const SampleSpace &);
    // 按某个属性来算信息增益
    double _info_gain(const SampleSpace &, int attr);
    // 删掉样本空间的某个属性（把那一列标为负数）
    SampleSpace _drop_attr(SampleSpace, int attr);
    // 砍树
    void _clear(dtNode *&);
    // 打印决策树
    void _print_tree(dtNode *, int indent);

public:
    // constructor
    DecisionTree(int n_dimension, int n_sample);
    // destructor
    ~DecisionTree();
    // 输入样本空间（字符串形式）
    void input();
    // 建树（驱动函数）
    void build();
    // 打印决策树（驱动函数）
    void display();
};

/* 构造函数 */
DecisionTree::DecisionTree(int _d, int _s) :
    n_dim(_d), n_sample(_s), root(NULL)
{
    attribute = vector<string>(n_dim);
    samspc = SampleSpace(n_sample, vector<int>(n_dim + 1, 0));
    dsc = vector<map<string,int> >(n_dim + 1, map<string,int>());
    rev = vector<map<int,string> >(n_dim + 1, map<int,string>());
}

/* 析构函数 */
DecisionTree::~DecisionTree()
{
    attribute.clear();
    /* samspc 在 build() 结束时就被 clear() 了
     * samspc.clear();
     */
    dsc.clear();
    rev.clear();
    _clear(root);
}

/* 递归砍树 */
void DecisionTree::_clear(dtNode *&rt)
{
    for(int i = 0; i < rt->child.size(); ++i)
        _clear(rt->child[i]);
    delete rt;
    rt = NULL;
}

/* 输入样本空间 */
void DecisionTree::input()
{
    cout << "\nInput the sample space"
        << "\nPlease ensure that one sample per line, and the label be the last one\n"
        << endl;
    // 读入属性的名字
    for(int i = 0; i < n_dim; ++i)
        cin >> attribute[i];

    vector<vector<string> > buf =
        vector<vector<string> >(n_sample, vector<string>(n_dim + 1));
    // 读入属性值和 label
    for(int i = 0; i < n_sample; ++i)
        for(int j = 0; j <= n_dim; ++j) // including the label
            cin >> buf[i][j];
    // 离散化样本空间
    // 并存进 samspc
    _formatting(buf);
    // 字符串的样本空间已没用
    buf.clear();
}

/* 离散化样本空间 */
void DecisionTree::_formatting(const vector<vector<string> > &buf)
{
    for(int d = 0; d <= n_dim; ++d) // including the label
    {
        int cnt = 0; // 离散化标号从 1 开始
        for(int i = 0; i < n_sample; ++i)
        {
            if(!dsc[d][buf[i][d]])
            {
                dsc[d][buf[i][d]] = ++cnt;
                rev[d][cnt] = buf[i][d];
            }
            samspc[i][d] = dsc[d][buf[i][d]];
        }
    }
}

/* 建树 -> 调 _build() 来建 */
void DecisionTree::build()
{
    _build(samspc, root);
    samspc.clear();
}

/* 真·建树 */
void DecisionTree::_build(SampleSpace sp, dtNode *&rt)
{
    rt = new dtNode();
    // 如果剩下的 label 全都相同
    // 直接让这个结点成为叶子
    // 就预测为这个 label
    if(_same_class(sp))
    {
        rt->label = sp[0].back();
        return;
    }

    // 如果并不是所有 label 都相同
    // 但是已经没有可用的属性（全被删掉）
    // 那这个结点也是叶子
    // 预测的 label 是占数最多的那个 label
    int minus_cnt = 0;
    for(int i = 0; i < n_dim; ++i)
        minus_cnt += (sp[0][i] < 0 ? 1 : 0);
    // 因为删属性只是把那一列属性标成负数
    // 所以如果值为负数的列数等于总的属性数
    // 就意味着所有属性都被删了
    if(minus_cnt == n_dim) // no attribution left
    {
        rt->label = _most_label(sp);
        return;
    }

    // 选一个能获得最大信息增益的属性来分割
    rt->attr_id = _max_gain_attr(sp);
    // 理论上这个属性有多少种取值可能
    // 这个结点就有多少个子结点
    rt->n_child = dsc[rt->attr_id].size();
    // 删掉一列属性后得到一个新样本空间
    SampleSpace new_sp = _drop_attr(sp, rt->attr_id), sub;

    for(int i = 0; i < rt->n_child; ++i) // 枚举这个属性的所有可能取值
    {
        // 把样本空间中这个属性的取值是 i 的样本找出来
        // 组成一个子样本空间 sub
        for(int j = 0; j < sp.size(); ++j)
            if(sp[j][rt->attr_id] == i + 1)
                sub.push_back(new_sp[j]);
        // 如果样本空间非空
        // 那对应的子结点才真的存在
        // 递归下去建树
        if(!sub.empty())
        {
            rt->child.push_back(NULL);
            _build(sub, rt->child[rt->child.size() - 1]);
            sub.clear();
        }
    }
    // 重新数真正的子结点个数
    rt->n_child = rt->child.size();
    rt->child.resize(rt->n_child);
    // 样本空间已没用
    new_sp.clear();
    sp.clear();
}

/* 判断样本空间的样本是否都是同一个 label */
bool DecisionTree::_same_class(const SampleSpace &sp)
{
    int lb = -1;
    for(int i = 0; i < sp.size(); ++i)
        if(lb == -1)
            lb = sp[i].back();
        else if(lb != sp[i].back())
            return false;
    return true;
}

/* 找到样本空间里占数最多的那个 label */
int DecisionTree::_most_label(const SampleSpace &sp)
{
    int n_label = dsc[n_dim].size();
    int *cnt = new int[n_label + 1];
    for(int i = 0; i <= n_label; ++i)
        cnt[i] = 0;

    for(int i = 0; i < sp.size(); ++i)
        ++cnt[sp[i].back()];
    int res = 0;
    for(int i = 1; i <= n_label; ++i)
        if(cnt[i] > cnt[res])
            res = i;
    delete[] cnt;
    return res;
}

/* 找能获得最大信息增益的那个属性 */
int DecisionTree::_max_gain_attr(const SampleSpace &sp)
{
    int ans = 0;
    double big_gain = -100.0;
    for(int atr = 0; atr < sp[0].size() - 1; ++atr) // 最后一列是 label
    {
        if(sp[0][atr] < 0) // 已被删的属性不考虑
            continue;
        double g = _info_gain(sp, atr);
        if(g > big_gain)
        {
            big_gain = g;
            ans = atr;
        }
    }
    return ans;
}

/* 计算信息增益（其实只是信息熵，但效果相同） */
double DecisionTree::_info_gain(const SampleSpace &sp, int atr)
{
    double ans = 0.0;
    // label 取值种数‘属性取值种数
    int n_label = dsc[n_dim].size(), n_attr_val = dsc[atr].size();
    // 统计数组 -> 统计各种 label 取值的出现次数
    int *cnt = new int[n_label + 1];

    for(int val = 1; val <= n_attr_val; ++val)
    {
        int tot = 0;
        double ent = 0.0;
        for(int j = 0; j <= n_label; ++j)
            cnt[j] = 0;

        for(int j = 0; j < sp.size(); ++j)
            if(sp[j][atr] == val)
            {
                ++cnt[sp[j].back()];
                ++tot;
            }

        for(int j = 1; j <= n_label; ++j)
        {
            double p = (double)cnt[j] / (double)tot;
            ent -= p * log2(p); // NOT +=
        }
        ans += (double)tot / (double)sp.size() * ent;
    }
    delete[] cnt;
    return ans;
}

/* 删掉样本空间的一列属性 -> 把那一列标称负数 */
SampleSpace DecisionTree::_drop_attr(SampleSpace sp, int atr)
{
    for(int i = 0; i < sp.size(); ++i)
        sp[i][atr] = /*-sp[i][atr]*/ -1;
    return sp;
}

/* 打印决策树 */
void DecisionTree::display()
{
    cout << "--- Decision Tree ---" << endl;
    _print_tree(root, 0);
}

/* 真·打印决策树 */
void DecisionTree::_print_tree(dtNode *rt, int ind)
{
    // 缩进
    for(int i = 0; i < ind; ++i)
        cout << ' ';

    // 如果是叶子
    if(!rt->n_child)
    {
        cout << rev[n_dim][rt->label] << endl;
        return;
    }
    // 打印属性名
    cout << attribute[rt->attr_id] << endl;
    // 缩进加上属性名的长度
    ind += attribute[rt->attr_id].length();

    int len = 0, idx = rt->attr_id;
    // 找最长的字符串的长度
    for(map<int,string>::iterator it = rev[idx].begin(); it != rev[idx].end(); ++it)
        if(len < it->second.length())
            len = it->second.length();

    for(int ch = 0; ch < rt->n_child; ++ch)
    {
        for(int j = 0; j < ind; ++j)
            cout << ' ';
        cout << setw(len) << rev[rt->attr_id][ch+1] << endl;
        _print_tree(rt->child[ch], ind + len + 1);
    }
}

/*------- Main Function -------*/

int main()
{
    cout << "--- Decision Tree ---\n";
    int sam, dim;
    cout << "\nNumber of samples in the sample space: ";
    cin >> sam;
    cout << "\nNumber of dimensions: ";
    cin >> dim;
    DecisionTree x_x(dim, sam);
    x_x.input();
    x_x.build();
    system("CLS");
    x_x.display();
    system("PAUSE");
    return 0;
}