VSLAM之边缘化 Marginalization 和 FEJ (First Estimated Jocobian)
文章目录
- 1. 前言
- 2. 舒尔补 (Schur complement) 实现边缘化 (Marginalization)
- 2.1 舒尔补操作及矩阵快速求逆
- 2.2 多元高斯分布下的舒尔补分解:边际分布 (marginal distribution) 及条件分布
- 3. 视觉SLAM优化变量的边缘化
- 3.1 不丢弃优化变量的边缘化 (加速更新位姿求解)
- 3.2 丢弃优化变量的边缘化 (减少优化变量并传递边缘化先验)
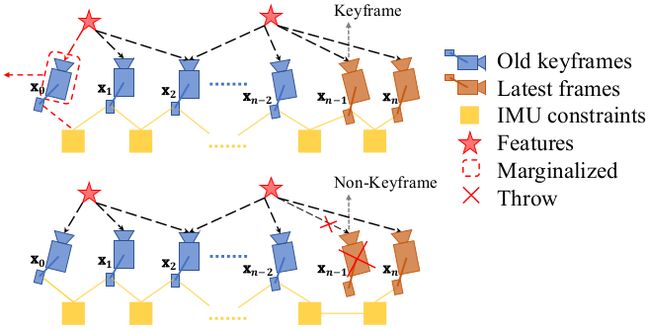
- 3.3 VINS倆种边缘化策略
- 4. First Estimate Jacobian (FEJ)
1. 前言
本博客主要介绍了VINS-Mono中边缘化的相关知识,由于VINS-Mono中只是提及了边缘化的策略并没有提及边缘化信息传递的原理,因此本博客主要参考了崔化坤的《VINS论文推导及代码解析》、深蓝学院的VIO课程以及贺博的博客SLAM中的marginalization 和 Schur complement。
VINS-Mono的边缘化与在《SLAM14讲》中提及的边缘化 (可看博客SLAM学习——后端(二)) 不同:
- 《SLAM14讲》中提及的边缘化 (G2O边缘化) 是在计算求解过程中,先消去路标点变量,实现先求解相机位姿,然后再利用求解出来的相机位姿反过来计算路标点的过程,目的是为了加速求解,并非真的将路标点给边缘化点。
- VINS-Mono的边缘化则真正需要边缘化掉滑动窗口中的最老帧或次新帧,目的是希望不再计算这一帧的位姿或者与其相关的路标点,但是希望保留该帧对窗口内其他帧的约束关系。
2. 舒尔补 (Schur complement) 实现边缘化 (Marginalization)
2.1 舒尔补操作及矩阵快速求逆
将矩阵 M = [ A B C D ] M=\begin{bmatrix} A & B \\ C & D\end{bmatrix} M=[ACBD]变成上三角或者下三角形过程中,会用到舒尔补操作: [ I 0 − C A − 1 I ] [ A B C D ] = [ A B 0 Δ A ] \begin{bmatrix} I & 0 \\ -CA^{-1} & I \end{bmatrix} \begin{bmatrix} A & B \\ C & D \end{bmatrix} = \begin{bmatrix} A & B \\ 0 & \Delta_{A}\end{bmatrix} [I−CA−10I][ACBD]=[A0BΔA] [ A B C D ] [ I − A − 1 B 0 I ] = [ A 0 C Δ A ] \begin{bmatrix}A & B \\ C & D\end{bmatrix}\begin{bmatrix} I & -A^{-1}B \\ 0 & I\end{bmatrix}=\begin{bmatrix} A & 0 \\ C & \Delta _{A}\end{bmatrix} [ACBD][I0−A−1BI]=[AC0ΔA] 其中 A A A为可逆矩阵, Δ A = D − C A − 1 B \Delta_{A}=D-CA^{-1}B ΔA=D−CA−1B,称为A关于M的舒尔补,联合起来,将M变形成对角矩阵: [ I 0 − C A − 1 I ] [ A B C D ] [ I − A − 1 B 0 I ] = [ A 0 0 Δ A ] \begin{bmatrix} I & 0 \\ -CA^{-1} & I \end{bmatrix} \begin{bmatrix} A & B \\ C & D \end{bmatrix} \begin{bmatrix} I & -A^{-1}B \\ 0 & I\end{bmatrix}=\begin{bmatrix} A & 0 \\ 0 & \Delta _{A}\end{bmatrix} [I−CA−10I][ACBD][I0−A−1BI]=[A00ΔA] 反过来又能从对角矩阵恢复成矩阵 M M M: [ I 0 C A − 1 I ] [ A 0 0 Δ A ] [ I A − 1 B 0 I ] = [ A B C D ] \begin{bmatrix} I & 0 \\ CA^{-1} & I \end{bmatrix}\begin{bmatrix} A & 0 \\ 0 & \Delta _{A}\end{bmatrix} \begin{bmatrix} I & A^{-1}B \\ 0 & I\end{bmatrix} = \begin{bmatrix} A & B \\ C & D \end{bmatrix} [ICA−10I][A00ΔA][I0A−1BI]=[ACBD] 以上变换均建立在矩阵 A A A可逆的前提下,如果矩阵 A A A不可逆而矩阵 D D D可逆,同样可以进行舒尔补操作将 M M M矩阵变为上三角或者下三角的形式: [ I − B D − 1 0 I ] [ A B C D ] = [ Δ D 0 C D ] \begin{bmatrix} I & -BD^{-1} \\ 0 & I \end{bmatrix} \begin{bmatrix} A & B \\ C & D \end{bmatrix} = \begin{bmatrix} \Delta_{D} & 0 \\ C & D \end{bmatrix} [I0−BD−1I][ACBD]=[ΔDC0D] 其中 Δ D = A − B D − 1 C \Delta_{D}=A-BD^{-1}C ΔD=A−BD−1C,称为 D D D关于 M M M的舒尔补。
舒尔补操作在实现将矩阵 M M M分解为上三角下三角形式的同时,也实现了矩阵M的快速求逆: M = [ A B C D ] = [ I 0 C A − 1 I ] [ A 0 0 Δ A ] [ I A − 1 B 0 I ] M=\begin{bmatrix}A & B \\ C & D \end{bmatrix}=\begin{bmatrix}I & 0 \\CA^{-1} & I \end{bmatrix} \begin{bmatrix} A & 0 \\ 0 & \Delta_{A}\end{bmatrix}\begin{bmatrix} I & A^{-1}B \\ 0 & I\end{bmatrix} M=[ACBD]=[ICA−10I][A00ΔA][I0A−1BI] 求逆可得: M − 1 = [ A B C D ] − 1 = [ I − A − 1 B 0 I ] [ A − 1 0 0 Δ A − 1 ] [ I 0 − C A − 1 I ] M^{-1}=\begin{bmatrix}A & B \\ C & D\end{bmatrix}^{-1}=\begin{bmatrix}I & -A^{-1}B \\ 0 & I\end{bmatrix} \begin{bmatrix} A^{-1}& 0 \\ 0 & \Delta_{A}^{-1}\end{bmatrix} \begin{bmatrix} I & 0 \\ -CA^{-1} & I \end{bmatrix} M−1=[ACBD]−1=[I0−A−1BI][A−100ΔA−1][I−CA−10I] 其中 [ I − A − 1 B 0 I ] [ I A − 1 B 0 I ] = I \begin{bmatrix}I & -A^{-1}B \\ 0 & I\end{bmatrix}\begin{bmatrix}I & A^{-1}B \\ 0 & I\end{bmatrix}=I [I0−A−1BI][I0A−1BI]=I
2.2 多元高斯分布下的舒尔补分解:边际分布 (marginal distribution) 及条件分布
假设多元变量服从零均值高斯分布 P ( α , β ) P(\alpha, \beta) P(α,β),且由俩部分组成: x = [ α β ] \mathbf{x}=\begin{bmatrix} \alpha \\ \beta \end{bmatrix} x=[αβ],变量之间构成的协方差矩阵为: K = [ A C T C D ] (1) K=\begin{bmatrix} A & C^{T} \\ C & D\end{bmatrix} \tag{1} K=[ACCTD](1) 其中 A = c o v ( α , α ) A=cov(\alpha, \alpha) A=cov(α,α), D = c o v ( β , β ) D=cov(\beta, \beta) D=cov(β,β), C = c o v ( α , β ) C=cov(\alpha, \beta) C=cov(α,β),由此变量 x x x的分布为: P ( α , β ) = P ( α ) P ( β ∣ α ) ∝ e x p ( − 1 2 [ α β ] T [ A C T C D ] − 1 [ α β ] ) ∝ e x p ( − 1 2 [ α β ] T [ I − A − 1 C T 0 I ] [ A − 1 0 0 Δ A − 1 ] [ I 0 − C A − 1 I ] [ α β ] ) ∝ e x p ( − 1 2 [ α T ( β − C A − 1 α ) T ] [ A − 1 0 0 Δ A − 1 ] [ α β − C A − 1 α ] ) ∝ e x p ( − 1 2 ( α T A − 1 α ) + ( β − C A − 1 α ) T Δ A − 1 ( β − C A − 1 α ) ) ∝ e x p ( − 1 2 α T A − 1 α ) ⏟ P ( α ) e x p ( − 1 2 ( β − C A − 1 α ) T Δ A − 1 ( β − C A − 1 α ) ) ⏟ P ( β ∣ α ) (2) P(\alpha,\beta)=P(\alpha)P(\beta|\alpha) \propto exp(-\frac{1}{2}\begin{bmatrix} \alpha \\ \beta \end{bmatrix}^{T}\begin{bmatrix} A & C^{T} \\ C & D\end{bmatrix}^{-1}\begin{bmatrix} \alpha \\ \beta \end{bmatrix}) \\ \propto exp(-\frac{1}{2} \begin{bmatrix} \alpha \\ \beta \end{bmatrix}^{T} \begin{bmatrix}I & -A^{-1}C^{T} \\ 0 & I\end{bmatrix} \begin{bmatrix} A^{-1}& 0 \\ 0 & \Delta_{A}^{-1}\end{bmatrix} \begin{bmatrix} I & 0 \\ -CA^{-1} & I \end{bmatrix}\begin{bmatrix} \alpha \\ \beta \end{bmatrix}) \\ \propto exp(-\frac{1}{2}\begin{bmatrix}\alpha^{T} & (\beta-CA^{-1}\alpha)^{T}\end{bmatrix}\begin{bmatrix} A^{-1}& 0 \\ 0 & \Delta_{A}^{-1}\end{bmatrix}\begin{bmatrix} \alpha & \beta-CA^{-1}\alpha\end{bmatrix}) \\ \propto exp(-\frac{1}{2}(\alpha^{T}A^{-1}\alpha)+(\beta-CA^{-1}\alpha)^{T}\Delta_{A}^{-1}(\beta-CA^{-1}\alpha)) \\ \propto \underset{P(\alpha)}{\underbrace{exp(-\frac{1}{2}\alpha^{T}A^{-1}\alpha)}}\underset{P(\beta|\alpha)}{\underbrace{exp(-\frac{1}{2}(\beta-CA^{-1}\alpha)^{T}\Delta_{A}^{-1}(\beta-CA^{-1}\alpha))}} \tag{2} P(α,β)=P(α)P(β∣α)∝exp(−21[αβ]T[ACCTD]−1[αβ])∝exp(−21[αβ]T[I0−A−1CTI][A−100ΔA−1][I−CA−10I][αβ])∝exp(−21[αT(β−CA−1α)T][A−100ΔA−1][αβ−CA−1α])∝exp(−21(αTA−1α)+(β−CA−1α)TΔA−1(β−CA−1α))∝P(α) exp(−21αTA−1α)P(β∣α) exp(−21(β−CA−1α)TΔA−1(β−CA−1α))(2)
意味着通过舒尔补操作能从高斯联合分布 P ( α , β ) P(\alpha,\beta) P(α,β)分解出边际分布 P ( α ) P(\alpha) P(α) (边缘掉了 β \beta β)和条件分布 P ( β ∣ α ) P(\beta|\alpha) P(β∣α)。可以看出边际分布的协方差为 A A A,即为从联合分布中取对应的矩阵块,而条件分布的协方差为 Δ A \Delta_{A} ΔA,即 A A A对应的舒尔补 D − C A − 1 B D-CA^{-1}B D−CA−1B,均值也变了。
在SLAM的优化问题中,我们往往操作的是信息矩阵,而不是协方差矩阵,因此需要计算边际分布和条件分布对应的信息矩阵:
对于高斯联合分布 P ( a , β ) P(a, \beta) P(a,β)的信息矩阵,由于信息矩阵等于协方差矩阵的逆,根据公式 ( 1 ) ( 2 ) (1)(2) (1)(2)我们有: [ A C T C D ] − 1 = [ A − 1 + A − 1 C T Δ A − 1 C A − 1 − A − 1 C T Δ A − 1 − C A − 1 Δ A − 1 Δ A − 1 ] = [ Λ α α Λ α β Λ β α Λ β β ] \begin{bmatrix} A & C^{T} \\ C & D\end{bmatrix}^{-1} = \begin{bmatrix} A^{-1}+A^{-1}C^{T}\Delta_{A}^{-1}CA^{-1} & -A^{-1}C^{T}\Delta_{A}^{-1} \\ -CA^{-1}\Delta A^{-1} & \Delta_{A}^{-1}\end{bmatrix} = \begin{bmatrix} \Lambda_{\alpha \alpha} & \Lambda_{\alpha \beta} \\ \Lambda_{\beta \alpha} & \Lambda_{\beta\beta} \end{bmatrix} [ACCTD]−1=[A−1+A−1CTΔA−1CA−1−CA−1ΔA−1−A−1CTΔA−1ΔA−1]=[ΛααΛβαΛαβΛββ] 由于条件分布 P ( β ∣ α ) P(\beta|\alpha) P(β∣α)和边际分布 P ( α ) P(\alpha) P(α)的协方差矩阵分别为 Δ A \Delta_{A} ΔA、 A A A,故其信息矩阵分别为: Δ A − 1 = Λ β β , A − 1 = Λ α α − Λ α β Λ β β − 1 Λ β α (3) \Delta_{A}^{-1} = \Lambda_{\beta \beta} \ , \ A^{-1}=\Lambda_{\alpha \alpha}-\Lambda_{\alpha \beta}\Lambda^{-1}_{\beta \beta}\Lambda_{\beta \alpha} \tag{3} ΔA−1=Λββ , A−1=Λαα−ΛαβΛββ−1Λβα(3)
对于非零矩阵的高斯分布 P ( α , β ) = N ( [ μ α μ β ] , [ Σ α α , Σ a β Σ β α , Σ β β ] ) = N − 1 ( [ η α η β ] , [ Λ α α Λ α β Λ β α Λ β β ] ) P(\alpha, \beta)=\mathcal{N}(\begin{bmatrix} \mu_{\alpha} \\ \mu_{\beta}\end{bmatrix}, \begin{bmatrix} \Sigma_{\alpha \alpha}, \Sigma_{a \beta} \\ \Sigma_{\beta \alpha}, \Sigma_{\beta \beta} \end{bmatrix}) = \mathcal{N}^{-1}(\begin{bmatrix} \eta_{\alpha} \\ \eta_{\beta} \end{bmatrix}, \begin{bmatrix} \Lambda_{\alpha \alpha} & \Lambda_{\alpha \beta} \\ \Lambda_{\beta \alpha} & \Lambda_{\beta \beta}\end{bmatrix}) P(α,β)=N([μαμβ],[Σαα,ΣaβΣβα,Σββ])=N−1([ηαηβ],[ΛααΛβαΛαβΛββ]),
分解出的边际分布 (Marginalization) P ( α ) P(\alpha) P(α) (边缘掉了 β \beta β) 和条件分布 (Conditioning) P ( α ∣ β ) P(\alpha|\beta ) P(α∣β) (注意我们前面的推导是 P ( β ∣ α ) P(\beta|\alpha) P(β∣α)) 对应的协方差矩阵 (Covariance Form) 和信息矩阵 (Information Form) 如下:

3. 视觉SLAM优化变量的边缘化
3.1 不丢弃优化变量的边缘化 (加速更新位姿求解)
在视觉SLAM中Bundle Adjustment优化相机和位姿时,构建的非线性最小二乘问题可以通过高斯牛顿迭代获得,即 H δ x = b H \delta x = b Hδx=b, 这里的 H H H矩阵 (通过 Σ \Sigma Σ范数构建的残差项) 也是本文所提及的信息矩阵,由于 H H H矩阵具备稀疏性,其结构一般如下:
构建的方程为: [ Λ a Λ b Λ b T Λ c ] [ δ x a δ x b ] = [ g a g b ] (4) \begin{bmatrix} \Lambda_{a} & \Lambda_{b} \\ \Lambda_{b}^{T} & \Lambda c\end{bmatrix} \begin{bmatrix} \delta x_{a} \\ \delta x_{b} \end{bmatrix} = \begin{bmatrix} g_{a} \\ g_{b}\end{bmatrix} \tag{4} [ΛaΛbTΛbΛc][δxaδxb]=[gagb](4) 假如这里我们要边缘化掉 δ x b \delta x_{b} δxb,通过舒尔补对上面方程进行消元得: [ Λ a − Λ b Λ c − 1 Λ b T 0 Λ b T Λ c ] [ δ x a δ x b ] = [ g a − Λ b Λ c − 1 g b g b ] \begin{bmatrix} \Lambda_{a}-\Lambda_{b}\Lambda_{c}^{-1}\Lambda_{b}^{T} & 0 \\ \Lambda_{b}^{T} & \Lambda_{c}\end{bmatrix} \begin{bmatrix} \delta x_{a} \\ \delta x_{b} \end{bmatrix} = \begin{bmatrix} g_{a}- \Lambda_{b}\Lambda_{c}^{-1} g_{b}\\ g_{b}\end{bmatrix} [Λa−ΛbΛc−1ΛbTΛbT0Λc][δxaδxb]=[ga−ΛbΛc−1gbgb] 此时关于 δ a \delta a δa的方程为: ( Λ a − Λ b Λ c − 1 Λ b T ) δ x a = g a − Λ b Λ c − 1 g b (\Lambda_{a}-\Lambda_{b}\Lambda_{c}^{-1}\Lambda_{b}^{T})\delta x_{a} = g_{a}-\Lambda_{b}\Lambda_{c}^{-1}g_{b} (Λa−ΛbΛc−1ΛbT)δxa=ga−ΛbΛc−1gb 关于变量$ δ x a \delta x_{a} δxa的信息矩阵为: A − 1 = Λ a − Λ b Λ c − 1 Λ b T A^{-1}= \Lambda_{a}-\Lambda_{b}\Lambda_{c}^{-1}\Lambda_{b}^{T} A−1=Λa−ΛbΛc−1ΛbT, 与公式 ( 3 ) (3) (3)一致。
假如要边缘掉 δ x a \delta x_{a} δxa, 通过舒尔补对方程 ( 4 ) (4) (4) 进行消元得: [ Λ a Λ b 0 Λ c − Λ b T Λ a − 1 Λ b ] [ δ x a δ x b ] = [ g a g b − Λ b T Λ a − 1 g a ] \begin{bmatrix} \Lambda_{a} & \Lambda_{b} \\ 0 & \Lambda_{c}-\Lambda_{b}^{T}\Lambda_{a}^{-1}\Lambda_{b} \end{bmatrix} \begin{bmatrix} \delta x_{a} \\ \delta x_{b} \end{bmatrix} = \begin{bmatrix} g_{a} \\ g_{b}- \Lambda_{b}^{T}\Lambda_{a}^{-1} g_{a}\end{bmatrix} [Λa0ΛbΛc−ΛbTΛa−1Λb][δxaδxb]=[gagb−ΛbTΛa−1ga] 此时关于 δ b \delta b δb的方程为: ( Λ c − Λ b T Λ a − 1 Λ b ) δ x b = g b − Λ b T Λ a − 1 g a (\Lambda_{c}-\Lambda_{b}^{T}\Lambda_{a}^{-1}\Lambda_{b})\delta x_{b} = g_{b}- \Lambda_{b}^{T}\Lambda_{a}^{-1} g_{a} (Λc−ΛbTΛa−1Λb)δxb=gb−ΛbTΛa−1ga 关于变量 δ x b \delta x_{b} δxb的信息矩阵为: B − 1 = ( Λ c − Λ b T Λ a − 1 Λ b ) (5) B^{-1} =(\Lambda_{c}-\Lambda_{b}^{T}\Lambda_{a}^{-1}\Lambda_{b}) \tag{5} B−1=(Λc−ΛbTΛa−1Λb)(5)
上述俩种操作由于边缘化的变量不同,导致后面得到的信息矩阵亦不同,因此在边缘化中应明确保留的变量和边缘化掉的变量。
在上面这个过程中,我们要注意,构建出来的 H x = b Hx=b Hx=b是利用了边缘化变量的信息,也就是说我们没有人为的丢弃约束,所以不会丢失信息,但是计算结果的时候,我们只去更新了我们希望保留的那些变量的值。
3.2 丢弃优化变量的边缘化 (减少优化变量并传递边缘化先验)
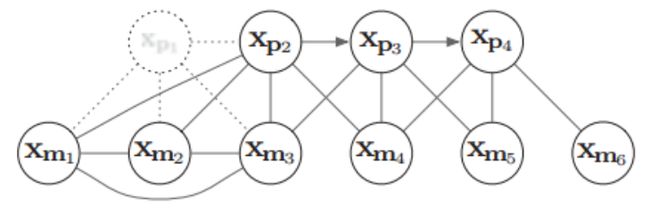
下面用一个具体例子来形象说明边缘化过程及其导致的矩阵稠密现象(fill-in)。假设有4个相机位姿 x p t x_{pt} xpt,以及6个路标点 x m k x_{mk} xmk (路标点用 x y z xyz xyz的参数化),相机与路标点的边表示一次观测,相邻相机之间的边表示IMU约束,相互关系如下:
下面试图将 x p 1 x_{p1} xp1给marg (边缘化) 掉,然后再将 x m 1 x_{m1} xm1给marg掉,看看信息矩阵H会如何变化:
其中,图(2-a)表示原始的 H H H矩阵,注意这里的左上角为路标点相关部分,而左上角是Pose的相关部分,图(2-b)是把 H H H矩阵中跟 x p 1 x_{p1} xp1相关的部分移动到 H H H矩阵的左上角,详细表示如下:
当将 H H H矩阵关于Pose1 x p 1 x_{p1} xp1 的相关部分移到左上角后,根据图4 H H H 矩阵的变量的分布情况构建与公式(4)类似的矩阵等式: [ Λ a 6 × 6 Λ b 6 × 36 Λ b T 36 × 6 Λ c 36 × 36 ] [ δ x a 6 × 1 δ x b 36 × 1 ] = [ g a 6 × 1 g b 36 × 1 ] (6) \begin{bmatrix} {\Lambda_{a}}^{6 \times 6} & {\Lambda_{b}}^{6 \times 36} \\ {\Lambda_{b}^{T}}^{36 \times6} & {\Lambda c}^{36 \times 36}\end{bmatrix} \begin{bmatrix} {\delta x_{a}}^{6 \times 1} \\ {\delta x_{b}}^{36 \times 1} \end{bmatrix} = \begin{bmatrix} {g_{a}}^{6 \times 1} \\ {g_{b}}^{36 \times 1}\end{bmatrix} \tag{6} [Λa6×6ΛbT36×6Λb6×36Λc36×36][δxa6×1δxb36×1]=[ga6×1gb36×1](6) 我们通过舒尔补操作将 x p 1 x_{p1} xp1边缘化,即为公式 ( 5 ) (5) (5)对应的 ( Λ c − Λ b T Λ a − 1 Λ b ) (\Lambda_{c}-\Lambda_{b}^{T}\Lambda_{a}^{-1}\Lambda_{b}) (Λc−ΛbTΛa−1Λb),得到新的信息矩阵 H n e w H_{new} Hnew即为 ( Λ c − Λ b T Λ a − 1 Λ b ) (\Lambda_{c}-\Lambda_{b}^{T}\Lambda_{a}^{-1}\Lambda_{b}) (Λc−ΛbTΛa−1Λb),相比于原来的信息矩阵,新的信息矩阵更加稠密,即marg掉一个pose后,会使得 H n e w H_{new} Hnew有3个地方被fill-in, 如下黄色区域:
这时图关系则变为:
观察图6可知, x m 1 x_{m1} xm1、 x m 2 x_{m2} xm2和 x m 3 x_{m3} xm3彼此之间已经产生了新的约束关系,且 x p 2 x_{p2} xp2和 m 1 m_{1} m1产生了新的关系。因此,原先条件独立的变量,在边缘化某些变量之后,可能变得相关。
紧接着marg掉路标点 x m 1 x_{m_{1}} xm1,新的信息矩阵变量的约束关系如下图:
对应的图关系如下:
可以发现,marg 掉 x m 1 x_{m1} xm1后,并没有使H矩阵更稠密,这是因为 x m 1 x_{m1} xm1之前并未与其他pose有约束关系,即并未被观察到,因此如果marg掉那些不被其他帧观察到的路标点,不会显著使信息矩阵H变得稠密。而要marg掉的路标点中,对于那些被其他帧观测到的路标点,要么就别设置为marg,要么就宁愿丢弃,这是OKVIS和DSO中用到的策略。
3.3 VINS倆种边缘化策略
VINS根据次新帧是否为关键帧,分为倆种边缘化策略:通过对比次新帧和次次新帧的视差量,来决定marg掉次新帧或者最老帧:(由于这部分理论已在上面讲完,待补充代码讲解部分)
- 当次新帧为关键帧时,MARGIN_OLD,将 marg 掉最老帧,及其看到的路标点和相关联的 IMU 数据,将其转化为先验信息加到整体的目标函数中。
- 当次新帧不是关键帧时,MARGIN_SECOND_NEW,我们将直接扔掉次新帧及它的视觉观测边,而不对次新帧进行 marg,因为我们认为当前帧和次新帧很相似,也就是说当前帧跟路标点之间的约束和次新帧与路标点的约束很接近,直接丢弃并不会造成整个约束关系丢失过多信息。但是值得注意的是,我们要保留次新帧的 IMU 数据,从而保证 IMU 预积分的连贯性。
4. First Estimate Jacobian (FEJ)
举一个简单的例子引出新测量信息和旧测量信息构建的增量方程的解所存在的问题:
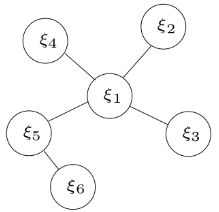
假如有5个相机位姿 ξ i \xi_{i} ξi,每个相机位姿与其他相机构建的残差用边表示,有一元边,二元边,多元边等,相机之间的关系如下所示:
通过误差项和信息矩阵得到的优化变量的信息矩阵为: Λ m ( k ) = ∑ ( i , j ) ∈ S m J i j T ( k ) Σ i j − 1 J i j ( k ) = [ Λ β β ( k ) Λ β α ( k ) Λ α β ( k ) Λ α α ( k ) ] (7) \Lambda_{m}(k) = \underset{(i,j)\in S_{m}}{\sum} J^{T}_{ij}(k) \Sigma_{ij}^{-1}J_{ij}(k) = \begin{bmatrix} \Lambda_{\beta \beta}(k) & \Lambda_{\beta \alpha}(k) \\ \Lambda_{\alpha \beta}(k) & \Lambda_{\alpha \alpha}(k) \end{bmatrix} \tag{7} Λm(k)=(i,j)∈Sm∑JijT(k)Σij−1Jij(k)=[Λββ(k)Λαβ(k)Λβα(k)Λαα(k)](7) b m ( k ) = [ b β β ( k ) b β α ( k ) ] = − ∑ ( i , j ) ∈ S m J i j T ( k ) Σ i j − 1 r i j (8) b_{m}(k) = \begin{bmatrix} b_{\beta \beta}(k) \\ b_{\beta \alpha}(k) \end{bmatrix} = -\underset{(i,j) \in S_{m}}{\sum} J^{T}_{ij}(k)\Sigma_{ij}^{-1}r_{ij} \tag{8} bm(k)=[bββ(k)bβα(k)]=−(i,j)∈Sm∑JijT(k)Σij−1rij(8) 其中 ( k ) (k) (k)代表在 k k k时刻下误差项对变量的雅克比, S m S_{m} Sm代表所有的误差边, Λ m ( k ) \Lambda_{m}(k) Λm(k)代表 k k k时刻下的信息矩阵,根据之前的边缘化操作,我们marg掉 ξ 1 \xi_{1} ξ1,信息矩阵的变换如下所示:
marg掉 ξ 1 \xi_{1} ξ1后, ξ 1 \xi_{1} ξ1的测量信息传递给了剩余的变量:
b p ( k ) = b β α ( k ) − Λ α β ( k ) Λ β β − 1 ( k ) b β β ( k ) (9) b_{p}(k) = b_{\beta \alpha}(k)-\Lambda_{\alpha \beta}(k) \Lambda_{\beta \beta}^{-1}(k) b_{\beta \beta}(k) \tag{9} bp(k)=bβα(k)−Λαβ(k)Λββ−1(k)bββ(k)(9) Λ p ( k ) = Λ α α ( k ) − Λ α β ( k ) Λ β β − 1 ( k ) Λ β α ( k ) (10) \Lambda_{p}(k) = \Lambda_{\alpha \alpha}(k) - \Lambda_{\alpha \beta}(k) \Lambda_{\beta \beta}^{-1}(k) \Lambda_{\beta \alpha}(k) \tag{10} Λp(k)=Λαα(k)−Λαβ(k)Λββ−1(k)Λβα(k)(10) 其中小标 p p p表示prior (先验) 。
实际上, 我们可以从 b p ( k ) b_{p}(k) bp(k), Λ p ( k ) \Lambda_{p}(k) Λp(k)分解出一个残差 r p ( k ) r_{p}(k) rp(k)和对应的雅克比矩阵 J p ( k ) J_{p}(k) Jp(k),因为 b p ( k ) b_{p}(k) bp(k), Λ p ( k ) \Lambda_{p}(k) Λp(k)也服从 Λ p ( k ) δ ξ = J p ( k ) T Σ − 1 J p ( k ) = − J p T Σ − 1 r p ( k ) = b p ( k ) \Lambda_{p}(k) \delta \xi = J_{p}(k)^{T}\Sigma^{-1}J_{p}(k)= -J_{p}^{T}\Sigma^{-1}r_{p}(k) = b_{p}(k) Λp(k)δξ=Jp(k)TΣ−1Jp(k)=−JpTΣ−1rp(k)=bp(k),其中 δ ξ \delta \xi δξ为marg掉 ξ 1 \xi_{1} ξ1剩余的变量。
需要注意的是,由于剩余变量的不断优化,残差 r p ( k ) r_{p}(k) rp(k)或者 b p ( k ) b_{p}(k) bp(k)会跟着变化,但是雅克比 J p ( k ) J_{p}(k) Jp(k)取固定不变了。
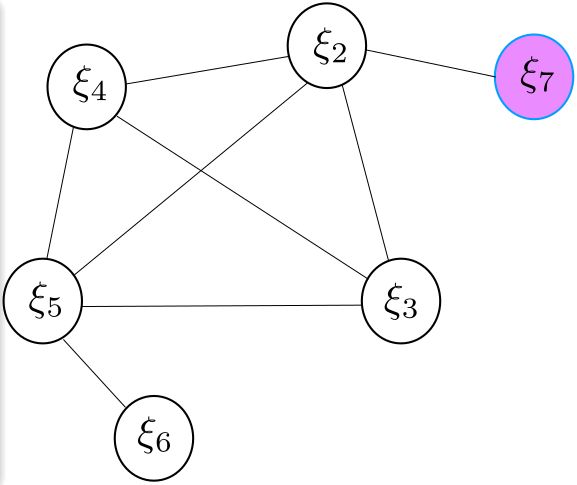
当引入新的位姿 ξ 7 \xi_{7} ξ7时,假如 ξ 7 \xi_{7} ξ7与 ξ 1 \xi_{1} ξ1有共同的观测因此可以构建新的残差项,则各个相机的位姿图关系及其信息矩阵的变化如下:
在 k ′ k' k′时刻,由于引入了新的位姿 ξ 7 \xi_{7} ξ7,因此新的残差 r 27 r_{27} r27和先验信息 b p ( k ) b_{p}(k) bp(k), Λ p ( k ) \Lambda_{p}(k) Λp(k)构建新的最小二乘问题: b ( k ′ ) = Π T J p ( k ) r p ( k ′ ) − J 2 , 7 T ( k ′ ) Σ 2 , 7 − 1 r 2 , 7 ( k ′ ) (11) b(k')=\Pi^{T}J_{p}(k)r_{p}(k') - J_{2,7}^{T}(k')\Sigma_{2,7}^{-1}r_{2,7}(k') \tag{11} b(k′)=ΠTJp(k)rp(k′)−J2,7T(k′)Σ2,7−1r2,7(k′)(11) Λ ( k ′ ) = Π T Λ p ( k ) Π + J 2 , 7 T ( k ′ ) Σ 2 , 7 − 1 J 2 , 7 ( k ′ ) (12) \Lambda(k') = \Pi^{T}\Lambda_{p}(k)\Pi + J_{2,7}^{T}(k')\Sigma_{2,7}^{-1}J_{2,7}(k') \tag{12} Λ(k′)=ΠTΛp(k)Π+J2,7T(k′)Σ2,7−1J2,7(k′)(12) 其中 Π = [ I d i m J p ( k ) , 0 ] \Pi=[I_{dim J_{p}(k)}, \ 0] Π=[IdimJp(k), 0] 用来将矩阵的维度扩张, J p ( k ) J_{p}(k) Jp(k)为先验部分对应的雅克比矩阵, r 2 , 7 ( k ′ ) r_{2,7}(k') r2,7(k′)和 J 2 , 7 ( k ′ ) J_{2,7}(k') J2,7(k′)分别表示新残差和新残差 r 27 r_{27} r27对姿态 ξ 2 \xi{2} ξ2和 ξ 7 \xi{7} ξ7的雅克比矩阵。
1. 新测量信息和旧测量信息构建的增量方程的解会存在什么问题?
- 由于被marg的变量 ξ 1 \xi_{1} ξ1 以及对应的测量已被丢弃,先验信息 Λ p ( k ) \Lambda_{p}(k) Λp(k)中关于位姿 ξ 2 \xi_{2} ξ2、 ξ 3 \xi_{3} ξ3、 ξ 4 \xi_{4} ξ4和 ξ 5 \xi_{5} ξ5在后续求解中没法更新,而对于 ξ 6 \xi_{6} ξ6是可以更新的,因为在marg掉 ξ 1 \xi_{1} ξ1之前, ξ 1 \xi_{1} ξ1和 ξ 6 \xi_{6} ξ6并没有产生共同观测。
- 而 ξ 2 \xi_{2} ξ2 (实际中可能有多个情况) 与新引入的 ξ 7 \xi_{7} ξ7产生了新的观测,这意味着新的残差 r 27 r_{27} r27对 ξ 2 \xi_{2} ξ2的雅克比是在 k ′ k' k′时刻下 ξ 2 \xi_{2} ξ2的位姿处进行线性化的。
- 因此在滑动窗口优化的时候,信息矩阵如公式(12)是由俩部分组成的,而且这俩部分计算雅克比时的线性化点不同 (在这个例子中体现在 ξ 2 \xi_{2} ξ2处线性化的地方不同 ),这可能会导致信息矩阵的零空间发生变化,从而在求解时引入错误信息。
2. SLAM系统中增量方程中的信息矩阵会存在零空间的情况?
单目 SLAM 系统 7 自由度不可观: 6 自由度姿态 (单目SLAM系统没有对齐东北天坐标系,因此整条SLAM的轨迹可移动) + 尺度 (单目SLAM存在尺度不确定性)。
单目 + IMU 系统是 4 自由度不可观: yaw 角 + 3 自由度位置不可观。roll 和 pitch 由于重力向量的存在而可观 (由于重力向量的存在,可知道轨迹与东北天坐标系在roll 和 pitch的相对方向,由于yaw可以绕重力向量旋转,故yaw不客观),尺度因子由于加速度计的存在而可观。
3. 为什么雅克比线性化点不同会导致零空间发生变化?
这个时候要拿出这张广为流传的图了(感谢泡泡机器人):
- 四张能量图中,第一张是说明能量函数 E 由两个同样的非线性函数 E 1 E_{1} E1 和 E 2 E_{2} E2 组成,我们令函数 E = 0 E=0 E=0,这时方程的解为 x y = 1 xy=1 xy=1,对应图中深蓝色的一条曲线。第二张能量函数图中的 E 1 ′ E_{1}' E1′对应函数 E 1 E_{1} E1 在点 ( 0.5 , 1.4 ) (0.5,1.4) (0.5,1.4)处的二阶泰勒展开,第三张能量函数图中的 E 2 ′ E_{2}' E2′对应函数 E 2 E2 E2 在点 ( 1.2 , 0.5 ) (1.2,0.5) (1.2,0.5)处的二阶泰勒展开。注意这两个近似的能量函数 E 2 ′ E_{2}' E2′和 E 1 ′ E_{1}' E1′是在不同的线性点附近对原函数展开得到的。最后一张图就是把这个近似得到的能量函数合并起来,对整个系统 E E E 的二阶近似。
- 从第四个能量函数图中,我们发现一个大问题,能量函数为 0 的解由以前的一条曲线变成了一个点,不确定性的东西变得确定了,专业的术语叫不可观的状态变量变得可观了,说明我们人为的引入了错误的信息。 这个实验的实质在于,在不同的点线性化后,强行加起来,实际上引入了一些人为的约束,或者说引入了人为的“错误观测”,导致整个系统的崩溃。
- 对应到 marg 的问题上,本来我们是在最初(initial)那个点附近进行线性化,但是在 marg 的过程, initial 那个点变了,它一开始是有未 marg 的点的, marg 之后,把那些点的信息给了留下的那些点,这就使得剩下那些点进行了一些偏移, 他们和之前的状态不同了,这个时候再线性化,就会导致在不同的地方进行了线性化,这样就会像上面那个例子一样,引入了错误的信息,导致整个优化过程的崩溃。因此, marg 时,被 marg 的那些变量的雅克比已经不更新了,而此时留在滑动窗口里的其他变量的雅克比要用和 marg 时一样的线性点,就是 FEJ去算,不要用新的线性点了。
最后引出解决方法FEJ:
FEJ 算法:不同残差对同一个状态求雅克比时,线性化点必须一致,这样就能避免零空间退化而使得不可观变量变得可观。在上面的例子中我们计算 r 27 r_{27} r27对姿态 ξ 2 \xi_{2} ξ2的雅克比时,线性化点必须和 r 12 r_{12} r12对齐求导一致。
但是, VINS 中并未使用 FEJ 的策略, 这里我们进行简要说明: 对于滑窗内剩余的优化变量, 如倒数第二帧位姿 T1,当边缘化掉最老帧 T0 后,会给 T1 加上新的约束。值得注意的是, 这个新约束的线性化点是在 marg 掉 T0 时刻的 T1 的值,而当之后 T1 迭代更新后,该marg 产生的约束并不会调整线性化点,即不会在新的 T1 处重新展开,这样会导致两次的线性化点不一致。 但据作者描述因未发现明显的 yaw 不可观性变化导致的轨迹漂移, 因此并未采用 FEJ 策略,反而加入 FEJ 后导致结果不佳。