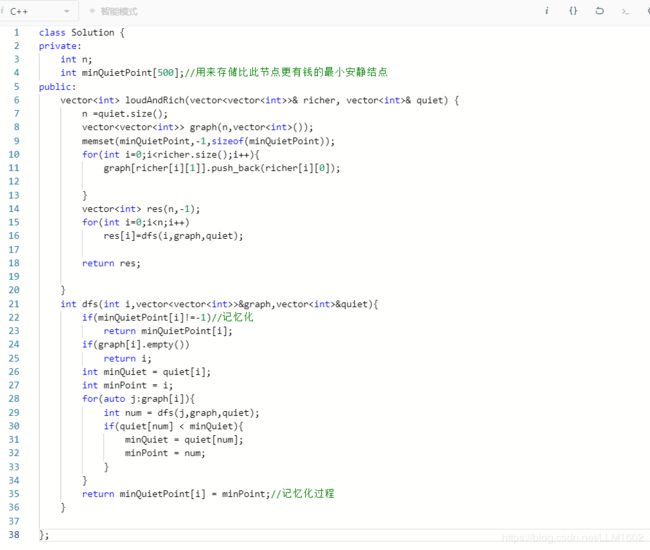
leetcode-dfs总结
一：二分图：颜色分图
1: leetcode:785 https://leetcode-cn.com/problems/is-graph-bipartite/
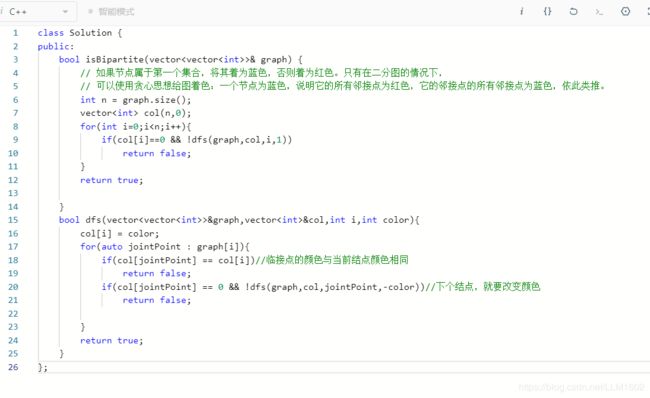
思想：即然要分成两组，二分，即颜色不同，把一天边的两个结点分成A,B两个集合，则考虑用一个颜色（eg:蓝色）赋予当 前结点，把与它相邻的结点赋予另一颜色（eg:红色），采用dfs，一个个结点dfs，只要遇到即将访问结点与当前点 颜色相同则，说明冲突，无法二分。
代码：
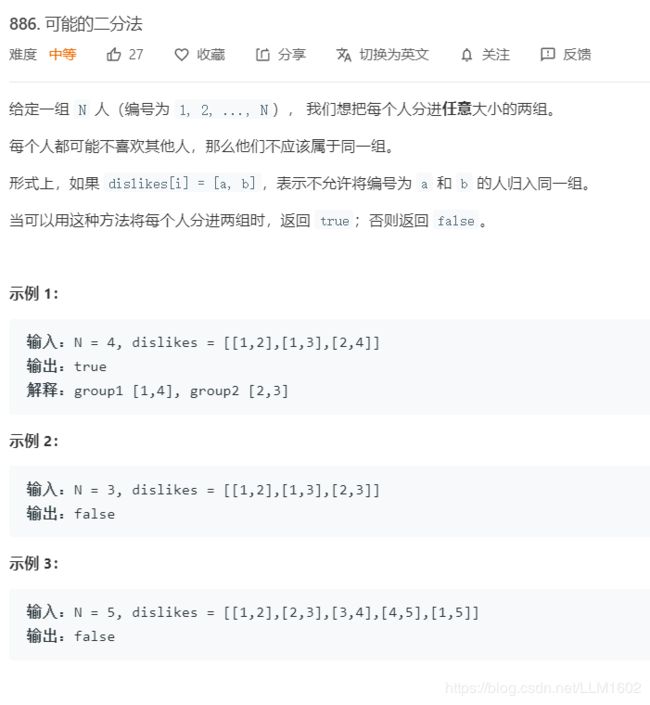
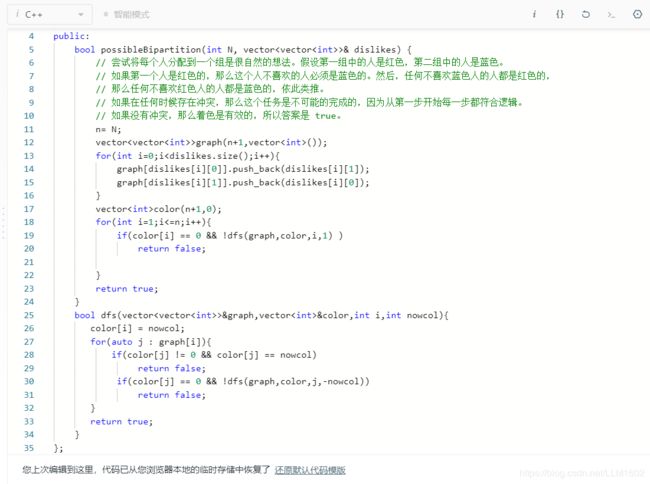
2：leetcode886:https://leetcode-cn.com/problems/possible-bipartition/
代码：
二：判断图是否有环，或者计算连通图的个数
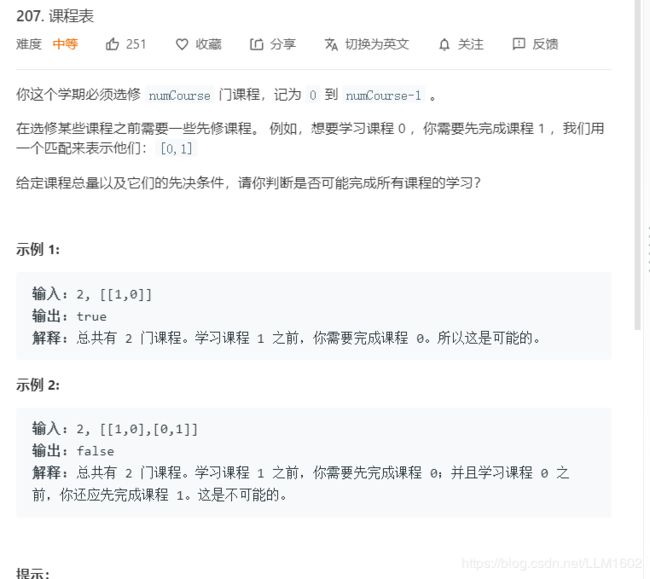
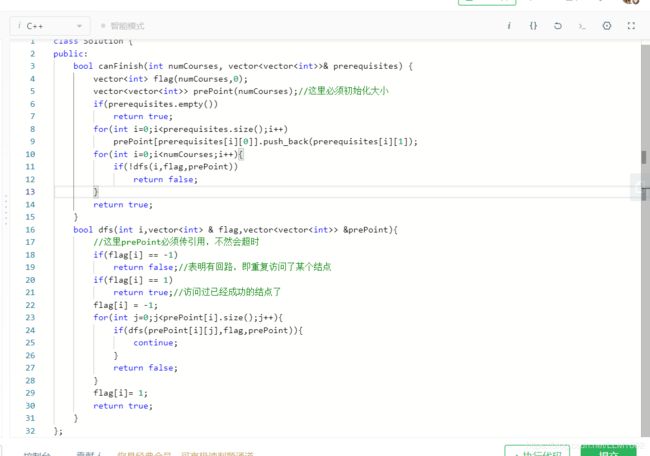
1：leetcode207(用dfs判断是否有环):https://leetcode-cn.com/problems/course-schedule/
思想：只要判断是否有环即可，有环则肯定不行。通过一个vector
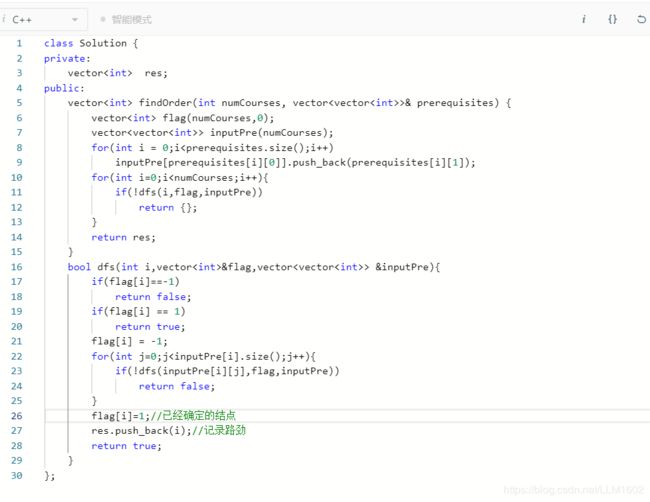
2：210（用dfs判断是否有环，同207）： https://leetcode-cn.com/problems/course-schedule-ii/
思想：如207，只是需要记录路径
代码：
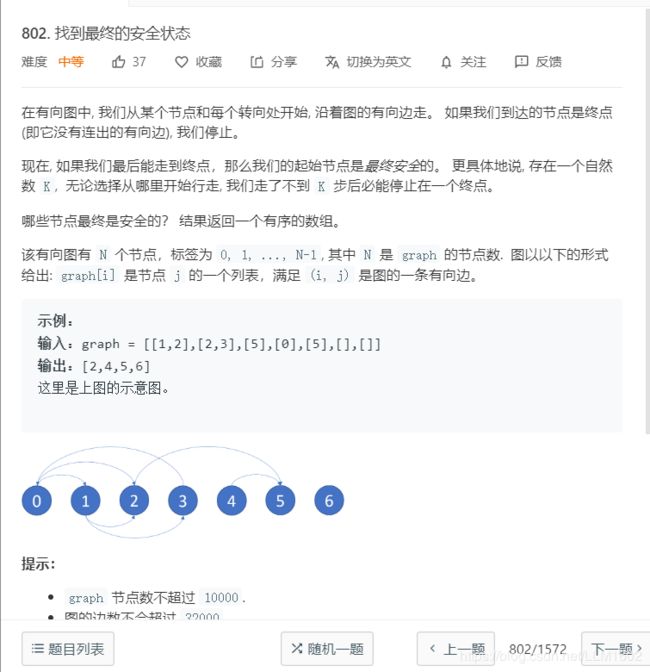
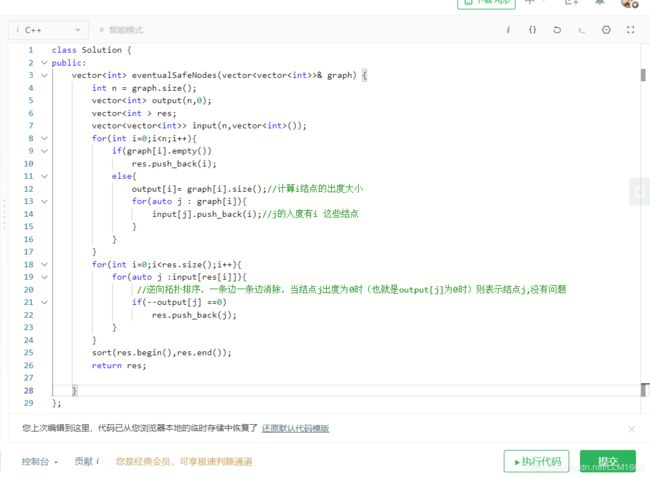
3：802（用拓扑排序来判断是否有环） https://leetcode-cn.com/problems/find-eventual-safe-states/
思想：就是判断从某个结点出发，如果不存在环，则加入结果集，此时不能再用207，210，那样的方法，会超时，这里选择拓扑排序，采用逆向的，也就是先将出度为0的结点加入结果集（出度为0，肯定是结果集的一员），再计算每个结点的出度output[i],再用input[i][j]来存储结点j->i的有向边，从结果集里选择出度为0的结点，比如i=1,结点1，去input[1][j]里找到，所有指向结点1的有向边，每遍历一条，就将结点j的出度，output[j]--,同时检出output[j]是否等与0，若output[j] ==0,则加入结果集。
代码：
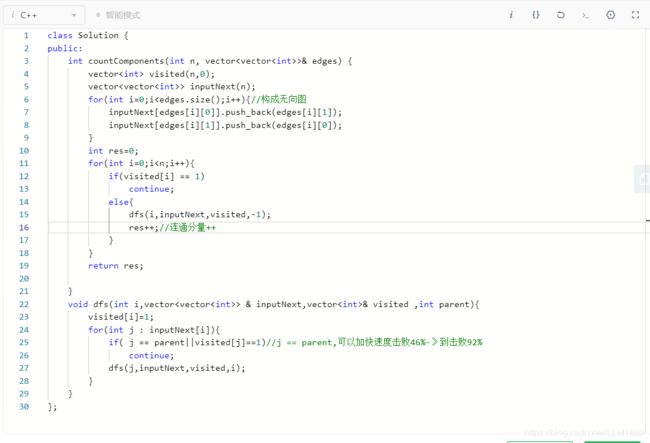
4：leetcode323（用dfs来数无向图连通分量个数）
https://leetcode-cn.com/problems/number-of-connected-components-in-an-undirected-graph/
思路：先构建无向图的邻接矩阵，再依此dfs,调用完一次dfs，无向图连通图的数量++，
代码：
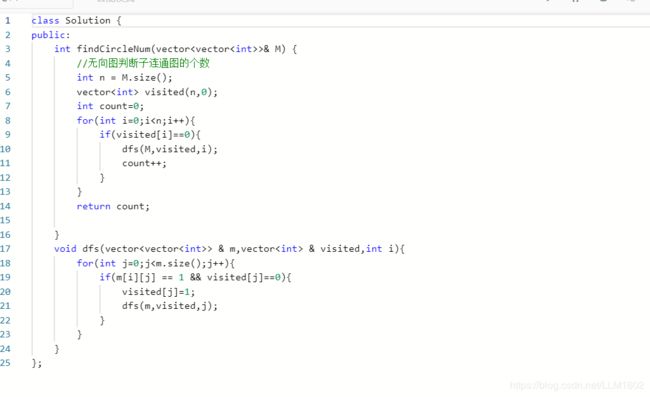
5：leetcode547(用dfs判断无向连通图的个数，同323，很相似)
https://leetcode-cn.com/problems/friend-circles/
代码：
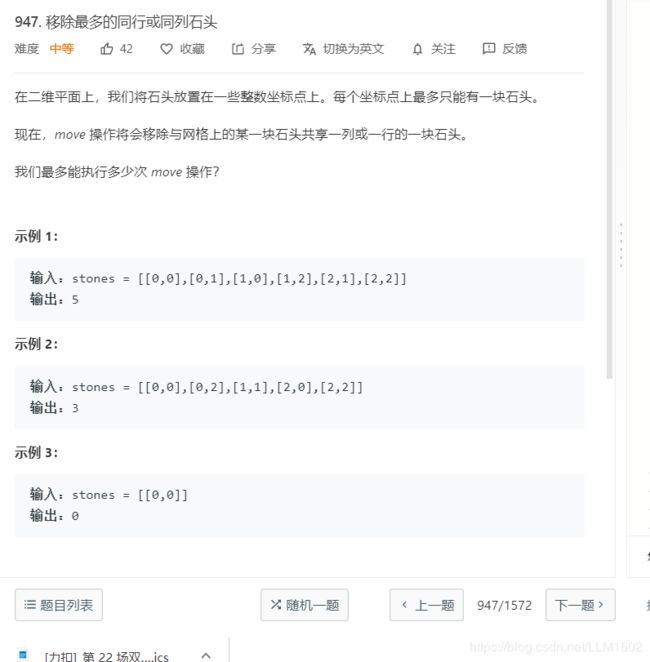
6：leetcode947(用并查集数无向连通图的个数)
https://leetcode-cn.com/problems/most-stones-removed-with-same-row-or-column/
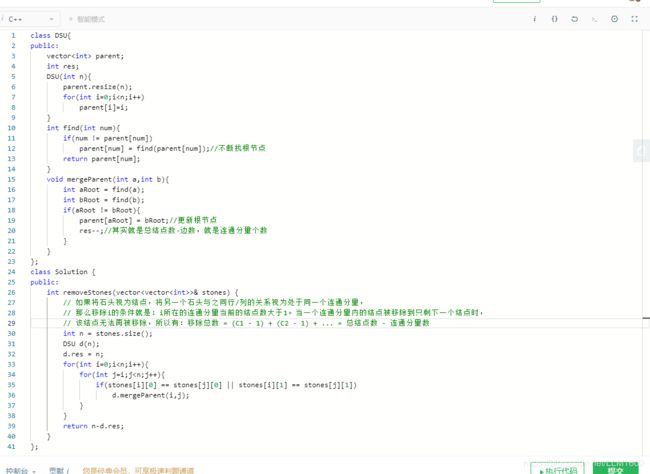
思路：将同一行的列，或行，就可看成无向连通图的边，通过不断更新根节点parent[i] = j，从而达到连起来的目的，记住并查集的模板，即建立一个class，DSU(){在parent[i] = i,(赋初值)},int find(){找根节点}，void merge(int a,int b){更新根节点}；
代码：
7：leetcode1319(同947,并查集解决无向图连通分量的个数)
https://leetcode-cn.com/problems/number-of-operations-to-make-network-connected/
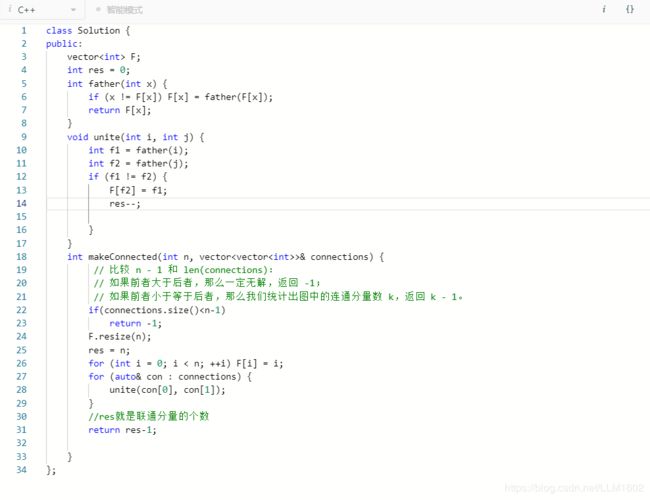
思路：首先要知道，要想整体连通，则变数 >= 结点数-1，然后就是计算连通分量个数，
代码：
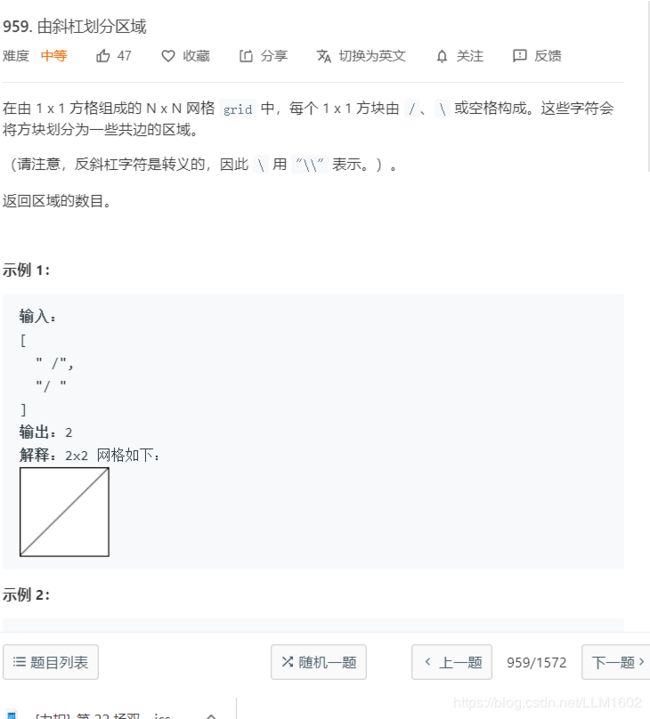
8:leetcode959（不同947和1319，仅仅是为了熟悉，记住并查集的模板才写在这，为了对比下，与dfs相似）
https://leetcode-cn.com/problems/regions-cut-by-slashes/
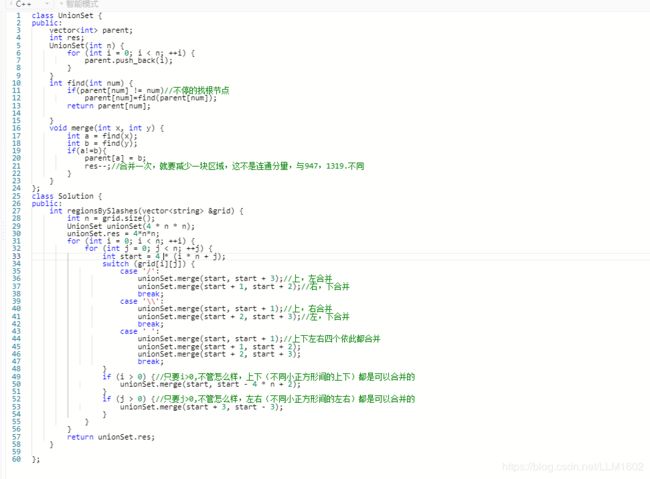
思想：把每个小正方形，分成上下左右四个更小的正方形
类似这样：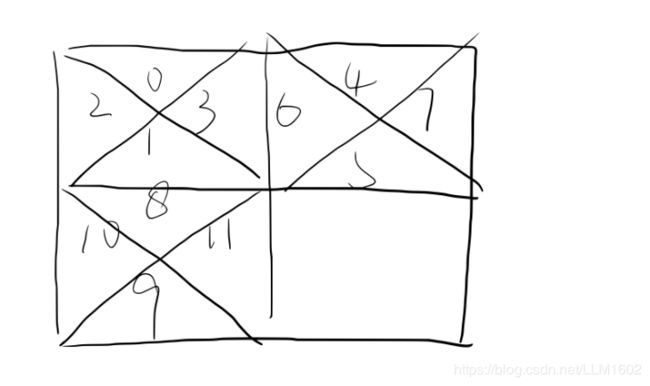
，初始结果为n*n*4,然后进行一小个一小个合并，每合并一次，结果--，
代码：
三：字符串型的dfs
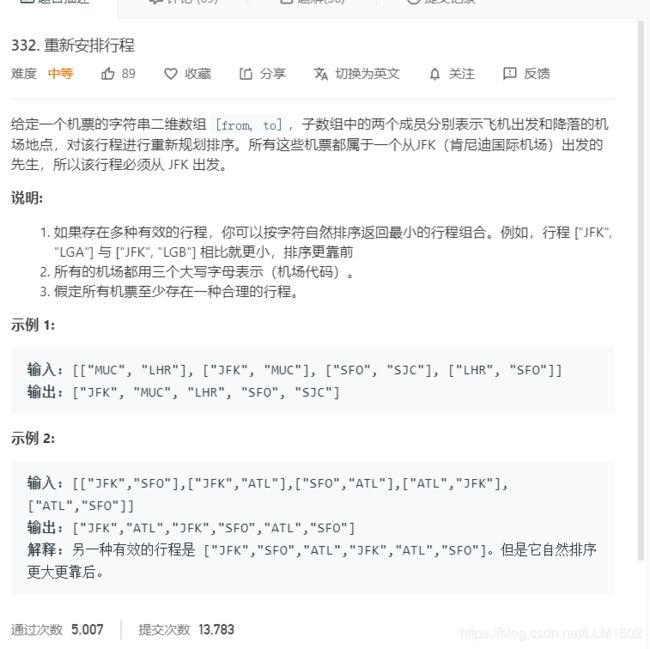
1:leetcode332(字符串转化为数字dfs)
https://leetcode-cn.com/problems/reconstruct-itinerary/
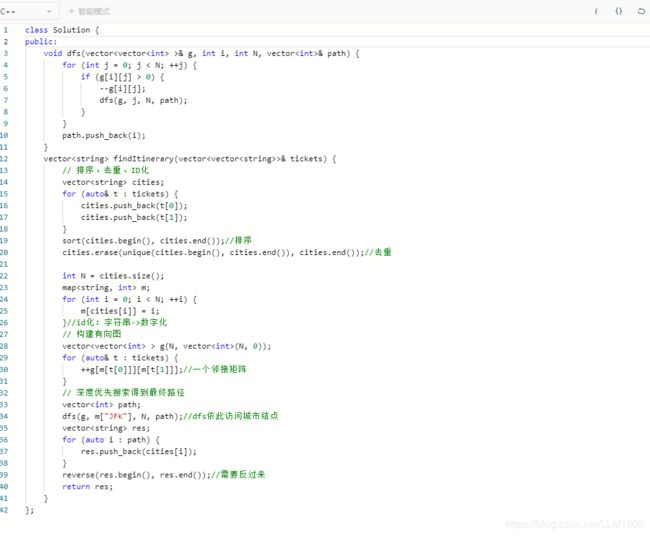
思想：其实就是一个连通图，已知起点，求按字母顺序的一个路径。将各城市转化为数字对应，建立邻接表，一遍dfs记录路径。
代码：
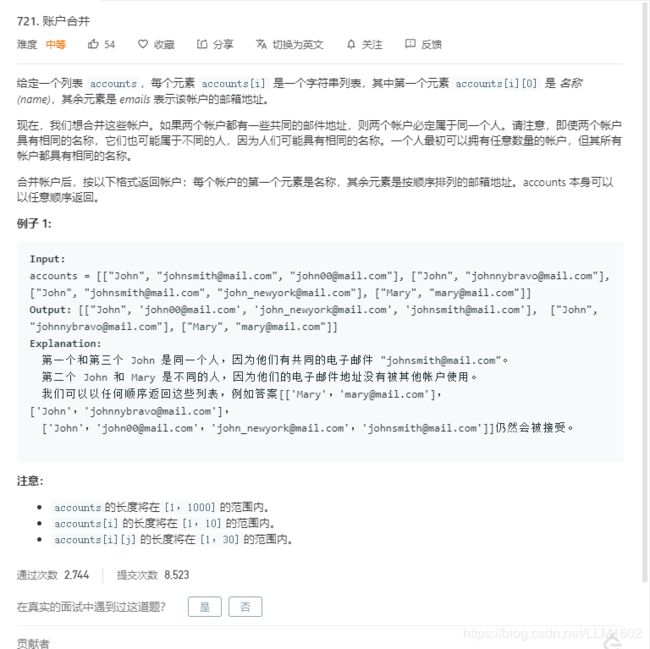
2：leetcode721
https://leetcode-cn.com/problems/accounts-merge/
题目：
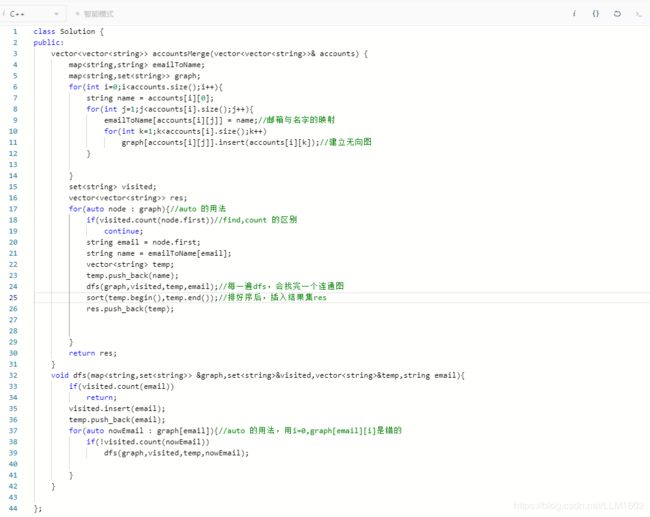
思想：以email来建立无向图，并建立一个email 到 name的映射，每一个Name,进行一次dfs,将与其相关的email的边连通起来，加入对应的结果集。
代码：
四：岛屿面积，数量，形状（上下左右）
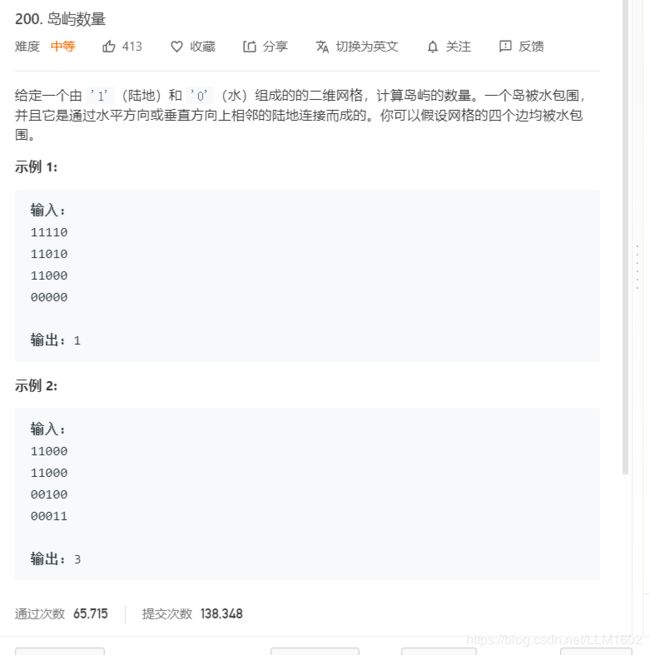
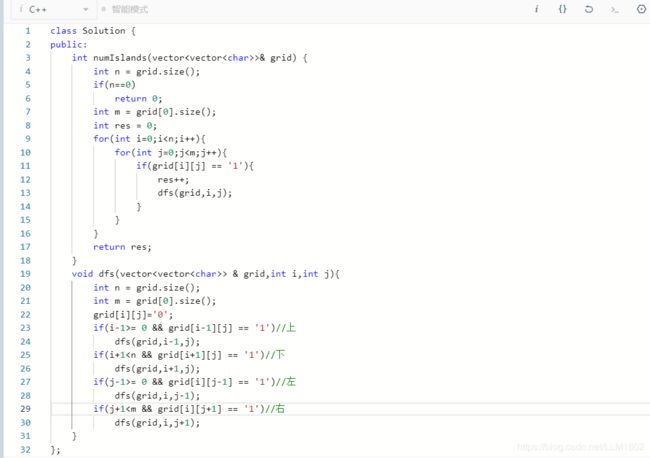
1：leetcode200(岛屿数量，就是计算连通分量个数，只不过在坐标上)
https://leetcode-cn.com/problems/number-of-islands/
思想：常规dfs，遇到1就继续上下左右一起扩张。
代码：
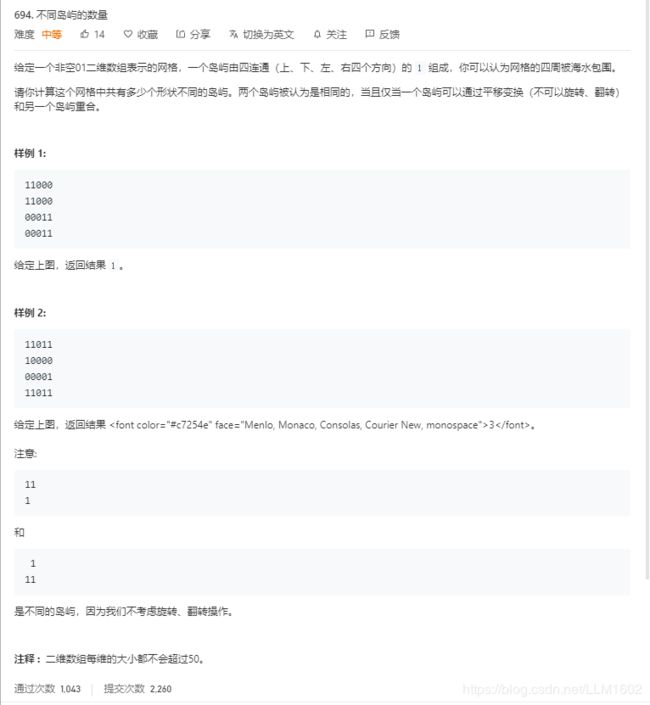
2：leetcode694(不同形状的岛屿数量)
https://leetcode-cn.com/problems/number-of-distinct-islands/
题目：
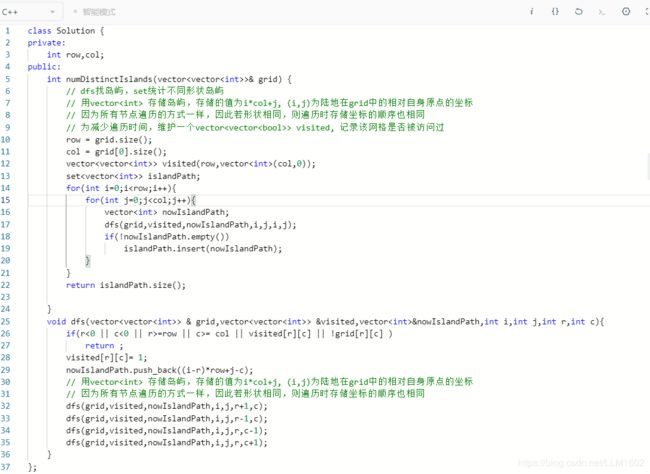
思想：其实与200题差不多，主要是如何理解形状，这里我们采用一个简单的方法，通过其所走的轨迹，来判断形状是否相同用set来存储，这样可以自动去重复的轨迹（也就是重复的轨迹并不会保存）。重点理解(i-r)*row+j-c。
代码：
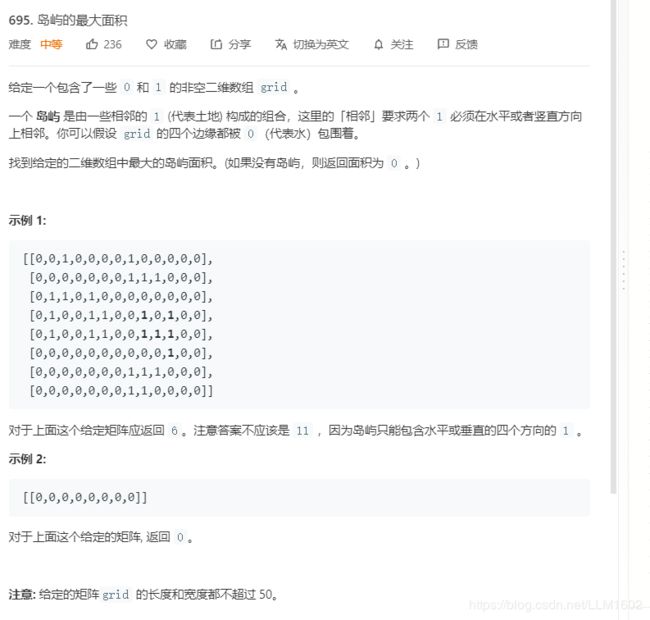
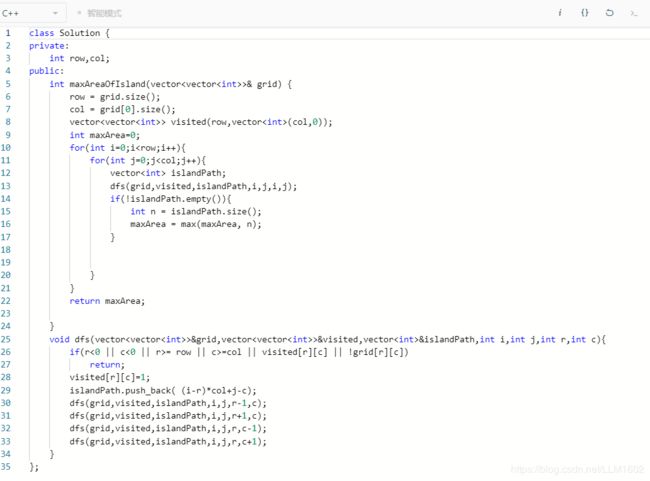
3：leetcode695(岛屿最大面积，其实同694不同形状的岛屿数量)
https://leetcode-cn.com/problems/max-area-of-island/
题目：
思想：只要求最大面积，则与694的不同形状，就很相似，只用不断更新最大路径的值即可。
代码：
五：迷宫，上下左右遍历
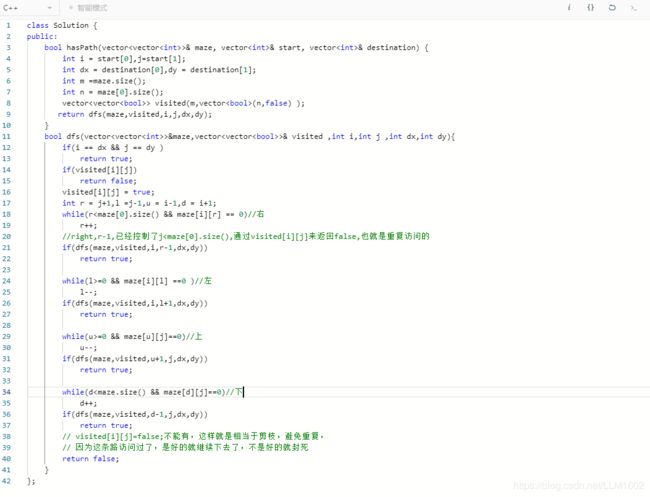
1：leetcode490
https://leetcode-cn.com/problems/the-maze/
思想：上下左右走，只不过要先用while来使其走到某个节点。
代码：
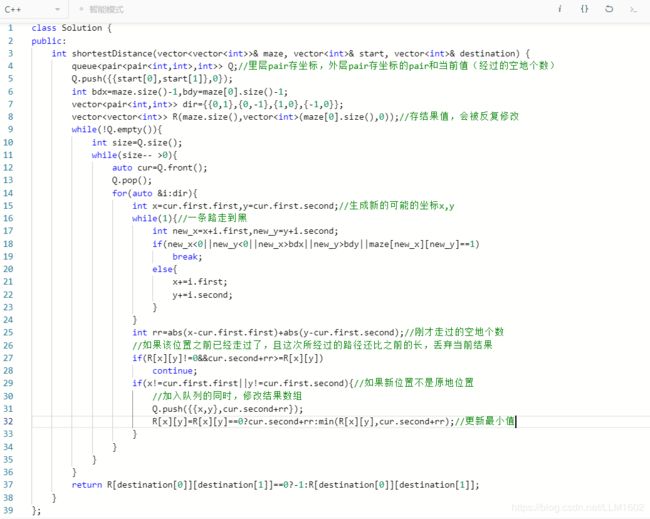
2：leetcode505(与490相似，只不过要求最短的路径)
https://leetcode-cn.com/problems/the-maze-ii/
题目：
思路：有点难，用BFS做，
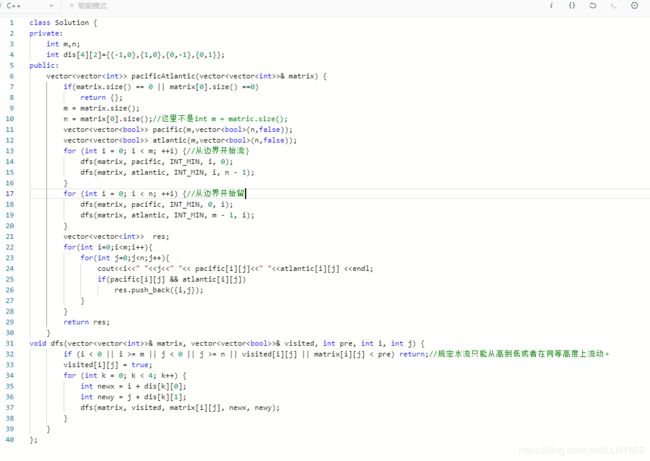
3：leetcode417(遍历方式改为从四周边界遍历)
https://leetcode-cn.com/problems/pacific-atlantic-water-flow/
题目：
思路：采用逆流的方法，因为能留到海洋，则当前位置的高度>=下一结点的高度，反过来，逆流，从海洋出发往里留，就是pre [i][j]<= now[i][j];
代码：
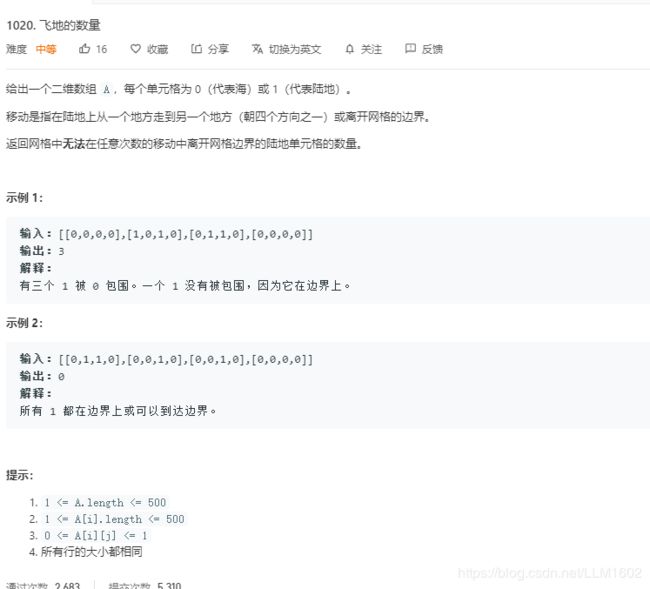
4：leetcode1020(依然从边界开始遍历)
https://leetcode-cn.com/problems/number-of-enclaves/
题目：
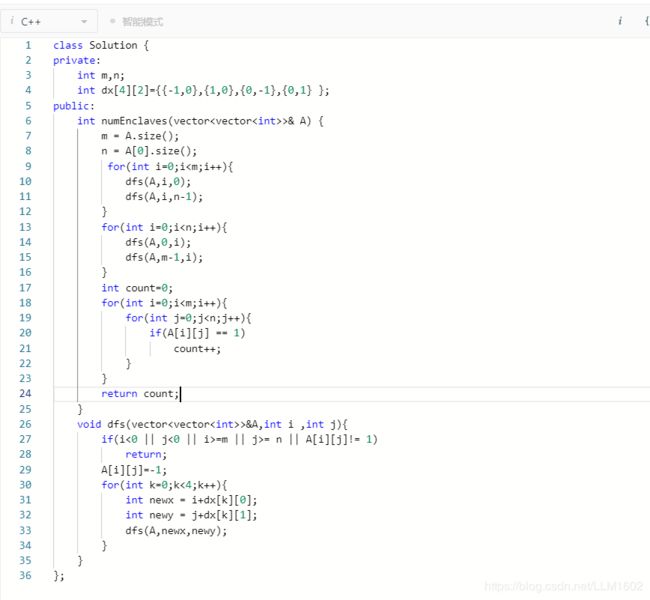
思路：要想算出不能走到边界上，那反过来想，就可以先算出来，可以从边界往里走，更改可以走到的值，最后再记录那些没有被更改的值的个数。
代码：
六：用dp解决的dfs
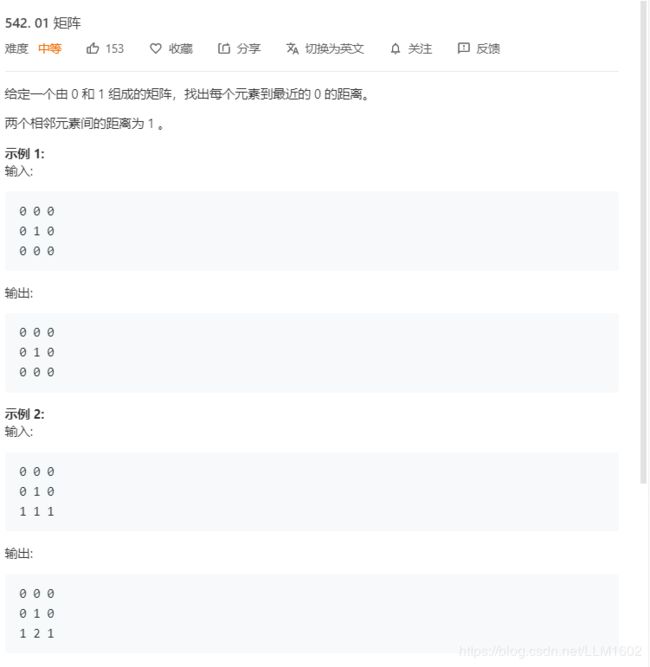
1:leetcode542
https://leetcode-cn.com/problems/01-matrix/
题目：
思路：
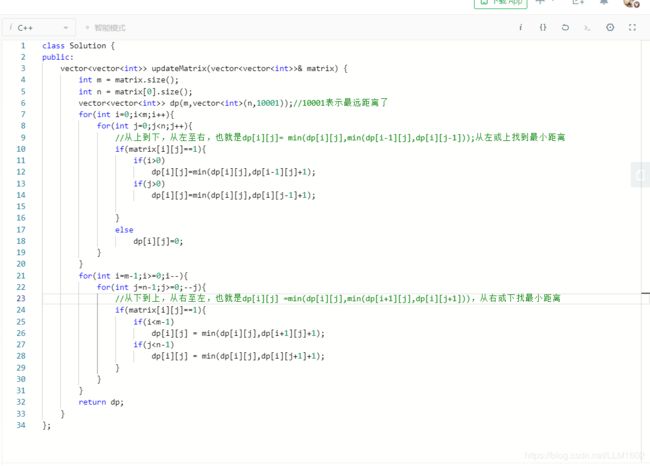
对于一个节点来说，它到 0 的距离可以通过邻居的最近距离计算，在这种情况下最近距离是邻居的距离 + 1。因此，这就让我们想到了动态规划！对于每个 1，到 0 的最短路径可能从任意方向。所以我们需要检查所有 4 个方向。在从上到下的迭代中，我们需要检查左边和上方的最短路径；我们还需要另一个从下往上的循环，检查右边和下方的方向。
从上至下、从左至右迭代整个矩阵
从下到上、从右至左迭代整个矩阵
代码：
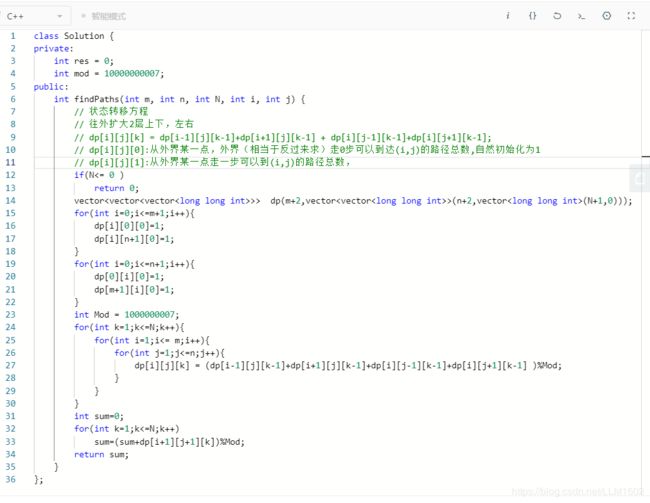
2：leetcode576(dp有点难)
https://leetcode-cn.com/problems/out-of-boundary-paths/
题目：
思想：
代码：
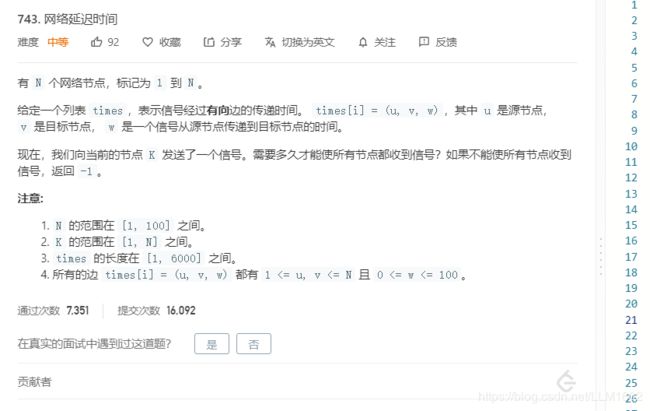
3：leetcode 743(在dfs的过程中，相当于加了个限制条件)
https://leetcode-cn.com/problems/network-delay-time/
题目：
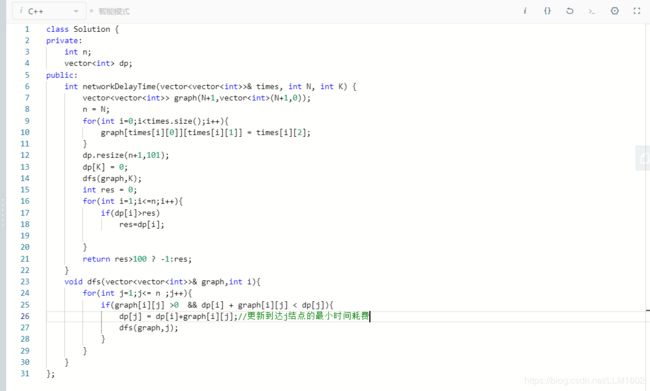
思想：有点像计算结点间的距离，要求最大距离，因此将每个结点的的dp[i] 计算，最后选取最大的，因为消息要传到每个人。
代码：
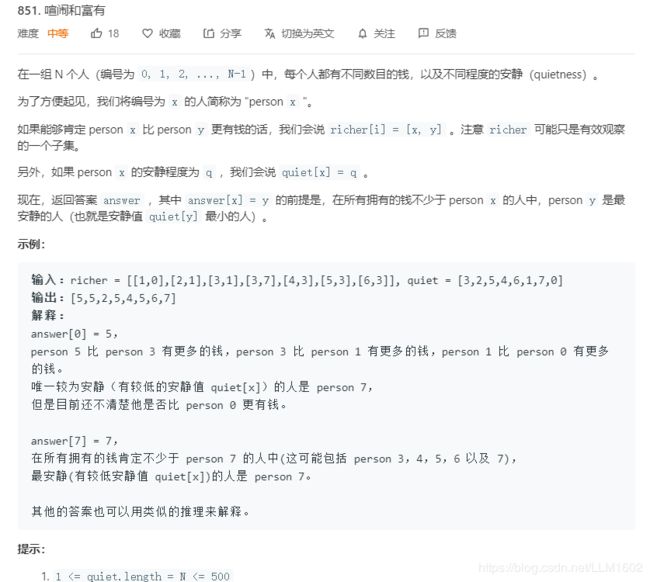
4:leetcode851()
https://leetcode-cn.com/problems/loud-and-rich/
题目：
思想：记忆化搜索，通过这种，已经确定了的状态来更快搜索。
代码：
