【leetcode笔记】数组
【leetcode笔记】数组
- 题数:13
- 知识点
- 1. 二/八/十六进制 前缀
- 2. unorder_map 的find()
- 3. 计算数组A的和 accumulate()
- 具体题目
- 1. 两数之和(E)
- 11. 盛最多水的容器(M)
- 15. 三数之和(M)
- 16. 最接近的三数之和(M)
- 26. 删除排序数组中的重复项(E)
- 27. 移除元素(E)
- 31. 下一个排列(M)
- 35. 搜索插入位置(E)
- 45. 跳跃游戏 II(H)
- 66. 加一
- 1010. 总持续时间可被 60 整除的歌曲(E)
- 1011. 在 D 天内送达包裹的能力(M)
- 1013. 将数组分成和相等的三个部分(E)
- 1275. 找出井字棋的获胜者(E)
题数:13
知识点
1. 二/八/十六进制 前缀
二进制以 0b 开头
八进制以 0 开头
十六进制以 0x 开头
2. unorder_map 的find()
if(map.find('B') == map.end()) //此时'B'不存在于map的键(key)中
3. 计算数组A的和 accumulate()
int sum = accumulate(A.begin(), A.end(), 0);
具体题目
1. 两数之和(E)
注意:
1.有暴力法,和用hash表查找两个方法
my version_1 code:
结果:AC
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
unordered_map<int,int> hash;
vector<int> re;
for (int i=0;i<nums.size();i++){
if(hash.find(target-nums[i])==hash.end()){
hash[nums[i]]=i;
}
else if(hash.find(target-nums[i])!=hash.end()){
re.push_back(hash[target-nums[i]]);
re.push_back(i);
}
}
return re;
}
};
灵感来源code:
class Solution
{
public:
vector<int> twoSum(vector<int> &nums, int target)
{
//Key是数字,value是该数字的index
unordered_map<int, int> hash;
vector<int> result;
int numsSize = int(nums.size());
for (int i = 0; i < numsSize; i++)
{
int numberToFind = target - nums[i];
//如果找到numberToFind,就return
if (hash.find(numberToFind) != hash.end())
{
result.push_back(hash[numberToFind]);
result.push_back(i);
return result;
}
//如果没有找到,把该数字的index放到hash表中
hash[nums[i]] = i;
}
return result;
}
};
11. 盛最多水的容器(M)
注意:
1.本题是一道经典的面试题,最优的做法是使用「双指针」。如果读者第一次看到这题,不一定能想出双指针的做法。
2.每次应该移动对应height数字较小的那个指针。
3.当两指针的height值相等时:假设随便移动一个,不管移动后的值比原值大还是小,总容积后不会比原来的值大。只能等到中间有两个比这个相等的数,更大的数才有可能比原值容积大。所以不管先移动哪里,或者同时移动都是可以的。
my version_1 code:
结果:超时;暴力两个for循环,可以预见的超时
class Solution {
public:
int maxArea(vector<int>& height) {
int max=0;
for (int i=0;i<(height.size()-1);i++){
for (int j=i+1;j<height.size();j++){
if (((j-i)*min(height[i],height[j]))>max){
max=(j-i)*min(height[i],height[j]);
}
}
}
return max;
}
};
my version_2 code:
结果:AC;超过97%;双指针
思路:参考了这道题 视频中 的官方解答-leetcode官方解答
class Solution {
public:
int maxArea(vector<int>& height) {
int left=0;
int right=height.size()-1;
int max=(right-left)*min(height[left],height[right]);
while(left!=right){
if (height[left]>=height[right]){
right--;
if (height[right]>height[right+1]){
if ((right-left)*min(height[left],height[right])>max){
max=(right-left)*min(height[left],height[right]);
}
}
}
if (height[left]<height[right]){
left++;
if (height[left]>height[left-1]){
if ((right-left)*min(height[left],height[right])>max){
max=(right-left)*min(height[left],height[right]);
}
}
}
}
return max;
}
};
15. 三数之和(M)
思路:
1.排序 + 双指针
本题的难点在于如何去除重复解。
2.算法流程:
1)特判,对于数组长度 n,如果数组为 null 或者数组长度小于 3,返回 []。
2)对数组进行排序。
3)遍历排序后数组:
- 若 nums[i]>0:因为已经排序好,所以后面不可能有三个数加和等于 0,直接返回结果。
- 对于重复元素:跳过,避免出现重复解
- 令左指针 L=i+1,右指针 R=n-1,当 L
-
- 当nums[i]+nums[L]+nums[R]==0,执行循环,判断左界和右界是否和下一位置重复,去除重复解。并同时将 L,R移到下一位置,寻找新的解
-
- 若和大于 0,说明 nums[R] 太大,R 左移
-
- 若和小于 0,说明 nums[L] 太小,L 右移
my version_1 code:
结果:AC;改了很久,比较乱
class Solution {
public:
vector<vector<int> > threeSum(vector<int>& nums) {
vector<vector<int> > re;
sort(nums.begin(), nums.end());
if (nums.size() < 3) return re;
int k = 0;
while (nums[k] <= 0 && k < nums.size() - 2) {
if (k > 0 && nums[k] == nums[k - 1]) { ///////////////
k += 1;
continue;
}
int i = k + 1;
int j = nums.size() - 1;
while (i < j) {
vector<int> temp;
if ((nums[k] + nums[i] + nums[j]) == 0) {
temp.push_back(nums[k]); temp.push_back(nums[i]); temp.push_back(nums[j]);
re.push_back(temp);
while (i < j && nums[i] == nums[i + 1]) {
i = i + 1;
}
while (i < j && nums[j] == nums[j - 1]) {
j = j - 1;
}
i = i + 1; j = j - 1;
}
else if ((nums[k] + nums[i] + nums[j]) > 0) {
j = j - 1;
}
else {
i = i + 1;
}
}
k = k + 1;
}
return re;
}
};
优秀思路code:
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
n=len(nums)
res=[]
if(not nums or n<3):
return []
nums.sort()
res=[]
for i in range(n):
if(nums[i]>0):
return res
if(i>0 and nums[i]==nums[i-1]):
continue
L=i+1
R=n-1
while(L<R):
if(nums[i]+nums[L]+nums[R]==0):
res.append([nums[i],nums[L],nums[R]])
while(L<R and nums[L]==nums[L+1]):
L=L+1
while(L<R and nums[R]==nums[R-1]):
R=R-1
L=L+1
R=R-1
elif(nums[i]+nums[L]+nums[R]>0):
R=R-1
else:
L=L+1
return res
16. 最接近的三数之和(M)
注意:
解题思路 双指针。类似于 第15题三数之和。
如果做过第15题,再做这一题会比较简单。
只需把原来的相加和为0,改成这里的target,再修改一下即可。
my version_1 code:
结果:AC
class Solution {
public:
int threeSumClosest(vector<int>& nums, int target) {
//主要步骤:先排序;最外一个大循环遍历元素;
//左指针k+1,右指针length-1;根据与target的比较移动指针
sort(nums.begin(),nums.end()); //排序
int SumClosest=nums[0]+nums[1]+nums[2]; //初始化三数之和
for(int k=0;k<(nums.size()-2);k++){
int i=k+1; //定义左指针
int j=nums.size()-1; //定义右指针
while(i<j){
//比较距离target的距离大小,更新SumClosest
int temp=abs(target-(nums[k]+nums[i]+nums[j]));
if(temp<abs(target-SumClosest)){
SumClosest=nums[k]+nums[i]+nums[j];
}
//比较和target的大小,移动左右指针
if((nums[k]+nums[i]+nums[j])>=target){
j=j-1;
}
else if((nums[k]+nums[i]+nums[j])<target){
i=i+1;
}
}
}
return SumClosest;
}
};
26. 删除排序数组中的重复项(E)
思路: 双指针法
数组完成排序后,我们可以放置两个指针 i 和 j,其中 i 是慢指针,而 j 是快指针。只要 nums[i] = nums[j],我们就增加 j 以跳过重复项。
当我们遇到 nums[i] != nums[j] 时,跳过重复项的运行已经结束,因此我们必须把它(nums[j])的值复制到 nums[i + 1]。然后递增 i.
接着我们将再次重复相同的过程,直到 jj 到达数组的末尾为止。
my version_1 code:
结果:AC; 超过80%左右
class Solution {
public:
int removeDuplicates(vector<int>& nums) {
int i=0;
if(nums.size()<1) return i;
for (int j=1;j<nums.size();j++){
if(nums[i]!=nums[j]){
//nums[++i]=nums[j]; //这里 ++i ,就相当于一条i=i+1语句
nums[i+1]=nums[j];
i=i+1;
}
}
return i+1;
}
};
27. 移除元素(E)
注意:
思路和做法 与第26题 很相似
my version_1 code:
结果:AC;超过70%左右
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
int i=0;
if(nums.size()<1) return i;
for(int j=0;j<nums.size();j++){
if(nums[j]!=val){
nums[i]=nums[j];
i++;
}
}
return i;
}
};
31. 下一个排列(M)
注意:
1.字典序的概念,要弄清楚
my version_1 code:
结果:AC;30%左右,很低。思路来自于官方解读。
官方解读
思路:
1)从后向前查找第一个相邻升序的元素对 (i,j),满足 A[i] < A[j]。此时 [j,end) 必然是降序
2)在 [j,end) 从后向前查找第一个满足 A[i] < A[k] 的 k。A[i]、A[k] 分别就是上文所说的「小数」、「大数」
3)将 A[i] 与 A[k] 交换
4)可以断定这时 [j,end) 必然是降序,逆置 [j,end),使其升序
5)如果在步骤 1 找不到符合的相邻元素对,说明当前 [begin,end) 为一个降序顺序,则直接跳到步骤 4
class Solution {
public:
void nextPermutation(vector<int>& nums) {
int i;
for(i=nums.size()-1;i>0;i--){
if(nums[i]>nums[i-1]) break;
}
int j;
if(i==0){ //这一段是为了防止nums完全倒序
int left=i;
int right=nums.size()-1;
while(left<right){
int temp;
temp=nums[left];
nums[left]=nums[right];
nums[right]=temp;
right--;
left++;
}
}
else{
for(j=nums.size()-1;j>i-1;j--){
if(nums[j]>nums[i-1]) break;
}
int tep;
tep=nums[i-1];
nums[i-1]=nums[j];
nums[j]=tep;
int left=i;
int right=nums.size()-1;
while(left<right){
int temp;
temp=nums[left];
nums[left]=nums[right];
nums[right]=temp;
right--;
left++;
}
}
}
};
my version_2 code:
结果:AC;80%左右;用上了两个C++ STL:swap() 交换 ; reverse() 求逆序
class Solution {
public:
void nextPermutation(vector<int>& nums) {
int i;
for(i=nums.size()-1;i>0;i--){
if(nums[i]>nums[i-1]) break;
}
if(i==0){ //这种情况,整个nums都是逆序
reverse(nums.begin(),nums.end());
}
else{
int j;
for(j=nums.size()-1;j>i-1;j--){
if(nums[j]>nums[i-1]) break;
}
swap(nums[j],nums[i-1]);
reverse(nums.begin()+i,nums.end());
}
}
};
优秀code:
思路一样,简洁优美
class Solution {
public:
void nextPermutation(vector<int>& nums) {
int pos = nums.size() - 1;
while (pos > 0 && nums[pos] <= nums[pos - 1])
pos--;
reverse(nums.begin() + pos, nums.end()); //逆序
if (pos > 0){
int start = pos;
for (; start < nums.size(); start++){ //寻找第一个大于nums[pos - 1]的数
if (nums[start] > nums[pos - 1]){
swap(nums[start], nums[pos - 1]); //交换
break;
}
}
}
}
};
v2:稍微改进下, 寻找第一个大于nums[pos - 1]的数原来为线性时间复杂度, 可以改用二分查找, 这里使用STL标准库upper_bound()
class Solution {
public:
void nextPermutation(vector<int>& nums) {
int pos = nums.size() - 1;
while (pos > 0 && nums[pos] <= nums[pos - 1])
pos--;
reverse(nums.begin() + pos, nums.end()); //逆序
if(pos > 0){
auto iter = upper_bound(nums.begin() + pos, nums.end(), nums[pos - 1]);//使用upper_bound找到遍历过的数中第一个比num[pos-1]大的数
swap(*iter, nums[pos - 1]);
}
}
};
35. 搜索插入位置(E)
注意:
思路:二分查找
my version_1 code:
结果:AC;超过95%
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int left=0;
int right=nums.size()-1;
int mid;
while(left<right){
mid=int((left+right)/2);
if(target<nums[mid]) right=mid-1;
if(target>nums[mid]) left=mid+1;
if(target==nums[mid]) return mid;
}
if(target>nums[left]) return left+1; //如果target比最后的还大,插入位置加1
return left;
}
};
45. 跳跃游戏 II(H)
注意:
1.感觉官方解读给出的算法,对于[10,9,8,7,6,5,3,2,1,1,0]这个测试用例求不出,感觉算法是错的
my version_1 code:
结果:WA;改不出来,灵感来自于官方解读。
主要是看跳到的第二层哪个能跳的更远,就选那个。
class Solution {
public:
int jump(vector<int>& nums) {
int edge = 0;
int cnt = 0;
while (edge < (nums.size()-1)) {
if ((edge+nums[edge])>=(nums.size()-1)){
cnt++;
break;
}
int max_jump = 0;
int step = 0;
int flag=0;
for (int i = 1; i <= nums[edge]; i++) {
if ((edge+nums[edge]+nums[edge+nums[edge]])>=(nums.size()-1)){
cnt++;
flag=1;
}
if (nums[edge + i] >= max_jump) {
max_jump = nums[edge + i];
step = i;
}
}
if (flag==1) break;
edge += step;
cnt++;
}
return cnt;
}
};
非常优秀的解题思路code:
思路:动态规划和贪心思想
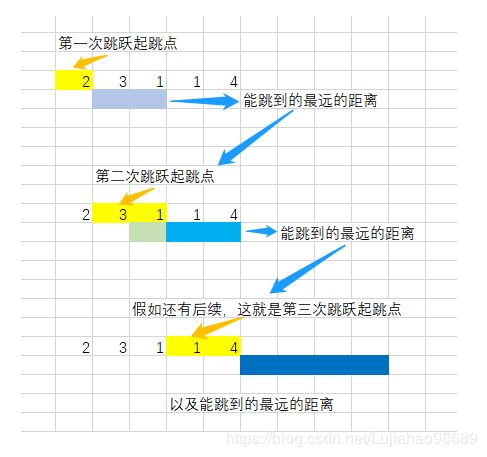
1.如果某一个作为 起跳点 的格子可以跳跃的距离是 3,那么表示后面 3 个格子都可以作为 起跳点。
(1)可以对每一个能作为 起跳点 的格子都尝试跳一次,把 能跳到最远的距离 不断更新。
2.如果从这个 起跳点 起跳叫做第 1 次 跳跃,那么从后面 3 个格子起跳 都 可以叫做第 2 次 跳跃。
3.所以,当一次 跳跃 结束时,从下一个格子开始,到现在 能跳到最远的距离,都 是下一次 跳跃 的 起跳点。
(1)对每一次 跳跃 用 for 循环来模拟。
(2)跳完一次之后,更新下一次 起跳点 的范围。
(3)在新的范围内跳,更新 能跳到最远的距离。
记录 跳跃 次数,如果跳到了终点,就得到了结果。
int jump(vector<int> &nums)
{
int ans = 0;
int start = 0;
int end = 1;
while (end < nums.size())
{
int maxPos = 0;
for (int i = start; i < end; i++)
{
// 能跳到最远的距离
maxPos = max(maxPos, i + nums[i]);
}
start = end; // 下一次起跳点范围开始的格子
end = maxPos + 1; // 下一次起跳点范围结束的格子
ans++; // 跳跃次数
}
return ans;
}
优化:
1)从上面代码观察发现,其实被 while 包含的 for 循环中,i 是从头跑到尾的。
2)只需要在一次 跳跃 完成时,更新下一次 能跳到最远的距离。
3)并以此刻作为时机来更新 跳跃 次数。
4)就可以在一次 for 循环中处理。
int jump(vector<int>& nums)
{
int ans = 0;
int end = 0;
int maxPos = 0;
for (int i = 0; i < nums.size() - 1; i++)
{
maxPos = max(nums[i] + i, maxPos);
if (i == end)
{
end = maxPos;
ans++;
}
}
return ans;
}
66. 加一
my version_1 code:
结果:AC;双一百


思路:
主要应用 递归 的方法实现,简洁明了。
- 一般情况:最后一位0-8
- 特殊情况:最后一位为9
1)可知最后一位变为0,并产生进位。删去最后一位,调用plusOne递归
2)若在数组中间部分出现一般情况,递归停止返回,递归出来一次,补一次之前删去的0
3)若数组是99…9类型,最前端原先的9,变成了10,然后递归停止,出来一次,补一次之前删去的0 - 返回结果
class Solution {
public:
vector<int> plusOne(vector<int>& digits) {
//一般情况,最后一位0-8,直接加1
if(digits.back()>=0 && digits.back()<=8){
digits.back() ++;
return digits;
}
//特殊情况,最后一位为9,需要进位
if(digits.back()==9){
digits.pop_back();
//其中,最特殊的情况是,都是99...9,这时需要在前面插入1位
if(digits.size()==0){
digits.push_back(1);
digits.push_back(0);
return digits;
}
plusOne(digits);
}
//递归结束,补足之前删去的0
digits.push_back(0);
return digits;
}
};
1010. 总持续时间可被 60 整除的歌曲(E)
注意:
1.先对编号进行离散化,因为除以60取余得到0-50之间的余数
2.然后利用排列组合,来得到答案
my version_1 code:
结果:超时
int num=0;
for (int i=0;i<(time.size()-1);i++){
for (int j=i+1;j<time.size();j++){
if ((time[i] + time[j]) % 60 == 0){
num++;
}
}
}
return num;
my version_2 code:
结果:通过
class Solution {
public:
int numPairsDivisibleBy60(vector<int>& time) {
int num=0;
vector<int> hash(60);
for(int i:time){
hash[i%60]++;
}
for(int j=0;j<31;j++){
if(j!=0 && j!=30){
num += (hash[j]*hash[60-j]);
}
if(j==0){
num += (hash[j]*(hash[j]-1))/2;
}
if(j==30){
num += (hash[j]*(hash[j]-1))/2;
}
}
return num;
}
};
优秀参考code:
class Solution {
public:
//2次遍历
int numPairsDivisibleBy60(vector<int>& time) {
int rs = 0;
vector<int>hash(60); //0-59
for (int num : time) {
hash[num%60]++;
}
//20 30 40
//1 2 2
for (int num : time) {
//遍历到一个数字 就让他-1,因为已经被用过了 比如20和40匹配 后面避免40和20匹配
int mod = num % 60;
hash[mod]--;
int target = mod == 0 ? 0 : 60 - mod;
rs += hash[target];
}
return rs;
}
//1次遍历
//天然有序了 因为从左向右遍历
int numPairsDivisibleBy60(vector<int>& time) {
int rs = 0;
vector<int>hash(60); //0-59
for (int num : time) {
int mod = num % 60;
//target -> 60-mod的下标 如果60-mod存在 则满足题意 +1
//如果 mod = 0 不能60-mod了 换成0 下次找0
int target = mod == 0 ? 0 : 60 - mod;
//当第一次遍历到30的时候,hash[30] = 0,当都二次遍历到30的时候,hash[30] = 1
//所以2个30,只被加了一次
rs += hash[target];
hash[mod]++;
}
return rs;
}
};
1011. 在 D 天内送达包裹的能力(M)
注意:
1.最低运载能力必然大于等于序列中的最大值;结果一定落在【max(weights), sum(weights)】这个区间之间
1)left 是单个货物的最大值(因为一艘船的最低运载能力是运送1个货物)
2)right是所有货物的总和,因为当一艘船的最大运载能力大于所有货物总和是,1天就完成所有货物运输,更大的运载能力是没有必要的;
2.要注意是在D天“内”完成,所有运载能力要尽量小,只要天数是在D天之内就可以
3.用二分算法查找
my version_1 code:
结果:AC;击败60%左右;第8次提交成功
class Solution {
public:
int shipWithinDays(vector<int>& weights, int D) {
//1.最低运载能力必然大于等于序列中的最大值;结果落在[max(weights), sum(weights)]
//2.要注意是在D天“内”完成,所以运载能力要尽量小,只要是在D天之内就可以
int left=*max_element(weights.begin(),weights.end());
int right=accumulate(weights.begin(),weights.end(),0);
int mid;
vector<int> re;
while(left<=right){
mid=int((left+right)/2); //去掉小数位取整
int temp=0;
int day=0;
for (int i=0;i<weights.size();i++){
temp += weights[i];
//当到某个包裹大于运载能力,之前的包裹记为一天
//这个包裹开始记为第二天
if (temp>mid){
day++;
temp=weights[i];
}
}
day++; //剩下的包裹再记一天
if (day>D){ //运载能力不够
left=mid+1;
}
if (day<=D){ //运载能力过剩
right=mid-1;
re.push_back(mid); //保存满足条件的运载能力数值
}
}
return *min_element(re.begin(),re.end()); //取其中的最小值返回
}
};
1013. 将数组分成和相等的三个部分(E)
注意:
my version_1 code:
结果:AC;击败10%左右,很低
思路:先把整个数组的和求出来,求平均,得到三个子数组的值;然后用迭代或者递归,一个个看里面有没有相加的平均值的子数组。有,返回true,没有,返回false
class Solution {
public:
bool canThreePartsEqualSum(vector<int>& A) {
int sum=0;
for (auto i:A){
sum=sum+i;
}
if ((sum%3)!=0) return false;
int ave=sum/3;
int temp_1=0;
int temp_2=0;
int temp_3=0;
for (int i=0;i<(A.size()-2);i++){
temp_1 += A[i];
if (temp_1==ave){
for (int j=i+1;j<(A.size()-1);j++){
temp_2 += A[j];
if (temp_2==ave){
for (int k=j+1;k<A.size();k++){
temp_3 += A[k];
if (temp_3==ave) return true;
}
return false;
}
}
return false;
}
}
return false;
}
};
简洁参考code:
解题思路:
1.首先计算数组 A中所有数字总和 sum
2.遍历数组 A查找和为 sum / 3的子数组个数
3.如果找到了三个这样的子数组则返回 true
4.找不到三个就返回 false
class Solution {
public:
bool canThreePartsEqualSum(vector<int>& A) {
int sum = accumulate(A.begin(), A.end(), 0);
if (sum % 3 != 0) {
return false;
}
int count = 0, subSum = 0;
for (int i = 0; i < A.size(); i ++) {
subSum += A[i];
if (subSum == sum / 3) {
count ++;
subSum = 0;
}
if (count == 3) {
return true;
}
}
return false;
}
};
双指针简洁版code:
class Solution {
public:
bool canThreePartsEqualSum(vector<int>& A) {
int sum=0,sum1=A[0],sum2=A[A.size()-1],left=1,right=A.size()-2;
for(int n:A) sum+=n; //计算数组总和
while(left<right && sum1!=sum/3) sum1+=A[left++];
while(right>0 && sum2!=sum/3) sum2+=A[right--];
return sum%3==0 & left<=right; //如果两个三分之一之间还存在元素,则为true
}
};
1275. 找出井字棋的获胜者(E)
注意:
1.所有游戏胜利的情况是 每行/每列 6种;交叉情况 2种。总共8种情况,可以遍历出这8种情况,来进行判断
my version_1 code:
结果:AC
class Solution {
int board[3][3]={{0,0,0},{0,0,0},{0,0,0}};
public:
string tictactoe(vector<vector<int>>& moves) {
int k=1;
int cnt=0;
for (auto i:moves){
board[i[0]][i[1]]=k;
if(check()){
if(k==1) return "A";
if(k==-1) return "B";
}
cnt++;
k=-k;
}
if(cnt<9) return "Pending";
return "Draw";
}
private:
bool check() {
return abs(board[0][0] + board[0][1] + board[0][2]) == 3 ||
abs(board[1][0] + board[1][1] + board[1][2]) == 3 ||
abs(board[2][0] + board[2][1] + board[2][2]) == 3 ||
abs(board[0][0] + board[1][0] + board[2][0]) == 3 ||
abs(board[0][1] + board[1][1] + board[2][1]) == 3 ||
abs(board[0][2] + board[1][2] + board[2][2]) == 3 ||
abs(board[0][0] + board[1][1] + board[2][2]) == 3 ||
abs(board[2][0] + board[1][1] + board[0][2]) == 3;
}
};
优秀参考code:(正常思维)
class Solution {
private:
int board[3][3] = {{0, 0, 0}, {0, 0, 0}, {0, 0, 0}};
bool check() {
return abs(board[0][0] + board[0][1] + board[0][2]) == 3 ||
abs(board[1][0] + board[1][1] + board[1][2]) == 3 ||
abs(board[2][0] + board[2][1] + board[2][2]) == 3 ||
abs(board[0][0] + board[1][0] + board[2][0]) == 3 ||
abs(board[0][1] + board[1][1] + board[2][1]) == 3 ||
abs(board[0][2] + board[1][2] + board[2][2]) == 3 ||
abs(board[0][0] + board[1][1] + board[2][2]) == 3 ||
abs(board[2][0] + board[1][1] + board[0][2]) == 3;
}
public:
string tictactoe(vector<vector<int>>& moves) {
int piece = 1;
for (auto move: moves) {
board[move[0]][move[1]] = piece;
if (check())
return piece > 0 ? "A" : "B";
piece = -piece;
}
return moves.size() < 9 ? "Pending" : "Draw";
}
};
优秀参考code:(位运算)
用位运算处理比较简洁。棋盘可以用二进制编码成9位,整个棋盘只有8种胜利条件(三纵三横两个对角线)。
这三种局势可编码为:
int a = 0b100100100;
int b = 0b010010010;
int c = 0b001001001;
int d = 0b111000000;
int e = 0b000111000;
int f = 0b000000111;
int g = 0b100010001;
int h = 0b001010100;
同时分别用两个变量保存棋手A和B的落子情况。
并且每次落子之后,遍历是上面8个胜利条件,只要有一个满足就算胜。
其中,落子通过位或运算,判断胜利通过位与运算。
落子的位置是将0b1向左移(2 - x) * 3 + (2 - y) = 8 - 3 * x - y位。
判断胜利(例如局面a)条件为((落子&a)==a)。
class Solution {
public:
int correct_mask[8] = {0b100100100, 0b010010010, 0b001001001, 0b111000000,
0b000111000, 0b000000111, 0b100010001, 0b001010100};
string tictactoe(vector<vector<int>>& moves) {
int counter = 0;
int map_A = 0x000000000;
int map_B = 0x000000000;
for (auto step = moves.begin(); step != moves.end(); ++step){
int x = (*step)[0];
int y = (*step)[1];
int shift = 8 - 3 * x - y;
if (counter % 2 == 0){ // for playerA
map_A = map_A | (0b1<<shift);
}else{ // for playerB
map_B = map_B | (0b1<<shift);
}
// check wins
for (int i = 0; i < 8; ++i){
if ((map_A & correct_mask[i]) == correct_mask[i]){
return "A";
}else if((map_B & correct_mask[i]) == correct_mask[i]){
return "B";
}
}
counter += 1;
}
if (counter == 9){
return "Draw";
}else{
return "Pending";
}
}
};