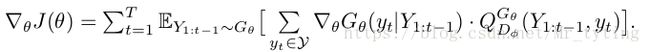论文分享-- >SeqGAN: Sequence Generative Adversarial Nets with Policy Gradient

博客内容将首发在微信公众号"跟我一起读论文啦啦"，上面会定期分享机器学习、深度学习、数据挖掘、自然语言处理等高质量论文，欢迎关注！

本次要分享和总结的论文为：$SeqGAN:SequenceGenerativeAdversarialNetswithPolicyGradient$，其论文链接SeqGAN，源自$AAAI-17$，参考的实现代码链接代码实现。

本篇论文结合了$GAN$ 和$RL$ 的知识，整篇论文读下来难度较大，在这里就浅薄的谈下自己的见解。

好了，老规矩，带着代码分析论文。

动机

• 我们知道$GAN$ 网络在计算机视觉上得到了很好的应用，然而很可惜的是，其在自然语言处理上并不$work$，最初的 $GANs$ 仅仅定义在实数领域，$GANs$ 通过训练出的生成器来产生合成数据，然后在合成数据上运行判别器，判别器的输出梯度将会告诉你，如何通过略微改变合成数据而使其更加现实。一般来说只有在数据连续的情况下，你才可以略微改变合成的数据，而如果数据是离散的，则不能简单的通过改变合成数据。例如，如果你输出了一张图片，其像素值是$1.0$，那么接下来你可以将这个值改为$1.0001$。如果输出了一个单词“penguin”，那么接下来就不能将其改变为“penguin + .001”，因为没有“penguin +.001”这个单词。 因为所有的自然语言处理（$NLP$）的基础都是离散值，如“单词”、“字母”或者“音节”， $NLP$ 中应用 $GANs$ 是非常困难的。
• $GAN$ 只能衡量一个完整的句子的好坏程度，对于部分生成的句子，很难预测其后面的部分，无法很好的对其打分。
• 在传统的$seq2seq$ 模型中，我们通常用$maxlikelihood$ 来训练模型，但是这个训练方式也存在一个严重的问题，也就是论文中所说的$exposurebias$ ，在模型训练阶段，我们用$truetokens$ 作为 $decoder\_input$，但是在真正的预测阶段时，我们只能从上一步产生的分布中以某种方式抽样某一个$token$ 作为下一步的$decoder\_input$，也就是这个阶段的$deocder\_input$ 的分布可能是不一样的。

论文的大体思路

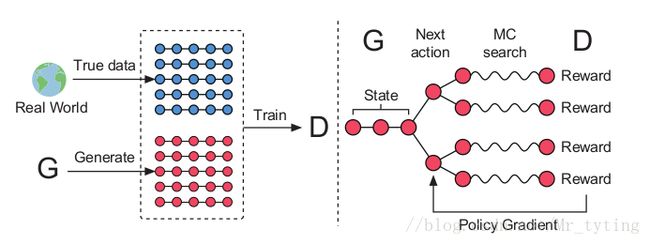
我们先看左图：现在有一批$true\_data$，生成器生成一批假数据，我们利用$MLE$ 的方式来$pretrain$ 生成器，也就是让生成器不断拟合$true\_data$ 的分布。这个过程经过几个回合；然后把训练好的生成器生成的数据作为$negtive\_data$，$True\_data$ 作为$positive\_data$ 来$pretrain$ 判别器。 这样就$pretrain$ 出了生成器和判别器。

再看右图：先了解下强化学习的四个重要概率：$state,action,policy,reward$，$state$ 为现在已经生成的$tokens$ , $action$是下一个即将生成的$token$ , $policy$ 为$GAN$ 的生成器，$reward$ 为$GAN$ 的判别器所回传的信息。

带着代码仔细分析各个部分

在实现代码中，生成器是一个$LSTM$ 神经网络，判别器是一个$CNN$ 网络，其$true\_data$ 是由一个$target\_LSTM$ 生成的。

pretrain

由上面的分析可知，在$pretrain$ 生成器时，只是利用$MLE$ 的方法来训练，不需要考虑$reward$。

我们先看看代码中是如何$pretain$ 生成器的：

for epoch in xrange(PRE_EPOCH_NUM):
	## gen_data_loader存储真实数据。
    loss = pre_train_epoch(sess, generator, gen_data_loader)##该操作为利用MLE训练生成器
    if epoch % 5 == 0:
    ┆   generate_samples(sess, generator, BATCH_SIZE, generated_num, eval_file)## 利用生成器生成一批假数据
    ┆   likelihood_data_loader.create_batches(eval_file)##将假数据存进likelihood_data_loader
    ┆   test_loss = target_loss(sess, target_lstm, likelihood_data_loader)##测试下当前生成的假数据与target_lstm生成的真实数据的loss
    ┆   print 'pre-train epoch ', epoch, 'test_loss ', test_loss
    ┆   buffer = 'epoch:\t'+ str(epoch) + '\tnll:\t' + str(test_loss) + '\n'
    ┆   log.write(buffer)

以上过程循环$PRE\_EPOCH\_NUM$ 个循环，不断的$pretrain$ 生成器。

再来看看怎么$pretrain$ 判别器的：

for _ in range(50):
    generate_samples(sess, generator, BATCH_SIZE, generated_num, negative_file)##上面的生成器生成一批负样本
    dis_data_loader.load_train_data(positive_file, negative_file)
    for _ in range(3):
    ┆   dis_data_loader.reset_pointer()
    ┆   for it in xrange(dis_data_loader.num_batch):
    ┆   ┆   x_batch, y_batch = dis_data_loader.next_batch()##获取一个batch数据,二分类
    ┆   ┆   feed = {
    ┆   ┆   ┆   discriminator.input_x: x_batch,
    ┆   ┆   ┆   discriminator.input_y: y_batch,
    ┆   ┆   ┆   discriminator.dropout_keep_prob: dis_dropout_keep_prob
    ┆   ┆   }
		    ## 判别器是一个二分类的CNN网络，利用cross-entropy作为损失函数。
    ┆   ┆   _ = sess.run(discriminator.train_op, feed)##训练判别器

生成器的目标函数

由强化学习的相关知识，我们可知其目标就是$maximizeexpectedendreward$，也就是生成器生成了一句完整的句子后，我们希望尽可能的使其所有$tokens$ 的$reward$ 之和尽可能的大，也就是如何公式：
$$J(\theta )=E[R_T|S_0,\theta ]=\sum _{y1\in Y}{G}_{\theta }(y_1|s_0)\ast Q_{D_{\varphi }}^{G_{\theta }}(s_0,y_1)$$

如何理解上式呢？其中$R_T$ 可理解为一个完整句子的$reward$ 之和，$s_0$ 表示初始状态，$\theta$ 表示生成器的参数。后面的求和过程表示，每生成一个$token$，我们都会计算其生成该$token$ 的概率与其对应的$reward$ 值，那么两者相乘即表示生成该$token$ 的期望$reward$ 值。求和后即为该整句的期望$reward$ 值。生成器的目标就是不断的$maximizeJ(\theta )$。 至于$reward$ 为啥表示成$Q_{D_{\varphi }}^{G_{\theta }}$，因为$reward$ 是由后面判别器$D_{\varphi }$ 决定的。

reward 求法

由上面的$J(\theta )$ ，如何求每一步的$reward$ 呢？也就是求$D_{\varphi }$。论文中提到$GAN$ 只能对一个完整的句子进行打分，而不能对生成的不完整句子打分，因此引入强化学习的方式：
$$Q_{D_{\varphi }}^{G_{\theta }}(\alpha =y_t,s=Y_{1:T-1})=Q_{D_{\varphi }}(Y_{1:T})$$

蒙特卡洛树搜索方法：

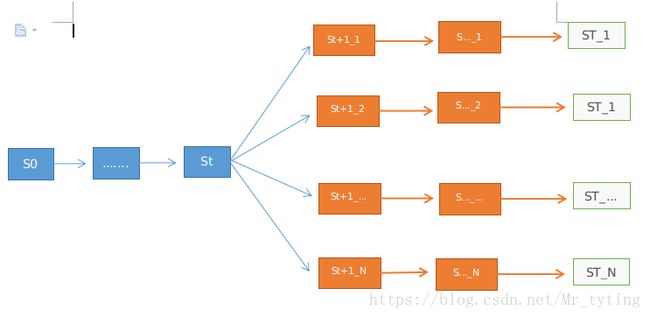
在$train$ 的阶段时，我们希望生成器生成的$token$ 在当前生成概率分布中对应的概率与该$token$ 的$reward$ 乘积和越大越好（上面的$J(\theta )$意义），那么该$token$ 的$reward$ 如何计算得到呢？要知道只有是一个完整的句子，其判别器才能对其进行打分。例如我们在生成第$t$ 步的$token$时，后面的$tokens$ 是未知的，我们只能让生成器继续向后面生成$token$，直到生成一个完整的句子。然后在喂给判别器打分，为了让这个打分更有说服力，我们让这个过程重复$N$ 次，然后取平均的$reward$，可以用如下图示展示这个过程：

简单来说，就是生成器每生成一个$token$ 都会有相应的一个$reward$，而这个$token$ 后面的$tokens$ 都是未知的，只能按照生成器来补全，形成一个完整的句子，这个过程进行$N$ 次，会生成$N$ 个不同的完整句子(因为生成器的随机性，不可能出现相同的句子)。然后将这$N$个句子放到判别器中得到$N$ 个不同的打分结果，对这$N$ 个打分结果取平均作为该$token$ 最终的$reward$，论文中讲到当生成第$t$ 个$token$ 时：
$$\{Y_{1:T}^1,....,Y_{1:T}^N\}=M{C}^{G_{\beta }}(Y_{1:t};N)$$

上式左边表示$sample$ 出来的 $N$ 个不同的完整句子。

综上所述：
$$Q_{D_{\varphi }}^{G_{\theta }}(\alpha =y_t,s=Y_{1:T-1})=\{\begin{array}{cc}\frac{1}{N}{\sum }_{n=1}^N{D}_{\varphi }(Y_{1:T}^n),Y_{1:T}^n\in M{C}^{G_{\beta }}(Y_{1:t};N)& fort<T\\ D_{\varphi }(Y_{1:t})& fort=T\end{array}$$

那么代码中是如何实现这一步的呢？

def get_reward(self, sess, input_x, rollout_num, discriminator):
"""
input_x: 需要打分的序列
rollout_num: 即sample的次数，即上面的N
discriminator: 判别器
"""
    rewards = []
    for i in range(rollout_num):
    ┆   # given_num between 1 to sequence_length - 1 for a part completed sentence
		会遍历一整句中的每个token,给其打分
    ┆   for given_num in range(1, self.sequence_length ):
    ┆   ┆   feed = {self.x: input_x, self.given_num: given_num}
		    ##生成一批样本，前give_num的token由input_x提供，give_num后的token由生成器补上。由此生成一批完整的句子。
    ┆   ┆   samples = sess.run(self.gen_x, feed)
    ┆   ┆   feed = {discriminator.input_x: samples, discriminator.dropout_keep_prob: 1.0}
    ┆   ┆   ypred_for_auc = sess.run(discriminator.ypred_for_auc, feed)##喂给判别器，给每个句子打分，作为reward
    ┆   ┆   ypred = np.array([item[1] for item in ypred_for_auc])
    ┆   ┆   if i == 0:
    ┆   ┆   ┆   rewards.append(ypred)
    ┆   ┆   else:
    ┆   ┆   ┆   rewards[given_num - 1] += ypred## 在rollout_num循环中，相同位置的reward相加。

    ┆   # the last token reward
    ┆   feed = {discriminator.input_x: input_x, discriminator.dropout_keep_prob: 1.0}##如果give_num已经是最后一个token了，则喂给判别器的样本就全是input_x。
    ┆   ypred_for_auc = sess.run(discriminator.ypred_for_auc, feed)
	    ##注意下：ypred_for_auc只是softmax_logits,二分类的，第一个数为该样本为假样本概率，第二个数为其为真样本概率
    ┆   ypred = np.array([item[1] for item in ypred_for_auc])##我们拿其真样本概率作为reward
    ┆   if i == 0:
    ┆   ┆   rewards.append(ypred)
    ┆   else:
    ┆   ┆   # completed sentence reward
    ┆   ┆   rewards[self.sequence_length - 1] += ypred

    rewards = np.transpose(np.array(rewards)) / (1.0 * rollout_num)  # batch_size x seq_length##取平均值。
    return rewards

通过上面的分析，我们可知，每个$token$ 的$reward$ 都是由判别器得到的。那么这个打分的过程是怎么做的呢？我们来看看判别器的实现代码：

不行，代码太多了，简单解说：生成器就是一个$CNN$ 网络，我们会将$input\_x$ (二分类的) $reshape$ 成一个四维的张量，然后通过各种的卷积，$pooling$ 操作得到一个结果，然后再经过一个线性操作最终得到只有二维的张量，再做一个$softmax$ 操作得到$ypred$ 作为$reward$ 值等等，直接看下面精华代码：

with tf.name_scope("output"):##num_classes为2，真样本还是假样本
    W = tf.Variable(tf.truncated_normal([num_filters_total, num_classes], stddev=0.1), name="W")
    b = tf.Variable(tf.constant(0.1, shape=[num_classes]), name="b")
    l2_loss += tf.nn.l2_loss(W)
    l2_loss += tf.nn.l2_loss(b)
    self.scores = tf.nn.xw_plus_b(self.h_drop, W, b, name="scores")
    self.ypred_for_auc = tf.nn.softmax(self.scores)##reward
    self.predictions = tf.argmax(self.scores, 1, name="predictions")

# CalculateMean cross-entropy loss
with tf.name_scope("loss"):
    losses = tf.nn.softmax_cross_entropy_with_logits(logits=self.scores, labels=self.input_y)
    self.loss = tf.reduce_mean(losses) + l2_reg_lambda * l2_loss

***其实就是将该整句被判别器判别为真样本的概率作为该 $token$ 的 $reward$***，嗯，就是这么简单。判别为真样本的概率越大，则在当前步选择该$token$ 越正向。

值得一提的是：这里$reward$ 的方式并不唯一，论文中的对比实验就用了$blue$ 指标作为$reward$ 来指导生成器的训练。

好了，怎么求$reward$ 已经搞清楚了。

接下来再看看判别器是如何训练的？以及他的目标函数。

判别器的目标函数

简短解说：判别器是一个$CNN$ 网络，我们喂给判别器的样本是一个二分类的样本，即有生成器生成的一批假样本，也有一批真样本，然后直接做个二分类，损失函数就是一个$cross\_entropy$ :
$$\underset{\varphi }{\min }-E_{Y\sim p_{data}}\left[log{D}_{\varphi }(Y)\right]-E_{Y\sim G_{\theta }}\left[log(1-D_{\varphi }(Y))\right]$$

实现代码上面已写到。

policy Gradient

这一步有大量的数学公式需要推导。

我们由上面的分析，知道生成器的目标函数为：
$$J(\theta )=E[R_T|S_0,\theta ]=\sum _{y_1\in Y}{G}_{\theta }(y_1|s_0)\ast Q_{D_{\varphi }}^{G_{\theta }}(s_0,y_1)$$

我们再来看看上式是如何得到的：
$$Q^{G_{\theta }}(s=Y_{1:t-1},\alpha =y_t)=V^{G_{\theta }}(Y_{1:t})$$

可以这么理解：上式在$G_{\theta }$ 为生成器时，状态为已经生成$1$ 到$(t-1)$ 的$tokens$ 情况下，当前第$t$ 步选择$\alpha$ 的$reward$ 值。那么：
$$V^{G_{\theta }}(s=Y_{1:t-1})=\sum _{y_t\in Y}{G}_{\theta }(y_t|Y_{1:t-1})\ast Q^{G_{\theta }}(Y_{1:t-1},y_t)=\sum _{y_t\in Y}{G}_{\theta }(y_t|Y_{1:t-1})\ast V^{G_{\theta }}(Y_{1:t})$$

这样，一个完整句子的期望$reward$ 就可以表示成$$J(\theta )=E[R_T|S_0,\theta ]=\sum _{y_1\in Y}{G}_{\theta }(y_1|s_0)\ast Q_{D_{\varphi }}^{G_{\theta }}(s_0,y_1)$$
那么如何$maximizeJ(\theta )$ 呢？利用$gradientascend$ 方法，需要对$\theta$ 求导。

具体求导过程就不赘述了，如有兴趣请看论文。

最后求出的结果为：

利用梯度上升法来更新生成器参数：
$$\theta =\theta +{\alpha }_h{▽}_{\theta }J(\theta )$$

那么目标函数的优化过程在代码中如何实现呢？

self.g_loss = -tf.reduce_sum(
	## self.x 为生成器生成一个序列,我们需要找到这个序列中每个token在生成器分布中的概率，然后与对应的reward相乘。求和取负作为要优化的loss
    tf.reduce_sum(
    ┆   tf.one_hot(tf.to_int32(tf.reshape(self.x, [-1])), self.num_emb, 1.0, 0.0) * tf.log(
    ┆   ┆   tf.clip_by_value(tf.reshape(self.g_predictions, [-1, self.num_emb]), 1e-20, 1.0)
    ┆   ), 1) * tf.reshape(self.rewards, [-1])
)   

g_opt = self.g_optimizer(self.learning_rate)

self.g_grad, _ = tf.clip_by_global_norm(tf.gradients(self.g_loss, self.g_params), self.grad_clip)

##更新生成器参数
self.g_updates = g_opt.apply_gradients(zip(self.g_grad, self.g_params))

在$tensorflow$ 可以自动的反向求导，所以许多细节不需要在代码中显示。

整体算法流程

利用$MLE$ 方法$pretrain$ 生成器、判别器，这部分上面已经讲过。
下面稍微详细讲下$g\_step、d\_step$。

G_step

1. 利用生成器生成一批假样本。注意生成器每一步都是生成一个在$vocab$ 上的分布，我们以某种方式抽样一个$token$ 作为本步生成的$token$。
2. 在$MLE$ 作为目标函数时，我们需得到$true\_data$ 中当前步的$token$ 在当前生成分布中的概率，在SeqGAN 中考虑的是当前步得到的 $token$ 在生成分布中的概率以及该$token$ 的 $reward$，我们利用蒙特卡洛树搜索法得到每个 $token$ 的 $reward$。
3. 利用$policygradient$ 更新生成器的参数。

实现代码：

for total_batch in range(TOTAL_BATCH):
    # Train the generator for one step
    for it in range(1):
    ┆   samples = generator.generate(sess)##生成器生成一批序列
	    ## 获得序列中每个token 的reward
    ┆   rewards = rollout.get_reward(sess, samples, 16, discriminator)
		## 将序列与其对应的reward 喂给生成器，以policy gradient更新生成器
    ┆   feed = {generator.x: samples, generator.rewards: rewards}
    ┆   _ = sess.run(generator.g_updates, feed_dict=feed)

以上就是训练生成器的过程， 在这个阶段，判别器不发生改变只是对当前的生成情况做出反馈，也就是$reward$ 。

D_step

利用上面已经训完的生成器生成一批样本作为假样本，加上已有的一批真样本，作为训练数据，来训练一个二分类的判别器。

实现代码：

for _ in range(5):
    generate_samples(sess, generator, BATCH_SIZE, generated_num, negative_file)
    dis_data_loader.load_train_data(positive_file, negative_file)

    for _ in range(3):
    ┆   dis_data_loader.reset_pointer()
    ┆   for it in xrange(dis_data_loader.num_batch):
    ┆   ┆   x_batch, y_batch = dis_data_loader.next_batch()
    ┆   ┆   feed = { 
    ┆   ┆   ┆   discriminator.input_x: x_batch,
    ┆   ┆   ┆   discriminator.input_y: y_batch,
    ┆   ┆   ┆   discriminator.dropout_keep_prob: dis_dropout_keep_prob
    ┆   ┆   }   
    ┆   ┆   _ = sess.run(discriminator.train_op, feed)

个人总结与疑点

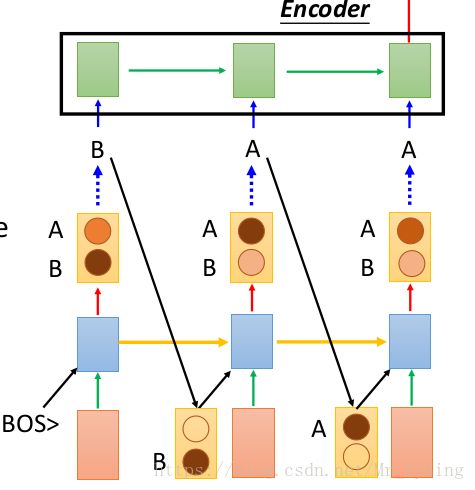
• 如果用传统的$GAN$ 网络来做$NLP$ 的任务，那么生成器生成的序列需要喂给判别器，然后利用判别器来反向的纠正生成器，这个时候梯度的微调不再适用在离散的数据上，并且梯度在回传时可能会有一些困难。如下图：

生成器是以某种方式采样生成一批数据传给判别器的，这样判别器反向将梯度回传给生成器时貌似不太好办？

而在$SeqGan$ 中，生成器每生成一个$token$ 时，都会计算该$token$ 在生成分别中的概率，并且利用上一次训完的判别器计算出相应的$reward$，这个$reward$ 可以理解为生成该$token$ 的权重？经过几轮的训练后，$reward$ 越大的$token$ 越正向，越容易生成（这其实是强化学习的思想）。这里面就不需要判别器反向传梯度给生成器了。这就避免了梯度的微调导致不适用在离散的样本上？

不知道上面我个人的理解是否正确？如有想法欢迎留言讨论。

• 开头就说了传统的$seq2seq$ 方法存在$exposurebias$ 问题，在本篇论文中，生成器只是在$pretrain$ 时用了$true\_data$ 来做$MLE$ ，而在真正训练生成器的时候，生成器并没有用到$true\_data$，只是在判别器 中用到了$true\_data$ 来训练生成器 ，训练好的生成器能得到更好、更准确的$reward$。那么无论在$train$，还是在$decode$ 阶段，其生成器的输入时一致的，不存在在$train$ 时用$train\_data$ 作为$decoder\_input$ ，而在预测的时候用$previous\_out$。