IT经典面试题-逻辑题（附参考答案）

 标？的我不明白，求大神解惑

• 周雯的妈妈是豫林水泥厂的化验员。一天，周雯来到化验室做作业。做完后想出去玩。"等等，妈妈还要考你一个题目，"她接着说，"你看这6只做化验用的玻璃杯，前面3只盛满了水，后面3只是空的。你能只移动1只玻璃杯，就便盛满水的杯子和空杯子间隔起来吗?"爱动脑筋的周雯，是学校里有名的"小机灵"，她只想了一会儿就做到了。请你想想看，"小机灵"是怎样做的?
• 设杯子编号为ABCDEF，ABC为满，DEF为空，把B中的水倒进E中即可。
• ？三个小伙子同时爱上了一个姑娘，为了决定他们谁能娶这个姑娘，他们决定用手枪进行一次决斗。小李的命中率是30％，小黄比他好些，命中率是50％，最出色的枪手是小林，他从不失误，命中率是100％。由于这个显而易见的事实，为公平起见，他们决定按这样的顺序：小李先开枪，小黄第二，小林最后。然后这样循环，直到他们只剩下一个人。那么这三个人中谁活下来的机会最大呢？他们都应该采取什么样的策略？
• 小林在轮到自己且小黄没死的条件下必杀黄，再跟菜鸟李单挑。
  所以黄在林没死的情况下必打林，否则自己必死。
  小李经过计算比较（过程略），会决定自己先打小林。
  于是经计算，小李有873/2600≈33.6%的生机；
  小黄有109/260≈41.9%的生机；
  小林有24.5%的生机。
  哦，这样，那小李的第一枪会朝天开，以后当然是打敌人，谁活着打谁；
  小黄一如既往先打林，小林还是先干掉黄，冤家路窄啊！
  最后李，黄，林存活率约38：27：35； 菜鸟活下来抱得美人归的几率大。
  李先放一空枪（如果合伙干中林，自己最吃亏）黄会选林打一枪（如不打林，自己肯定先玩完了）林会选黄打一枪（毕竟它命中率高）李黄对决0.3:0.280.4可能性李林对决0.3:0.60.6可能性成功率0.73李和黄打林李黄对决0.3:0.40.7*0.4可能性李林对决0.3:0.7*0.6*0.70.7*0.6可能性成功率0.64
• ？在一张长方形的桌面上放了n个一样大小的圆形硬币。这些硬币中可能有一些不完全在桌面内，也可能有一些彼此重叠；当再多放一个硬币而它的圆心在桌面内时，新放的硬币便必定与原先某些硬币重叠。请证明整个桌面可以用4n个硬币完全覆盖。
• 要想让新放的硬币不与原先的硬币重叠，两个硬币的圆心距必须大于直径。也就是说，对于桌面上任意一点，到最近的圆心的距离都小于2，所以，整个桌面可以用n个半径为2的硬币覆盖。 把桌面和硬币的尺度都缩小一倍，那么，长、宽各是原桌面一半的小桌面，就可以用n个半径为1的硬币覆盖。那么，把原来的桌子分割成相等的4块小桌子，那么每块小桌子都可以用n个半径为1的硬币覆盖，因此，整个桌面就可以用4n个半径为1的硬币覆盖。
• 一个球、一把长度大约是球的直径2/3长度的直尺.你怎样测出球的半径？
• 
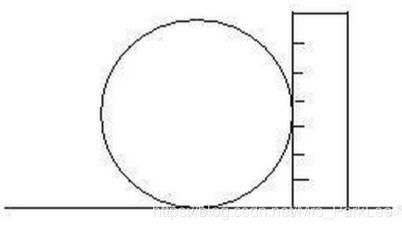
• 五个大小相同的一元人民币硬币。要求两两相接触，应该怎么摆？
• 
• 猜牌问题S先生、P先生、Q先生他们知道桌子的抽屉里有16张扑克牌：红桃A、Q、4黑桃J、8、4、2、7、3草花K、Q、5、4、6方块A、5。约翰教授从这16张牌中挑出一张牌来，并把这张牌的点数告诉P先生，把这张牌的花色告诉Q先生。这时，约翰教授问P先生和Q先生：你们能从已知的点数或花色中推知这张牌是什么牌吗？于是，S先生听到如下的对话：P先生：我不知道这张牌。Q先生：我知道你不知道这张牌。P先生：现在我知道这张牌了。Q先生：我也知道了。听罢以上的对话，S先生想了一想之后，就正确地推出这张牌是什么牌。请问：这张牌是什么牌？
• 方块5
• ？在一张长方形的桌面上放了n个一样大小的圆形硬币。这些硬币中可能有一些不完全在桌面内，也可能有一些彼此重叠；当再多放一个硬币而它的圆心在桌面内时，新放的硬币便必定与原先某些硬币重叠。请证明整个桌面可以用4n个硬币完全覆盖。
• 要想让新放的硬币不与原先的硬币重叠，两个硬币的圆心距必须大于直径。也就是说，对于桌面上任意一点，到最近的圆心的距离都小于2，所以，整个桌面可以用n个半径为2的硬币覆盖。 把桌面和硬币的尺度都缩小一倍，那么，长、宽各是原桌面一半的小桌面，就可以用n个半径为1的硬币覆盖。那么，把原来的桌子分割成相等的4块小桌子，那么每块小桌子都可以用n个半径为1的硬币覆盖，因此，整个桌面就可以用4n个半径为1的硬币覆盖。
• U2合唱团在17分钟 内得赶到演唱会场，途中必需跨过一座桥，四个人从桥的同一端出发，你得帮助他们到达另一端，天色很暗，而他们只有一只手电筒。一次同时最多可以有两人一起过桥，而过桥的时候必须持有手电筒，所以就得有人把手电筒带来带去，来回桥两端。手电筒是不能用丢的方式来传递的。四个人的步行速度各不同，若两人同行则 以较慢者的速度为准。Bono需花1分钟过桥，Edge需花2分钟过桥，Adam需花5分钟过桥，Larry需花10分钟过桥。他们要如何在17分钟内过桥呢？
• 2＋1先过 2
  然后1回来送手电筒 1
  5＋10再过 10
  2回来送手电筒 2
  2＋1过去 2
  总共2＋1＋10＋2＋2＝17分钟
• 芯片测试：有2k块芯片，已知好芯片比坏芯片多．请设计算法从其中找出一片 好芯片，说明你所用的比较次数上限． 其中：好芯片和其它芯片比较时，能正确给出另一块芯片是好还是坏． 坏芯片和其它芯片比较时，会随机的给出好或是坏。
• 把第一块芯片与其它逐一对比，看看其它芯片对第一块芯片给出的是好是坏，如果给出是好的过半，那么说明这是好芯片，完毕。如果给出的是坏的过半，说明第一块芯片是坏的，那么就要在那些在给出第一块芯片是坏的芯片中，重复上述步骤，直到找到好的芯片为止。
• 1，11，21，1211，111221，下一个数是什么？
• 下行是对上一行的解释 所以新的应该是3个1 2个2 1个1 ：312211
• 烧一根不均匀的绳要用一个小时，如何用它来判断半个小时？烧一根不均匀的绳,从头烧到尾总共需要1个小时。现在有若干条材质相同的绳子,问如何用烧绳的方法来计时一个小时十五分钟呢?
• 一，一根绳子从两头烧，烧完就是半个小时。
  二，一根要一头烧，一根从两头烧，两头烧完的时候（30分），将剩下的一根另一端点着，烧尽就是45分钟。再从两头点燃第三根，烧尽就是1时15分。
• ？共有三类药，分别重1g,2g,3g，放到若干个瓶子中，现在能确定每个瓶子中只有其中一种药，且每瓶中的药片足够多，能只称一次就知道各个瓶子中都是盛的哪类药吗？如果有4类药呢？5类呢？N类呢(N可数)？如果是共有m个瓶子盛着n类药呢(m，n)为正整数，药的质量各不相同但各种药的质量已知)？你能只称一次就知道每瓶的药是什么吗？
• 当然是有代价的，称过的药我们就不用了第一个瓶子拿出一片，第二个瓶子拿出四片，第三个拿出十六片...第m个拿出n+1的m-1次方片。把所有这些药片放在一起称重量。
• 有一个大西瓜,用水果刀平整地切,总共切9刀,最多能切成多少份,最少能切成多少份?主要是过程，结果并不是最重要的
• 最少10，最多130
  见下表，表中蓝色部分服从2为底的指数函数规律，红色部分的数值均为其左边与左上
  角的两个数之和。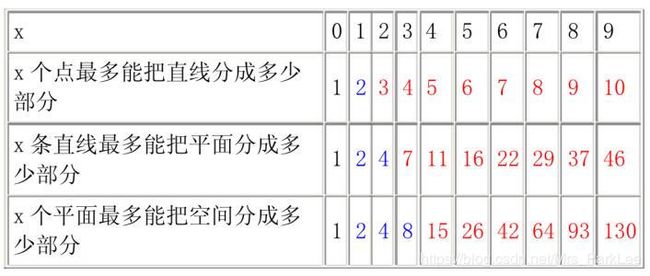
• 
• 一个巨大的圆形水池，周围布满了老鼠洞。猫追老鼠到水池边，老鼠未来得及进洞就掉入水池里。猫继续沿水池边缘企图捉住老鼠（猫不入水）。已知V猫=4V鼠。问老鼠是否有办法摆脱猫的追逐？
• 第一步：游到水池中心。
  第二步：从水池中心游到距中心R/4处，并始终保持鼠、水池中心、猫在一直线上。
  第三步：沿与中心相反方向的直线游3R/4就可以到达水池边，而猫沿圆周到达那里需要3.14R，所以捉不到老鼠。
  三个阶段如下图所示：
• 
• 两个空心球，大小及重量相同，但材料不同。一个是金，一个是铅。空心球表面图有相同颜色的油漆。现在要求在不破坏表面油漆的条件下用简易方法指出哪个是金的，哪个是铅的。
• 旋转看速度，金的密度大，质量相同，所以金球的实际体积较小，因为外半径相同，所以金球的内半径较大，所以金球的转动惯量大，在相同的外加力矩之下，金球的角加速度较小，所以转得慢。
• 有23枚硬币在桌上，10枚正面朝上。假设别人蒙住你的眼睛，而你的手又摸不出硬币的反正面。让你用最好的方法把这些硬币分成两堆，每堆正面朝上的硬币个数相同。
• 分成10＋13两堆， 然后翻转10的那堆。
• 2+7-2+7全部有火柴根组成，移动其中任何一根，答案要求为30说明：因为书写问题作如下解释，2是由横折横三根组成，7是由横折两根组成
  1, 改变赋值号.比如+,-,=
  2, 注意质数.
  3, 可能把画面颠倒过来.
  4, 然后就可以去考虑更改其他数字更改了
• 247-217＝30
• 5个囚犯，分别按1-5号在装有100颗绿豆的麻袋抓绿豆，规定每人至少抓一颗，而抓得最多和最少的人将被处死，而且，他们之间不能交流，但在抓的时候，可以摸出剩下的豆子数。问他们中谁的存活几率最大？
  提示：
  1，他们都是很聪明的人
  2，他们的原则是先求保命，再去多杀人
  3，100颗不必都分完
  4，若有重复的情况，则也算最大或最小，一并处死
• 第一个人选择17时最优的。它有先动优势。他确实有可能被逼死，后面的2、3、4号也想把1号逼死，但做不到（起码确定性逼死做不到）可以看一下，如果第1个人选择21，他的信息时暴露给第2个人的，那么，1号就将自己暴露在一个非常不利的环境下，2-4号就会选择20，五号就会被迫在1-19中选择，则1、5号处死。所以1号不会这样做，会选择一个更小的数。1号选择一个<20的数后，2号没有动力选择一个偏离很大的数（因为这个游戏偏离大会死），只会选择+1或-1，取决于那个死的概率小一些，再考虑这些的时候，又必须逆向考虑，1号必须考虑2-4号的选择，2号必须考虑3、4号的选择，... ...只有5号没得选择，因为前面是只有连着的两个数（且表示为N，N+1），所以5号必死，他也非常明白这一点，会随机选择一个数，来决定整个游戏的命运，但决定不了他自己的命运。
  下面决定的就是1号会选择一个什么数，他仍然不会选择一个太大或太小的数，因为那样仍然是自己处于不利的地位（2-4号肯定不会留情面的），100/6=16.7（为什么除以6？因为5号会随机选择一个数，对1号来说要尽可能的靠近中央，2-4好也是如此，而且正因为2-4号如此，1号才如此... ...），最终必然是在16、17种选择的问题。对16、17进行概率的计算之后，就得出了3个人选择17，第四个人选择16时，为均衡的状态，第4号虽然选择16不及前三个人选择17生存的机会大，但是若选择17则整个游戏的人必死（包括他自己）！第3号没有动力选择16，因为计算概率可知生存机会不如17。
  所以选择为17、17、17、16、X（1-33随机），1-3号生存机会最大。
• 一个商人骑一头驴要穿越1000公里长的沙漠，去卖3000根胡萝卜。已知驴一次性可驮1000根胡萝卜，但每走一公里又要吃掉一根胡萝卜。问：商人共可卖出多少胡萝卜？
• 商人带驴驮1000根胡萝卜，先走250公里，这时，驴已吃250根，放下500根，原地返回，又吃掉250根。商人再带驴驮1000根胡萝卜，走到250公里处，这时，驴已吃250根，再驮上原先放的500根中的250根，继续前行至500公里处，这时，驴又吃250根，放下500根，剩250根返回250公里处，在驮上250公里处剩下的250根返回原地，这时驴又吃250根。商人再带驴驮1000根胡萝卜，走到500公里处，这时，驴已吃500根，再驮上原先放的500根，走出沙漠，驴吃掉500根，还剩500根。
• 10箱黄金，每箱100块，每块一两。有贪官，把某一箱的每块都磨去一钱。请称一次找到不足量的那个箱子。
• 第一箱子拿1块，第二箱子拿2块， 第n箱子拿n块，然后放在一起称，看看缺了几钱，缺了n钱就说明是第n个箱子。
• 有十瓶药，每瓶里都装有100片药（仿佛现在装一百片的少了，都是十片二十片的，不管，咱们就这么来了），其中有八瓶里的药每片重10克，另有两瓶里的药每片重9克。用一个蛮精确的小秤，只称一次，如何找出份量较轻的那两个药瓶？
• 等同于上一题，但此题有一些变化，与众不同的瓶子有两个，只称一次的话，只能得到两个瓶子所缺的克数的总和，我们必须保证能从总和中唯一地得出两个瓶子的所缺数。第一个瓶可拿出1片，第二个拿2片，第三个拿3片，但第四个不能拿4片，因为如果结果缺了5克的话，你就不知道是缺了2+3还是1+4。所以第四个应拿5片，第五个应拿8片，第n个应拿a(n-1)+a(n-2)片。
• 有一辆火车以每小时 15公里的速度离开洛杉矶直奔纽约，另一辆火车以每小时20公里的速度从纽约开往洛杉矶。如果有一只鸟，以30公里每小时的速度和两辆火车同时启动，从洛杉矶出发，碰到另一辆车后返回，依次在两辆火车来回飞行，直到两辆火车相遇，请问，这只小鸟飞行了多长距离？
• 设总距离为d，总共用时d/(15+20)，两车相遇，所以鸟飞了30*d/(15+20)=6d/7
• 你有两个罐子，每个罐子各有若干红色弹球和蓝色弹球，两个罐子共有50个红色弹球，50个蓝色弹球，随机选出一个罐子，随机从中选取出一个弹球，要使取出的是红球的概率最大，一开始两个罐子应放几个红球，几个蓝球？在你的计划中，得到红球的准确几率是多少？
• 一个罐子放1红，一个罐子放49红和50蓝，这样得到红球的概率接近3/4。
• 两个圆环，半径分别是1和2，小圆在大圆内部绕大圆圆周一周，问小圆自身转了几周？如果在大圆的外部，小圆自身转几周呢？
• 把大圆剪断拉直。小圆绕大圆圆周一周，就变成从直线的一头滚至另一头。因为直线长就是大圆的周长，是小圆周长的2倍，所以小圆要滚动2圈。 但是现在小圆不是沿直线而是沿大圆滚动，小圆因此还同时作自转，当小圆沿大圆滚动1周回到原出发点时，小圆同时自转1周。当小圆在大圆内部滚动时自转的方向与滚动的转向相反，所以小圆自身转了1周。当小圆在大圆外部滚动时自转的方向与滚动的转向相同，所以小圆自身转了3周。
  这一题非常有迷惑性，小圆在外部时其实是3圈，你可以拿个硬币试试可以把圆看成一根绳子，长绳是短绳的2倍长，假设长绳开始接口在最底下，短绳接口在长绳接口处，然后短绳开始顺时针绕，当短绳接口对着正左时，这时其实才绕了长绳的1/4，转了180+90度，所以绕一圈是270*4=360*3 。同理小圆在内部时是1圈。也可以套用下列公式： 两圆圆心距/转动者半径=转动者切另一圆时的自转数!!
• 已知： 每个飞机只有一个油箱， 飞机之间可以相互加油（注意是相互，没有加油机） 一箱油可供一架飞机绕地球飞半圈，问题：为使至少一架飞机绕地球一圈回到起飞时的飞机场，至少需要出动几架飞机？（所有飞机从同一机场起飞，而且必须安全返回机场，不允许中途降落，中间没有飞机场）
• 需要3架飞机（记为A，B，C），A走完全程。如下图，黑色箭头表示飞行方向，红色箭头表示一架给另一架加油，红色数字表示加油量整个油箱容量的比值。
• 
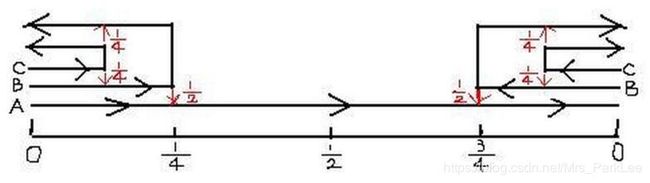
• 在9个点上画10条直线，要求每条直线上有三个点？
• 
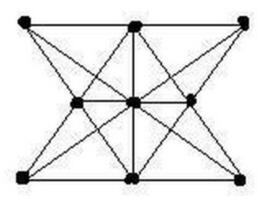
• 在一天的24小时之中，时钟的时针、分针和秒针完全重合在一起的时候有几次？都分别是什么时间？你怎样算出来的？
• 只有两次
  假设时针的角速度是ω（ω=π/6每小时），则分针的角速度为12ω，秒针的角速度为72ω。分针与时针再次重合的时间为t，则有12ωt-ωt=2π，t=12/11小时，换算成时分秒为1小时5分27.3秒，显然秒针不与时针分针重合，同样可以算出其它10次分针与时针重合时秒针都不能与它们重合。只有在正12点和0点时才会重。 证明：将时针视为静止，考察分针，秒针对它的相对速度： 12个小时作为时间单位“1”，“圈/12小时”作为速度单位， 则分针速度为11，秒针速度为719。 由于11与719互质，记12小时/（11*719）为时间单位Δ， 则分针与时针重合当且仅当 t=719kΔ k∈Z 秒针与时针重合当且仅当 t=11jΔ j∈Z 而719与11的最小公倍数为11*719，所以若t=0时三针重合，则下一次三针重合 必然在t=11*719*Δ时，即t=12点。
• 对一批编号为1～100，全部开关朝上(开)的灯进行以下操作：凡是1的倍数反方向拨一次开关；2的倍数反方向又拨一次开关；3的倍数反方向又拨一次开关⋯⋯问：最后为关熄状态的灯的编号。
• 若实际操作求解会相当繁琐。我们知道，就某个亮着的灯而言，如果拨其开关的次数是奇数次，那么，结果它一定是关着的。根据题意可知，号码为N的灯，拨开关的次数等于N的约数的个数，约数个数是奇数，则N一定是平方数。因为10的平方等于100，可知100以内共有10个平方数，即，最后关熄状态的灯共有10盏，编号为1、4、9、16、25、36、49、64、81、100。