- OC语言多界面传值五大方式
Magnetic_h
iosui学习objective-c开发语言
前言在完成暑假仿写项目时,遇到了许多需要用到多界面传值的地方,这篇博客来总结一下比较常用的五种多界面传值的方式。属性传值属性传值一般用前一个界面向后一个界面传值,简单地说就是通过访问后一个视图控制器的属性来为它赋值,通过这个属性来做到从前一个界面向后一个界面传值。首先在后一个界面中定义属性@interfaceBViewController:UIViewController@propertyNSSt
- 2018-07-23-催眠日作业-#不一样的31天#-66小鹿
小鹿_33
预言日:人总是在逃避命运的路上,与之不期而遇。心理学上有个著名的名词,叫做自证预言;经济学上也有一个很著名的定律叫做,墨菲定律;在灵修派上,还有一个很著名的法则,叫做吸引力法则。这3个领域的词,虽然看起来不太一样,但是他们都在告诉人们一个现象:你越担心什么,就越有可能会发生什么。同样的道理,你越想得到什么,就应该要积极地去创造什么。无论是自证预言,墨菲定律还是吸引力法则,对人都有正反2个维度的影响
- 水平垂直居中的几种方法(总结)
LJ小番茄
CSS_玄学语言htmljavascript前端csscss3
1.使用flexbox的justify-content和align-items.parent{display:flex;justify-content:center;/*水平居中*/align-items:center;/*垂直居中*/height:100vh;/*需要指定高度*/}2.使用grid的place-items:center.parent{display:grid;place-item
- 我的烦恼
余建梅
我的烦恼。女儿问我:“你给学生布置什么作文题目?”“《我的烦恼》。”“他们都这么大了,你觉得他们还有烦恼吗?”“有啊!每个人都会有自己烦恼。”“我不相信,大人是没有烦恼的,如果说一定有的话,你的烦恼和我写作业有关,而且是小烦恼。不像我,天天被你说,有这样的妈妈,烦恼是没完没了。”女儿愤愤不平。每个人都会有自己的烦恼,处在上有老下有小的年纪,烦恼多的数不完。想干好工作带好孩子,想孝顺父母又想经营好自
- 【一起学Rust | 设计模式】习惯语法——使用借用类型作为参数、格式化拼接字符串、构造函数
广龙宇
一起学Rust#Rust设计模式rust设计模式开发语言
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档文章目录前言一、使用借用类型作为参数二、格式化拼接字符串三、使用构造函数总结前言Rust不是传统的面向对象编程语言,它的所有特性,使其独一无二。因此,学习特定于Rust的设计模式是必要的。本系列文章为作者学习《Rust设计模式》的学习笔记以及自己的见解。因此,本系列文章的结构也与此书的结构相同(后续可能会调成结构),基本上分为三个部分
- 感赏日志133
马姐读书
图片发自App感赏自己今天买个扫地机,以后可以解放出来多看点书,让这个智能小机器人替我工作了。感赏孩子最近进步很大,每天按时上学,认真听课,认真背书,主动认真完成老师布置的作业。感赏自己明白自己容易受到某人的影响,心情不好,每当此刻我就会舒缓,感赏,让自己尽快抽离,想好的一面。感赏儿子今天在我提醒他事情时,告诉我谢谢妈妈对我的提醒我明白了,而不是说我啰嗦,管事情,孩子更懂事了,懂得感恩了。投射父母
- 关于提高复杂业务逻辑代码可读性的思考
编程经验分享
开发经验java数据库开发语言
目录前言需求场景常规写法拆分方法领域对象总结前言实际工作中大部分时间都是在写业务逻辑,一般都是三层架构,表示层(Controller)接收客户端请求,并对入参做检验,业务逻辑层(Service)负责处理业务逻辑,一般开发都是在这一层中写具体的业务逻辑。数据访问层(Dao)是直接和数据库交互的,用于查数据给业务逻辑层,或者是将业务逻辑层处理后的数据写入数据库。简单的增删改查接口不用多说,基本上写好一
- 拥有断舍离的心态,过精简生活--《断舍离》读书笔记
爱吃丸子的小樱桃
不知不觉间房间里的东西越来越多,虽然摆放整齐,但也时常会觉得空间逼仄,令人心生烦闷。抱着断舍离的态度,我开始阅读《断舍离》这本书,希望从书中能找到一些有效的方法,帮助我实现空间、物品上的断舍离。《断舍离》是日本作家山下英子通过自己的经历、思考和实践总结而成的,整体内涵也从刚开始的私人生活哲学的“断舍离”升华成了“人生实践哲学”,接着又成为每个人都能实行的“改变人生的断舍离”,从“哲学”逐渐升华成“
- DIV+CSS+JavaScript技术制作网页(旅游主题网页设计与制作)云南大理
STU学生网页设计
网页设计期末网页作业html静态网页html5期末大作业网页设计web大作业
️精彩专栏推荐作者主页:【进入主页—获取更多源码】web前端期末大作业:【HTML5网页期末作业(1000套)】程序员有趣的告白方式:【HTML七夕情人节表白网页制作(110套)】文章目录二、网站介绍三、网站效果▶️1.视频演示2.图片演示四、网站代码HTML结构代码CSS样式代码五、更多源码二、网站介绍网站布局方面:计划采用目前主流的、能兼容各大主流浏览器、显示效果稳定的浮动网页布局结构。网站程
- 关于城市旅游的HTML网页设计——(旅游风景云南 5页)HTML+CSS+JavaScript
二挡起步
web前端期末大作业javascripthtmlcss旅游风景
⛵源码获取文末联系✈Web前端开发技术描述网页设计题材,DIV+CSS布局制作,HTML+CSS网页设计期末课程大作业|游景点介绍|旅游风景区|家乡介绍|等网站的设计与制作|HTML期末大学生网页设计作业,Web大学生网页HTML:结构CSS:样式在操作方面上运用了html5和css3,采用了div+css结构、表单、超链接、浮动、绝对定位、相对定位、字体样式、引用视频等基础知识JavaScrip
- HTML网页设计制作大作业(div+css) 云南我的家乡旅游景点 带文字滚动
二挡起步
web前端期末大作业web设计网页规划与设计htmlcssjavascriptdreamweaver前端
Web前端开发技术描述网页设计题材,DIV+CSS布局制作,HTML+CSS网页设计期末课程大作业游景点介绍|旅游风景区|家乡介绍|等网站的设计与制作HTML期末大学生网页设计作业HTML:结构CSS:样式在操作方面上运用了html5和css3,采用了div+css结构、表单、超链接、浮动、绝对定位、相对定位、字体样式、引用视频等基础知识JavaScript:做与用户的交互行为文章目录前端学习路线
- 每日算法&面试题,大厂特训二十八天——第二十天(树)
肥学
⚡算法题⚡面试题每日精进java算法数据结构
目录标题导读算法特训二十八天面试题点击直接资料领取导读肥友们为了更好的去帮助新同学适应算法和面试题,最近我们开始进行专项突击一步一步来。上一期我们完成了动态规划二十一天现在我们进行下一项对各类算法进行二十八天的一个小总结。还在等什么快来一起肥学进行二十八天挑战吧!!特别介绍小白练手专栏,适合刚入手的新人欢迎订阅编程小白进阶python有趣练手项目里面包括了像《机器人尬聊》《恶搞程序》这样的有趣文章
- 没想到,真没想到
一棵落花的树
生活中,每一件小事都蕴藏着他的道理。有些令你意外,却能让你收到更为意外的结果。那一次,我真没想到的事,让我收获了爱。记忆的雨飘落下来,扰乱了我平静的心湖。那是一次数学考试,我破天荒地考了“99”分。我不禁沾沾自喜,这成绩我可不容易得到,妈妈一定会好好表扬我的。回到家,我想妈妈得意的报出成绩,妈妈只是淡淡的说:“嗯,等会儿试卷拿给我看看。”做完作业,我把试卷拿给了妈妈。只见妈妈捧着试卷,眯着眼睛盯着
- 阶段总结反思
轻争
马上就要进入10月份了,今天做一下前段时间的总结和反思。前段时间,日更、英语、健身、护肤坚持的比较好。阅读、书法坚持的不好。1.中间被迫停更半个多月,其余时间一直在坚持日更挑战。偶尔也有不想写的时候,就做一下摘抄。因为阅读(输入)没跟上来,所以写作(输出)质量有待进一步加强。2.英语做到了一周至少学习5天,每次不少于30分钟,但是小班课没有跟上更新速度,下一步要争取利用零碎时间补听小班课。3.减肥
- 【华为OD技术面试真题 - 技术面】- python八股文真题题库(4)
算法大师
华为od面试python
华为OD面试真题精选专栏:华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选**1.Python中的`with`**用途和功能自动资源管理示例:文件操作上下文管理协议示例代码工作流程解析优点2.\_\_new\_\_和**\_\_init\_\_**区别__new____init__区别总结3.**切片(Slicing)操作**基本切片语法
- Python爬虫解析工具之xpath使用详解
eqa11
python爬虫开发语言
文章目录Python爬虫解析工具之xpath使用详解一、引言二、环境准备1、插件安装2、依赖库安装三、xpath语法详解1、路径表达式2、通配符3、谓语4、常用函数四、xpath在Python代码中的使用1、文档树的创建2、使用xpath表达式3、获取元素内容和属性五、总结Python爬虫解析工具之xpath使用详解一、引言在Python爬虫开发中,数据提取是一个至关重要的环节。xpath作为一门
- 主题升华随机抽总结
木棉咕噜
昨天晚上在火山灿教练那里抽了主题升华最后一关。一共抽了两个故事,现总结如下。第一个故事是《并不是你想象的那样》。主题一:有时候,面对别人一些貌似不合常情的行为,不要轻易的指责他,也许背后有我们所不知道的原因。在这一个主题里面,刚开始的时候,我没有加上貌似二字。所以就没有改动之后这么精准。主题二:有时候我们对他人善意的行为,可能会给我们带来一些意外的回报。主题三:面对同样一件事,因为不同的人看待问题
- 学霸父母学渣娃,这孩子真是亲生的?太扎心了!
东北SK皇家成长中心
现在的社会,每个家庭基本都把孩子的教育放在第一位,哪怕父母平时上班再苦再累也不敢在孩子的教育上有丝毫的马虎,平时对孩子的照顾真的是无微不至,每天早起送孩子上学,晚上回家辅导孩子写作业,有的父母的文化程度非常高,但是每每到了辅导孩子写作业这个时候,父母们内心都有这样一种想法,这个孩子真的是我亲生的吗?真想一巴掌拍死他,我上辈子是做了什么孽生出这么一个智障的孩子,家里每每就要上演全武行,看看这些孩子到
- 【无标题】达瓦达瓦
JhonKI
考研
博客主页:https://blog.csdn.net/2301_779549673欢迎点赞收藏⭐留言如有错误敬请指正!本文由JohnKi原创,首发于CSDN未来很长,值得我们全力奔赴更美好的生活✨文章目录前言111️111❤️111111111111111总结111前言111骗骗流量券,嘿嘿111111111111111111111111111️111❤️111111111111111总结11
- 上图为是否色发
JhonKI
考研
博客主页:https://blog.csdn.net/2301_779549673欢迎点赞收藏⭐留言如有错误敬请指正!本文由JohnKi原创,首发于CSDN未来很长,值得我们全力奔赴更美好的生活✨文章目录前言111️111❤️111111111111111总结111前言111骗骗流量券,嘿嘿111111111111111111111111111️111❤️111111111111111总结11
- 143234234123432
JhonKI
考研
博客主页:https://blog.csdn.net/2301_779549673欢迎点赞收藏⭐留言如有错误敬请指正!本文由JohnKi原创,首发于CSDN未来很长,值得我们全力奔赴更美好的生活✨文章目录前言111️111❤️111111111111111总结111前言111骗骗流量券,嘿嘿111111111111111111111111111️111❤️111111111111111总结11
- 女儿考研完报考雅思
捡拾流年
是否我过于焦虑?会不会无形间让女儿觉得压力太大了啊。2022年对于我们家来说是不平常的一年。女儿今年大四,为了准备考研,暑假也没回家,年初去了学校到了年末才回家。女儿自己一个人面对考研,没有参加培训,大四学校作业论文等课业也多,她同时也是很努力复习考研的。在疫情开放很多羊的时期,女儿终于顺顺利利参加12月24、25号的考研,我们和家人都觉得女儿回家来要好好休息调养。可女儿回到家,我再查阅考研信息,
- 1分钟解决 -bash: mvn: command not found,在Centos 7中安装Maven
Energet!c
开发语言
1分钟解决-bash:mvn:commandnotfound,在Centos7中安装Maven检查Java环境1下载Maven2解压Maven3配置环境变量4验证安装5常见问题与注意事项6总结检查Java环境Maven依赖Java环境,请确保系统已经安装了Java并配置了环境变量。可以通过以下命令检查:java-version如果未安装,请先安装Java。1下载Maven从官网下载:前往Apach
- CentOS的根目录下,/bin 和 /sbin 用途和权限
Energet!c
Linux日常centoslinux运维
CentOS的根目录下,/bin和/sbin用途和权限一、/bin(Binary)二、/sbin(SystemBinary)三、总结在CentOS的根目录下,/bin和/sbin目录有不同的用途和权限一、/bin(Binary)用途:存放系统的基本命令,这些命令对所有用户都是可用的。例如:ls、cp、mv、rm等。权限:普通用户和系统管理员都可以使用这些命令。二、/sbin(SystemBinar
- linux 发展史
种树的猴子
内核java操作系统linux大数据
linux发展史说明此前对linux认识模糊一知半解,近期通过学习将自己对于linux的发展总结一下方便大家日后的学习。那Linux是目前一款非常火热的开源操作系统,可是linux是什么时候出现的,又是因为什么样的原因被开发出来的呢。以下将对linux的发展历程进行详细的讲解。目录一、Linux发展背景二、UINIX的诞生三、UNIX的重要分支-BSD的诞生四、Minix的诞生五、GNU与Free
- 又到年末
伊人微语
今天,工作群里,各个部门开始提醒老师们上交各种期末总结资料,才蓦然感觉这个学期已接近尾声,才意识到2022即将过去,新的一年的脚步声已经越来越近不由得生阳一些感慨。年纪大了,感觉到每个日子都是“倏”地一声就过去了,来不及思量,来不及回顾,一年就这么过去了。我常常想,为什么会有这样的感觉呢?年轻时候的每一天是24小时,现在的每一天也不曾少过一分钟,为什么就会感觉到它的脚步越来越快呢?后来我想明白了,
- 戴先华2021.4.18《我的第129篇幸运作业》
39f4298779c4
2021.4.18今天小宝和大表姐出去玩,我和婆婆在烧饭,突然小宝冲了进来,告诉奶奶说:“奶奶,奶奶姐姐在亭子里倒了”我一下子看出小宝的紧张,马上跑了出去,发现大外甥女又患了病,看起来心疼极了,整个人面朝地下的倒下了,在地上不停的抽搐,额头摔了一个大泡,整张脸都是紫色的,眼睛边上都出血了,真的是非常紧张,这么多年姐姐两夫妻就这样看着自己的孩子一次次晕倒,姐夫这么多年,年年都拿不出钱回家,使得家一次
- 大都会资本BMAN的2018年终总结
非线性思考
1投资的本质是认知变现赚钱=足够的认知*高效的的变现。2投资的三大基石策略:提升认知高效变现知行合一3如果你亏钱了要么是认知的问题,要么是变现的问题,要么而是知行合一的问题。4投资需要知行合一,很简单的道理,却拦住了很多高手,是因为认知和行动中间还隔着人性。顶级的高手能把自己从贪嗔痴中抽离出来,顶级高手没有人性,只有原则。5如果你玩的是空气币,就不要幻想拿着它改变世界,那是你套出了幻觉,眼光放短一
- 作业是家庭关系的枢纽
潘海松
回想一下,当孩子做作业的时候,我们不断地在和孩子聊天、沟通,互相提出一些要求,也不可避免地,会产生分歧。举个最常见的例子,我们告诉孩子:「该写作业了。」娃是什么反应?好的亲子关系,孩子会乖乖停掉手里的事马上去写作业,或者好声好气地和家长商量,能不能在半个小时(或某个时间)开始。而不如意的亲子关系,孩子听到这句话的瞬间,就是各种不情愿,敷衍、拖延甚至于撒谎、撒泼打滚。最后,成为当天家庭里坏情绪的引爆
- 2024.9.6 Python,华为笔试题总结,字符串格式化,字符串操作,广度优先搜索解决公司组织绩效互评问题,无向图
RaidenQ
python华为leetcode算法力扣广度优先无向图
1.字符串格式化name="Alice"age=30formatted_string="Name:{},Age:{}".format(name,age)print(formatted_string)或者name="Alice"age=30formatted_string=f"Name:{name},Age:{age}"print(formatted_string)2.网络健康检查第一行有两个整数m
- Java实现的简单双向Map,支持重复Value
superlxw1234
java双向map
关键字:Java双向Map、DualHashBidiMap
有个需求,需要根据即时修改Map结构中的Value值,比如,将Map中所有value=V1的记录改成value=V2,key保持不变。
数据量比较大,遍历Map性能太差,这就需要根据Value先找到Key,然后去修改。
即:既要根据Key找Value,又要根据Value
- PL/SQL触发器基础及例子
百合不是茶
oracle数据库触发器PL/SQL编程
触发器的简介;
触发器的定义就是说某个条件成立的时候,触发器里面所定义的语句就会被自动的执行。因此触发器不需要人为的去调用,也不能调用。触发器和过程函数类似 过程函数必须要调用,
一个表中最多只能有12个触发器类型的,触发器和过程函数相似 触发器不需要调用直接执行,
触发时间:指明触发器何时执行,该值可取:
before:表示在数据库动作之前触发
- [时空与探索]穿越时空的一些问题
comsci
问题
我们还没有进行过任何数学形式上的证明,仅仅是一个猜想.....
这个猜想就是; 任何有质量的物体(哪怕只有一微克)都不可能穿越时空,该物体强行穿越时空的时候,物体的质量会与时空粒子产生反应,物体会变成暗物质,也就是说,任何物体穿越时空会变成暗物质..(暗物质就我的理
- easy ui datagrid上移下移一行
商人shang
js上移下移easyuidatagrid
/**
* 向上移动一行
*
* @param dg
* @param row
*/
function moveupRow(dg, row) {
var datagrid = $(dg);
var index = datagrid.datagrid("getRowIndex", row);
if (isFirstRow(dg, row)) {
- Java反射
oloz
反射
本人菜鸟,今天恰好有时间,写写博客,总结复习一下java反射方面的知识,欢迎大家探讨交流学习指教
首先看看java中的Class
package demo;
public class ClassTest {
/*先了解java中的Class*/
public static void main(String[] args) {
//任何一个类都
- springMVC 使用JSR-303 Validation验证
杨白白
springmvc
JSR-303是一个数据验证的规范,但是spring并没有对其进行实现,Hibernate Validator是实现了这一规范的,通过此这个实现来讲SpringMVC对JSR-303的支持。
JSR-303的校验是基于注解的,首先要把这些注解标记在需要验证的实体类的属性上或是其对应的get方法上。
登录需要验证类
public class Login {
@NotEmpty
- log4j
香水浓
log4j
log4j.rootCategory=DEBUG, STDOUT, DAILYFILE, HTML, DATABASE
#log4j.rootCategory=DEBUG, STDOUT, DAILYFILE, ROLLINGFILE, HTML
#console
log4j.appender.STDOUT=org.apache.log4j.ConsoleAppender
log4
- 使用ajax和history.pushState无刷新改变页面URL
agevs
jquery框架Ajaxhtml5chrome
表现
如果你使用chrome或者firefox等浏览器访问本博客、github.com、plus.google.com等网站时,细心的你会发现页面之间的点击是通过ajax异步请求的,同时页面的URL发生了了改变。并且能够很好的支持浏览器前进和后退。
是什么有这么强大的功能呢?
HTML5里引用了新的API,history.pushState和history.replaceState,就是通过
- centos中文乱码
AILIKES
centosOSssh
一、CentOS系统访问 g.cn ,发现中文乱码。
于是用以前的方式:yum -y install fonts-chinese
CentOS系统安装后,还是不能显示中文字体。我使用 gedit 编辑源码,其中文注释也为乱码。
后来,终于找到以下方法可以解决,需要两个中文支持的包:
fonts-chinese-3.02-12.
- 触发器
baalwolf
触发器
触发器(trigger):监视某种情况,并触发某种操作。
触发器创建语法四要素:1.监视地点(table) 2.监视事件(insert/update/delete) 3.触发时间(after/before) 4.触发事件(insert/update/delete)
语法:
create trigger triggerName
after/before
- JS正则表达式的i m g
bijian1013
JavaScript正则表达式
g:表示全局(global)模式,即模式将被应用于所有字符串,而非在发现第一个匹配项时立即停止。 i:表示不区分大小写(case-insensitive)模式,即在确定匹配项时忽略模式与字符串的大小写。 m:表示
- HTML5模式和Hashbang模式
bijian1013
JavaScriptAngularJSHashbang模式HTML5模式
我们可以用$locationProvider来配置$location服务(可以采用注入的方式,就像AngularJS中其他所有东西一样)。这里provider的两个参数很有意思,介绍如下。
html5Mode
一个布尔值,标识$location服务是否运行在HTML5模式下。
ha
- [Maven学习笔记六]Maven生命周期
bit1129
maven
从mvn test的输出开始说起
当我们在user-core中执行mvn test时,执行的输出如下:
/software/devsoftware/jdk1.7.0_55/bin/java -Dmaven.home=/software/devsoftware/apache-maven-3.2.1 -Dclassworlds.conf=/software/devs
- 【Hadoop七】基于Yarn的Hadoop Map Reduce容错
bit1129
hadoop
运行于Yarn的Map Reduce作业,可能发生失败的点包括
Task Failure
Application Master Failure
Node Manager Failure
Resource Manager Failure
1. Task Failure
任务执行过程中产生的异常和JVM的意外终止会汇报给Application Master。僵死的任务也会被A
- 记一次数据推送的异常解决端口解决
ronin47
记一次数据推送的异常解决
需求:从db获取数据然后推送到B
程序开发完成,上jboss,刚开始报了很多错,逐一解决,可最后显示连接不到数据库。机房的同事说可以ping 通。
自已画了个图,逐一排除,把linux 防火墙 和 setenforce 设置最低。
service iptables stop
- 巧用视错觉-UI更有趣
brotherlamp
UIui视频ui教程ui自学ui资料
我们每个人在生活中都曾感受过视错觉(optical illusion)的魅力。
视错觉现象是双眼跟我们开的一个玩笑,而我们往往还心甘情愿地接受我们看到的假象。其实不止如此,视觉错现象的背后还有一个重要的科学原理——格式塔原理。
格式塔原理解释了人们如何以视觉方式感觉物体,以及图像的结构,视角,大小等要素是如何影响我们的视觉的。
在下面这篇文章中,我们首先会简单介绍一下格式塔原理中的基本概念,
- 线段树-poj1177-N个矩形求边长(离散化+扫描线)
bylijinnan
数据结构算法线段树
package com.ljn.base;
import java.util.Arrays;
import java.util.Comparator;
import java.util.Set;
import java.util.TreeSet;
/**
* POJ 1177 (线段树+离散化+扫描线),题目链接为http://poj.org/problem?id=1177
- HTTP协议详解
chicony
http协议
引言
- Scala设计模式
chenchao051
设计模式scala
Scala设计模式
我的话: 在国外网站上看到一篇文章,里面详细描述了很多设计模式,并且用Java及Scala两种语言描述,清晰的让我们看到各种常规的设计模式,在Scala中是如何在语言特性层面直接支持的。基于文章很nice,我利用今天的空闲时间将其翻译,希望大家能一起学习,讨论。翻译
- 安装mysql
daizj
mysql安装
安装mysql
(1)删除linux上已经安装的mysql相关库信息。rpm -e xxxxxxx --nodeps (强制删除)
执行命令rpm -qa |grep mysql 检查是否删除干净
(2)执行命令 rpm -i MySQL-server-5.5.31-2.el
- HTTP状态码大全
dcj3sjt126com
http状态码
完整的 HTTP 1.1规范说明书来自于RFC 2616,你可以在http://www.talentdigger.cn/home/link.php?url=d3d3LnJmYy1lZGl0b3Iub3JnLw%3D%3D在线查阅。HTTP 1.1的状态码被标记为新特性,因为许多浏览器只支持 HTTP 1.0。你应只把状态码发送给支持 HTTP 1.1的客户端,支持协议版本可以通过调用request
- asihttprequest上传图片
dcj3sjt126com
ASIHTTPRequest
NSURL *url =@"yourURL";
ASIFormDataRequest*currentRequest =[ASIFormDataRequest requestWithURL:url];
[currentRequest setPostFormat:ASIMultipartFormDataPostFormat];[currentRequest se
- C语言中,关键字static的作用
e200702084
C++cC#
在C语言中,关键字static有三个明显的作用:
1)在函数体,局部的static变量。生存期为程序的整个生命周期,(它存活多长时间);作用域却在函数体内(它在什么地方能被访问(空间))。
一个被声明为静态的变量在这一函数被调用过程中维持其值不变。因为它分配在静态存储区,函数调用结束后并不释放单元,但是在其它的作用域的无法访问。当再次调用这个函数时,这个局部的静态变量还存活,而且用在它的访
- win7/8使用curl
geeksun
win7
1. WIN7/8下要使用curl,需要下载curl-7.20.0-win64-ssl-sspi.zip和Win64OpenSSL_Light-1_0_2d.exe。 下载地址:
http://curl.haxx.se/download.html 请选择不带SSL的版本,否则还需要安装SSL的支持包 2. 可以给Windows增加c
- Creating a Shared Repository; Users Sharing The Repository
hongtoushizi
git
转载自:
http://www.gitguys.com/topics/creating-a-shared-repository-users-sharing-the-repository/ Commands discussed in this section:
git init –bare
git clone
git remote
git pull
git p
- Java实现字符串反转的8种或9种方法
Josh_Persistence
异或反转递归反转二分交换反转java字符串反转栈反转
注:对于第7种使用异或的方式来实现字符串的反转,如果不太看得明白的,可以参照另一篇博客:
http://josh-persistence.iteye.com/blog/2205768
/**
*
*/
package com.wsheng.aggregator.algorithm.string;
import java.util.Stack;
/**
- 代码实现任意容量倒水问题
home198979
PHP算法倒水
形象化设计模式实战 HELLO!架构 redis命令源码解析
倒水问题:有两个杯子,一个A升,一个B升,水有无限多,现要求利用这两杯子装C
- Druid datasource
zhb8015
druid
推荐大家使用数据库连接池 DruidDataSource. http://code.alibabatech.com/wiki/display/Druid/DruidDataSource DruidDataSource经过阿里巴巴数百个应用一年多生产环境运行验证,稳定可靠。 它最重要的特点是:监控、扩展和性能。 下载和Maven配置看这里: http
- 两种启动监听器ApplicationListener和ServletContextListener
spjich
javaspring框架
引言:有时候需要在项目初始化的时候进行一系列工作,比如初始化一个线程池,初始化配置文件,初始化缓存等等,这时候就需要用到启动监听器,下面分别介绍一下两种常用的项目启动监听器
ServletContextListener
特点: 依赖于sevlet容器,需要配置web.xml
使用方法:
public class StartListener implements
- JavaScript Rounding Methods of the Math object
何不笑
JavaScriptMath
The next group of methods has to do with rounding decimal values into integers. Three methods — Math.ceil(), Math.floor(), and Math.round() — handle rounding in differen
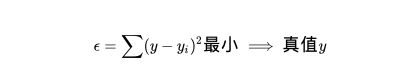
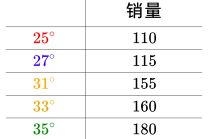
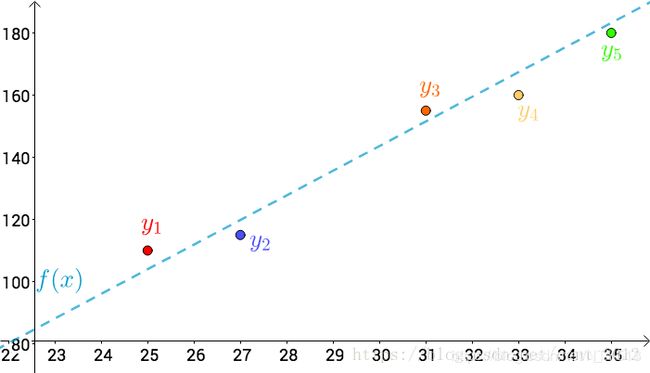
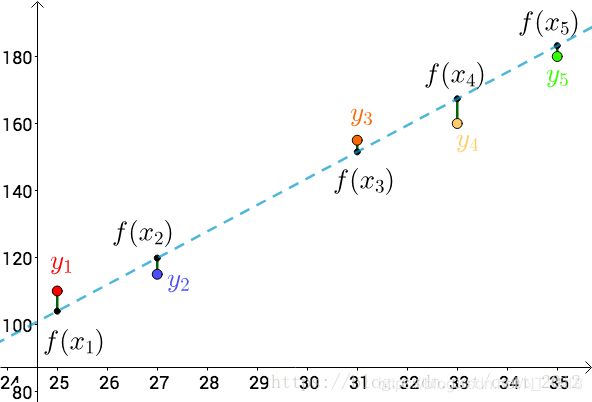

![]()
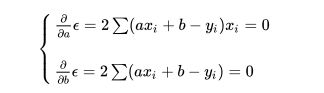
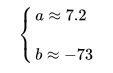

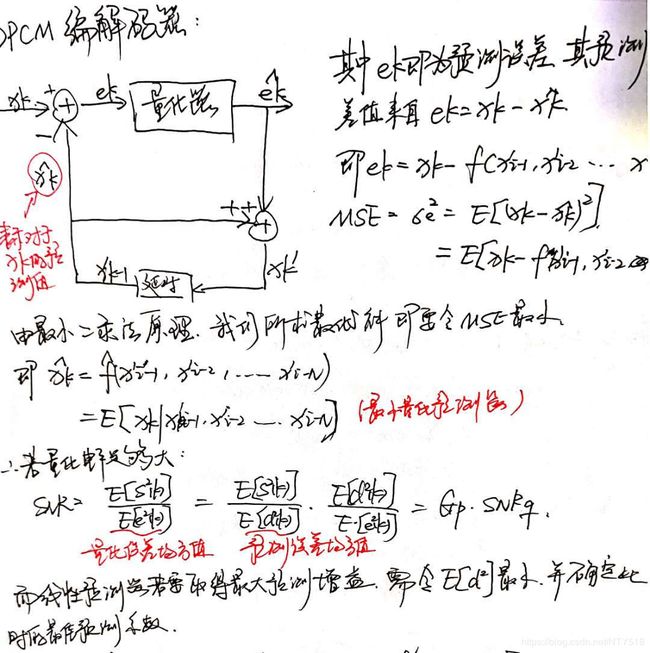


![]()
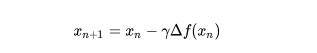

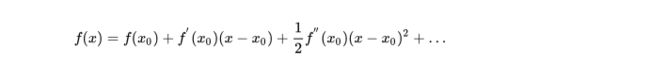
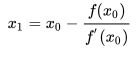
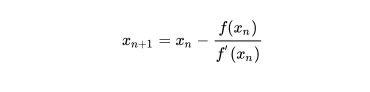
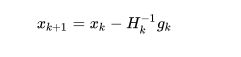

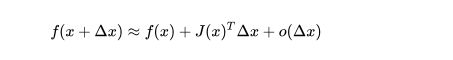
![]()
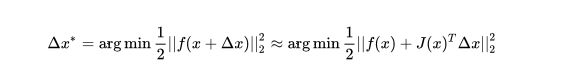

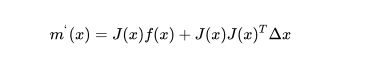
![]()
