决策树学习总结

决策树总结

【写在最前面】
emmmm，课堂笔记的一个总结吧算是。
有任何问题请评论，求轻喷。

决策树是是分类问题中最常用的模型之一，它的优势在于：
  ①能够接受类别型的特征，
  ②分类效果与其他分类算法相当，
  ③训练和测试的效率高。
决策树模型呈树形结构，在分类问题中，表示基于特征对实例进行分类的过程。决策树学习通常包括三个步骤：特征选择、决策树的生成和决策树的修剪。决策树学习常用的算法有ID3、C4.5和CART。

决策树学习

决策函数

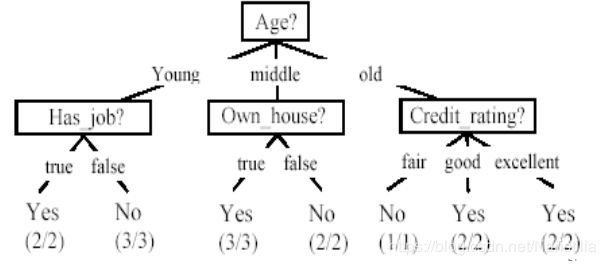
决策树由中间节点和叶子节点构成，中间节点包含决策函数用于决策的特征，叶子节点包含决策结果和类别标签。
对于给定的训练数据，可能存在多棵能够拟合数据的决策树。比如在上图的决策树中，第一层节点用于决策的特征不是Age而是Own_house。如何进行选择？我们需要的是一个与训练数据矛盾较小的决策树，同时具有很好的泛化能力。由于从所有可能的决策树中选取最优决策树是NP完全问题，不能够在多项式时间中找出最优解，因此决策树学习算法通常采用启发式方法来建立次优决策树。

决策树训练算法

使用贪心分治算法来构建决策树，假设所有的特征都是类别型特征，自顶向下递归建树，初始状态为所有训练数据都在根节点上。选择一个最优的特征将训练数据划分成子集，使得各个子集有一个在当前条件下最好的分类。终止条件为：①节点上训练样本都属于同一个类别，②节点上没有训练样本，③没有更多的特征可供选择。

特征选择

这里主要来究竟选择哪个特征更好一些？需要选择合适的特征进行决策，划分数据，生成子节点。“合适”指的是尽量大的减少划分后子数据集的混杂度（尽可能使同一个类别的数据分到同一个子节点中）。我们用熵来度量混杂度。

熵

**熵（entropy）**是表示随机变量不确定性的度量。随机变量$X$是一个取有限个值的离散随机变量，其概率分布为：
$$P(X=x_i)=p_i,i=1,2,...n$$
则随机变量$X$的熵定义为：
$$H(X)=-\sum _{i=1}^n{p}_{i}log{p}_i$$
均匀分布时熵最大，确定分布时熵最小。 （所以需要计算当前条件下使得熵最小的特征）

条件熵

设有随机变量$(X,Y)$，其联合概率分布为：
$$P(X=x_i,Y=y_i)=p_{ij},i=1,2,...,n;j=1,2,...,m$$
** 条件熵（conditional entropy）**$H(Y\mid X)$表示在已知随机变量$X$的条件下随机变量$Y$的不确定性（熵）：
$$H(Y\mid X)=-\sum _{i=1}^n{p}_{i}H(Y\mid X=x_i)$$

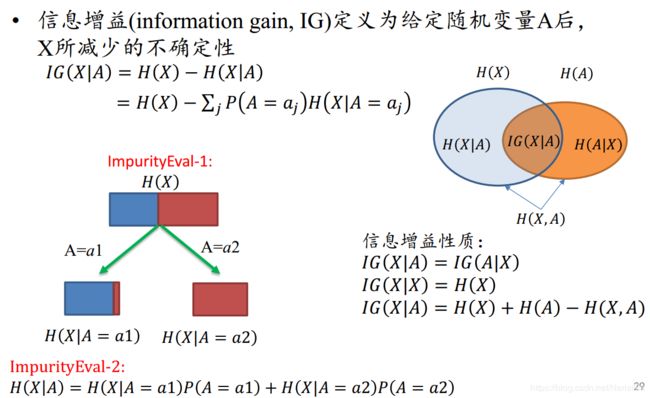
信息增益

信息增益（information gain，IG），特征$A$对训练数据集$D$的信息增益，定义为：
$$IG(D\mid A)=H(D)-H(D\mid A)$$
一般，熵$H(Y)$与条件熵$H(Y\mid X)$之差称为**互信息（mutual information）**也就是说决策树学习中的信息增益相当于训练数据集中类与特征的互信息。
计算每个特征的信息增益，比较大小，选择信息增益最大的特征。

信息增益比

以信息增益作为划分训练数据集的特征，存在【偏向于选择取值较多的特征】的问题，例如：区间划分的越细，区间内纯度越高。
使用 信息增益比（information gain radio） 对这一问题进行校正，这是特征选择的另一准则。信息增益比是信息增益$IG(D\mid A)$与训练数据集$D$关于特征$A$的值的熵$H_A(D)$之比。为什么能得到改善呢？因为$IV(A)$对取值少的属性有所偏好。

决策树的生成

决策树的生成采用贪心策略，从根节点开始扩张（自顶向下），已建立的树不再改变。
每次选择局部信息增益（率）最大的特征划分数据【只考虑当前节点之后选择哪个特征】建立子节点。
对子节点递归调用以上方法，直到达到停止条件（所有特征的信息增益都很小或者没有特征可以选择，early-stopping）停止建树。

ID3算法

划分选择依据：信息增益

C4.5算法

划分选择依据：信息增益率

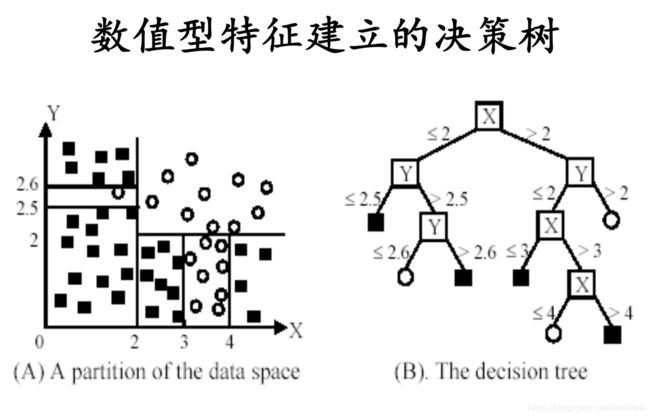
决策树算法对于数值型特征的处理

上面说的都是类别型特征：选择的特征有K个类别，分裂成K个子节点。那么决策树是否能对数值型特征进行处理呢？当然可以TAT。
对于数值型的特征的处理办法通常是将特征离散化，寻找阈值，将数值划分为一个或多个区间。

决策树剪枝

决策树过于复杂很大可能发生过拟合现象，需要对决策树进行简化，这一过程称为剪枝。决策树的剪枝往往通过极小化决策树整体的损失函数来实现，决策树学习的损失函数为，前面是经验风险，后面是结构风险：
$$C_{\alpha }(T)=\sum _{t=1}^{\mid T\mid }{N}_t{H}_t(T)+\alpha \mid T\mid$$
其中$H_t(T)$为经验熵：
$$H_t(T)=-\sum _k\frac{N_{tk}}{N_t}log\frac{N_{tk}}{N_t}$$
剪枝就是当$\alpha$确定时，选择损失函数最小的模型。决策树生成只考虑了通过提高信息增益对训练数据更好的拟合，而决策树剪枝通过优化损失函数还考虑了减小模型复杂度。

两种剪枝方案：
预剪枝（pre-pruning)
提前结束分裂节点。
后剪枝（post-pruning）
常用后剪枝，利用验证集合进行剪枝。

CART分类与回归树

ID3和C4.5都是分类决策树，CART模型由Breiman等人再1984年提出，是广泛的决策树学习方法，既能处理分类问题，又可以用于回归。CART同样由特征选择、树的生成及剪枝组成。
CART假设决策树是二叉树，内部节点特征取值为“是”，“否”。

CART作为分类树

当CART作为分类树时，使用基尼指数来选择最优特征。（大部分时候与熵算出类似的树，但是Gini计算的会快一点【此处存疑】）
基尼指数，分类问题中，假设有$K$个类，样本点属于第$k$类的概率为$p_k$，则概率分布的基尼指数定义为：
$$Gini(p)=\sum _{k=1}^K{p}_k(1-p_k)=1-\sum _{k=1}^K{p}_k^2$$
如果样本集合D根据特征A是否取某一可能值a被分割成$D_1$和$D_2$两部分，即在特征A的条件下，集合D的基尼指数定义为：
$$Gini(D,A)=\frac{\mid D_1\mid }{\mid D\mid }Gini(D_1)+\frac{\mid D_2\mid }{\mid D\mid }Gini(D_2)$$
计算每个特征对该数据集的基尼指数，并根据该特征的每一个取值，将其分成是否两边并计算基尼指数，找到基尼指数最小的那一个，作为最优特征与最优切分点，生成两个子节点。
划分选择依据：最小化基尼指数。具体过程如下图。

CART作为回归树

当CART作为回归树时，使用平方误差最小化准则。

【未完，小概率有后续】

参考资料

统计学习方法，李航
网络数据挖掘课程PPT，徐君
机器学习课程PPT，周晓飞