KD-Tree（C++实现）

参考资料：

https://blog.csdn.net/dymodi/article/details/46830071

https://github.com/WiseDoge/libkdtree

作为存取高维数据的一种数据结构，k-d tree 在静态查询和插入方面的效率还是很高的。本文在这里对 k-d tree 的内容作一些介绍，可能也会结合自己使用 k-d tree 的一些体验作一些点评。其实，k-d tree 是早在1975年的时候由 Stanford 的 Bentley 提出来的。本文的内容也主要来自于他的两篇最原始的文章 [Ben75] 和 [FBF77] 。

k-d tree 概述 与 插入操作（Insertion）
首先，k-d tree 也是二叉搜索树的一种，与常见的平衡二叉搜索树（BST）不同的是，在 k-d tree 中，每个节点内存储的都是一条记录（record），或者说是多维空间中的一个点，用一个向量来表示。而且在 k-d tree中，这个点也代表了空间中的一个区域。每个节点都有两个子节点，而且两个子节点各自代表的区域是父节点的区域一个划分。

在一维的情形中，每条 record 都是由一个单独的 key 来表示的。因此，对于 k-d tree 中的每个节点，key 值小于或者等于当前节点的 key 值的点就属于左子树，比当前节点 key 值大的就属于右子树。因此，这里的 key 值就成为了一种鉴别器（discriminator）。而在 k 维的情况中，一条 record 是由 k 个 key 值来表示的，这里每一维的 key 值都可以作为 discriminator 来将一个点向某个节点的左右子树来分类。而在 k-d tree 中，discriminator 的选取是和该节点所在的层数有关的，即在根节点处，即第0层，按照第一维的 key 值来进行分类，第一维的 key 值小于等于根节点的第一维的 key 值的属于根节点的左子树，大于根节点的第一维的 key 值的属于根节点的右子树。然后在根节点的左右子节点的位置上，即第一层的位置上，根据第二维的 key 值来区分，以此类推。即第 k 层要比较的 key 值的维数为 D=L mod k+1D=L mod k+1 。其中L是当前节点所在的层数，其中根节点即为第0层。

按照 k-d tree 的规则依次插入(0,0), (-10, 10), (10, -10), (-40, -20), (-20, 11), (20, 0)这几个点，我们可以得到如下左图所示的 k-d tree，右图是这几个点在平面的示意图。其中蓝线表示该点处是以第一维的 key 值进行区分，红线表示该点处是以第二维的 key 值进行区分。 

同时我们还可以看出，k-d tree 中每一个节点其实也代表了k维空间中的一个区域（region）。我们以上述几个二维空间中的点为例。根节点 (0,0) 代表的是全平面，即 (-50, -50, 50, 50) 这样一个区域，这里的区域我们用 (xmin,ymin,xmax,ymax)(xmin,ymin,xmax,ymax) 来表示，因为根节点 (0,0) 是在第一维，即 xx 轴出进行区分的，因此它的左子节点就代表了左半平面，右子节点就代表了右半平面。即点 (-10, 10) 代表的是 (-50, -50, 0, 50) 这样一个区域，点 (10, -10) 代表的是 (0, -50, 50, 50) 这样一个区域。以此类推，在点 (-10, 10) 处，因为是第一层，因此按照第二维来区分，所以点 (-40, -20) 的第二维比点 (-10, 10) 小，就在左面；点 (-20, 11) 的第二维比点 (-10, 10) 大，就在右面。而且，左面的点 (-40, -20) 代表的是它的父节点的下半平面，即 (-50, -50, 0, 10) 这样一个区域；右面的点 (-20, 11) 代表的是它的父节点的上半平面，即 (-50, 10, 0, 50) 这样一个区域。

查找操作（Searching）
上面我们介绍了 k-d tree 的原理和插入节点的过程，现在我们介绍下搜索节点的过程。在 k-d tree 中对点进行搜索的方法有很多。包括：（1）对所有维度进行匹配的特定点查询（精确匹配）；（2）对部分维度进行匹配的查询；（3）对某个特定的区域内的点进行进行查询；（4）查找与特定点距离最近的几个点。

上面的几种搜索算法都在 [Ben75] 和 [FBF77] 两篇文章中有详细介绍，在这里我们主要介绍（3），也就是我自己用过的区域查询（Region Query）。区域查询的目标是，在 k-d tree 所代表的空间内，如上面例子中提到的二维平面中的 (-50, -50, 50, 50) 这样一个区域，给定一个矩形的区域（即在各个维度上给出这个区域的上下界），如在上面的例子中我们可以给定 (-45, -30, -30, -10) 这样一个区域，查找所有落在这个区域内的点。

区域查找的主要方法如下：从根节点开始，考察该节点的 key 值所代表的点是否在待查找的区域内，如果在待查区域内，就将这个节点放入一个全局的列表中；在这之后，分别考察该节点的左右子节点所代表区域与待查询的区域是否有交集，如果有，就递归地以该子节点作为根节点，进行上述操作，如果没有就返回。在所有递归函数运行完后，我们可以得到一个全局的列表，这个列表里存储的都是落在待查找区域内的点。从上面的阐述中可以看出，查找算法的复杂度与待查的区域大小有很大关系。虽然根据 [LW77] 的结论，最差情况下区域查找的复杂度会达到 O(kN1−1k)O(kN1−1k)，其中 kk 是数据点的维度， NN 是 k-d tree 内节点的总个数，但 [Ben75, FB74] 的大量仿真都表明在进行超矩形（hyper-rectangular）区域的搜索时，k-d tree 上的区域搜索的表现相当不错（reasonably well）。
 

删除操作（Deletion）
其实，k-d tree 对删除操作的支持并不很好，因为 k-d tree 本身不具备平衡性，动态进行的插入和删除操作可能使得 k-d tree 退化成一个线性表。实际上也有关于平衡 k-d tree 的研究，如 [Rob81]。但可能是因为实现起来太复杂的原因，K-D-B tree 似乎没有得到很多应用。

下面我们主要讲一下删除操作，对 k-d tree 内的节点进行删除的原则是，对于一个没有后继结点的外部节点，删除操作可以直接进行；对于有后继结点的内部节点 PP，要做的就是从它的子节点中找到一个合适的节点 QQ 来放置到这个需要被删除的节点的位置上。而所谓合适的节点，就是说如果 PP 节点是在第 JJ 个维度上进行分界的，那么 QQ 就是 PP 的左子树中 JJ 维上最大的节点，或者是 PP 的右子树中 JJ 维上最小的节点，二者均可以。要将 QQ 节点替换到 PP 节点的位置上去，需要先将 QQ 节点从它原来的位置上删除，因此上面所述的删除操作也是一个递归实现的过程。

我自己写的删除操作因为要结合自己其他的应用，因此写得很冗长，就不在这里放出来了。

优化操作（Optimize）
优化操作是 k-d tree 的一种离线操作。我们都知道，当二叉树随着插入操作的进行，如果无法保证树的平衡性，那么在二叉树上进行操作的复杂度会逐渐变差，极端情况下二叉树会退化成为一个线性表。针对一个不平衡的 k-d tree，可以通过优化的操作来使其恢复平衡，以保证后续查找操作的效率。

所谓优化操作，其实就是按照维度的次序，分别将节点进行排序。比如，对于一个需要优化的 k-d tree，对其所有的节点按照第一维度元素进行升序排序，然后最中间的一个作为根节点，然后左半部分的节点作为主子树的节点，有半部分的节点作为又子树的节点。然后分别对左右子树的节点进行上述的处理，只不过参考的维度分别为第二维，第三维……

经过上面的处理，可以使得一个任意的 k-d tree 成为平衡的 k-d tree。

在这里我们对 k-d tree 的内容进行一个小结，针对已有的 N 个数据点，每个点由一个 k 维的数据表征，建立一个 k-d tree 的复杂度为 O(NlogN)O(Nlog⁡N)，对已有的 k-d tree 进行优化的复杂度为 O(NlogN)O(NlogN)，插入一个节点的复杂度为 O(logN)O(log⁡N)，删除一个节点的复杂度为 O(logN)O(log⁡N)，，进行精确匹配的复杂度为 O(logN)O(log⁡N) ，查找一个特定的区域的最差情况的复杂度为 O(kN1−1k)O(kN1−1k)，但区域查找的复杂度与区域大小有关，而且平均意义下的效果不错。

 

代码如下：

kdtree.h

#ifndef KDTREE_H
#define KDTREE_H

// set dynamic link library
#if defined(_MSC_VER)
#define DLLExport __declspec(dllexport)
#else
#define DLLExport
#endif

// set c++
#ifdef __cplusplus
extern "C" {
#endif

#include 

struct DLLExport tree_node
{
    size_t id;
    size_t split;
    tree_node *left, *right;
};

struct DLLExport tree_model
{
    tree_node *root;
    const float *datas;
    const float *labels;
    size_t n_samples;
    size_t n_features;
    float p;
};

DLLExport void free_tree_memory(tree_node *root);
DLLExport tree_model* build_kdtree(const float *datas, const float *labels,
                                   size_t rows, size_t cols, float p);
DLLExport float* k_nearests_neighbor(const tree_model *model, const float *X_test,
                                     size_t len, size_t k, bool clf);
DLLExport void find_k_nearests(const tree_model *model, const float *coor,
                               size_t k, size_t *args, float *dists);

#ifdef __cplusplus
}
#endif


#endif

kdtree.cpp

#include "kdtree.h"

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

// Example:
//     int x = Malloc(int, 10);
//     int y = (int *)malloc(10 * sizeof(int));
#define Malloc(type, n) (type *)malloc((n)*sizeof(type))

// If you need to use Intel MKL to accelerate,
// you can cancel the next line comment.

//#define USE_INTEL_MKL


#ifdef USE_INTEL_MKL
#include 
#endif

// Clang does not support OpenMP.
#ifndef __clang__

#include 

#endif

// 释放一颗二叉树内存的非递归算法
DLLExport void free_tree_memory(tree_node *root) {
    std::stack node_stack;
    tree_node *p;
    node_stack.push(root);
    while (!node_stack.empty()) {
        p = node_stack.top();
        node_stack.pop();
        if (p->left)
            node_stack.push(p->left);
        if (p->right)
            node_stack.push(p->right);
        free(p);
    }
}


class KDTree {
public:
    KDTree(){}

    KDTree(tree_node *root, const float *datas, size_t rows, size_t cols, float p);

    KDTree(const float *datas, const float *labels,
           size_t rows, size_t cols, float p, bool free_tree = true);

    ~KDTree();

    tree_node *GetRoot() { return root; }

    std::vector> FindKNearests(const float *coor, size_t k);

    std::tuple FindNearest(const float *coor, size_t k) { return FindKNearests(coor, k)[0]; }

    void CFindKNearests(const float *coor, size_t k, size_t *args, float *dists);


private:
    // The sample with the largest distance from point `coor`
    // is always at the top of the heap.
    struct neighbor_heap_cmp {
        bool operator()(const std::tuple &i,
                        const std::tuple &j) {
            return std::get<1>(i) < std::get<1>(j);
        }
    };

    typedef std::tuple neighbor;
    typedef std::priority_queue, neighbor_heap_cmp> neighbor_heap;

    // 搜索 K-近邻时的堆（大顶堆），堆顶始终是 K-近邻中样本点最远的点
    neighbor_heap k_neighbor_heap_;
    // 求距离时的 p, dist(x, y) = pow((x^p + y^p), 1/p)
    float p;
    // 析构时是否释放树的内存
    bool free_tree_;
    // 树根结点
    tree_node *root;
    // 训练集
    const float *datas;
    // 训练集的样本数
    size_t n_samples;
    // 每个样本的维度
    size_t n_features;
    // 训练集的标签
    const float *labels;
    // 寻找中位数时用到的缓存池
    std::tuple *get_mid_buf_;
    // 搜索 K 近邻时的缓存池，如果已经搜索过点 i，令 visited_buf[i] = True
    bool *visited_buf_;

#ifdef USE_INTEL_MKL
    // 使用 Intel MKL 库时的缓存
    float *mkl_buf_;
#endif


    // 初始化缓存
    void InitBuffer();

    // 建树
    tree_node *BuildTree(const std::vector &points);

    // 求一组数的中位数
    std::tuple MidElement(const std::vector &points, size_t dim);

    // 入堆
    void HeapStackPush(std::stack &paths, tree_node *node, const float *coor, size_t k);

    // 获取训练集中第 sample 个样本点第 dim 的值
    float GetDimVal(size_t sample, size_t dim) {
        return datas[sample * n_features + dim];
    }

    // 求点 coor 距离训练集第 i 个点的距离
    float GetDist(size_t i, const float *coor);

    // 寻找切分点
    size_t FindSplitDim(const std::vector &points);

};

// 找到一棵树的 K近邻。Ki 的 id 和  Ki 与 coor 之间的距离 分别保存在   args 和 dists 中
DLLExport
void find_k_nearests(const tree_model *model, const float *coor,
                     size_t k, size_t *args, float *dists) {
    KDTree tree(model->root, model->datas, model->n_samples, model->n_features, model->p);
    std::vector> k_nearest = tree.FindKNearests(coor, k);
    for (size_t i = 0; i < k; ++i) {
        args[i] = std::get<0>(k_nearest[i]);
        dists[i] = std::get<1>(k_nearest[i]);
    }
}

// 建立一棵 KD-Tree
DLLExport
tree_model *build_kdtree(const float *datas, const float *labels,
                         size_t rows, size_t cols, float p) {
    KDTree tree(datas, labels, rows, cols, p, false);
    tree_model *model = Malloc(tree_model, 1);
    model->datas = datas;
    model->labels = labels;
    model->n_features = cols;
    model->n_samples = rows;
    model->root = tree.GetRoot();
    model->p = p;
    return model;
}

// 求平均值，用于回归问题
float mean(const float *arr, size_t len) {
    float ans = 0.0;
    for (size_t i = 0; i < len; ++i)
        ans += arr[i];
    return ans / len;
}

// 投票，用于分类问题
float vote(const float *arr, size_t len) {
    std::unordered_map counter;
    for (size_t i = 0; i < len; ++i) {
        auto t = static_cast(arr[i]);
        if (counter.find(t) == counter.end())
            counter.insert(std::unordered_map::value_type(t, 1));
        else
            counter[t] += 1;
    }
    float cur_arg_max = 0;
    size_t cur_max = 0;
    for (auto &i : counter) {
        if (i.second >= cur_max) {
            cur_arg_max = static_cast(i.first);
            cur_max = i.second;
        }
    }
    return cur_arg_max;
}

DLLExport float *
k_nearests_neighbor(const tree_model *model, const float *X_test, size_t len, size_t k, bool clf) {
    float *ans = Malloc(float, len);
    size_t *args;
    float *dists, *y_pred;
    size_t arr_len;
    int i, j;

#ifdef USE_INTEL_MKL
    int n_procs = omp_get_num_procs();
    assert(n_procs < 100);
    KDTree *trees[100];
    for (size_t i = 0; i < n_procs; ++i)
        trees[i] = new KDTree(model->root, model->datas, model->n_samples, model->n_features, model->p);
    arr_len = k * n_procs;
#else
    arr_len = k;
    KDTree tree(model->root, model->datas, model->n_samples, model->n_features, model->p);
#endif

    args = Malloc(size_t, arr_len);
    dists = Malloc(float, arr_len);
    y_pred = Malloc(float, arr_len);

#ifdef USE_INTEL_MKL
#pragma omp parallel for
    for (i = 0; i < len; ++i)
    {
        int thread_num = omp_get_thread_num();
        trees[thread_num]->CFindKNearests(X_test + i * model->n_features,
            k, args + k * thread_num, dists + k * thread_num);
        for (j = 0; j < k; ++j)
            y_pred[j + k * thread_num] = model->labels[args[j + k * thread_num]];
        if (clf)
            ans[i] = vote(y_pred + k * thread_num, k);
        else
            ans[i] = mean(y_pred + k * thread_num, k);
    }
    for (size_t i = 0; i < n_procs; ++i)
        delete trees[i];

#else
    for (i = 0; i < len; ++i) {
        tree.CFindKNearests(X_test + i * model->n_features, k, args, dists);
        for (j = 0; j < k; ++j)
            y_pred[j] = model->labels[args[j]];
        if (clf)
            ans[i] = vote(y_pred, k);
        else
            ans[i] = mean(y_pred, k);
    }
#endif
    free(args);
    free(y_pred);
    free(dists);
    return ans;
}


inline KDTree::KDTree(tree_node *root, const float *datas, size_t rows, size_t cols, float p) :
        root(root), datas(datas), n_samples(rows),
        n_features(cols), p(p), free_tree_(false) {
    InitBuffer();
    labels = nullptr;
}

inline KDTree::KDTree(const float *datas, const float *labels, size_t rows, size_t cols, float p, bool free_tree) :
        datas(datas), labels(labels), n_samples(rows), n_features(cols), p(p), free_tree_(free_tree) {
    std::vector points;
    for (size_t i = 0; i < n_samples; ++i)
        points.emplace_back(i);
    InitBuffer();
    root = BuildTree(points);
}

inline KDTree::~KDTree() {
    delete[]get_mid_buf_;
    delete[]visited_buf_;
#ifdef USE_INTEL_MKL
    free(mkl_buf_);
#endif
    if (free_tree_)
        free_tree_memory(root);
}

std::vector> KDTree::FindKNearests(const float *coor, size_t k) {
    std::memset(visited_buf_, 0, sizeof(bool) * n_samples);
    std::stack paths;
    tree_node *p = root;

    while (p) {
        HeapStackPush(paths, p, coor, k);
        p = coor[p->split] <= GetDimVal(p->id, p->split) ? p = p->left : p = p->right;
    }
    while (!paths.empty()) {
        p = paths.top();
        paths.pop();

        if (!p->left && !p->right)
            continue;

        if (k_neighbor_heap_.size() < k) {
            if (p->left)
                HeapStackPush(paths, p->left, coor, k);
            if (p->right)
                HeapStackPush(paths, p->right, coor, k);
        } else {
            float node_split_val = GetDimVal(p->id, p->split);
            float coor_split_val = coor[p->split];
            float heap_top_val = std::get<1>(k_neighbor_heap_.top());
            if (coor_split_val > node_split_val) {
                if (p->right)
                    HeapStackPush(paths, p->right, coor, k);

                if ((coor_split_val - node_split_val) < heap_top_val && p->left)
                    HeapStackPush(paths, p->left, coor, k);
            } else {
                if (p->left)
                    HeapStackPush(paths, p->left, coor, k);
                if ((node_split_val - coor_split_val) < heap_top_val && p->right)
                    HeapStackPush(paths, p->right, coor, k);
            }
        }
    }
    std::vector> res;

    while (!k_neighbor_heap_.empty()) {
        res.emplace_back(k_neighbor_heap_.top());
        k_neighbor_heap_.pop();
    }
    return res;
}

void KDTree::CFindKNearests(const float *coor, size_t k, size_t *args, float *dists) {
    std::vector> k_nearest = FindKNearests(coor, k);
    for (size_t i = 0; i < k; ++i) {
        args[i] = std::get<0>(k_nearest[i]);
        dists[i] = std::get<1>(k_nearest[i]);
    }
}


// 初始化缓存

inline void KDTree::InitBuffer() {
    get_mid_buf_ = new std::tuple[n_samples];
    visited_buf_ = new bool[n_samples];

#ifdef USE_INTEL_MKL
    // 要与 C 代码交互，所以用 C 的方式申请内存
    mkl_buf_ = Malloc(float, n_features);
#endif
}

tree_node *KDTree::BuildTree(const std::vector &points) {
    size_t dim = FindSplitDim(points);
    std::tuple t = MidElement(points, dim);
    size_t arg_mid_val = std::get<0>(t);
    float mid_val = std::get<1>(t);

    tree_node *node = Malloc(tree_node, 1);
    node->left = nullptr;
    node->right = nullptr;
    node->id = arg_mid_val;
    node->split = dim;
    std::vector left, right;
    for (auto &i : points) {
        if (i == arg_mid_val)
            continue;
        if (GetDimVal(i, dim) <= mid_val)
            left.emplace_back(i);
        else
            right.emplace_back(i);
    }
    if (!left.empty())
        node->left = BuildTree(left);
    if (!right.empty())
        node->right = BuildTree(right);
    return node;
}

std::tuple KDTree::MidElement(const std::vector &points, size_t dim) {
    size_t len = points.size();
    for (size_t i = 0; i < points.size(); ++i)
        get_mid_buf_[i] = std::make_tuple(points[i], GetDimVal(points[i], dim));
    std::nth_element(get_mid_buf_,
                     get_mid_buf_ + len / 2,
                     get_mid_buf_ + len,
                     [](const std::tuple &i, const std::tuple &j) {
                         return std::get<1>(i) < std::get<1>(j);
                     });
    return get_mid_buf_[len / 2];
}


inline void KDTree::HeapStackPush(std::stack &paths, tree_node *node, const float *coor, size_t k) {
    paths.emplace(node);
    size_t id = node->id;
    if (visited_buf_[id])
        return;
    visited_buf_[id] = true;
    float dist = GetDist(id, coor);
    std::tuple t(id, dist);
    if (k_neighbor_heap_.size() < k)
        k_neighbor_heap_.push(t);

    else if (std::get<1>(t) < std::get<1>(k_neighbor_heap_.top())) {
        k_neighbor_heap_.pop();
        k_neighbor_heap_.push(t);
    }
}

#ifdef USE_INTEL_MKL
inline float KDTree::GetDist(size_t i, const float *coor) {
    size_t idx = i * n_features;
    vsSub(n_features, datas + idx, coor, mkl_buf_);
    vsPowx(n_features, mkl_buf_, p, mkl_buf_);
    float dist = cblas_sasum(n_features, mkl_buf_, 1);
    return static_cast(pow(dist, 1.0 / p));
}
#else

inline float KDTree::GetDist(size_t i, const float *coor) {
    float dist = 0.0;
    size_t idx = i * n_features;
#pragma omp parallel for reduction(+:dist)
    for (int t = 0; t < n_features; ++t)
        dist += pow(datas[idx + t] - coor[t], p);
    return static_cast(pow(dist, 1.0 / p));
}

#endif

size_t KDTree::FindSplitDim(const std::vector &points) {
    if (points.size() == 1)
        return 0;
    size_t cur_best_dim = 0;
    float cur_largest_spread = -1;
    float cur_min_val;
    float cur_max_val;
    for (size_t dim = 0; dim < n_features; ++dim) {
        cur_min_val = GetDimVal(points[0], dim);
        cur_max_val = GetDimVal(points[0], dim);
        for (const auto &id : points) {
            if (GetDimVal(id, dim) > cur_max_val)
                cur_max_val = GetDimVal(id, dim);
            else if (GetDimVal(id, dim) < cur_min_val)
                cur_min_val = GetDimVal(id, dim);
        }

        if (cur_max_val - cur_min_val > cur_largest_spread) {
            cur_largest_spread = cur_max_val - cur_min_val;
            cur_best_dim = dim;
        }
    }
    return cur_best_dim;
}

main.cpp

#include "kdtree.h"
#include 
#include 


int main() {
    float datas[100] = {1.3, 1.3, 1.3,
                         8.3, 8.3, 8.3,
                         2.3, 2.3, 2.3,
                         1.2, 1.2, 1.2,
                         7.3, 7.3, 7.3,
                         9.3, 9.3, 9.3,
                         15, 15, 15,
                         3, 3, 3,
                         1.1, 1.1, 1.1,
                         12, 12, 12,
                         4, 4, 4,
                         5, 5, 5};
    float labels[100];
    for(size_t i = 0; i < 12; ++i)
        labels[i] = (float)i;
    tree_model *model = build_kdtree(datas, labels, 12, 3, 2);
    float test[6] = {3, 3, 3, 4, 4, 4};
    size_t args[100];
    float dists[100];
    find_k_nearests(model, test, 5, args, dists);  // 这里只搜索了（3，3，3）的K邻近点

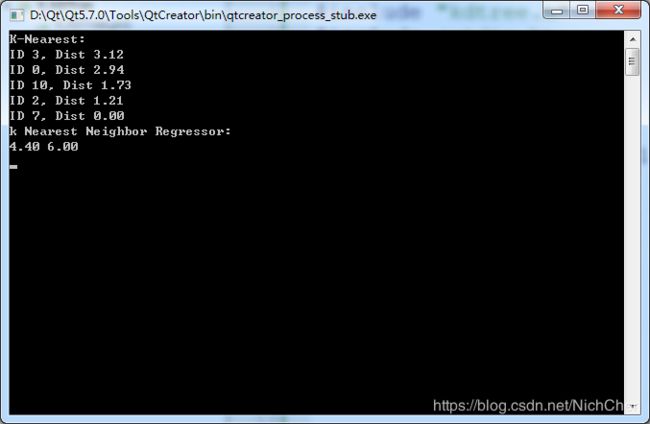
    printf("K-Nearest: \n");
    for (size_t i = 0; i < 5; ++i) {
        printf("ID %d, Dist %.2f\n", args[i], dists[i]);
    }

    float *ans = k_nearests_neighbor(model, test, 2, 5, false);  // 形参2表示：test中有2个样本待测
    printf("k Nearest Neighbor Regressor: \n%.2f %.2f\n", ans[0], ans[1]);

//    tree_node *root = model->root;


    free(ans);
    free_tree_memory(model->root);

    return 0;
}

运行结果