程序的控制结构及random库

title: 程序的控制结构及random库
date: 2020-02-21 14:02:26
tags: python

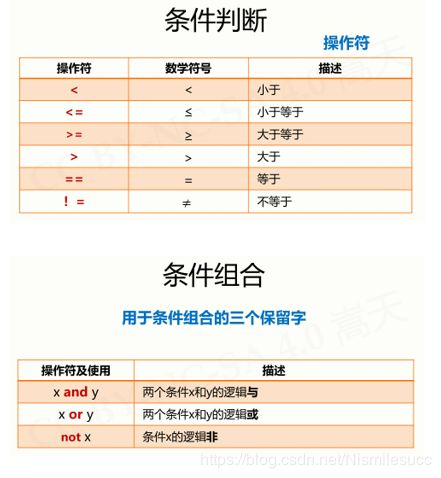
一、程序的控制结构

单分支结构：

if <条件>:
	<语句块>

二分支结构：

if <条件>:
	<语句块1>
else:
	<语句块2>

仅适用于表达简单逻辑的二分支结构的紧凑形式：

<表达式1> if <条件> else <表达式2>

# 举例
g=eval(input())
print("猜{}了".format("对" if g==99 else "错"))

好处：用非常简洁的一行代码来表示二分支结构

需要注意的是：if/else所对应的输出不是语句而是表达式，语句：带赋值形式的有等号构成的语句，紧凑形式不支持带等号的赋值形式

多分支结构：

if <条件1>:
	<语句块1>
elif <条件2>:
	<语句块2>
	...
else:
	<语句块n>

Sample1:身体质量指数BMI

循环的扩展中，else的存在可以让我们知道一段循环是否被break结束

二、random库

是否设定种子，看我们的程序需求，如果需要再现随机过程就设定，如果不关心别人复现的结果，就不设定

import random
random.seed(10)
print(random.random())
print(random.random())
print(random.random())
print(random.random())
print(random.random())

# 种子10对应的序列：
0.5714025946899135
0.4288890546751146
0.5780913011344704
0.20609823213950174
0.81332125135732
...

Sample:圆周率的计算

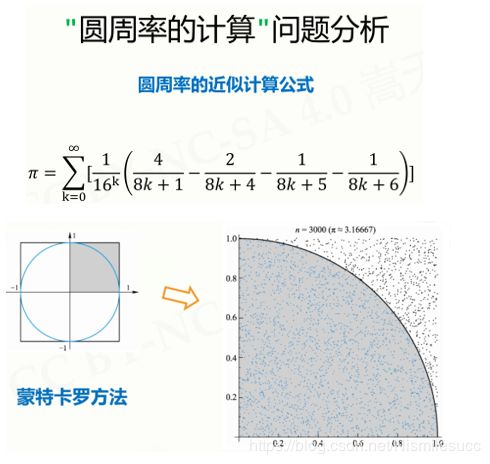
蒙特卡洛法：圆周率是一个圆形，对于一个正方形来说，相当于圆的面积/正方形的面积，这个值和圆周率是有关系的。那么怎么算呢？随机撒很多很多点，在圆内部的点就构成了圆的面积，在正方形中的所有撒点构成了正方形的面积，通过撒点数量的比值，就可以算出圆的面积

近似公式法：

pi=0
n=100
for k in range(n):
    pi+=1/pow(16,k)*(4/(8*k+1)-2/(8*k+4)-1/(8*k+5)-1/(8*k+6))
print("圆周率值是：{}".format(pi))
# 圆周率值是：3.141592653589793

蒙特卡洛法：

from random import random
from time import perf_counter
DARTS=1000*1000 #当前在区域中抛洒点的总数量
hits=0.0 # 目前在圆的内部的点的数量
start=perf_counter()
# 循环撒点的过程
for i in range(1,DARTS+1):
    x,y=random(),random()
    dist=pow(x**2+y**2,0.5)
    # 判断是否在圆内
    if(dist<=1.0):
        hits+=1
pi=4*(hits/DARTS)
print("圆周率的值是：{}".format(pi))
print("运行时间是：{:.5f}s".format(perf_counter()-start))

# 圆周率的值是：3.143448
# 运行时间是：1.35486s

计算思维很重要，比如四色问题，无法用公式求解，但可以通过计算机用计算思维来求解

通过time库可以帮助我们关注程序运行时间及性能，以便对循环等做出优化

本博客学习内容来自mooc 北理Python语言程序设计课程