MATLAB产生特定功率谱密度的高斯白噪声的两种方法
产生方法
假设我们想要的高斯白噪声信号的功率谱密度为k(这里只考虑k为常数的情形)。
1、wgn函数:
noise = wgn(1,N,k*B,'linear'); % 功率P = 功率谱密度*B = k*B;
其中前两个参数表示行列数,第三个参数表示信号功率P,要注意区分功率和功率谱密度的概念。此外,linear表示线性强度(linear power),单位为Watt。如果输入其他:‘dBw’或缺省则表示用dBw作为功率单位,则输入的第三个参数应为10log10(P)=10log10(k*B)‘dBm’表示以dBm作为功率单位,则输入的第三个参数应为10log10(P*1000)=10log10(k*B*1000)。下面会再次对此进行总结。
P(信号功率)=k(信号功率谱密度)* B(带宽); % 这里k为常数;
具体原因是:我们所能产生的噪声总是离散且有限长的,不妨记长度为N,有限长的时域信号对应无限宽的频谱,但是我们只能通过DFT获得有限长的频谱,频谱长度由时域采样间隔td决定,即带宽为B = 1/td,td无法做到无穷小,那么B就不可能无限宽,这表明从频域来看,我们只能获得噪声的长度为 B 的频谱,那么功率谱的频率范围也为B,这样就可以得到P(功率)=k(功率谱密度)* B(带宽)。
我们可以通过下面的代码块来验证:
clear all; close all;
N = 2048; % 噪声点数2048点;
B = 20000; % 带宽20000Hz;
k = 1; % 功率谱密度1;
f = 0-B/2:B/N:B-B/N-B/2; % 频谱列表
noise = wgn(1,N,k*B,'linear'); % 功率P = 功率谱密度*B = k*B;
Nf = fftshift(fft(noise,N)); % 噪声频谱
GN = power(abs(Nf), 2); % 噪声功率谱
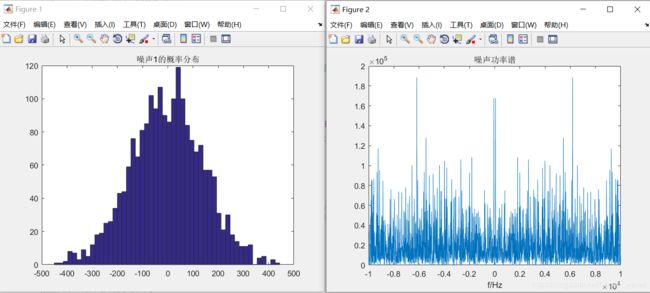
figure; hist(noise, 50);title('噪声1的概率分布');
figure; plot(f,GN/N);title('噪声功率谱');xlabel('f/Hz');
fprintf('噪声功率谱密度均值为:%f\n', mean(GN/N)/B);
2、randn函数
noise = randn(1,N) * ((k*B)^0.5); % 与噪声直接相乘的应该是 功率^0.5(即电压值)
randn直接生成的时域信号,通过乘以一个系数使它的功率谱密度发生改变,这个系数应当是信号的幅值(或者说电压),与噪声直接相乘的应该是 功率^0.5(即电压值)
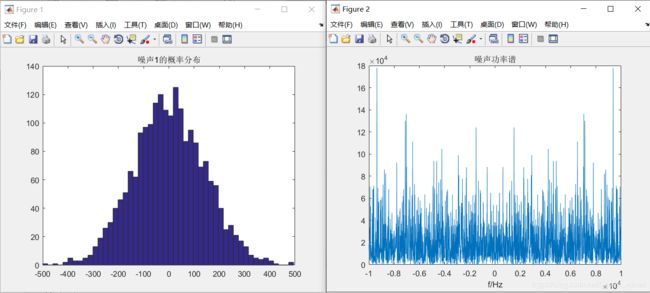

结果也是在1附近,与k值基本吻合。
总结
wgn还可以在输入的末尾添加参数‘real’或‘complex’来获得复噪声信号。对于实信号,我们作以下总结:
% 产生功率谱密度为k的高斯白噪声序列的四种方法:
% (1)noise = randn(1,N) * ((k*B)^0.5); % 噪声——直接相乘的应该是 功率^0.5(即电压值)
% (2)noise = wgn(1,N,k*B,'linear'); % 功率 = 功率谱密度*B = k*B
% (3)noise = wgn(1,N,10*log10(k*B),'dBw'); % 缺省第四个参数结果相同;
% (4)noise = wgn(1,N,10*log10(k*B*1000),'dBm');
其中,输入单位‘dBw’的含义:
将希望得到的 噪声功率 P1 = k*B与 参考功率 P0 = 1W进行比较,计算功率增益,即:
10log10(P1/P0) = 10log10(P1) = 10log10(k*B) dBw
输入单位‘dBm’的含义类似,只是参考功率换成了 P0 = 1mW。
10log10(P1/P0) = 10log10(P1*1000) = 10log10(k*B*1000) dBm