隐马尔科夫模型(HMM)算法的理解与超详细推导
今天看了徐亦达教授的HMM讲解,感觉有所收获,并将隐马尔科夫模型算法的推导整理了一下,帮助大家一起理解这个算法。首先我们通过一个股票的案例来引入这个算法,我们来看看这个股票行情和涨跌观测值的一个状态图:

由图中可以看出,股市的行情分成牛市、熊市和均市,这三种行情是可以互相转化的,并且互相转化是有一定的概率的,这种行情是观测不到的,是一种隐变量,也可以看成是一种状态 q q q,并且在每一个时间点的状态我们可以表示成 q t {q_t} qt,而我们可以观测到的是股市的涨跌,所以我们将涨跌或者是不变看成是观测值 y y y,某一时刻的观测值可以表示成 y t {y_t} yt,所以隐状态和观测值的关系我们可以由下图表示:

根据上图,我们可以将 t − 1 t-1 t−1 时刻到 t t t 时刻状态变换的概率 P ( q t ∣ q t − 1 ) P({q_t}|{q_{t - 1}}) P(qt∣qt−1) 称为转移概率,将 t t t 时刻得到观测值的概率 P ( y t ∣ q t ) P({y_t}|{q_{t}}) P(yt∣qt) 称为发射概率。我们可以将每一种状态下转移的概率写在一起成为转移概率矩阵 A A A,就像上面的股票案例,我们可以得到这个状态图的转移概率矩阵为:
A = [ 0.6 0.2 0.2 0.5 0.3 0.2 0.4 0.1 0.5 ] A= \begin{bmatrix} 0.6 & 0.2 & 0.2 \\ 0.5 & 0.3 & 0.2 \\ 0.4 & 0.1 & 0.5 \end{bmatrix} A=⎣⎡0.60.50.40.20.30.10.20.20.5⎦⎤
看这个矩阵每一行都是一个状态的转移概率,比如第一行表示牛市状态下转移到另外一个状态的概率,0.6表示下一个状态是牛市的概率,剩下的0.2和0.2分别表示牛市转到熊市和均市的概率,矩阵的第一列表示转移到牛市状态的概率,第二列表示转移到熊市的概率,第三列表示转移到均市的概率。每一行表示某个状态,所以说每一行元素相加的值为1。假设有 k k k 种不同的状态, 我们可以将转移概率矩阵用一般的形式表示成:
A k = [ P ( q t = 1 ∣ q t − 1 = 1 ) ⋯ P ( q t = k ∣ q t − 1 = 1 ) ⋮ ⋱ ⋮ P ( q t = 1 ∣ q t − 1 = k ) ⋯ P ( q t = k ∣ q t − 1 = k ) ] {A_k}= \left[ \begin{matrix} P({q_t=1}|{q_{t - 1}=1}) & \cdots & P({q_t=k}|{q_{t - 1}=1}) \\ \vdots & \ddots & \vdots \\ P({q_t=1}|{q_{t - 1}=k}) & \cdots & P({q_t=k}|{q_{t - 1}=k}) \\ \end{matrix} \right] Ak=⎣⎢⎡P(qt=1∣qt−1=1)⋮P(qt=1∣qt−1=k)⋯⋱⋯P(qt=k∣qt−1=1)⋮P(qt=k∣qt−1=k)⎦⎥⎤
嗯,看到这个状态转移概率矩阵是不是很好理解了,矩阵中 q t − 1 {q_{t - 1}} qt−1 表示上一个状态值, q t {q_{t}} qt 表示当前的状态值。有了状态转移概率,我们再来看看观测值,前面我们有提到过,在某种状态下的观测值出现的概率,我们称之为发射概率,有了前面的状态转移概率的基础,我们就很好理解发射概率矩阵了,上面股票行情图的发射概率矩阵 B B B 如下:
B = [ 0.7 0.1 0.2 0.1 0.6 0.3 0.3 0.3 0.4 ] B= \begin{bmatrix} 0.7 & 0.1 & 0.2 \\ 0.1 & 0.6 & 0.3 \\ 0.3 & 0.3 & 0.4 \end{bmatrix} B=⎣⎡0.70.10.30.10.60.30.20.30.4⎦⎤
同样的,在这个矩阵中,第一行表示牛市状态下,股市涨、跌和不变的概率分别是0.7、0.1和0.2,所以说发射概率矩阵每一行元素的和也为1。我们同样可以把发射概率矩阵用一般的形式表达出来:
B k ∗ m = [ P ( y t = 1 ∣ q t = 1 ) ⋯ P ( y t = m ∣ q t = 1 ) ⋮ ⋱ ⋮ P ( y t = 1 ∣ q t = k ) ⋯ P ( y t = m ∣ q t = k ) ] {B_k*m}= \left[ \begin{matrix} P({y_t=1}|{q_{t}=1}) & \cdots & P({y_t=m}|{q_{t}=1}) \\ \vdots & \ddots & \vdots \\ P({y_t=1}|{q_{t}=k}) & \cdots & P({y_t=m}|{q_{t}=k}) \\ \end{matrix} \right] Bk∗m=⎣⎢⎡P(yt=1∣qt=1)⋮P(yt=1∣qt=k)⋯⋱⋯P(yt=m∣qt=1)⋮P(yt=m∣qt=k)⎦⎥⎤
在上述矩阵中, P ( y t = 1 ∣ q t = 1 ) P({y_t=1}|{q_{t}=1}) P(yt=1∣qt=1) 表示在状态 q t = 1 {q_{t}=1} qt=1的时候,观测值为 y t = 1 {y_t=1} yt=1 出现的概率,以此类推,所以在同一种状态下所有观测值出现的概率相加等于1,也就是说在发射概率矩阵中,每一行的元素和为1。有了状态转移概率矩阵和发射概率矩阵的基础之后,我们再来看看下一个问题:在有状态 q 1 {q_1} q1、 q 2 {q_2} q2、 q 3 {q_3} q3 的情况下,出现观测序列 y 1 {y_1} y1、 y 2 {y_2} y2、 y 3 {y_3} y3 的概率。这个问题可以用数学表达式表示成:
P ( y 1 , y 2 , y 3 ) = ∑ q 1 = 1 K ∑ q 2 = 1 K ∑ q 3 = 1 K P ( y 1 , y 2 , y 3 , q 1 , q 2 , q 3 ) P({y_1},{y_2},{y_3}) = \sum\limits_{{q_1} = 1}^K {\sum\limits_{{q_2} = 1}^K {\sum\limits_{{q_3} = 1}^K {P({y_1},{y_2},{y_3},{q_1},{q_2},{q_3})} } } P(y1,y2,y3)=q1=1∑Kq2=1∑Kq3=1∑KP(y1,y2,y3,q1,q2,q3)
在这个数学表达式中,参数 q 1 {q_1} q1、 q 2 {q_2} q2、 q 3 {q_3} q3 可以通过求和消除,抛开求和符号不说,我们看看 P ( y 1 , y 2 , y 3 , q 1 , q 2 , q 3 ) {P({y_1},{y_2},{y_3},{q_1},{q_2},{q_3})} P(y1,y2,y3,q1,q2,q3) 这个表达式,我们看看如何把这个表达式分解,首先我们想到的是贝叶斯公式,我们可以将 P ( y 1 , y 2 , y 3 , q 1 , q 2 , q 3 ) {P({y_1},{y_2},{y_3},{q_1},{q_2},{q_3})} P(y1,y2,y3,q1,q2,q3) 写成如下表达式:
P ( y 1 , y 2 , y 3 , q 1 , q 2 , q 3 ) = P ( y 3 ∣ y 1 , y 2 , q 1 , q 2 , q 3 ) × P ( y 1 , y 2 , q 1 , q 2 , q 3 ) P({y_1},{y_2},{y_3},{q_1},{q_2},{q_3}) = P({y_3}|{y_1},{y_2},{q_1},{q_2},{q_3}) \times P({y_1},{y_2},{q_1},{q_2},{q_3}) P(y1,y2,y3,q1,q2,q3)=P(y3∣y1,y2,q1,q2,q3)×P(y1,y2,q1,q2,q3)
前面我们提到马尔科夫的时候说过,当前的概率只与最近的那个状态有关,用数学表达式就可以表示成:
P ( y 3 ∣ y 1 , y 2 , q 1 , q 2 , q 3 ) = P ( y 3 ∣ q 3 ) P({y_3}|{y_1},{y_2},{q_1},{q_2},{q_3}){\text{ = }}P{\text{(}}{y_3}|{q_3}{\text{)}} P(y3∣y1,y2,q1,q2,q3) = P(y3∣q3)
所以上述的数学表达式可以写成:
P ( y 1 , y 2 , y 3 , q 1 , q 2 , q 3 ) = P ( y 3 ∣ q 3 ) × P ( y 1 , y 2 , q 1 , q 2 , q 3 ) = P ( y 3 ∣ q 3 ) × P ( q 3 ∣ y 1 , y 2 , q 1 , q 2 ) × P ( y 1 , y 2 , q 1 , q 2 ) P({y_1},{y_2},{y_3},{q_1},{q_2},{q_3}) = P({y_3}|{q_3}) \times P({y_1},{y_2},{q_1},{q_2},{q_3}) \\= P({y_3}|{q_3}) \times P({q_3}|{y_1},{y_2},{q_1},{q_2}) \times P({y_1},{y_2},{q_1},{q_2}) P(y1,y2,y3,q1,q2,q3)=P(y3∣q3)×P(y1,y2,q1,q2,q3)=P(y3∣q3)×P(q3∣y1,y2,q1,q2)×P(y1,y2,q1,q2)
好了,到了这一步,我们又可以看到表达式中的第二项 P ( q 3 ∣ y 1 , y 2 , q 1 , q 2 ) P({q_3}|{y_1},{y_2},{q_1},{q_2}) P(q3∣y1,y2,q1,q2),是不是又有想法了?没错,和上面一样,这个表达式同样可以做变换:
P ( q 3 ∣ y 1 , y 2 , q 1 , q 2 ) = P ( q 3 ∣ q 2 ) P({q_3}|{y_1},{y_2},{q_1},{q_2}) = P({q_3}|{q_2}) P(q3∣y1,y2,q1,q2)=P(q3∣q2)
好了,变换之后,原始的数学表达式可以写成:
P ( y 1 , y 2 , y 3 , q 1 , q 2 , q 3 ) = P ( y 3 ∣ q 3 ) × P ( q 3 ∣ q 2 ) × P ( y 1 , y 2 , q 1 , q 2 ) P({y_1},{y_2},{y_3},{q_1},{q_2},{q_3}) = P({y_3}|{q_3}) \times P({q_3}|{q_2}) \times P({y_1},{y_2},{q_1},{q_2}) P(y1,y2,y3,q1,q2,q3)=P(y3∣q3)×P(q3∣q2)×P(y1,y2,q1,q2)
到了这一步,我们可以观察到什么?没错,就是递归,这个数学表达式就体现出了 P ( y 1 , y 2 , y 3 , q 1 , q 2 , q 3 ) P({y_1},{y_2},{y_3},{q_1},{q_2},{q_3}) P(y1,y2,y3,q1,q2,q3) 和 P ( y 1 , y 2 , q 1 , q 2 ) P({y_1},{y_2},{q_1},{q_2}) P(y1,y2,q1,q2) 的递归关系。而 P ( y 3 ∣ q 3 ) P({y_3}|{q_3}) P(y3∣q3) 正表达的是发射概率, P ( q 3 ∣ q 2 ) P({q_3}|{q_2}) P(q3∣q2) 表达的是转移概率。有了这个递归的关系,我们可以一直递归下去,那么原始的数学表达式可以写成:
P ( y 1 , y 2 , y 3 , q 1 , q 2 , q 3 ) = P ( y 3 ∣ q 3 ) × P ( q 3 ∣ q 2 ) × P ( y 2 ∣ q 2 ) × P ( q 2 ∣ q 1 ) × P ( y 1 ∣ q 1 ) × P ( q 1 ) P({y_1},{y_2},{y_3},{q_1},{q_2},{q_3}) = P({y_3}|{q_3}) \times P({q_3}|{q_2}) \times P({y_2}|{q_2}) \times P({q_2}|{q_1}) \times P({y_1}|{q_1}) \times P({q_1}) P(y1,y2,y3,q1,q2,q3)=P(y3∣q3)×P(q3∣q2)×P(y2∣q2)×P(q2∣q1)×P(y1∣q1)×P(q1)
由上述表达式推及一般的表达式,表达式中的参数都可以在转移概率矩阵 A A A 和 发射概率矩阵 B B B 中找到,唯独只有初始的 P ( q 1 ) P({q_1}) P(q1) 的概率无从所知,我们将这个初始状态定义成 π \pi π,那么隐马尔科夫模型的参数可以表示成:
λ = { A , B , π } \lambda = \{ A,B,\pi \} λ={A,B,π}
所以我们可以将初始状态的值表示成 π i = P ( q 1 = i ) {\pi _i} = P({q_1} = i) πi=P(q1=i), 同时状态序列表示成 Q = q 1 , q 2 , . . . , q T Q = {q_1},{q_2},...,{q_T} Q=q1,q2,...,qT, 观测值序列可以表示成 Y = y 1 , y 2 , . . . , y T Y = {y_1},{y_2},...,{y_T} Y=y1,y2,...,yT。那么隐马尔科夫模型有如下三种主要的操作:
1. 估计 P ( Y ∣ λ ) P(Y|\lambda ) P(Y∣λ)
2. λ M L E = arg max λ P ( Y ∣ λ ) {\lambda _{MLE}} = \mathop {\arg \max }\limits_\lambda P(Y|\lambda ) λMLE=λargmaxP(Y∣λ)
3. arg max Q P ( Y ∣ Q , λ ) \mathop {\arg \max }\limits_Q P(Y|Q,\lambda ) QargmaxP(Y∣Q,λ)
我们先看看如何估计 P ( Y ∣ λ ) P(Y|\lambda ) P(Y∣λ),用普通的方法计算就可以得到:
P ( Y ∣ λ ) = ∑ Q [ P ( Y , Q ∣ λ ) ] = ∑ q 1 = 1 k . . . ∑ q T = 1 k [ P ( y 1 , . . . , y T , q 1 , . . . , q T ∣ λ ) ] P(Y|\lambda ) = \sum\limits_Q {[P(Y,Q|\lambda )]} = \sum\limits_{{q_1} = 1}^k {...\sum\limits_{{q_T} = 1}^k {[P({y_1},...,{y_T},{q_1},...,{q_T}|\lambda )]} } P(Y∣λ)=Q∑[P(Y,Q∣λ)]=q1=1∑k...qT=1∑k[P(y1,...,yT,q1,...,qT∣λ)]
按照上面的推导,我们可以将 P ( Y ∣ λ ) P(Y|\lambda ) P(Y∣λ) 写成:
P ( Y ∣ λ ) = ∑ q 1 = 1 k . . . ∑ q T = 1 k P ( q 1 ) P ( y 1 ∣ q 1 ) P ( q 2 ∣ q 1 ) . . . P ( q t ∣ q t − 1 ) P ( y t ∣ q t ) P(Y|\lambda ) = \sum\limits_{{q_1} = 1}^k {...\sum\limits_{{q_T} = 1}^k {P({q_1})P({y_1}|{q_1})P({q_2}|{q_1})...P({q_t}|{q_{t - 1}})P({y_t}|{q_t})} } P(Y∣λ)=q1=1∑k...qT=1∑kP(q1)P(y1∣q1)P(q2∣q1)...P(qt∣qt−1)P(yt∣qt)
用转移概率矩阵元素和发射概率矩阵中的元素表示可以写成:
P ( Y ∣ λ ) = ∑ q 1 = 1 k . . . ∑ q T = 1 k π ( q 1 ) ∏ t = 2 T a q t − 1 , q t ⋅ b q t ( y t ) P(Y|\lambda ) = \sum\limits_{{q_1} = 1}^k {...\sum\limits_{{q_T} = 1}^k {\pi ({q_1})\prod\limits_{t = 2}^T {{a_{{q_{t - 1,}}{q_t}}} \cdot {b_{{q_t}}}({y_t})} } } P(Y∣λ)=q1=1∑k...qT=1∑kπ(q1)t=2∏Taqt−1,qt⋅bqt(yt)
在转移概率矩阵和发射概率矩阵中:
P ( q t = j ∣ q t − 1 = i ) = a i , j P({q_t} = j|{q_{t - 1}} = i) = {a_{i,j}} P(qt=j∣qt−1=i)=ai,j
P ( y t ∣ q t = j ) = b j ( y t ) P({y_t}|{q_t} = j) = {b_j}({y_t}) P(yt∣qt=j)=bj(yt)
按照上述的表达式计算,要计算整个的 P ( Y ∣ λ ) P(Y|\lambda ) P(Y∣λ),整个表达式的计算量达到了 k T {k^T} kT,这无疑是一个巨大的挑战,我们如何简化整个表达式的计算呢?答案是我们可以把整个的时间序列拆分开来,拆分成向前和向后两个部分,每个部分表示一个联合的概率,看成一个整体,就不用考虑局部的概率是怎么样了,整个的时间序列图如下所示,隐藏的信息我用比较浅的颜色标明了:
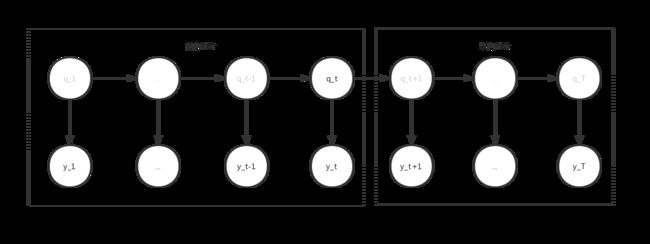
我们为什么要设计一个这样的架构呢,因为用这个通用的模型可以表达任意的状态下的时间序列的条件概率,方便我们的计算。首先我们来看前向部分,我们把前向部分称为 α i ( t ) {\alpha _i}(t) αi(t),表示在 t t t时刻前面所有的时间序列观测值和隐状态的一个联合概率,看做是一个整体,数学表达式为:
α i ( t ) = P ( y 1 , y 2 , . . . , y t , q t = i ∣ λ ) {\alpha _i}(t) = P({y_1},{y_2},...,{y_t},{q_t} = i|\lambda ) αi(t)=P(y1,y2,...,yt,qt=i∣λ)
反向部分表示在 t t t 时刻的状态 i i i 的情况下,也就是前向部分的联合概率情况下,出现 观测序列 y t + 1 , . . . , y T {y_t+1},...,{y_T} yt+1,...,yT 的概率,数学表达式为:
β i ( t ) = P ( y t + 1 , . . . , y T ∣ q t = i , λ ) {\beta _i}(t) = P({y_{t + 1}},...,{y_T}|{q_t} = i,\lambda ) βi(t)=P(yt+1,...,yT∣qt=i,λ)
这么看大家可能有点懵逼,我们先来推导前向的部分吧,首先我们看看前向过程表示在状态 i i i 的时候前面观测值序列的联合概率,总的序列长度为 T T T,那么总的序列 Y Y Y 出现的概率可以表示成:
α i ( t ) = P ( y 1 , y 2 , . . . , y t , q t = i ∣ λ ) ⇒ P ( Y ∣ λ ) = ∑ i = 1 k α i ( T ) {\alpha _i}(t) = P({y_1},{y_2},...,{y_t},{q_t} = i|\lambda ) \Rightarrow P(Y|\lambda ) = \sum\limits_{i = 1}^k {{\alpha _i}(T)} αi(t)=P(y1,y2,...,yt,qt=i∣λ)⇒P(Y∣λ)=i=1∑kαi(T)
为了理解这个 α i ( t ) {\alpha _i}(t) αi(t) 的表达式,我们可以进行一步步递推,首先我们来看 t = 1 t=1 t=1 和 t = 2 t=2 t=2 时候的 α i ( t ) {\alpha _i}(t) αi(t) 吧:
α i ( 1 ) = P ( y 1 , q 1 = i ∣ λ ) = P ( q 1 ) P ( y 1 ∣ q 1 ) = π i b i ( y 1 ) {\alpha _i}(1) = P({y_1},{q_1} = i|\lambda ) = P({q_1})P({y_1}|{q_1}) = {\pi _i}{b_i}({y_1}) αi(1)=P(y1,q1=i∣λ)=P(q1)P(y1∣q1)=πibi(y1)
α j ( 2 ) = P ( y 1 , y 2 , q 2 = j ∣ λ ) = ∑ i = 1 k P ( q 1 = i ) P ( y 1 ∣ q 1 = i ) P ( q 2 = i ∣ q 1 = i ) P ( y 2 ∣ q 2 = j ) = [ ∑ i = 1 k α i ( 1 ) ⋅ a i , j ] ⋅ b j ( y 2 ) {\alpha _j}(2) = P({y_1},{y_2},{q_2} = j|\lambda ) = \sum\limits_{i = 1}^k {P({q_1} = i)P({y_1}|{q_1} = i)} P({q_2} = i|{q_1} = i)P(y2|{q_2} = j) \\ = [\sum\limits_{i = 1}^k {{\alpha _i}(1) \cdot {a_{i,j}}} ] \cdot {b_j}({y_2}) αj(2)=P(y1,y2,q2=j∣λ)=i=1∑kP(q1=i)P(y1∣q1=i)P(q2=i∣q1=i)P(y2∣q2=j)=[i=1∑kαi(1)⋅ai,j]⋅bj(y2)
我们将 α j ( 2 ) {\alpha _j}(2) αj(2) 这个表达式分成三部分来看,第一项 P ( q 1 = i ) P ( y 1 ∣ q 1 = i ) {P({q_1} = i)P({y_1}|{q_1} = i)} P(q1=i)P(y1∣q1=i) 就是 α i ( 1 ) {\alpha _i}(1) αi(1),第二项 P ( q 2 = i ∣ q 1 = i ) P({q_2} = i|{q_1} = i) P(q2=i∣q1=i) 就是我们的转移概率 a i , j {{a_{i,j}}} ai,j,第三项 P ( y 2 ∣ q 2 = j ) P(y2|{q_2} = j) P(y2∣q2=j) 就是在 q 2 q_2 q2 状态下的发射概率,所以 P ( y 2 ∣ q 2 = j ) = b j ( y 2 ) P(y2|{q_2} = j)={b_j}({y_2}) P(y2∣q2=j)=bj(y2),这么拆分来看就比较容易理解了,所以 α i ( 1 ) {\alpha _i}(1) αi(1) 和 α j ( 2 ) {\alpha _j}(2) αj(2) 的递推关系就是:
α j ( 2 ) = [ ∑ i = 1 k α i ( 1 ) ⋅ a i , j ] ⋅ b j ( y 2 ) {\alpha _j}(2) = [\sum\limits_{i = 1}^k {{\alpha _i}(1) \cdot {a_{i,j}}} ] \cdot {b_j}({y_2}) αj(2)=[i=1∑kαi(1)⋅ai,j]⋅bj(y2)
所以我们依据这个递推关系,可以推及到一般形式:
α j ( t + 1 ) = [ ∑ i = 1 k α i ( t ) ⋅ a i , j ] ⋅ b j ( y t + 1 ) {\alpha _j}(t + 1) = [\sum\limits_{i = 1}^k {{\alpha _i}(t) \cdot {a_{i,j}}} ] \cdot {b_j}({y_{t + 1}}) αj(t+1)=[i=1∑kαi(t)⋅ai,j]⋅bj(yt+1)
序列最后的 T T T 时刻的表达式为:
α j ( T ) = [ ∑ i = 1 k α i ( T − 1 ) ⋅ a i , j ] ⋅ b j ( y T ) {\alpha _j}(T) = [\sum\limits_{i = 1}^k {{\alpha _i}(T - 1) \cdot {a_{i,j}}} ] \cdot {b_j}({y_T}) αj(T)=[i=1∑kαi(T−1)⋅ai,j]⋅bj(yT)
这么一来 P ( Y ∣ λ ) = ∑ i = 1 k α i ( T ) P(Y|\lambda ) = \sum\limits_{i = 1}^k {{\alpha _i}(T)} P(Y∣λ)=i=1∑kαi(T) 就是 k ⋅ T k \cdot T k⋅T 项求和,相比之前的指数项,这种算法简化了很多。
同样的道理,我们可以用同样的方法来对反向部分进行推导,只不过反向部分是从后往前进行递归推导的,道理和前向部分的是相同的,具体看下面的表达式推导:
β i ( t ) = P ( y t + 1 , . . . , y T ∣ q t = i , λ ) ⇒ ∑ i = 1 k β i ( 1 ) π i b i ( y 1 ) = P ( Y ∣ λ ) {\beta _i}(t) = P({y_{t + 1}},...,{y_T}|{q_t} = i,\lambda ) \Rightarrow \sum\limits_{i = 1}^k {{\beta _i}(1){\pi _i}{b_i}({y_1})} = P(Y|\lambda ) βi(t)=P(yt+1,...,yT∣qt=i,λ)⇒i=1∑kβi(1)πibi(y1)=P(Y∣λ)
所以我们可以推导在 t t t 时刻 状态 i i i 的时候,出现观测序列 y t + 1 , y t + 2 , . . . , y T {y_{t + 1}},{y_{t + 2}},...,{y_T} yt+1,yt+2,...,yT 的概率:
β i ( T ) = 1 {\beta _i}(T)=1 βi(T)=1 β i ( T − 1 ) = P ( y T ∣ q T − 1 = i ) = ∑ j = 1 k P ( q T = j ∣ q T − 1 = i ) P ( y T ∣ q T = j ) = ∑ j = 1 k a i , j ⋅ b j ( T ) {\beta _i}(T - 1) = P({y_T}|{q_{T - 1}} = i) = \sum\limits_{j = 1}^k {P({q_T} = j|{q_{T - 1}} = i)P({y_T}|{q_T} = j)} = \sum\limits_{j = 1}^k {{a_{i,j}} \cdot {b_j}(T)} βi(T−1)=P(yT∣qT−1=i)=j=1∑kP(qT=j∣qT−1=i)P(yT∣qT=j)=j=1∑kai,j⋅bj(T) β i ( T − 2 ) = P ( y T − 1 , y T ∣ q T − 2 = i ) = ∑ j = 1 k ∑ l = 1 k P ( q T = l ∣ q T − 1 = j ) P ( y T ∣ q T = l ) ⋅ P ( q T − 1 = j ∣ q T − 2 = i ) ⋅ P ( y T − 1 ∣ q T − 1 = j ) = ∑ j = 1 k a i , j ⋅ b j ( y T − 1 ) ⋅ β j ( T − 1 ) {\beta _i}(T - 2) = P({y_{T - 1}},{y_T}|{q_{T - 2}} = i) \\= \sum\limits_{j = 1}^k {\sum\limits_{l = 1}^k {P({q_T} = l|{q_{T - 1}} = j)P({y_T}|{q_T} = l) \cdot P({q_{T - 1}} = j|{q_{T - 2}} = i) \cdot P({y_{T - 1}}|{q_{T - 1}} = j)\\= \sum\limits_{j = 1}^k {{a_{i,j}} \cdot {b_j}({y_{T - 1}}) \cdot {\beta _j}(T - 1)} } } βi(T−2)=P(yT−1,yT∣qT−2=i)=j=1∑kl=1∑kP(qT=l∣qT−1=j)P(yT∣qT=l)⋅P(qT−1=j∣qT−2=i)⋅P(yT−1∣qT−1=j)=j=1∑kai,j⋅bj(yT−1)⋅βj(T−1)
上述表达式中,第一项 ∑ l = 1 k P ( q T = l ∣ q T − 1 = j ) {\sum\limits_{l = 1}^k {P({q_T} = l|{q_{T - 1}} = j)} } l=1∑kP(qT=l∣qT−1=j) 表示 β j ( T − 1 ) {{\beta _j}(T - 1)} βj(T−1),第二项 P ( q T − 1 = j ∣ q T − 2 = i ) {P({q_{T - 1}} = j|{q_{T - 2}} = i)} P(qT−1=j∣qT−2=i) 表示转移概率 a i , j {{a_{i,j}}} ai,j, 第三项 P ( y T − 1 ∣ q T − 1 = j ) {P({y_{T - 1}}|{q_{T - 1}} = j)} P(yT−1∣qT−1=j) 表示发射概率 b j ( y T − 1 ) {{b_j}({y_{T - 1}})} bj(yT−1)。到这里就有了递推的关系,我们可以推及一般的形式:
β i ( t ) = ∑ j = 1 k a i , j ⋅ b j ( y t + 1 ) ⋅ β j ( t + 1 ) {\beta _i}(t) = \sum\limits_{j = 1}^k {{a_{i,j}} \cdot {b_j}({y_{t + 1}}) \cdot {\beta _j}(t + 1)} βi(t)=j=1∑kai,j⋅bj(yt+1)⋅βj(t+1)
一直可以递推到 T = 1 T=1 T=1 的时候:
β i ( 1 ) = ∑ j = 1 k a i , j ⋅ b j ( y 2 ) ⋅ β j ( 2 ) {\beta _i}(1) = \sum\limits_{j = 1}^k {{a_{i,j}} \cdot {b_j}({y_2}) \cdot {\beta _j}(2)} βi(1)=j=1∑kai,j⋅bj(y2)⋅βj(2)
有了上面这些推导,我们可以得到在观测序列 Y Y Y 和时刻 t t t 已知的情况下,在状态 i i i 下的概率:
P ( q t = i ∣ Y , λ ) = P ( Y , q t = i ∣ λ ) P ( Y ∣ λ ) = P ( Y , q t = i ∣ λ ) ∑ j = 1 k P ( Y , q t = i ∣ λ ) = α i ( t ) β i ( t ) ∑ j = 1 k α j ( t ) β j ( t ) P({q_t} = i|Y,\lambda ) = \frac{{P(Y,{q_t} = i|\lambda )}}{{P(Y|\lambda )}} = \frac{{P(Y,{q_t} = i|\lambda )}}{{\sum\limits_{j = 1}^k {P(Y,{q_t} = i|\lambda )} }} = \frac{{{\alpha _i}(t){\beta _i}(t)}}{{\sum\limits_{j = 1}^k {{\alpha _j}(t){\beta _j}(t)} }} P(qt=i∣Y,λ)=P(Y∣λ)P(Y,qt=i∣λ)=j=1∑kP(Y,qt=i∣λ)P(Y,qt=i∣λ)=j=1∑kαj(t)βj(t)αi(t)βi(t)
中间这一步 P ( Y ∣ λ ) = ∑ j = 1 k P ( Y , q t = i ∣ λ ) {P(Y|\lambda )}={\sum\limits_{j = 1}^k {P(Y,{q_t} = i|\lambda )} } P(Y∣λ)=j=1∑kP(Y,qt=i∣λ) 这一步其实就是我们给概率中加上一个中间的隐含变量 q t = i {q_t}=i qt=i,然后通过求和来把它去掉,等式就成立了;还有一个就是分子是如何推导的呢?如下是推导的过程:
P ( Y , q t = i ∣ λ ) = P ( Y ∣ q t = i ) ⋅ P ( q t = i ) = P ( y 1 , . . . , y t ∣ q t = i ) ⋅ P ( y t + 1 , . . . , y T ∣ q t = i ) ⋅ P ( q t = i ) P(Y,{q_t}{\text{ = }}i|\lambda ) = P(Y|{q_t} = i) \cdot P({q_t} = i) = P({y_1},...,{y_t}|{q_t} = i) \cdot P({y_{t + 1}},...,{y_T}|{q_t} = i) \cdot P({q_t} = i) P(Y,qt = i∣λ)=P(Y∣qt=i)⋅P(qt=i)=P(y1,...,yt∣qt=i)⋅P(yt+1,...,yT∣qt=i)⋅P(qt=i)
首先我们把整个表达式的观测值拆分成 y 1 , . . . , y t {y_1},...,{y_t} y1,...,yt 和 y t + 1 , . . . , y T {y_{t + 1}},...,{y_T} yt+1,...,yT 两个部分,然后我们将 P ( q t = i ) P({q_t} = i) P(qt=i) 这一项乘到前面第一项中去可以得到:
P ( Y , q t = i ∣ λ ) = P ( y 1 , . . . , y t , q t = i ) ⋅ P ( y t + 1 , . . . , y T ∣ q t = i ) P(Y,{q_t}{\text{ = }}i|\lambda ) = P({y_1},...,{y_t},{q_t} = i) \cdot P({y_{t + 1}},...,{y_T}|{q_t} = i) P(Y,qt = i∣λ)=P(y1,...,yt,qt=i)⋅P(yt+1,...,yT∣qt=i)
由上述的推导过程,最终我们可以得到:
P ( Y , q t = i ∣ λ ) = α i ( t ) ⋅ β i ( t ) P(Y,{q_t}{\text{ = }}i|\lambda ) = {\alpha _i}(t) \cdot {\beta _i}(t) P(Y,qt = i∣λ)=αi(t)⋅βi(t)
那么最终上述表达式都比较容易理解了。好了,到了这一步,我们先歇一歇,我们看看我之前的一篇博文EM算法理解与推导 ,在这篇博文中,最终得到了EM算法最终的结果:
θ ( g + 1 ) = arg max θ [ Q ( θ , θ ( g ) ) ] = arg max θ ( ∫ Z log ( P ( X , Z ∣ θ ) ) P ( Z ∣ X , θ ( g ) ) d z ) {\theta ^{(g + 1)}} = \mathop {\arg \max }\limits_\theta [Q(\theta ,{\theta ^{(g)}})] = \mathop {\arg \max }\limits_\theta (\int\limits_Z {\log (P(X,Z|\theta ))P(Z|X,{\theta ^{(g)}})dz} ) θ(g+1)=θargmax[Q(θ,θ(g))]=θargmax(Z∫log(P(X,Z∣θ))P(Z∣X,θ(g))dz)
在上述公式中,我们的观测值 Y Y Y 对应上述表达式的 X X X,隐变量 Q Q Q 对应的是 Z Z Z,那么在HMM模型中,我们将EM公式可以改写成:
λ ( g + 1 ) = arg max λ ( ∫ Q log ( P ( Y , Q ∣ λ ) ) ⋅ P ( Q ∣ Y , λ ( g ) ) d Q ) {\lambda ^{(g + 1)}} = \mathop {\arg \max }\limits_\lambda (\int\limits_Q {\log (P(Y,Q|\lambda )) \cdot P(Q|Y,{\lambda ^{(g)}})dQ} ) λ(g+1)=λargmax(Q∫log(P(Y,Q∣λ))⋅P(Q∣Y,λ(g))dQ)
因为此表达式乘以一个 P ( Y ∣ λ ( g ) ) P(Y|{\lambda ^{(g)}}) P(Y∣λ(g)) 是不会影响结果 λ ( g + 1 ) {\lambda ^{(g + 1)}} λ(g+1) 的 ,所以整个表达式可以变换成:
λ ( g + 1 ) = arg max λ ( ∫ Q log ( P ( Y , Q ∣ λ ) ) ⋅ P ( Q , Y ∣ λ ( g ) ) d Q ) {\lambda ^{(g + 1)}} = \mathop {\arg \max }\limits_\lambda (\int\limits_Q {\log (P(Y,Q|\lambda )) \cdot P(Q,Y|{\lambda ^{(g)}})dQ} ) λ(g+1)=λargmax(Q∫log(P(Y,Q∣λ))⋅P(Q,Y∣λ(g))dQ)
到这一步没毛病吧各位老铁,我们继续对这个积分式进行展开,根据之前的推导,我们可以知道:
∫ Q log ( P ( Y , Q ∣ λ ) ) ⋅ P ( Q , Y ∣ λ ( g ) ) d Q = ∑ q 0 = 1 k . . . ∑ q T = 1 k ( log π 0 + ∑ t = 1 T log a q t − 1 , q t + ∑ t = 1 T log b q t ( y t ) ) ⋅ P ( q , Y ∣ λ ( g ) ) \int\limits_Q {\log (P(Y,Q|\lambda )) \cdot P(Q,Y|{\lambda ^{(g)}})dQ} \\= \sum\limits_{{q_0} = 1}^k {...\sum\limits_{{q_T} = 1}^k {(\log {\pi _0} + \sum\limits_{t = 1}^T {\log {a_{{q_{t - 1,}}{q_t}}}} + \sum\limits_{t = 1}^T {\log {b_{{q_t}}}({y_t})} )} } \cdot P(q,Y|{\lambda ^{(g)}}) Q∫log(P(Y,Q∣λ))⋅P(Q,Y∣λ(g))dQ=q0=1∑k...qT=1∑k(logπ0+t=1∑Tlogaqt−1,qt+t=1∑Tlogbqt(yt))⋅P(q,Y∣λ(g))
是不是又懵逼了,其实就是最开始我们推导的递归表达式,最终分成了三项。这三项肯定是无法直接进行计算的,那么我们分别把三项单独计算,就比较方便计算了,我们来看第一项:
Q t e r m 1 = ∑ q 0 = 1 k . . . ∑ q T = 1 k log π q 0 P ( q , Y ∣ λ ( g ) ) = ∑ i = 1 k log π i P ( q 0 = i , Y ∣ λ ( g ) ) {Q^{term1}} = \sum\limits_{{q_0} = 1}^k {...\sum\limits_{{q_T} = 1}^k {\log {\pi _{{q_0}}}P(q,Y|{\lambda ^{(g)}})} = \sum\limits_{i = 1}^k {\log {\pi _i}P({q_0} = i,Y|{\lambda ^{(g)}})} } Qterm1=q0=1∑k...qT=1∑klogπq0P(q,Y∣λ(g))=i=1∑klogπiP(q0=i,Y∣λ(g))
我们的目的是求解 arg max ( Q t e r m 1 ) \arg \max ({Q^{term1}}) argmax(Qterm1) ,首先我们就会想到拉格朗日乘子法,这个算法我们在SVM算法推导的时候经常用到,具体可以参考我之前的一篇博文SVM手动推导,有了最大化的目标函数,我们还差一个限制条件啊,仔细一想,所有状态出现的概率值之和等于1,也就是说 ∑ i = 1 k π i = 1 \sum\limits_{i = 1}^k {{\pi _i}} = 1 i=1∑kπi=1,这样我们就可以得到拉格朗日乘子的表达式,为了区分拉格朗日乘子中的约束项系数与本文中的参数 λ \lambda λ,我们用 τ \tau τ 来代替拉格朗日乘子中的约束项系数,那么对于第一项来说,拉格朗日乘子表达式可以写成:
L M t e r m 1 = ∑ i = 1 k log π i P ( q 0 = i , Y ∣ λ ( g ) ) + τ ( ∑ i = 1 k π i − 1 ) L{M^{term1}} = \sum\limits_{i = 1}^k {\log {\pi _i}P({q_0} = i,Y|{\lambda ^{(g)}}) + \tau (\sum\limits_{i = 1}^k {{\pi _i}} - 1)} LMterm1=i=1∑klogπiP(q0=i,Y∣λ(g))+τ(i=1∑kπi−1)
到了这一步,我们还是使用老的方法,对这个表达式进行求偏导操作:
∂ L M t e r m 1 ∂ π i = P ( q , Y ∣ λ ( g ) ) π i + τ = 0 \frac{{\partial L{M^{term1}}}}{{\partial {\pi _i}}} = \frac{{P(q,Y|{\lambda ^{(g)}})}}{{{\pi _i}}} + \tau = 0 ∂πi∂LMterm1=πiP(q,Y∣λ(g))+τ=0 ∂ L M t e r m 1 ∂ τ = ∑ i = 1 k π i − 1 = 0 \frac{{\partial L{M^{term1}}}}{{\partial \tau }} = \sum\limits_{i = 1}^k {{\pi _i}} - 1 = 0 ∂τ∂LMterm1=i=1∑kπi−1=0
可以推导出:
P ( q 0 = i , Y ∣ λ ( g ) ) = − τ π i P({q_0} = i,Y|{\lambda ^{(g)}}) = - \tau {\pi _i} P(q0=i,Y∣λ(g))=−τπi
将等式两边进行累加,去掉无关的变量:
∑ i = 1 k P ( q 0 = i , Y ∣ λ ( g ) ) = − τ ∑ i = 1 k π i = − τ \sum\limits_{i = 1}^k {P({q_0} = i,Y|{\lambda ^{(g)}})} = - \tau \sum\limits_{i = 1}^k {{\pi _i}} = - \tau i=1∑kP(q0=i,Y∣λ(g))=−τi=1∑kπi=−τ
最终我们可以求出:
π i = P ( q 0 = i , Y ∣ λ ( g ) ) − τ ⇒ π i = P ( q 0 = i , Y ∣ λ ( g ) ) ∑ i = 1 k P ( q 0 = i , Y ∣ λ ( g ) ) {\pi _i} = \frac{{P({q_0} = i,Y|{\lambda ^{(g)}})}}{{ - \tau }} \Rightarrow {\pi _i} = \frac{{P({q_0} = i,Y|{\lambda ^{(g)}})}}{{\sum\limits_{i = 1}^k {P({q_0} = i,Y|{\lambda ^{(g)}})} }} πi=−τP(q0=i,Y∣λ(g))⇒πi=i=1∑kP(q0=i,Y∣λ(g))P(q0=i,Y∣λ(g))
这么一来,我们通过第一项的表达式就可以求出 π i {\pi _i} πi 的值。接下来我们再看第二项表达式,第二项表达式可以写成:
Q t e r m 2 = ∑ q 0 = 1 k . . . ∑ q T = 1 k ∑ t = 1 k log a q t − 1 , q t ⋅ P ( q , Y ∣ λ ( g ) ) = ∑ i = 1 k ∑ j = 1 k ∑ t = 1 k log a i , j ⋅ P ( q t − 1 = i , q t = j , Y ∣ λ ( g ) ) {Q^{term2}} = \sum\limits_{{q_0} = 1}^k {...\sum\limits_{{q_T} = 1}^k {\sum\limits_{t = 1}^k {\log {a_{{q_{t - 1}},{q_t}}} \cdot P(q,Y|{\lambda ^{(g)}})} \\= \sum\limits_{i = 1}^k {\sum\limits_{j = 1}^k {\sum\limits_{t = 1}^k {\log {a_{i,j}} \cdot P({q_{t - 1}} = i,{q_t} = j,Y|{\lambda ^{(g)}})} } } } } Qterm2=q0=1∑k...qT=1∑kt=1∑klogaqt−1,qt⋅P(q,Y∣λ(g))=i=1∑kj=1∑kt=1∑klogai,j⋅P(qt−1=i,qt=j,Y∣λ(g))
因为这一项涉及到状态转移概率,所以我们这一项的约束条件是状态转移概率矩阵中的每一行元素之和为1,所以约束条件可以写成: ∑ i = 1 k τ i ( ∑ j = 1 k a i , j − 1 ) = 0 \sum\limits_{i = 1}^k {{\tau _i}} (\sum\limits_{j = 1}^k {{a_{i,j}}} - 1) = 0 i=1∑kτi(j=1∑kai,j−1)=0,那么完整的拉格朗日表达式可以写成:
L M t e r m 2 = ∑ i = 1 k ∑ j = 1 k ∑ t T log a i , j ⋅ P ( q t − 1 = i , q t = j , Y ∣ λ ( g ) ) + ∑ i = 1 k τ i ( ∑ j = 1 k a i , j − 1 ) L{M^{term2}} = \sum\limits_{i = 1}^k {\sum\limits_{j = 1}^k {\sum\limits_t^T {\log {a_{i,j}} \cdot P({q_{t - 1}} = i,{q_t} = j,Y|{\lambda ^{(g)}})} } } + \sum\limits_{i = 1}^k {{\tau _i}} (\sum\limits_{j = 1}^k {{a_{i,j}}} - 1) LMterm2=i=1∑kj=1∑kt∑Tlogai,j⋅P(qt−1=i,qt=j,Y∣λ(g))+i=1∑kτi(j=1∑kai,j−1)
我们对此拉格朗日表达式求偏导可以得到:
∂ L M t e r m 2 ∂ a i , j = ∑ t = 1 T P ( q t − 1 = i , q t = j , Y ∣ λ ( g ) ) a i , j + ∑ i = 1 k τ i = 0 \frac{{\partial L{M^{term2}}}}{{\partial {a_{i,j}}}} = \frac{{\sum\limits_{t = 1}^T {P({q_{t - 1}} = i,{q_t} = j,Y|{\lambda ^{(g)}})} }}{{{a_{i,j}}}} + \sum\limits_{i = 1}^k {{\tau _i}} = 0 ∂ai,j∂LMterm2=ai,jt=1∑TP(qt−1=i,qt=j,Y∣λ(g))+i=1∑kτi=0 ∂ L M t e r m 2 ∂ τ i = ∑ i = 1 k a i , j − 1 = 0 \frac{{\partial L{M^{term2}}}}{{\partial {\tau _i}}} = \sum\limits_{i = 1}^k {{a_{i,j}}} - 1 = 0 ∂τi∂LMterm2=i=1∑kai,j−1=0
由前面这个表达式可以得到:
∑ t = 1 T P ( q t − 1 = i , q t = j , Y ∣ λ ( g ) ) = − a i , j ∑ i = 1 k τ i ⇒ a i , j = ∑ t = 1 T P ( q t − 1 = i , q t = j , Y ∣ λ ( g ) ) − ∑ i = 1 k τ i \sum\limits_{t = 1}^T {P({q_{t - 1}} = i,{q_t} = j,Y|{\lambda ^{(g)}})} = - {a_{i,j}}\sum\limits_{i = 1}^k {{\tau _i}} \Rightarrow {a_{i,j}} = \frac{{\sum\limits_{t = 1}^T {P({q_{t - 1}} = i,{q_t} = j,Y|{\lambda ^{(g)}})} }}{{ - \sum\limits_{i = 1}^k {{\tau _i}} }} t=1∑TP(qt−1=i,qt=j,Y∣λ(g))=−ai,ji=1∑kτi⇒ai,j=−i=1∑kτit=1∑TP(qt−1=i,qt=j,Y∣λ(g))
将上述表达式两边同时求和,就可以求出 ∑ i = 1 k τ i \sum\limits_{i = 1}^k {{\tau _i}} i=1∑kτi ,计算过程如下所示:
∑ j = 1 k ∑ t = 1 T P ( q t − 1 = i , q t = j , Y ∣ λ ( g ) ) = ∑ j = 1 k − a i , j ∑ i = 1 k π i = − ∑ j = 1 k a i , j ∑ i = 1 k π i \sum\limits_{j = 1}^k {\sum\limits_{t = 1}^T {P({q_{t - 1}} = i,{q_t} = j,Y|{\lambda ^{(g)}})} = \sum\limits_{j = 1}^k { - {a_{i,j}}} \sum\limits_{i = 1}^k {{\pi _i}} = } - \sum\limits_{j = 1}^k {{a_{i,j}}} \sum\limits_{i = 1}^k {{\pi _i}} j=1∑kt=1∑TP(qt−1=i,qt=j,Y∣λ(g))=j=1∑k−ai,ji=1∑kπi=−j=1∑kai,ji=1∑kπi
因为在转移概率矩阵中,每一行元素之和等于1,所以:
− ∑ j = 1 k a i , j ∑ i = 1 k π i = − ∑ i = 1 k π i - \sum\limits_{j = 1}^k {{a_{i,j}}} \sum\limits_{i = 1}^k {{\pi _i}} = - \sum\limits_{i = 1}^k {{\pi _i}} −j=1∑kai,ji=1∑kπi=−i=1∑kπi
将这个值带入到之前的表达式中:
a i , j = ∑ t = 1 T P ( q t − 1 = i , q t = j , Y ∣ λ ( g ) ) ∑ j = 1 k ∑ t = 1 T P ( q t − 1 = i , q t = j , Y ∣ λ ( g ) ) {a_{i,j}} = \frac{{\sum\limits_{t = 1}^T {P({q_{t - 1}} = i,{q_t} = j,Y|{\lambda ^{(g)}})} }}{{\sum\limits_{j = 1}^k {\sum\limits_{t = 1}^T {P({q_{t - 1}} = i,{q_t} = j,Y|{\lambda ^{(g)}})} } }} ai,j=j=1∑kt=1∑TP(qt−1=i,qt=j,Y∣λ(g))t=1∑TP(qt−1=i,qt=j,Y∣λ(g))
在这个表达式中,我们看到分母中 q t = j {q_t}=j qt=j 可以通过求和将其去掉,那么最终的结果是:
a i , j = ∑ t = 1 T P ( q t − 1 = i , q t = j , Y ∣ λ ( g ) ) ∑ t = 1 T P ( q t − 1 = i , Y ∣ λ ( g ) ) {a_{i,j}} = \frac{{\sum\limits_{t = 1}^T {P({q_{t - 1}} = i,{q_t} = j,Y|{\lambda ^{(g)}})} }}{{\sum\limits_{t = 1}^T {P({q_{t - 1}} = i,Y|{\lambda ^{(g)}})} }} ai,j=t=1∑TP(qt−1=i,Y∣λ(g))t=1∑TP(qt−1=i,qt=j,Y∣λ(g))
剩最后一项了,有了前面的推导计算,最后一项的计算也是同样的算法,首先是第三项的表达式:
Q t e r m 3 = ∑ q 0 = 1 k . . . ∑ q T = 1 k ∑ t = 1 T log b q t ( y t ) P ( q , Y ∣ λ ( g ) ) = ∑ j = 1 k ∑ t = 1 T log b j ( y t ) P ( q t = j , Y ∣ λ ( g ) ) {Q^{term3}} = \sum\limits_{{q_0} = 1}^k {...\sum\limits_{{q_T} = 1}^k {\sum\limits_{t = 1}^T {\log {b_{{q_t}}}({y_t})P(q,Y|{\lambda ^{(g)}})} } } = \sum\limits_{j = 1}^k {\sum\limits_{t = 1}^T {\log {b_j}({y_t})P({q_t} = j,Y|{\lambda ^{(g)}})} } Qterm3=q0=1∑k...qT=1∑kt=1∑Tlogbqt(yt)P(q,Y∣λ(g))=j=1∑kt=1∑Tlogbj(yt)P(qt=j,Y∣λ(g))
因为每一种状态的发射概率之和等于1,所以第三项的拉格朗日乘子表达式可以写成:
L M t e r m 3 = ∑ j = 1 k ∑ t = 1 T log b j ( y t ) P ( q t = j , Y ∣ λ ( g ) ) + τ ( ∑ j = 1 k b j ( y t ) − 1 ) L{M^{term3}} = \sum\limits_{j = 1}^k {\sum\limits_{t = 1}^T {\log {b_j}({y_t})P({q_t} = j,Y|{\lambda ^{(g)}}) + \tau (\sum\limits_{j = 1}^k {{b_j}({y_t}) - 1} )} } LMterm3=j=1∑kt=1∑Tlogbj(yt)P(qt=j,Y∣λ(g))+τ(j=1∑kbj(yt)−1)
同样的,我们再来对此拉格朗日表达式求偏导:
∂ L M t e r m 3 ∂ b j ( y t ) = ∑ t = 1 T P ( q t = j , Y ∣ λ ( g ) ) b j ( y t ) + k τ = 0 \frac{{\partial L{M^{term3}}}}{{\partial {b_j}({y_t})}} = \frac{{\sum\limits_{t = 1}^T {P({q_t} = j,Y|{\lambda ^{(g)}})} }}{{{b_j}({y_t})}} + k\tau = 0 ∂bj(yt)∂LMterm3=bj(yt)t=1∑TP(qt=j,Y∣λ(g))+kτ=0 ∂ L M t e r m 3 ∂ τ = ∑ i = 1 k b j ( y t ) − 1 = 0 \frac{{\partial L{M^{term3}}}}{{\partial \tau }} = \sum\limits_{i = 1}^k {{b_j}({y_t})} - 1 = 0 ∂τ∂LMterm3=i=1∑kbj(yt)−1=0
由前面这个表达式可以得到:
∑ t = 1 T P ( q t = j , Y ∣ λ ( g ) ) = − b j ( y t ) τ ⇒ b j ( y t ) = ∑ t = 1 T P ( q t = j , Y ∣ λ ( g ) ) − τ \sum\limits_{t = 1}^T {P({q_t} = j,Y|{\lambda ^{(g)}})} = - {b_j}({y_t})\tau \Rightarrow {b_j}({y_t}) = \frac{{\sum\limits_{t = 1}^T {P({q_t} = j,Y|{\lambda ^{(g)}})} }}{{ - \tau }} t=1∑TP(qt=j,Y∣λ(g))=−bj(yt)τ⇒bj(yt)=−τt=1∑TP(qt=j,Y∣λ(g))
我们再把这个表达式两边求和:
∑ l = 1 k ∑ t = 1 T P ( q t = j , Y = v l ∣ λ ( g ) ) = − τ ∑ l = 1 k b j ( y t = v l ) = − τ \sum\limits_{l = 1}^k {\sum\limits_{t = 1}^T {P({q_t} = j,Y = {v_l}|{\lambda ^{(g)}})} = - \tau \sum\limits_{l = 1}^k {{b_j}({y_t} = {v_l})} } = - \tau l=1∑kt=1∑TP(qt=j,Y=vl∣λ(g))=−τl=1∑kbj(yt=vl)=−τ
最后我们将 τ \tau τ 的结果带入到上述表达式中可以得到最终的发射概率结果:
b j ( y t = v l ) = ∑ t = 1 T P ( q t = j , Y = v l ∣ λ ( g ) ) ∑ j = 1 k ∑ t = 1 T P ( q t = j , Y = v l ∣ λ ( g ) ) {b_j}({y_t} = {v_l}) = \frac{{\sum\limits_{t = 1}^T {P({q_t} = j,Y = {v_l}|{\lambda ^{(g)}})} }}{{\sum\limits_{j = 1}^k {\sum\limits_{t = 1}^T {P({q_t} = j,Y = {v_l}|{\lambda ^{(g)}})} } }} bj(yt=vl)=j=1∑kt=1∑TP(qt=j,Y=vl∣λ(g))t=1∑TP(qt=j,Y=vl∣λ(g))
讲到这里,我们的隐马尔科夫模型算法就推导完了,虽然过程比较复杂,但是慢慢推导还是比较容易理解的,希望这篇HMM算法的推导能帮助大家理解隐马尔科夫模型。文中如有纰漏,也请读者不吝指教;如有转载,请注明出处,谢谢大家。