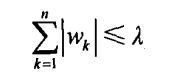Python高级--线性回归、岭回归（岭际线）、lasso回归

知识点小结
1、线性回归模型

from sklearn.linear_model import LinearRegression

lr = LinearRegression()

lr.fit(x。reshape(-1,1),y)

y_ = lr.predict(x.reshape(-1,1))

2、机器学习自带的数据

import sklearn.datasets as datasets
diabetes = datasets.load_diabetes()  #存在本地的数据
datasets.fetch_  #从网路上下载数据

各种线性回归使用方法：

一般情况下 用普通线性回归即可 图片中的情况用rr
如果有很多特征 但是其中的一部分特征肯能是没用的 这个时候可以用lasso试一试

一、原理

1）原理图解

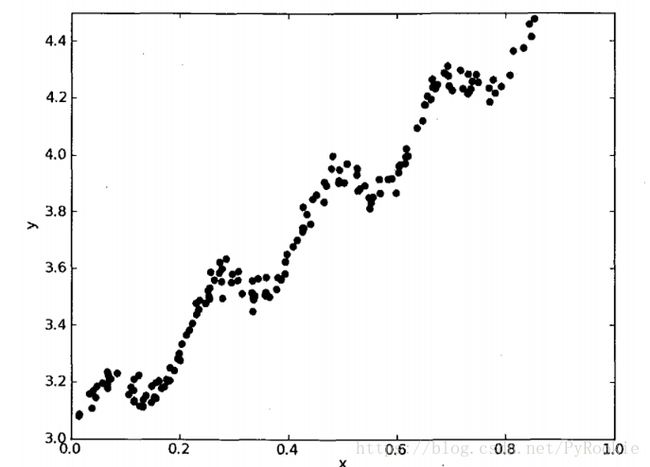
通俗解释线性回归：画一条线，将图上的点都尽量多的压住

原理： 最小二乘法（算法）
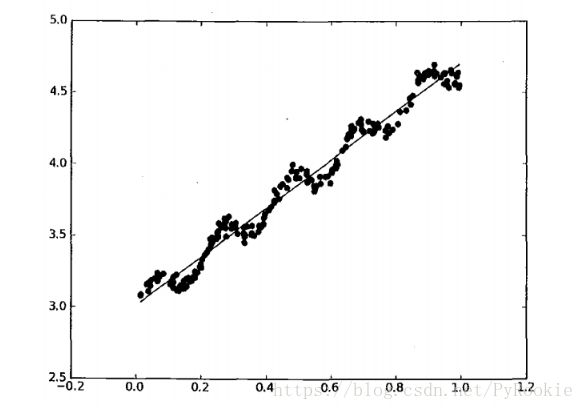
回归曲线: 通过最小二乘法画出回归曲线。

f(x) = wx + b 这个就是一条线的公式

在画图中, 将w称为斜率,b称为偏移(截距)
这里 w(weight)权重 称为b(bias)称为偏差

根据已有的点,通过调整w和b的值,所有点到回归曲线的距离之和最小(点到线的距离也成为损失,目的让损失最小,称为损失函数)

2）功能

给出一些训练数据，使用训练数据训练线性回归模型，再使用训练模型预测结果。 一般用来预测！

二、原理简单演示

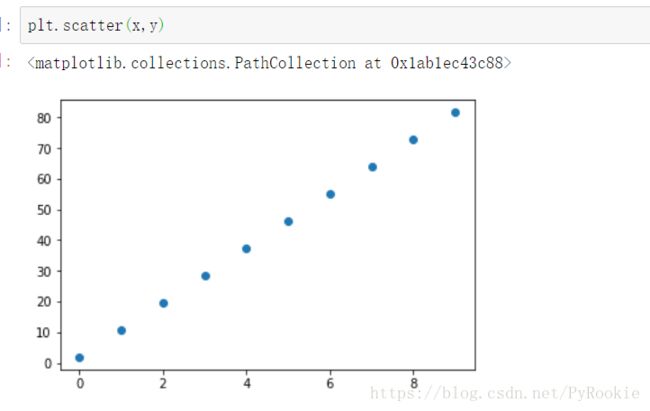
在坐标系上 画出一些点
让机器学习模型通过线性回归 去划线来拟合这些点

1）创建数据

产生一些点

x = np.arange(0,10,1)
x

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

y = 3*x+4
y

array([ 4,  7, 10, 13, 16, 19, 22, 25, 28, 31])

用散点图展示这些点

2）使用机器学习模型来拟合这些点

注意：这里传入的训练数据格式需要时一个多纬的数组

from sklearn.linear_model import LinearRegression

#获取模型 训练模型
lr = LinearRegression()
lr.fit(x.reshape(-1,1),y)   #注意这里需要二维数组

3）获取斜率和截距

1、权重/斜率lr.coef_

lr.coef_

array([3.])

2、截距

lr.intercept_

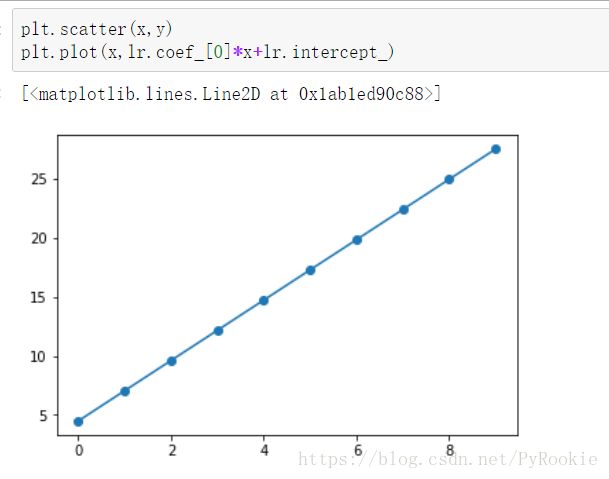
4.000000000000005

4）使用斜率和截距画线

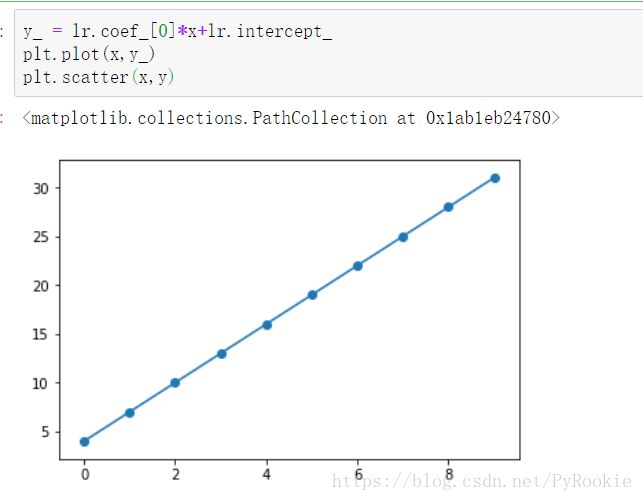
y_ = lr.coef_[0]*x+lr.intercept_ 
plt.plot(x,y_)
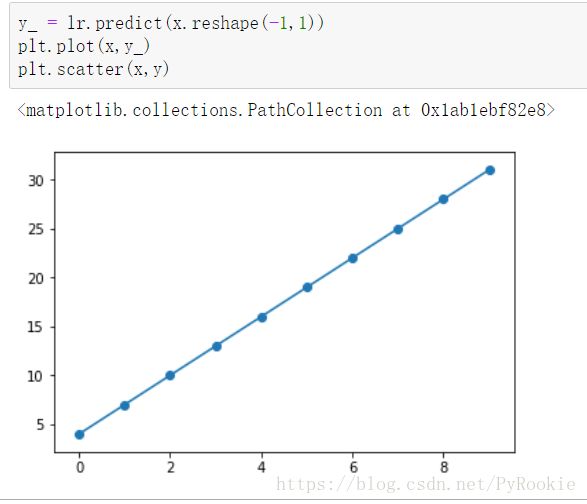
plt.scatter(x,y)

5）使用模型预测数据并画线

注意：这里传入的测试数据格式

y_ = lr.predict(x.reshape(-1,1))

array([ 4.,  7., 10., 13., 16., 19., 22., 25., 28., 31.])

三、测试线性回归的准确性

1）创建测试数据

1、训练集（x，y）

x = np.arange(0,10,1)  # 从0到10 每隔一个取一个
x

#这里先不看w和b的值是什么
w = np.random.random()*10  
b = np.random.random()*5

y = w*x+b
y

array([ 1.89477686,  2.83718029,  3.77958372,  4.72198715,  5.66439058,
        6.60679401,  7.54919744,  8.49160087,  9.4340043 , 10.37640773])

2、画出训练数据的图形

2）线性回归模型

1、创建线性回归模型

lr = LinearRegression()

2、训练线性回归模型

lr.fit(x.reshape(-1,1),y)

3、模型返回权重和截距

lr.coef_ , lr.intercept_

(array([8.86449376]), 1.8902864471553258)

4、画出测试数据的回归曲线

3）对比原数据的权重/截距和预测的权重/截距

lr.coef_ , lr.intercept_
(array([2.55223749]), 4.499348433359231)

w ,b
(2.5522374924290614, 4.499348433359228)

可以看出线性回归预测出来的还是挺准确的。

四、预测糖尿病的严重程度

1）获取数据

1、从sklearn中的datasets获取

# 糖尿病的数据集 是sklearn的datasets里面自带的
import sklearn.datasets as datasets
diabetes = datasets.load_diabetes()
diabetes

2、处理数据

data = diabetes.data # 数据
feature_names = diabetes.feature_names # 特征名
target = diabetes.target # 目标值

2）创建模型并训练模型

lr = LinearRegression()
lr.fit(data,target)  # 传入各个样本的特征 和 结果值

3）获得模型的斜率与截距

1、斜率

w = lr.coef_  # 斜率
w  #这里的样本因为有10个特征，所以有10个斜率，在计算时，使用x 与 w点乘，让样本的每个特征和每个斜率进行计算，加上截距，得出样本值

array([ -10.01219782, -239.81908937,  519.83978679,  324.39042769,
       -792.18416163,  476.74583782,  101.04457032,  177.06417623,
        751.27932109,   67.62538639])

2、截距

b = lr.intercept_  # 截距
b

152.1334841628965

4）随机抽样 预测结果

随机产生一个索引 按照索引从原来的样本中抽取一个数据

看带入模型后算出的结果 和 真实值的偏差

1、产生一个随机样本

在样本范围内随机产生一个索引
再用产生的随机索引在训练数据中取出一个样本和一个目标值

index = np.random.randint(0,442,size=1)[0]
index  #随机索引

data[index] #用随机索引取出一个随机样本
target[index]  # 样本值

2、使用上面训练好的模型预测随机样本

注意：这里的训练模型的斜率是一个元素数量为10的数组
在预测值的时候要将测试样本与斜率点乘。

y_ = np.dot(w,data[index]) + b
# 看看预测出来的结果和真实结果 差别大不大

print('真实的结果是：',target[index])
print('回归的结果是：',y_)

真实的结果是： 293.0
回归的结果是： 199.6971235680727

3、使用预测函数预测测试值

lr.predict(data[index].reshape(1,-1))

array([199.69712357])

5）研究某一特征和糖尿病严重程度的关系并绘图

拿出数据某一列来研究与样本值得关系
研究 bmi 和糖尿病严重程度的关系

1、获取数据

我们将bmi这一列拿出来

bmi_data = data[:,2]

2、处理数据

机器学习的训练数据要求有 样本和特征，从data中拿出来的数据是一个Series。你能给机器模型直接使用。

bmi_data = bmi_data.reshape(-1,1)

3 、训练集

X_train = bmi_data  # 特征
y_train = target  # 目标值

4、创建线性回归模型并训练

创建并训练

lr = LinearRegression()
lr.fit(X_train,y_train)

获得斜率和截距

w = lr.coef_
array([949.43526038])

b = lr.intercept_
152.1334841628967

5、预测出线性回归曲线

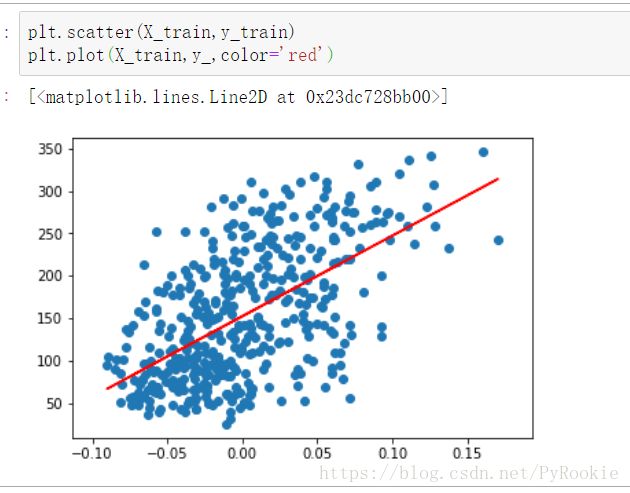
y_ = w*X_train + b
y_

6、画出bmi的线性回归曲线与散点图

plt.scatter(X_train,y_train)
plt.plot(X_train,y_,color='red')

五、矩阵知识

1、阶：方阵的行数（列数）（方阵的行数和列相等）
2、秩：方阵中有用的行的数量
3、 满秩矩阵：秩 = 阶的方阵
4、奇异矩阵：秩 < 阶 的方阵（某些行没用）
5、主对角线：左上角到右下角的对角线
6、单位矩阵：主对角线上是1 其他地方都是0的方阵

六、岭回归

1）岭回归原理

线性回归本质上可以理解为 求各个特征的权重

但是如果特征比样本还多的时候
用线性回归就不能求解了。

比如:
线型回归求这些值可以求出 w
y1 = w1*x1 + w2*x2 + w3*x3
y2 = w1*x1 + w2*x2 + w3*x3
y3 = w1*x1 + w2*x2 + w3*x3

但是观察这些类似于样本的数据:

w1*1 + w2*2 + w3*3 = 10         1   2   3
w1*2 + w2*4 + w3*6 = 20 ==》2   4   6
w1*4 + w2*8 + w3*12 = 40       4   8   12

实际是无法求处w的唯一解的

遇到这种数据时为了求出线性相关，可以给这些数据加一些值造成一点误差。

1    2    3     1    0    0       2    2    3
2    4    6  + 0    1    0  =   2    5    6
4    8    12   0    0    1       4    8    13

这样就可以求类似线性回归的问题了

2）实际使用情况

一般在特征比样本数据多的时候就可以使用岭回归来处理数据。

一般用于图片处理

七、使用岭回归和普通线性回归比较差异

使用糖尿病例子比较岭回归和普通线性回归

1）导入数据

import sklearn.datasets as datasets
diabetes = datasets.fetch_mldata
diabetes
data = diabetes.data
target = diabetes.target

2）创建岭回归训练模型并训练

rr = Ridge(alpha=10)
alpha： 岭回归缩减系数
默认为 1
如果参数alpha的值为0 的话，各个特征的权重与普通线性回归一样了。

如果偏差太大，各个特征的权重就几乎为0了。
一般在图像处理的时候

from sklearn.linear_model import Ridge
rr = Ridge(alpha=100)  #alpha 引入的误差大小，alpha值越大，误差越大

rr.fit(data,target) #模型训练

3）查看岭回归模型的斜率与截距

rr.coef_

array([ 0.03040324,  0.00695983,  0.09491727,  0.07145177,  0.03430439,
        0.02815743, -0.06389202,  0.06965804,  0.09158435,  0.0618977 ])

rr.intercept_

152.1334841628965

4）创建普通线性回归模型并训练

from sklearn.linear_model import LinearRegression

lr = LinearRegression()  #创建模型

lr.fit(data,target)   #训练模型

5）查看普通线性回归的斜率与截距

lr.coef_

array([ -10.01219782, -239.81908937,  519.83978679,  324.39042769,
       -792.18416163,  476.74583782,  101.04457032,  177.06417623,
        751.27932109,   67.62538639])

lr.intercept_

152.1334841628965

八、深入研究岭回归（岭际线）

Ridge(alpha=1)
不同的alpha对的值对模型权重的影响

1）创建数据

np.arange(1,10,1).reshape(-1,1)

array([[1],
       [2],
       [3],
       [4],
       [5],
       [6],
       [7],
       [8],
       [9]])

np.arange(0,10,1)

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

将上面两个加起来

np.arange(1,10,1).reshape(-1,1)+np.arange(0,10,1)

array([[ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10],
       [ 2,  3,  4,  5,  6,  7,  8,  9, 10, 11],
       [ 3,  4,  5,  6,  7,  8,  9, 10, 11, 12],
       [ 4,  5,  6,  7,  8,  9, 10, 11, 12, 13],
       [ 5,  6,  7,  8,  9, 10, 11, 12, 13, 14],
       [ 6,  7,  8,  9, 10, 11, 12, 13, 14, 15],
       [ 7,  8,  9, 10, 11, 12, 13, 14, 15, 16],
       [ 8,  9, 10, 11, 12, 13, 14, 15, 16, 17],
       [ 9, 10, 11, 12, 13, 14, 15, 16, 17, 18]])

再1除以这个数据中的每个元素
作为测试集

X = 1/(np.arange(1,10,1).reshape(-1,1)+np.arange(0,10,1))  # 里面都是0到1的数据
X

array([[1.        , 0.5       , 0.33333333, 0.25      , 0.2       ,
        0.16666667, 0.14285714, 0.125     , 0.11111111, 0.1       ],
       [0.5       , 0.33333333, 0.25      , 0.2       , 0.16666667,
        0.14285714, 0.125     , 0.11111111, 0.1       , 0.09090909],
       [0.33333333, 0.25      , 0.2       , 0.16666667, 0.14285714,
        0.125     , 0.11111111, 0.1       , 0.09090909, 0.08333333],
       [0.25      , 0.2       , 0.16666667, 0.14285714, 0.125     ,
        0.11111111, 0.1       , 0.09090909, 0.08333333, 0.07692308],
       [0.2       , 0.16666667, 0.14285714, 0.125     , 0.11111111,
        0.1       , 0.09090909, 0.08333333, 0.07692308, 0.07142857],
       [0.16666667, 0.14285714, 0.125     , 0.11111111, 0.1       ,
        0.09090909, 0.08333333, 0.07692308, 0.07142857, 0.06666667],
       [0.14285714, 0.125     , 0.11111111, 0.1       , 0.09090909,
        0.08333333, 0.07692308, 0.07142857, 0.06666667, 0.0625    ],
       [0.125     , 0.11111111, 0.1       , 0.09090909, 0.08333333,
        0.07692308, 0.07142857, 0.06666667, 0.0625    , 0.05882353],
       [0.11111111, 0.1       , 0.09090909, 0.08333333, 0.07692308,
        0.07142857, 0.06666667, 0.0625    , 0.05882353, 0.05555556]])

X.shape
(9, 10)    #这是一个9 行10 列的矩阵
# 这个X就是测试集

结果集

y = np.ones(9)
y

array([1., 1., 1., 1., 1., 1., 1., 1., 1.])

2）创建线性回归模型并训练数据

lr = LinearRegression()
lr.fit(X,y)

3）查看斜率和截距

lr.coef_

array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])   

这里可以看出使用线性回归处理特征数量大于样本数量的数据时，权重都为0。找到的特征和结果无关！

lr.intercept_

1.0

4）创建岭回归模型并训练数据

1、通过修改Ridge(fit_intercept=False)

来让岭回归模型来关闭差值，不让差值调整结果值
这样我们获得的斜率就不是0了。

rr = Ridge(fit_intercept=False)
rr.fit(X,y)

5）查看斜率和截距

rr.coef_

array([0.50338083, 0.4975694 , 0.44988445, 0.40522804, 0.36730309,
       0.33543542, 0.3084947 , 0.2854958 , 0.2656627 , 0.24839685])

rr.intercept_

0.0

6）创建一个alpha集合

用以验证种不同alpha值对预测数据的结果的影响

1、np.logspace（）

np.logspace(1,3,3)  #从1-3分为三个 1 2 3 分别
# 1**10   2**10   3**10 
array([  10.,  100., 1000.])

2、创建alpha集合

一般alpha的范围取 -1000,200之间，太大会影响结果值

alphas = np.logspace(-10,2,100)  # -10 到 2 取100份
alphas 

array([1.00000000e-10, 1.32194115e-10, 1.74752840e-10, 2.31012970e-10,
       3.05385551e-10, 4.03701726e-10, 5.33669923e-10, 7.05480231e-10,
       9.32603347e-10, 1.23284674e-09, 1.62975083e-09, 2.15443469e-09,
     。。。
       1.51991108e+00, 2.00923300e+00, 2.65608778e+00, 3.51119173e+00,
       4.64158883e+00, 6.13590727e+00, 8.11130831e+00, 1.07226722e+01,
       1.41747416e+01, 1.87381742e+01, 2.47707636e+01, 3.27454916e+01,
       4.32876128e+01, 5.72236766e+01, 7.56463328e+01, 1.00000000e+02])

7）创建岭回归机器学习算法对象

创建很多的 模型 分别设置不同的 alpha 观察变化

coefs = []
for alpha in alphas:
    # 获取模型 设置参数
    rr = Ridge(alpha=alpha,fit_intercept=False)
    rr.fit(X,y)
    coefs.append(rr.coef_)

8）绘图查看alpha参数和coefs的关系

plt.figure(figsize=(12,8))  #设置画布大小
plt.plot(alphas,coefs)  #绘图
# 设置坐标轴 不是以均匀的方式展示 设置x轴线 而是 以10的倍数来显示
plt.xscale('log')

通过观察 岭际线 发现
大于10的-3次方 各个特征的权重就几乎为0了
小于10的-7次方 某些特征的权重的变化幅度就会非常大 很容易出问题
比较保守的猜测 我们在 10的-7次方 到 10的-3次方 之间 取一个alpha值比较合适

九、lasso回归

1）原理解释

1、最小绝对值收缩和选择算子

2、通俗解释

线性回归时使 权重的绝对值相加 让其结果不能大于某个值

一般在特征很多的时候，很多特征对结果的影响几乎为0，我们就可以限制 拉姆达的值，让加和小于某个值，其中权重最小的就会被归零，加和的值还大于拉姆达的话，再让最小的归零，知道小于拉姆达为止。

十、普通线性回归、岭回归与lasso回归比较

1）创建数据

1、随机生成数据集

np.random.seed(10)  # 给随机数一个种子，他就不会再产生其他的随机数了。
samples = 50  # 有几个样本就有几行
features = 100  # 有几个特征就有几列
X = np.random.randn(samples,features)  # 以0为中心，标准差为1的数 参数为形状
# X 作为特征值

2、随机生成权重

w = 10*np.random.randn(features)  # 有几个特征就有几个权重的值  给每个权重扩大10倍
w

2）模拟lasso的效果，将一些权重归零

通过打乱权重的索引，打乱权重的值
然后再通过打乱的索引，取前90个
然后再在原来的权重值中，将随机索引的前90个对应的w值归零，这样就随机归零了90个权重

index = np.random.permutation(features)  # 打乱的 各个权重的索引

index[:90]  # 找出前九十个索引

w[index[:90]] = 0  # 把前九十个打乱顺序的所对应的权重值 归零

3）根据现有的特征值与权重值求目标值

# 各个样本的特征 X
# 各个特征的权重是 w
y = np.dot(X,w)
y

4）比较各回归方式 预测权重的效果

1、导入模型

from sklearn.linear_model import LinearRegression,Ridge,Lasso

2、创建模型

lr = LinearRegression()
rr = Ridge(alpha=1,fit_intercept=False)  #这里主要研究 w 的值，所以为了不受影响，不使用偏差值
lasso = Lasso(alpha=0.8)  #alpha 用来设置权重的上限，不过alpha 的值为0-1的小数 用来表示有用的特征的比例

注意：Lasso中的alpha 表示有用特征的比例
例如 共有 5 个特征， 有用的 只有一个，那么 alpha = 0.2

3、 训练数据

lr.fit(X,y)
rr.fit(X,y)
lasso.fit(X,y)

5）查看各个模型对coef的预测是否正确

1、使用画布将真实的、普通线性回归、岭回归、lasso回归 这四个画出来。

plt.figure(figsize=(12,8))  #设置画布大小
axes1 = plt.subplot(2,2,1)  # 先绘制真实的权重
axes1.plot(w)
axes1.set_title('real')
# 普通线性回归
axes2 = plt.subplot(2,2,2)
axes2.plot(lr.coef_)
axes2.set_title('lr')
# 岭回归
axes3 = plt.subplot(2,2,3)
axes3.plot(rr.coef_)
axes3.set_title('rr')
# 拉索回归
axes4 = plt.subplot(2,2,4)
axes4.plot(lasso.coef_)
axes4.set_title('lasso')