Python高级--支持向量机SVM

一、支持向量机原理

1）支持向量机基本概念

Support Vector Machine

支持向量机，其含义是通过支持向量运算的分类器。
其中“机”的意思是机器，可以理解为分类器。 那么什么是支持向量呢？在求解的过程中，会发现只根据部分数据就可以确定分类器，这些数据称为支持向量。

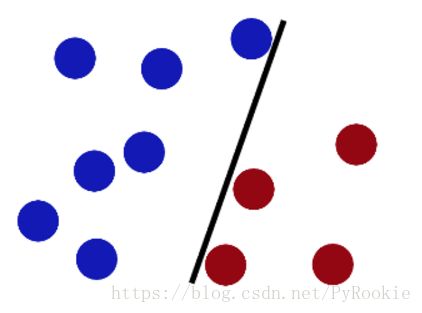
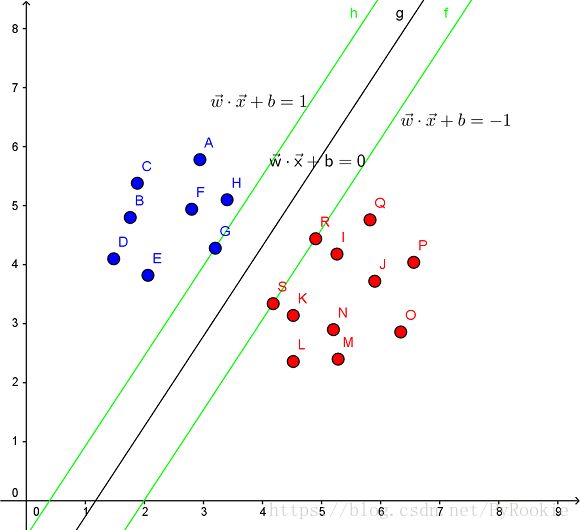
见下图，在一个二维环境中，其中点R，S，G点和其它靠近中间黑线的点可以看作为支持向量，它们可以决定分类器，也就是黑线的具体参数。

2）举例说明

在很久以前的七夕，大侠要去救他的女神，但魔鬼和他玩了一个游戏。

魔鬼在桌子上似乎有规律放了两种颜色的球，说：“你能不能分开它们？要求：尽量在放更多球之后，仍然适用。”

于是大侠这样放，干的不错？

然后魔鬼，又在桌上放了更多的球，似乎有一个球站错了阵营

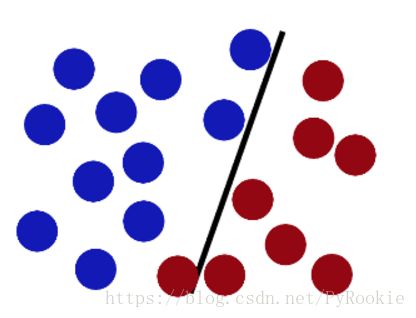
SVM就是试图把棍放在最佳位置，好让在棍的两边有尽可能大的间隙

现在即使魔鬼放了更多的球，棍仍然是一个好的分界线

魔鬼看到大侠已经学会了一个trick，于是魔鬼给了大侠一个新的挑战

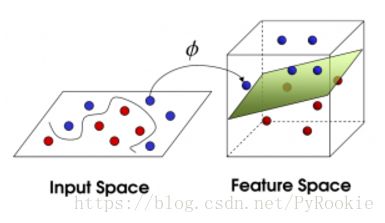
现在，大侠没有棍可以很好帮他分开两种球了，现在怎么办呢？当然像所有武侠片中一样大侠桌子一拍，球飞到空中。然后，凭借大侠的轻功，大侠抓起一张纸，插到了两种球的中间

现在，从魔鬼的角度看这些球，这些球看起来像是被一条曲线分开了

愚蠢的人类，把球叫做 「data」
把棍子叫做 「classifier」
最大间隙的技巧叫做「optimization (最优化)」
几种划分方式叫做「kernelling内核」
那张纸叫做「hyperplane超平面」

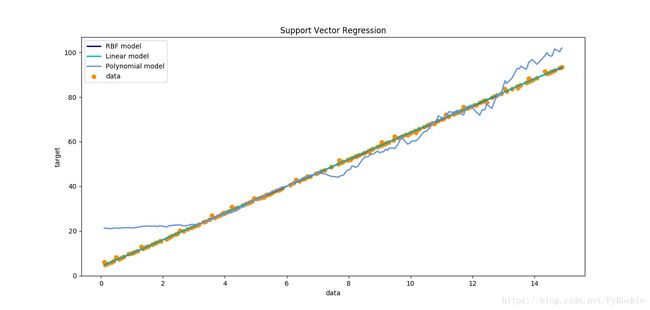
3）三种内核的效果比较

1、Linear核

线性函数
其实就是画直线（一次方）

主要用于线性可分的情形。参数少，速度快，适用于一般数据

2、RBF核

径向基函数 (Radial Basis Function 简称 RBF)
基于半径的函数
其实就是画曲线（二次方）

主要用于线性不可分的情形。参数多，分类结果非常依赖于参数的情况。

3、polynomial model

参数较多，在另外两种都不适用的时候选择
（多项式 n次方）（一般来说什么都画不好）

4）优缺点

1、论效果

svm不像knn那样容易过拟合 有很好的泛化能力
svm是找两类之间的最大距离 所以不像线性回归那样容易欠拟合

2、论效果

论效率 svm和knn一样，每个点都要计算距离，计算量比较大，所以一般针对小样本数据

3、总结

总结： SVM是一种主要针对小样本数据进行学习、分类和回归的方法

二、使用SVM画出决策边界

对两堆数据进行分类，并画出

import numpy as np
import pandas as pd
from pandas import Series,DataFrame
import matplotlib.pyplot as plt

支持向量机导包

from sklearn.svm import SVC

1）创造数据

产生两堆数据 20个样本，每个样本有两个特征

## 以0为中心 标准差是1的 一堆正太分布的数据
# 分开两堆数据的中心
dot1 = np.random.randn(20,2)-[1,4]  # 将中心向左下移动
dot2 = np.random.randn(20,2)+[2,3]  # 将中心向 右上移动

将产生的数据绘制查看

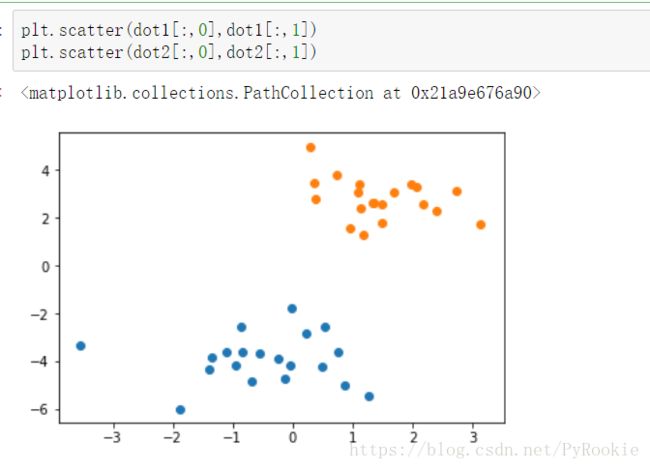
plt.scatter(dot1[:,0],dot1[:,1])
plt.scatter(dot2[:,0],dot2[:,1])

2）合并数据作为训练集并创建目标值

X_train = np.concatenate((dot1,dot2))

# dot1的目标值是0 dot2的目标值是1
# 则y_train中前面20个是0 后面20个是1
y_train = [0]*20 + [1]*20

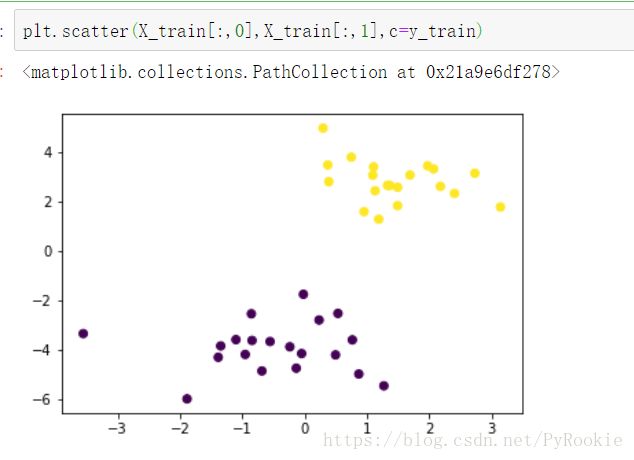
根据训练集和目标值绘图

plt.scatter(X_train[:,0],X_train[:,1],c=y_train)

3）使用内核为linear的支持向量机模型绘制超平面分隔线

1、创建内核为linear的模型并训练

svc = SVC(kernel='linear')
svc.fit(X_train,y_train)

4）超平面

f(x) = w*x + b

1、提取系数获取分隔线斜率

svc.coef_

array([[0.22671513, 0.56914011]])

这两个分别是两个特征的权重，但这并不是我们想要的
第一个权重：w0 是 y_train/X_train[:,0]
第二个权重：w1 是 y_train/X_train[:,1]

现在要求的是将x0作为横轴，x1作为纵轴
这条线的斜率为 x1 / x0
w = w1 / w0
w = y_train/X_train[:,1] / y_train/X_train[:,0]

svc.coef_
svc.coef_[0,0]
svc.coef_[0,1]
w = -svc.coef_[0,0]/svc.coef_[0,1]

2、提取系数获取分隔线截距

svc.intercept_ 

array([0.00599865])

这里的截距是目标值上面的截距，但是我们现在要找的是x1上的截距
X_train[:,1]和y_train的 斜率是 w1 svc.coef_[0,1]
w1已知 在y_train上的截距也是已知的 求在X_train[:,1]上的截距
svc.intercept_/-??? = svc.coef_[0,1]
??? = -svc.intercept_/svc.coef_[0,1]
求出这条分隔线的斜率

b = -svc.intercept_[0]/svc.coef_[0,1]

-0.010539844074062357

5）画出这条分割线

1、创建分割线的x值

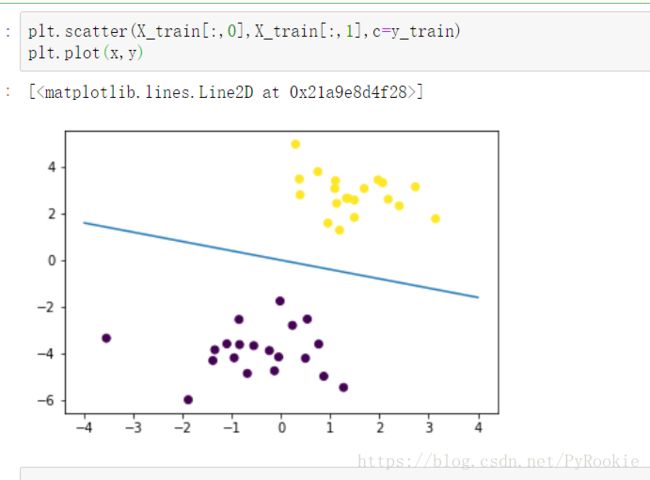
x = np.linspace(-4,4,100)

2、算出分割线的y值并绘图显示

y = w*x+b

plt.scatter(X_train[:,0],X_train[:,1],c=y_train)
plt.plot(x,y)

6）支持向量

使用svc.support_vectors_找出支持向量，即离分割线最近的点集合，绘制出支持向量的所有点

1、找出支持向量的点

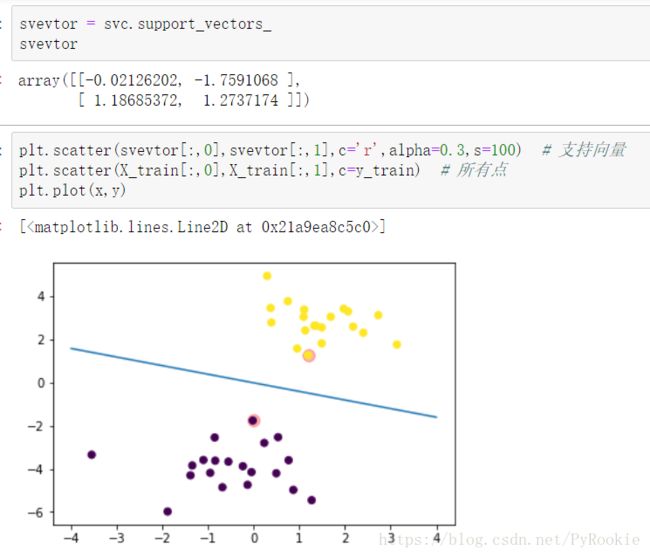
svevtor = svc.support_vectors_
svevtor

array([[-0.02126202, -1.7591068 ],
       [ 1.18685372,  1.2737174 ]])

2、绘制出支持向量的点

plt.scatter(svevtor[:,0],svevtor[:,1],c='r',alpha=0.3,s=100)  # 支持向量
plt.scatter(X_train[:,0],X_train[:,1],c=y_train)  # 所有点
plt.plot(x,y)

7）绘制经过两个支持向量的点

已知 斜率 和 经过的点 画线
把两个直线的 b求出来 即可 b1 b2

# 第一个支持向量点
p1 = svevtor[0]
p1
#
p2 = svevtor[1]
p2
#已知k，x，y 求b
y = k*x+b
b = y-k*x

b1 = p1[1]-w*p1[0]
b1

b2 = p2[1]-w*p2[0]
b2

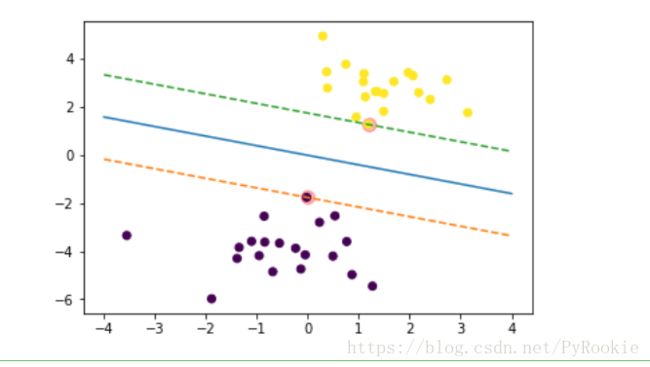
求出y1 y2 画出两条经过支持向量的线

y1 = w*x+b1
y2 = w*x+b2

plt.scatter(svevtor[:,0],svevtor[:,1],c='r',alpha=0.3,s=100)  # 支持向量
plt.scatter(X_train[:,0],X_train[:,1],c=y_train)  # 所有点
plt.plot(x,y)  # 分类的中心线
# 分类的上边界 和 下边界
plt.plot(x,y1,ls='--')
plt.plot(x,y2,ls='--')

三、使用多种核函数对iris数据进行分类

1）导包

from sklearn.svm import SVC 

2）数据获取

只提取两个特征，方便画图

from sklearn.datasets import load_iris
iris = load_iris()
data = iris.data[:,:2]
target = iris.target

3）创建模型并训练

l = SVC(kernel='linear')
r = SVC(kernel='rbf')  # 二次曲线
p = SVC(kernel='poly')  # 高次曲线

l.fit(data,target)
r.fit(data,target)
p.fit(data,target)

4）创建测试集

我们取画布上的所有点进行测试

x = np.linspace(data[:,0].min(),data[:,0].max(),200)
y = np.linspace(data[:,1].min(),data[:,1].max(),200)

xx,yy =np.meshgrid(x,y)

X_test = np.c_[xx.flatten(),yy.flatten()]

5）预测并绘图

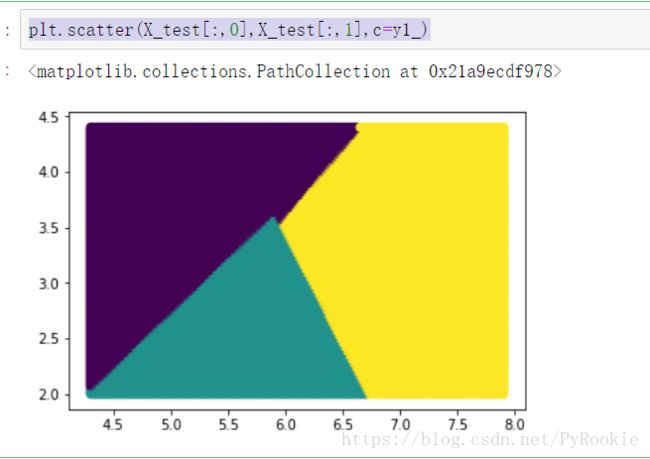
1、用linear内核做预测

y1_ = l.predict(X_test)  # 用linear内核做预测
plt.scatter(X_test[:,0],X_test[:,1],c=y1_)

2、用rbf内核做预测

y2_ = r.predict(X_test)  # 用rbf内核做预测
plt.scatter(X_test[:,0],X_test[:,1],c=y2_)

3、用poly内核做预测

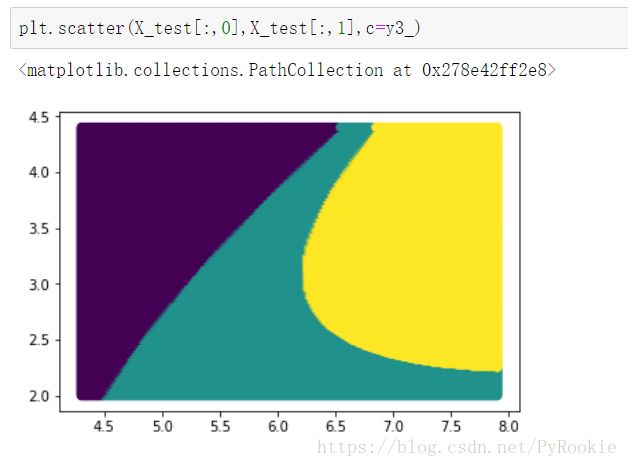
y3_ = p.predict(X_test)  # 用poly内核做预测
plt.scatter(X_test[:,0],X_test[:,1],c=y3_)

四、使用SVM多种核函数进行回归

1）导包

from sklearn.svm import SVR 

2）创建样本点并生成sin曲线

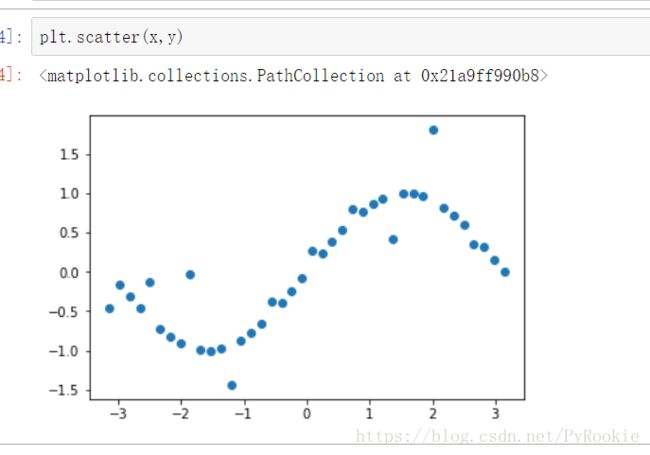
x = np.linspace(-np.pi,np.pi,40)
y = np.sin(x)

plt.scatter(x,y)

3）数据加噪

每隔四个添加一个噪声

noise = np.random.random(10) - 0.5  # [-0.5, 0.5)
y[::4]+=noise

4）建立SVR模型并训练数据

# 获取模型
l = SVR(kernel='linear')
r = SVR(kernel='rbf')
p = SVR(kernel='poly')

# 训练模型
l.fit(x.reshape(-1,1),y)
r.fit(x.reshape(-1,1),y)
p.fit(x.reshape(-1,1),y)

5）创建测试数据并分别预测

# 生成一些测试的X_test
X_test = np.linspace(-np.pi,np.pi,15).reshape(-1,1)

y1_ = l.predict(X_test)
y2_ = r.predict(X_test)
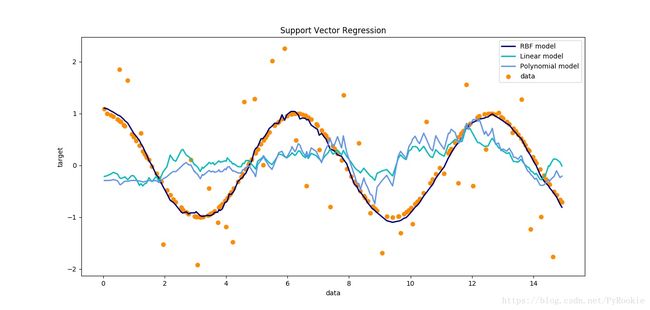
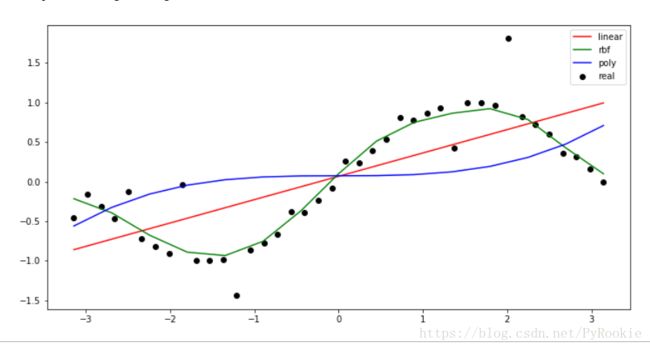
y3_ = p.predict(X_test)

6）绘制比较三种不同内核的回归效果

plt.figure(figsize=(12,6))
plt.scatter(x,y,c='k',label='real')  # 真实数据
plt.plot(X_test,y1_,c='r',label='linear')  # linear内核
plt.plot(X_test,y2_,c='g',label='rbf')   # 二次曲线
plt.plot(X_test,y3_,c='b',label='poly')   # 高次曲线
plt.legend()  #显示图例

由图像可以观察得出rbf 对于曲线效果是最好的。