动手学深度学习(tensorflow)---学习笔记整理（五、过拟合和欠拟合相关问题篇）

有关公式、基本理论等大量内容摘自《动手学深度学习》(TF2.0版)）

什么是过拟合和欠拟合？

在我们训练模型过程中经常会遇见两个问题：我们的模型训练过程中准确率很高，但是实际应用或者使用验证集的时候效果比较差；我们模型训练过程准确率比较低，一直无法得到高的准确率。我们通常把前者称为过拟合，后者称为欠拟合。

通俗的说就是：以考研为例，我们希望考生模拟题做的好，考场上也能发挥出对应水平来。

过拟合就是一个人天天做考研模拟试卷（训练集），这些试卷基本上都是满分（准确率很高），但是真正上考场了考的分数很低（实际应用/验证集效果很差）。

欠拟合就更容易理解了，模拟卷都一直做不对...考试的时候也一样。、

总是上述模型都没有学习好，一个仅仅只适用于训练集，另一个则训练集都没学会。

那么上述两个情况为什么会发生呐？一方面有数据集决定，另一方面由模型决定。

从经验上来说：数据集越大，模型能学习的训练集越多就更容易发现其特征，更容易学好；模型越复杂也往往越容易学习更多的特征（等等会以三次多项式项和一次项来举例）

演示过拟合、欠拟合图像的代码如下：

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
#生成数据集
n_train, n_test, true_w, true_b = 100, 100, [1.2, -3.4, 5.6], 5
#随机一维x值
features = tf.random.normal(shape=(n_train + n_test, 1))
#映射的三维x值
poly_features = tf.concat([features, tf.pow(features, 2), tf.pow(features, 3)],1)
print(poly_features.shape)
labels = (true_w[0] * poly_features[:, 0] + true_w[1] * poly_features[:, 1]+ true_w[2] * poly_features[:, 2] + true_b)
print(tf.shape(labels))
labels += tf.random.normal(labels.shape,0,0.1)
#绘图相关函数
from IPython import display
def use_svg_display():
    display.set_matplotlib_formats('svg')

def set_figsize(figsize=(3.5, 2.5)):
    """Set matplotlib figure size."""
    use_svg_display()
    plt.rcParams['figure.figsize'] = figsize
def semilogy(x_vals, y_vals, x_label, y_label, x2_vals=None, y2_vals=None,
             legend=None, figsize=(3.5, 2.5)):
    set_figsize(figsize)
    plt.xlabel(x_label)
    plt.ylabel(y_label)
    plt.semilogy(x_vals, y_vals)
    if x2_vals and y2_vals:
        plt.semilogy(x2_vals, y2_vals, linestyle=':')
        plt.legend(legend)
    plt.show()
#训练+绘制
num_epochs, loss = 100, tf.losses.MeanSquaredError()
def fit_and_plot(train_features, test_features, train_labels, test_labels):
    net = tf.keras.Sequential()
    net.add(tf.keras.layers.Dense(1))
    batch_size = min(10, train_labels.shape[0])
    train_iter = tf.data.Dataset.from_tensor_slices(
        (train_features, train_labels)).batch(batch_size)
    test_iter = tf.data.Dataset.from_tensor_slices(
        (test_features, test_labels)).batch(batch_size)
    optimizer = tf.keras.optimizers.SGD(learning_rate=0.01)
    train_ls, test_ls = [], []
    for _ in range(num_epochs):
        for X, y in train_iter:
            with tf.GradientTape() as tape:
                l = loss(y, net(X))

            grads = tape.gradient(l, net.trainable_variables)
            optimizer.apply_gradients(zip(grads, net.trainable_variables))

        train_ls.append(loss(train_labels, net(train_features)).numpy().mean())
        test_ls.append(loss(test_labels, net(test_features)).numpy().mean())
    print('final epoch: train loss', train_ls[-1], 'test loss', test_ls[-1])
    semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'loss',
             range(1, num_epochs + 1), test_ls, ['train', 'test'])
    print('weight:', net.get_weights()[0],
          '\nbias:', net.get_weights()[1])
#三阶多项式函数拟合
fit_and_plot(poly_features[:n_train, :], poly_features[n_train:, :],
             labels[:n_train], labels[n_train:])
#线性函数拟合
fit_and_plot(features[:n_train, :], features[n_train:, :], labels[:n_train],
             labels[n_train:])
#少量数据训练
fit_and_plot(poly_features[0:2, :], poly_features[n_train:, :], labels[0:2],
             labels[n_train:])

上述代码进行了做了三次多项式回归正常样例、一次线性回归正常样例、三次多项式回归极少样例的对比实验。

实验结果如下：

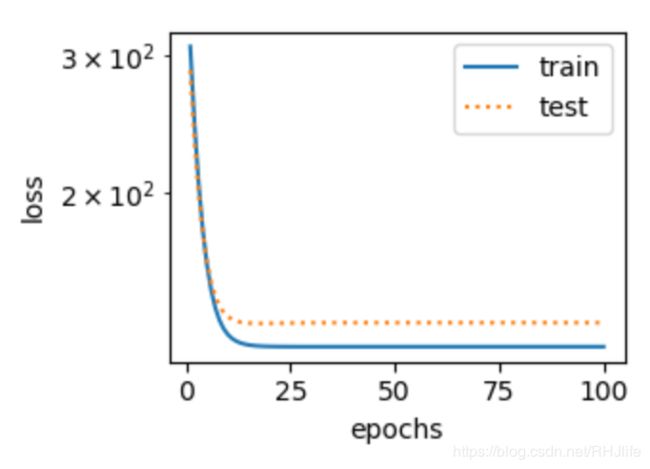
三次多项式回归正常样例：（正常）

 

一次线性回归正常样例：（过拟合）

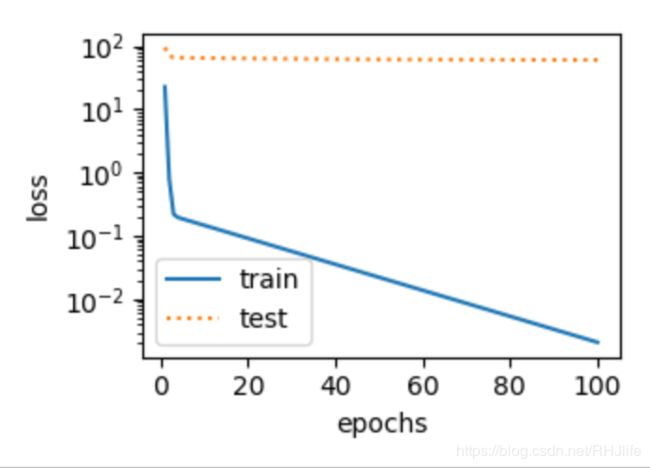
三次多项式回归极少样例：（欠拟合）

为什么会出现这种现象呐？

样例二的原因是，模型过于简单，即使有丰富的样例，但是他是个线性模型只认为有一个W，无法学会三次多项式的三个W，所以出现了过拟合；样例三的原因是，通俗点说，就是给的太少，模型学不到太多东西。

世界上也没有绝对准确的函数，往往在过拟合和欠拟合之间寻找一个最佳的。

一些防止过拟合和欠拟合的方法

K折交叉验证

通过上述我们可以知道，训练样本越多越好，如果我们的数据样本很少的时候，我们划分训练集和训练集的时候（例如8:2），会感觉给数据集中只有8成用来训练数据感觉有点可惜（我们肯定想把全部数据都给训练～），那么人们提出了一种划分方案，即K折交叉验证。其实现方法即：把数据集划分为10分，第一轮训练的时候把前九份当成训练集，第十份当成验证集，第二轮训练的时候选择第九份数据当验证集，其他的当训练集，第三轮训练选择第八份当成验证集...通过上述思想，所有的数据都会进行训练，也都会进行验证。

权重衰减/ L2范数正则化

虽然增大训练数据集可能会减轻过拟合，但是获取额外的训练数据往往代价高昂。所以我们学习一个新的防治过拟合的算法。

下面介绍下L2犯数正则化：

线性回归的优化算法：

综上所述：L2范式正则化即增加了惩罚项，该惩罚项与w有关，所以优化过程中求导也会产生新的求导项，最终化简为图中公式。

丢弃法

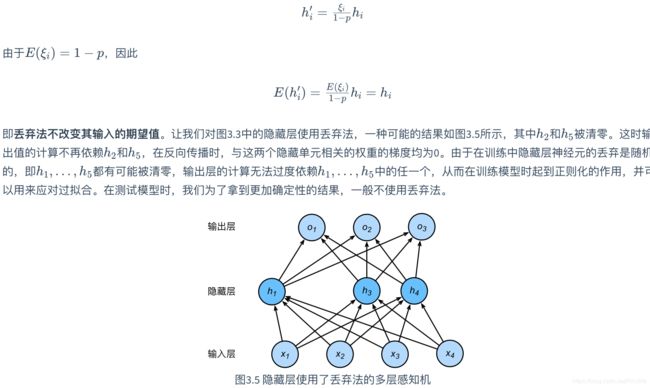
除了前面介绍的权重衰减，深度学习模型常常使用丢弃法来缓解过拟合问题。丢弃法有一些不同的变体。本节中提到的丢弃法特指倒置丢弃法

说白了就是，训练的时候随机丢弃某些神经元，但是预测的时候不丢弃。

丢弃法从零实现

import tensorflow as tf
import numpy as np
from tensorflow import keras, nn, losses
from tensorflow.keras.layers import Dropout, Flatten, Dense

def dropout(X, drop_prob):
    assert 0 <= drop_prob <= 1
    keep_prob = 1 - drop_prob
    # 这种情况下把全部元素都丢弃
    if keep_prob == 0:
        return tf.zeros_like(X)
    #初始mask为一个bool型数组，故需要强制类型转换
    #mask为一个随机矩阵,tf.random.uniform生成shape形状介于minval和maxval之间均匀分布随机数
    #

丢弃法简单实现

import tensorflow as tf
from tensorflow import keras, nn, losses
from tensorflow.keras.layers import Dropout, Flatten, Dense
from tensorflow.keras.datasets import fashion_mnist
#导入数据集
batch_size=256
(x_train, y_train), (x_test, y_test) = fashion_mnist.load_data()
x_train = tf.cast(x_train, tf.float32) / 255 #在进行矩阵相乘时需要float型，故强制类型转换为float型
x_test = tf.cast(x_test,tf.float32) / 255 #在进行矩阵相乘时需要float型，故强制类型转换为float型
train_iter = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(batch_size)
test_iter = tf.data.Dataset.from_tensor_slices((x_test, y_test)).batch(batch_size)
#定义模型
model = keras.Sequential([
    keras.layers.Flatten(input_shape=(28, 28)),
    keras.layers.Dense(256,activation='relu'),
    Dropout(0.2),
    keras.layers.Dense(256,activation='relu'),
    Dropout(0.5),
    keras.layers.Dense(10,activation=tf.nn.softmax)
])
#配置模型参数
model.compile(optimizer=tf.keras.optimizers.Adam(),
              loss = 'sparse_categorical_crossentropy',
              metrics=['accuracy'])
#模型训练
model.fit(x_train,y_train,epochs=5,batch_size=256,validation_data=(x_test, y_test),
                    validation_freq=1)