哈夫曼树的建立
设计题目:
一、设计实验条件
DevC++
二、设计任务及要求
1. 建立最优二叉树函数;
2. 建立函数输入二叉树,并输出其赫夫曼树;
3. 分析算法的时间复杂度,进行优化。
三、设计报告的内容
1. 设计题目与设计任务
设计题目:建立赫夫曼树。
设计任务:建立最优二叉树函数,并输出其赫夫曼树。实现赫夫曼树存储结构的初始化,建立赫夫曼树并打印。在此基础上对算法的时间复杂度进行分析并进行优化。
2. 前言(绪论)
在很多问题的处理过程中,需要进行大量的条件判断,这些判断结构的设计直接影响着程序的执行效率。因此,我们需要寻找一种最佳判定树,即赫夫曼树,来高效地存储、处理数据。本课程设计主要进行赫夫曼树的建立,通过此设计充分理解赫夫曼树的原理,同时也为赫夫曼编码奠定基础。
赫夫曼树的建立是赫夫曼编码的前提,赫夫曼编码可以起到数据压缩的作用,提高程序的执行效率。
3. 设计主体
3.1需求分析
1.任务:
本程序主要通过用户输入二叉树各个节点的权值,然后输出赫夫曼树。
2.功能模块:
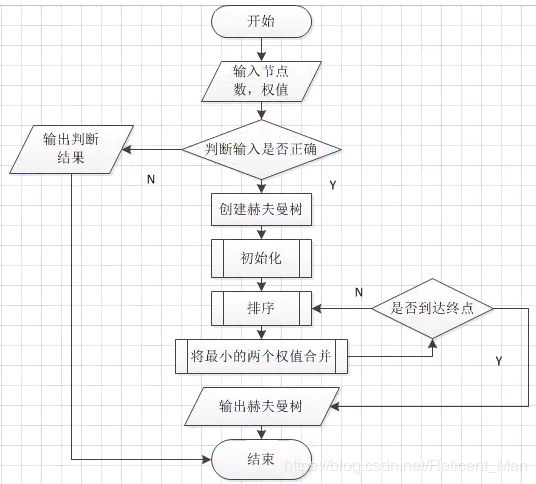
3.流程图:
4.输入输出
输入形式:数字(整数)
输入范围:节点数:1到20;权值:int范围
输出形式:数字,括号,逗号。
5.功能:
输出赫夫曼树,能够显示每个节点的左子树,右子树。
6.测试数据:
3.2系统设计
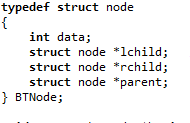
1.数据的定义:
结构体的定义:
结构体类型指针及数组的定义:
2.基本操作及伪码算法:
①初始化结构体数组
②快速排序
③选择权值最小的两个合并
④赫夫曼树的遍历
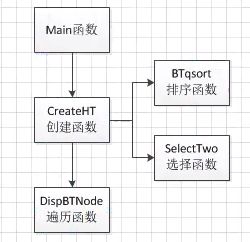
3.函数调用图
4.主程序
3.3系统实现
1.基础算法:
① 将所有左,右子树都为空的作为根节点;
② 在森林中选出两根节点的权值最小的树作为一棵树的左,右子树,且置新树的附加根节点的权值为其左,右子树上根节点的权值之和,其中左子数的权值小于右子树的权值;
③ 从森林中删除这两颗树,同时把新树加入到森林中;
④ 重复②,③步骤,直到森林中只有一棵树为止,此树便是赫夫曼树。
2.问题分析及解决:
在掌握算法原理后,我着手实践。因为最后的赫夫曼树有2n-1个节点,于是我开一个大小为2n-1的结构体类型的数组存储权值,其中前n个空间用来存储排序好的原来的二叉树的权值,后n-1个存储空间用来存储每次选出的两个最小的权值之和,在测试了几组数据后发现有的结果出错,经过分析发现,判定过最小的权值后,在下一次选取最小值时进行了重复判断,对结果产生了干扰。于是我另外设定了一个数组判断是否在之前已经判断过,终于解决了问题。
后来发现纯数字的输出形式看不出子树与双亲之间的对应关系。翻阅数据结构书时,看到广义表,于是我想到用加括号的方法,即先判断一个节点是否有左子树(在赫夫曼树中有左子树就一定有右子树),如果有就输出括号,左右子树之间用逗号相隔。这样便增加了直观可读性。
3.回顾与分析:
本课程设计主要采用结构体类型指针、各函数相互调用的框架,实现了赫夫曼树的建立,其中对纯数字进行建立赫夫曼树,在实际应用中可能需要进行字符替换,在这一方面需要改进。通过程序的实现,进一步加深了对赫夫曼编码的理解。
4.算法的时空分析及改进
在进行排序操作时,若采用冒泡排序的方法,时间复杂度为O(n^2),空间复杂度为O(n),优点是简单易行,代码量少,缺点为运行速度慢。
改进为快速排序,采用递归的方法,时间复杂度可降为O(nlogn),空间复杂度可降为O(logn)。优点是显著的提高了运算效率,缺点是快排不稳定,对于一些特殊的问题不适用。
3.4用户手册
1.运行程序;
2.输入节点数;
3.输入各个节点的权值;
4.观察运行结果;
5.结束。
3.5测试
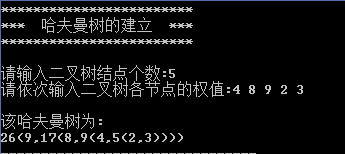
1.运行程序;
2.输入节点数5;
3.输入权值4 8 9 2 3;
4.运行结果:
5.结束。
4. 结束语
本次课程设计完成了赫夫曼树的建立,直观的显示出各子树与双亲的关系,有效地提高了执行效率.赫夫曼树的建立为其编码奠定基础,将来可以用于数据的压缩处理。
5. 参考资料
[1] 严蔚敏,吴伟民,《数据结构》(C语言版),清华大学出版社,2007
[2] 谭浩强,《C++程序设计》,清华大学出版社,2015
[3] Stanley B.LippmanBarbara E.Moo JoseeLaJolie,《C++ Primer》,人民邮电出版社, 2006
[4] KennethA.Reek,《C和指针》,人民邮电出版社,2008
[5] 博客,http://www.cnblogs.com/mcgrady/p/3329825.html
[6] 张颖江,胡燕,《C语言程序设计》,科学出版社,1998
6. 附录
#include
#include
#define N 20
using namespace std;
int p[100]={0}; //用来判断节点是否 被选取过
typedef struct node //建立哈夫曼树的结构体
{
int data;
struct node *lchild; //定义各节点
struct node *rchild;
struct node *parent;
} BTNode;
void BTqsort(BTNode *ht,int low,int high) //快排
{
if(low>=high-1)
return ; //结束
int key=ht[low].data; //记录枢轴
int i=low;
int j=high-1;
while(ikey) j--; //前移
if(idata;
if(b->lchild!=NULL||b->rchild!=NULL)
{
cout<<"("; //有左子树输出左括号
DispBTNode(b->lchild);
if(b->rchild!=NULL) //有右子树 输出右括号
cout<<",";
DispBTNode(b->rchild);
cout<<")";
}
}
}
int main()
{
int n,i,temp;
cout<<"************************"<>n;
BTNode *m;
BTNode w[2*N-1];
if(n0)
{
cout<<"请依次输入二叉树各节点的权值:";
for(i = 0; i < n; i++)
{
cin>>temp;
w[i].data = temp;
}
m=CreateHT(w,n);
cout<