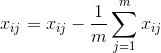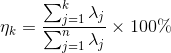PCA降维及python实现
定义
PCA(principal Component Analysis),主成分分析法。顾名思义,就是提取出数据中主要的成分,是一种数据压缩方法,常用于去除噪声、数据预处理,也是机器学习中常见的降维方法。
解释
专业一点讲,PCA就是用一个超平面(直线的高维推广)对所有样本进行恰当的表达。
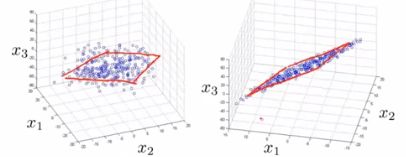
例如一个三维图形(特征数为3),我们想将它降低到二维(特征数为2),最容易想到的就是投影到一个平面上,但这个平面不一定恰好就是![]() 平面或者其他坐标轴平面,而是一个能尽量接近原始数据信息的平面(由于总是不可避免的会丢失一些信息,所以这也是PCA的缺点)。
平面或者其他坐标轴平面,而是一个能尽量接近原始数据信息的平面(由于总是不可避免的会丢失一些信息,所以这也是PCA的缺点)。
这个超平面应该具有以下性质:
- 最近重构性:样本点到这个超平面的距离都足够近;
- 最大可分性:样本点在这个超平面上的投影能尽量分开。
但根据这两种性质最终会得到等价的推导,见西瓜书P230.
此外,PCA与线性回归的区别:PCA是无监督学习,线性回归是监督学习。
步骤
对于样本集![]() ,有
,有![]() 个特征,即维数为
个特征,即维数为![]() ,每个特征有m个样本。我们想降低维数到
,每个特征有m个样本。我们想降低维数到![]() .
.
- 对所有样本进行中心化处理
![]() 表示
表示![]() 特征的第
特征的第![]() 个样本。
个样本。
即将每个元素减去它的平均值,这样可以增加基向量的正交性。
- 计算协方差矩阵及特征值、特征向量
协方差矩阵是一个![]() 的矩阵,且满足对称正定,矩阵内的每个元素
的矩阵,且满足对称正定,矩阵内的每个元素
其中![]() 是因为无偏估计。
是因为无偏估计。
协方差:
协方差衡量了两属性之间的关系,
当![]() 时,表示X与Y正相关;
时,表示X与Y正相关;
当![]() 时,代表X与Y负相关;
时,代表X与Y负相关;
当![]() 时,代表X与Y不相关。
时,代表X与Y不相关。
对于协方差矩阵![]() ,其特征值
,其特征值![]() (可能有多个)计算方法为
(可能有多个)计算方法为
![]()
再带入求得每个特征值对应的特征向量。
- 对特征值进行排序
选取最大的d个特征值对应的特征向量![]() .
.
投影为矩阵![]() ,完成数据压缩。
,完成数据压缩。
评价
通过特征值的计算我们可以得到 主成分所占的百分比,用来衡量模型的好坏。
对于前k个特征值所保留下的信息量计算方法如下:
此外,还可以通过交叉验证的方法进行评价。
实现
基于python带有功能强大的sklearn库,非常适合做机器学习,所以在此以python为例实现。
本人的python刚刚入门,很多函数不了解,所以参考了以下几篇文章:
https://blog.csdn.net/puredreammer/article/details/52255025
https://blog.csdn.net/u012102306/article/details/52294726
http://www.cnblogs.com/pinard/p/6243025.html
首先,训练集有6组数据,每组数据有4个特征,我们的目的是将其降到2维,也就是2个特征。
#coding=utf-8
import numpy as np
from sklearn.decomposition import PCA
X = np.array([[-1,2,66,-1], [-2,6,58,-1], [-3,8,45,-2], [1,9,36,1], [2,10,62,1], [3,5,83,2]]) #导入数据,维度为4
pca = PCA(n_components=2) #降到2维
pca.fit(X) #训练
newX=pca.fit_transform(X) #降维后的数据
# PCA(copy=True, n_components=2, whiten=False)
print(pca.explained_variance_ratio_) #输出贡献率
print(newX) #输出降维后的数据参数解释:
- n_components: 我们可以利用此参数设置想要的特征维度数目,可以是int型的数字,也可以是阈值百分比,如95%,让PCA类根据样本特征方差来降到合适的维数,也可以指定为string类型,MLE。
- copy: bool类型,TRUE或者FALSE,是否将原始数据复制一份,这样运行后原始数据值不会改变,默认为TRUE。
- whiten:bool类型,是否进行白化(就是对降维后的数据进行归一化,使方差为1),默认为FALSE。如果需要后续处理可以改为TRUE。
- explained_variance_: 代表降为后各主成分的方差值,方差值越大,表明越重要。
- explained_variance_ratio_: 代表各主成分的贡献率。
- inverse_transform(): 将降维后的数据转换成原始数据,X=pca.inverse_transform(newX)。
结果分析:
[0.95713353 0.03398198]
[[ 7.96504337 4.12166867]
[ -0.43650137 2.07052079]
[-13.63653266 1.86686164]
[-22.28361821 -2.32219188]
[ 3.47849303 -3.95193502]
[ 24.91311585 -1.78492421]]第一行为各主成分的贡献率,可以看出第一个特征占了很大比重 ,后面几行是降维后的数据。