Learning Convolutional Neural Networks for Graphs(学习图卷积神经网络)
目录
摘要
简介
2.相关工作
背景
卷积神经网络
图
4.学习任意图形的CNNs
4.1节点序列的选择
4.2邻域的组装( Neighborhood Assembly)
4.3图规范化
4.4卷积架构
5.复杂性和实施
6.实验
6.1运行时分析
6.2特征可视化
6.3图表分类
7.结论和未来工作
名词解释
摘要
提出一个学习任意图卷积神经网络的框架
简介
目标是将卷积神经网络应用于大量基于图的学习问题
考虑一下两个问题:
1.给定一组图形,学习一个可用于在看不见的图形上进行分类和回归问题的函数。任何两个图的节点不一定是对应的。例如,该集合的每个图可以模拟化合物,并且输出可以是将看不见的化合物映射到它们对抗癌细胞的活性水平的函数。
2.给定一个大图,学习图形表示,可用于推断看不见的图形属性,如节点类型和缺失边。
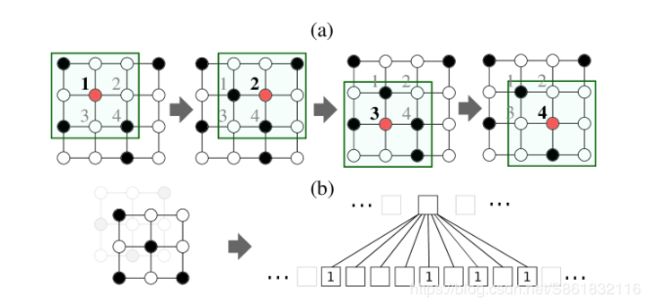
图1
如上图所示,图像表示为方形的网格图,节点代表像素。CNN遍历遍历节点序列,使图从a的4*4变成下面b的3*3的邻域图,(特征值的提取过程)(可以看到CNN遍历节点序列(图1(a)中的节点1-4)并为每个节点生成固定大小的邻域图(图1(b)中的3×3网格))。邻域图用作从像素节点读取特征值的接收字段。由于像素的隐式空间顺序,唯一地确定从左到右和从上到下创建邻域图的节点序列。
(然而,对于许多图形集合,缺少特定于问题的排序(空间,时间或其他),并且图形的节点不对应。)对于这句话我的理解是:很多图形不是像上面这个图一样节点的规则很整齐? 但是像素肯定是整齐的啊,所以我的理解是有冲突的.
面对这个情况,本论文认为必须解决如下两个问题:
(i)确定创建邻域图的节点序列
(ii)计算邻域图的归一化,即,从图表示到矢量空间表示的唯一映射。
提出的解决方法为:PATCHY-SAN
具体方式为:对于每个输入图,它首先确定创建邻域图的节点(及其顺序)。对于这些节点中的每一个,提取并精确化由k个节点组成的邻域,即,它被唯一地映射到具有固定线性顺序的空间。(先确定上图b的结构,然后再进行特征提取?)归一化邻域用作所考虑节点的接收域。最后,将卷积层和密集层等特征学习组件与归一化邻域图组合为CNN的接收域。
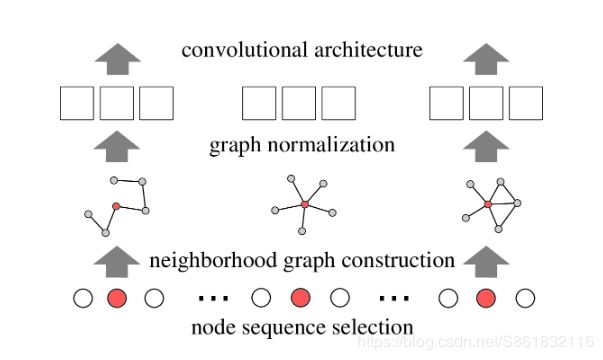
图2. PATCHY-SAN架构描述图
与现有方法比优点为:首先,它具有高效,(naively parallelizable)天真可并行化的特点,适用于大型图形。其次,从计算生物学到社交网络分析的许多应用,可视化学习到的网络图案非常重要。PATCHY-SAN支持功能可视化,提供对图形结构属性的深入了解。第三,PATCHY-SAN不是制作另一个图形内核,而是学习依赖于应用程序的功能,而无需进行特征工程。我们的理论贡献是关于图的归一化问题及其复杂性的定义;一种比较图表标记方法的方法;以及显示PATCHY-SAN在图像上推广CNN的结果。使用标准基准数据集,我们证明了与最先进的图形内核相比,学习的图形CNN既有效又有效。
2.相关工作
图形内核(Graph kernels)[“内核”就是用来圈定用来计算某一个像素的新值所用到的其周围像素点的一个框,内核除了一个框外,另外还有一个值是其锚点,用来代表的像素点在内核中的位置,通常就是在内核的中心。]允许基于内核的学习方法(如SVM)直接在图形上工作,图上的内核最初被定义为单个图的节点上的相似性函数,两个代表性的内核类是偏斜谱内核和基于小图的内核。基于小图的内核与本文有关,因为它基于固定大小的子图构建内核。这些子图通常称为图案或图形,反映了功能网络属性。由于子图枚举的组合复杂性,图基元内核仅限于节点较少的子图。一类有效的图形内核是Weisfeiler-Lehman(WL)内核,。但是,WL内核仅支持离散特征,并且在测试时使用训练样本数量的内存线性。PATCHY-SAN使用WL作为一种可能的标记程序来计算接收字段。深度图内核(Yanardag&Vishwanathan,2015)和图不变内核(Orsini等,2015)基于小子结构的存在【 the existence or count of small substructures】或计数(如最短路径)(Borgwardt&Kriegel,2005),graphlet,子树和其他图不变量(Haussler,1999; Orsini等,2015)。相比之下,PATCHY-SAN从图形数据中学习子结构,并不限于预定义的一组图案。此外,虽然所有图形核的训练复杂度至少是图形数量的二次方(Shervashidze等,2011),这对于大规模问题是禁止的,但PATCHY-SAN与图的数量呈线性关系。
图神经网络(GNN)(Scarselli等,2009)是一种在图上定义的递归神经网络架构。GNN应用递归神经网络在图结构上行走,传播节点表示直到达到固定点。然后将得到的节点表示用作分类和回归问题中的特征。GNN仅支持离散【大致意思就是变量值取整】标签并执行与每次学习迭代中图中的边和节点一样多的反向传播操作。门控图序列神经网络修改GNN以使用门控递归单位和输出序列。
最近的工作将CNN扩展到与低维网格结构不同的拓扑结构。然而,所有这些方法都假设一个全局图结构,即跨输入示例的顶点的对应关系。在图上执行卷积型操作,开发了一个特定图形特征的可微变量。
背景
卷积神经网络
典型的CNN由卷积层和密集层组成。第一卷积层的目的是提取在输入图像的局部区域内发现的常见图案。CNN将输入图像上的学习过滤器进行卷积,在图像中的每个图像位置计算内积,并将结果输出为张量,其深度为滤波器的数量。
图
G=(V,E)。 V:顶点集合, E:边集合,n为顶点数,m为边数。图形用n*n的矩阵表示,根据![]() 等于0或者1,表示i节点和j节点之间是否有边相连。d(u,v)表示u节点和v节点之间的最短路径长度。
等于0或者1,表示i节点和j节点之间是否有边相连。d(u,v)表示u节点和v节点之间的最短路径长度。![]() 表示V节点的全部邻域(距离为1的节点)
表示V节点的全部邻域(距离为1的节点)
没读明白的一段
图形标记程序的示例是节点程度和在网络分析中常用的其他中心性度量。例如,顶点v的中心度计算通过v的最短路径的分数。【Examples of graph labeling procedures are node degree and other measures of centrality commonly used in the analysis of networks.】Weisfeiler-Lehman算法(Weisfeiler&Lehman,1968; Douglas,2011)是用于划分图的顶点的过程。它也被称为颜色改进和朴素顶点【 naive vertex】分类。PATCHY-SAN应用这些标记程序(程度,页面等级,特征向量中心性等),在图的节点上施加顺序,替换缺失的依赖于应用程序的顺序(时间,空间等)。
同构与规范化【Isomorphism and Canonicalization.】.在几个应用领域中确定两个图是否是同构曲面的计算问题。图同构(GI)问题属于NP问题,但不属于P或NP-hard问题。(什么是P问题和NP问题?)在一些温和的限制条件下,已知GI在P中【GI is known to be in P】。例如,GI在P中表示有界度图(Luks, 1982)。图G的正则化是一个具有固定顶点阶的图,它与G同构,并且表示它的整个同构类。在实践中,图形规范化工具NAUTY表现出了显著的性能(McKay & Piperno, 2014)。
4.学习任意图形的CNNs
当CNN应用于图像时,接收场(正方形网格)以特定步长在每个图像上移动。接收字段为每个通道读取像素的特征值一次,并为每个通道创建一个值片(就是图1的过程)。由于图像的像素具有隐式排列 - 空间顺序 - 接收字段总是从左到右,从上到下移动。此外,空间顺序唯一地确定每个接收场的节点以及这些节点映射到向量空间表示的方式(参见图1(b))。因此,当且仅当像素的结构角色(它们在接收场内的空间位置)相同时,使用接收场的两个不同位置从两个像素读取的值被分配给相同的相对位置。(两个矩阵小块完全一样,提取出的特征值就是一样的)
为了显示CNN和PATCHY-SAN之间的连接,我们在图像上构建CNN,以识别表示图像的方形网格图中的节点序列,并为识别序列中的每个节点构建归一化邻域图 - 接收字段。对于缺少依赖于应用程序的节点顺序以及任何两个图形的节点尚未对齐的图形集合,我们需要为每个图形确定两点要素:(i)我们为其创建邻域的节点序列;(ii)a从图表示到矢量表示的唯一映射,使得在邻域图中具有相似结构角色的节点在矢量表示中类似地定位。
我们通过利用图形标记程序来解决这些问题,如果它们在图形中的结构角色相似,则将两个不同图形的节点分配到它们各自的邻接矩阵中的相似相对位置。给定一组图形,PATCHY-SAN(SELECTASSEMBLE-NORMALIZE)将以下步骤应用于每个图形:
(1)从图形中选择固定长度的节点序列;
(2)为所选序列中的每个节点组装一个固定大小的邻域;
(3)对提取的邻域图进行归一化;
(4)从得到的补丁序列中学习卷积神经网络的邻域表示。
对于以上四点的解决方式如下:
4.1节点序列的选择
节点序列选择是为每个输入图标识别为其创建接收字段的节点序列的过程。算法1列出了一个这样的过程。首先,输入图的顶点相对于给定的图标签进行排序。其次,使用给定步幅s遍历得到的节点序列,并且对于每个被访问节点,执行算法3以构造接收字段,直到已经创建了接收字段。步幅s确定相对于所选节点序列的两个连续节点之间的距离,为其创建接收场。如果节点数小于w,则算法为填充目的创建全零接收字段。
用于顶点序列选择的几种替代方法是可能的。例如,由图标标记的值引导的输入图的深度第一次遍历。我们将这些想法留给未来的工作。(节点序列选择的方法不止一种)
4.2邻域的组装( Neighborhood Assembly)
对于在前一步骤中识别的每个节点,必须构造一个接收场。算法3首先调用算法2来组装输入节点的局部邻域。邻域的节点是接收场的候选者。算法2(广度优先)列出了邻域组装步骤。给定节点v和接收字段k的大小作为输入,该过程执行广度第一搜索,探索距离v越来越远的顶点,并将这些顶点添加到集合N.如果收集的节点的数量小于k,则收集最近添加到N的顶点的1邻域,依此类推,直到至少k个顶点在N中,或者直到不再有要添加的邻居为止。注意,此时,N的大小可能与k不同。
4.3图规范化
通过对在前一步骤中组装的邻域进行归一化来构造节点的接收字段。如图3所示,归一化对邻域图的节点施加顺序,以便从无序图空间映射到具有线性顺序的向量空间。基本思想是利用图形标记程序,当且仅当它们在图形中的结构角色相似时,将两个不同图形的节点分配给相应邻接矩阵中的相似相对位置。
为了形式化这种直觉,我们定义了最优图规范化问题,该问题旨在找到相对于给定图形集合最佳的标记。
问题1(最佳图规范化):设G是一个带有k个节点的未标记图的集合。![]() 单射图的标记过程,
单射图的标记过程,![]() 为具有K个节点的图的距离度量,
为具有K个节点的图的距离度量,![]() 为K*K矩阵的距离测量
为K*K矩阵的距离测量
这个问题相当于找到一个图形标记程序![]() 。这样,对于从G中随机均匀绘制的任何两个图形,矢量空间中图形的距离(相对于基于l的邻接矩阵)的预期差异和图形空间中图形的距离最小化。最优图规范化问题是经典图规范化问题的推广。然而,规范标记算法仅对于同构图是最佳的,并且对于相似但不同构的图可能表现不佳。相反,对最优归一化问题的期望越小,标记就越好地对齐具有相似结构角色的节点。注意:相似性由
。这样,对于从G中随机均匀绘制的任何两个图形,矢量空间中图形的距离(相对于基于l的邻接矩阵)的预期差异和图形空间中图形的距离最小化。最优图规范化问题是经典图规范化问题的推广。然而,规范标记算法仅对于同构图是最佳的,并且对于相似但不同构的图可能表现不佳。相反,对最优归一化问题的期望越小,标记就越好地对齐具有相似结构角色的节点。注意:相似性由![]() 决定。
决定。
图3
图3.对在根节点v的邻域上产生的每个图进行归一化(红黑节点;节点的颜色代表距离根节点的距离)图形标记用于对节点进行排序并创建规范化的接收字段,其中一个是节点属性的大小为k(此处为:k=9),另一个为边属性的大小为k*k。规范化还包括裁剪多余节点和使用虚拟节点填充。每个顶点(边)属性对应于具有相应接收场的输入通道。
关于最优归一化问题,我们得到如下结果:
定理1:最优归一化问题是NP-hard问题
证明:通过减少子图同构。
PATCHY-SAN无法解决上述优化问题。相反,它可以比较不同的图形标记方法,并选择相对于给定图形集合表现最佳的方法。
定理2:设G是图的集合,设(G1;G‘’ 1);:::;(GN;G‘’ N)是一组图形对的序列从G中独立、均匀、随机地采样。
定理2使我们能够通过比较相应的估计器以无监督的方式比较不同的标记程序。在![]() 的假设下,估计值
的假设下,估计值![]() L越小,绝对差值越小。因此,我们可以简单的选择
L越小,绝对差值越小。因此,我们可以简单的选择![]() L最小的标签。例如,对于图的编辑距离和邻接矩阵的Ham ming距离,该
L最小的标签。例如,对于图的编辑距离和邻接矩阵的Ham ming距离,该![]() 假设成立。最后,请注意,所有上述结果都可以扩展到有向图。
假设成立。最后,请注意,所有上述结果都可以扩展到有向图。
图规范化问题和适当的图标记程序在局部图结构标准化中的应用是所提出方法的核心。在PATCHY-SAN框架内,我们规范化顶点v的邻域图。因此,对于任何两个顶点u,w,顶点的标记受到到v的图形距离的约束,如果u比w更接近v,则v总是排在高于w的位置。该定义确保v始终等级为1,并且顶点在G中越接近v,其在向量空间表示中的排序越高。(The labeling of the vertices is therefore constrained by the graph distance to v: for any two vertices u,w , if u is closer to v than w, then v is always ranked higher than w. This definition ensures that v has always rank 1, and that the closer a vertex is to v in G, the higher it is ranked in the vector space representation.)
由于大多数标记方法不是单射的,因此有必要打破相同标记节点之间的联系。为此,我们使用NAUTY(McKay&Piperno,2014)。 NAUTY接受先前节点分区作为输入,并通过选择按字典顺序排列的最大邻接矩阵来中断剩余的连接。众所周知,对于有界度的图,图同构在PTIME中(Luks,1982)。由于邻域图的常数k,该算法以原始图的大小在时间多项式中运行,并且平均在k中以时间线性运行(Babai等,1980)。(Due to the constant size k of the neighborhood graphs, the algorithm runs in time polynomial in the size of the original graph and, on average, in time linear in k (Babai et al., 1980).)我们的实验验证了计算图形neigborhoods的规范标记增加了可忽略不计的开销。
算法4列出了规范化过程。如果输入集U的大小大于k,则它首先应用基于ℓ的排序来选择前k个节点并重新计算较小节点集上的排名。如果U的大小小于k,则会添加断开的虚节点。最后,它引入顶点N上的子图,并将等级r作为先前着色进行规范化。
我们可以将PATCHY-SAN与CNN相关联,如下所示。
定理3:给定从图像中获取的像素序列。应用具有接收场尺寸![]() (2m-1)的平方
(2m-1)的平方![]() 的PATCHY-SAN,步幅s,无零填充,并且序列的1-WL归一化与接收场的第一层相同(接收场的固定排列)与接收场尺寸(2m-1)相同,跨步s,没有零填充。
的PATCHY-SAN,步幅s,无零填充,并且序列的1-WL归一化与接收场的第一层相同(接收场的固定排列)与接收场尺寸(2m-1)相同,跨步s,没有零填充。
证明:可以证明,如果输入图是方形网格,则为顶点构造的1-WL标准化接收字段始终是具有唯一顶点顺序的方形网格图。
4.4卷积架构
PATCHY-SAN能够处理顶点和边属性(离散和连续)。aV(v是下标)是顶点属性的数量,ae(e是下标)是边属性的数量。对于每个输入图G,它对顶点和边应用标准化的接收场,这导致一个(w,k,av(v是下标))和一个(w,k,k,ae(e是下标))张量。这些可以重新整形为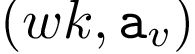 和
和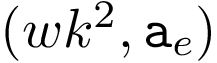 张量。请注意,
张量。请注意, 和
和 是输入通道的数量。我们现在可以将具有步幅和接收场尺寸k的1维卷积层应用于第一张,将
是输入通道的数量。我们现在可以将具有步幅和接收场尺寸k的1维卷积层应用于第一张,将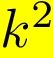 应用于第二张量。架构的其余部分可以任意选择。我们可以使用合并层来分别组合表示节点和边缘的卷积层。
应用于第二张量。架构的其余部分可以任意选择。我们可以使用合并层来分别组合表示节点和边缘的卷积层。
5.复杂性和实施
PATCHY-SAN用于创建接收字段的算法非常高效且可天然并行化,因为字段是独立生成的。我们可以显示以下渐近最坏情况的结果。定理4.设N是图的数量,令k为接收场大小,宽度为w,![]() 为具有n个顶点和m个边的图计算给定标记l的复杂度。PATCHY-SAN具有最坏情况的
为具有n个顶点和m个边的图计算给定标记l的复杂度。PATCHY-SAN具有最坏情况的![]() 复杂度,用于计算N个图的接收字段。
复杂度,用于计算N个图的接收字段。
证明:节点序列选择需要每个输入图的标记并检索k个排名最高的节点。对于标准化图补丁的创建,大多数计算工作花费在将标记过程l应用于其大小可能大于k的邻域上。设d是输入图G的最大度数,U是算法2返回的邻域。我们有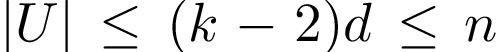 。术语
。术语![]() 来自k节点图上的图形规范化算法NAUTY的最坏情况复杂性(Miyazaki,1997)。
来自k节点图上的图形规范化算法NAUTY的最坏情况复杂性(Miyazaki,1997)。
例如,对于具有![]() (Berkholz等,2013)复杂度的Weisfeiler-Lehman算法,以及常数
(Berkholz等,2013)复杂度的Weisfeiler-Lehman算法,以及常数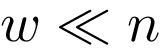 和
和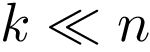 ,PATCHY-SAN的复杂度在N中是线性的,在m和n中是准线性的。
,PATCHY-SAN的复杂度在N中是线性的,在m和n中是准线性的。
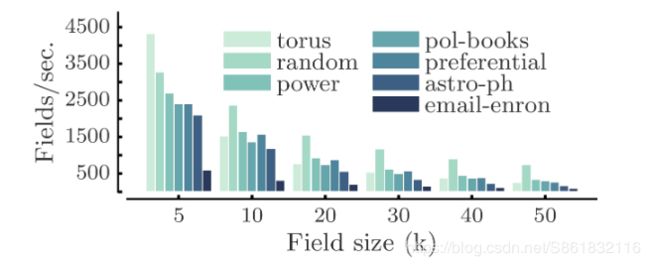
图4.不同图表上的每秒接收率字段
6.实验
我们进行了三种类型的实验:运行时分析,对学习特征的定性分析,以及与基准数据集上的图形内核的比较。
6.1运行时分析
我们通过将PATCHY-SAN应用于真实世界的图表来评估它的效率。目标是比较接收场产生的速率与现有技术CNN进行学习的速率。所有输入图都是Python模块GRAPHTOOL1集合的一部分。对于给定的图,我们使用PATCHY-SAN计算所有节点的接收字段,使用1维Weisfeiler-Lehman(Douglas,2011)(1-WL)算法进行归一化。圆环是一个具有10,000个节点的周期格子; random是一个随机无向图,有10,000个节点,度分布为 和
和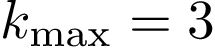 ;电力是代表美国电网拓扑结构的网络; polbooks是2004年总统大选期间出版的关于美国政治的共同购买网络;优先是优先附着网络模型,其中新添加的顶点具有3度; astro-ph是发布在天体物理学arxiv上的预印本作者之间的合作网络(Newman,2001); email-enron是一个由大约50万封电子邮件发送而来的通信网络(Leskovec et al。,2009)。所有实验都在具有64G RAM和单个2.8 GHz CPU的商用硬件上运行。
;电力是代表美国电网拓扑结构的网络; polbooks是2004年总统大选期间出版的关于美国政治的共同购买网络;优先是优先附着网络模型,其中新添加的顶点具有3度; astro-ph是发布在天体物理学arxiv上的预印本作者之间的合作网络(Newman,2001); email-enron是一个由大约50万封电子邮件发送而来的通信网络(Leskovec et al。,2009)。所有实验都在具有64G RAM和单个2.8 GHz CPU的商用硬件上运行。
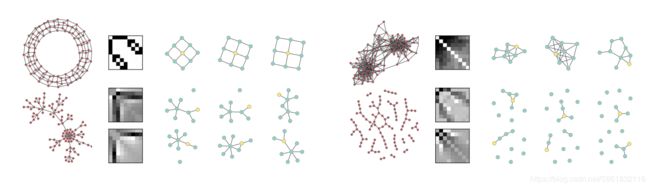
图5
图5.使用1维WL归一化接收场(用于圆环(周期点阵,左上)),优先附着图(Barab'asi&Albert 1999,左下),共同购买的RBM特征的可视化政治书籍网络(右上)和随机图表(右下角)。左侧描绘了具有大约100个节点的这些图的实例。通过将对应于该特征的除了隐藏节点之外的所有节点设置为零,可以直观地表示特征的权重(像素越暗,对应的权重越强)和从RBM采样的3个图形。黄色节点在邻接矩阵中具有位置1。 (最好看的颜色。)
图4描绘了每个输入图的每秒接收率。对于接收字段大小![]() 和
和![]() ,PATCHY-SAN创建的字段的速率大于
,PATCHY-SAN创建的字段的速率大于![]() ,但电子邮件安全的速率分别为
,但电子邮件安全的速率分别为![]() 和
和![]() 。对于
。对于![]() ,最大的测试尺寸字段的创建速率至少为
,最大的测试尺寸字段的创建速率至少为![]() 。具有2个卷积和2个密集层的CNN在同一台机器上以每秒约200-400个训练样本的速率学习。因此,产生接收场的速度足以使下游CNN饱和。
。具有2个卷积和2个密集层的CNN在同一台机器上以每秒约200-400个训练样本的速率学习。因此,产生接收场的速度足以使下游CNN饱和。
6.2特征可视化
可视化实验的目的是定性地研究诸如受限制的Boltzman机器(RBM)(Freund和Haussler,1992)之类的流行模型是否可以与PATCHY-SAN结合用于无监督的特征学习。对于每个输入图,我们为所有节点生成了接收字段,并将它们用作RBM的输入。RBM有100个隐藏节点,经过30个时期的训练,具有对比差异,学习率为0.01。我们将单层RBM学习的特征可视化为尺寸为9的1维Weisfeiler-Lehman(1-WL)归一化接收域。请注意,RBM学习的特征对应于重复出现的接收场模式。图5描绘了四个不同图形的一些特征和样本。
6.3图表分类
图表分类是将图表分配给几个类别之一的问题。 数据集。我们使用6个标准基准数据集来比较运行时和分类精度与最先进的图形内核:MUTAG,PCT,NCI1,NCI109,PRO TEIN和D&D。MUTAG(Debnath等,1991)是188种硝基化合物的数据集,其中类别表明该化合物是否对细菌具有诱变作用。PTC由344种化合物组成,其中的类别表明雄性和雌性大鼠的致癌性(Toivonen等,2003)。NCI1和NCI109是筛选针对非小细胞肺癌和卵巢癌细胞系的活性的化学化合物(Wale&Karypis,2006)。蛋白质是图形集合,其中节点是二级结构元素,边缘表示氨基酸序列或3D空间中的邻域。图表被分类为酶或非酶。 D&D是1178种蛋白质结构的数据集(Dobson&Doig,2003),分类为酶和非酶。
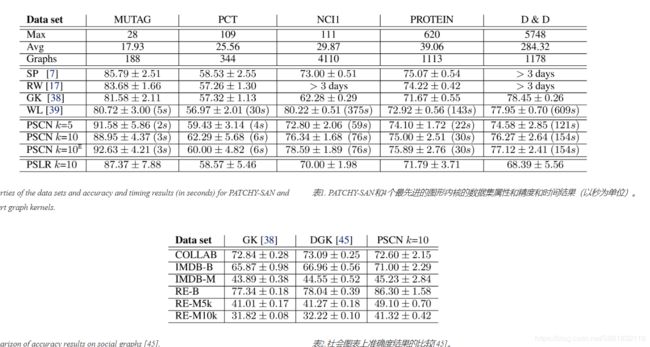
实验装置。我们将PATCHY-SAN与最短路径内核(SP)(Borgwardt&Kriegel,2005),随机游走内核(RW)(Gaertner等,2003),图形计数内核(GK)(Shervashidze等。 ,2009)和Weisfeiler-Lehman子树内核(WL)(Shervashidze等,2011)进行比较。与之前的工作类似(Yanardag&Vishwanathan,2015),我们将WL的height参数设置为2,将GK的graphlet大小设置为7,并从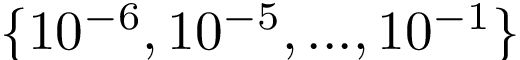 中选择RW的衰减因子。我们用LIB-SVM进行了10次交叉验证(Chang&Lin,2011),使用9倍进行训练,1次进行测试,并重复实验10次。我们报告平均预测准确度和标准偏差。
中选择RW的衰减因子。我们用LIB-SVM进行了10次交叉验证(Chang&Lin,2011),使用9倍进行训练,1次进行测试,并重复实验10次。我们报告平均预测准确度和标准偏差。
对于PATCHY-SAN(称为PSCN),我们使用1维WL标准化,宽度w等于平均节点数(见表1),以及![]() 和
和![]() 的接收字段大小。对于实验,我们仅使用节点属性。此外,我们为
的接收字段大小。对于实验,我们仅使用节点属性。此外,我们为![]() 进行了实验,我们使用合并层(
进行了实验,我们使用合并层( )组合节点和边缘的接收字段。为了进行公平的比较,我们使用了单个网络架构,其中包含两个卷积层,一个密集隐藏层和一个用于所有实验的softmax层。第一个卷积层有16个输出通道(特征图)。第二个转换层有8个输出通道,一个
)组合节点和边缘的接收字段。为了进行公平的比较,我们使用了单个网络架构,其中包含两个卷积层,一个密集隐藏层和一个用于所有实验的softmax层。第一个卷积层有16个输出通道(特征图)。第二个转换层有8个输出通道,一个![]() 的步幅,以及一个10的字段大小。卷积层具有整数线性单位。致密层有128个整流线性单元,辍学率为0.5。需要丢失和相对较少数量的神经元以避免对较小数据集的过度配置。我们优化的唯一超参数是迷你批量梯度体面算法RMSPROP的时期数和批量大小。以上所有都是用THEANO(Bergstra等,2010)包装纸KERAS(Chollet,2015)实施的。我们还在
的步幅,以及一个10的字段大小。卷积层具有整数线性单位。致密层有128个整流线性单元,辍学率为0.5。需要丢失和相对较少数量的神经元以避免对较小数据集的过度配置。我们优化的唯一超参数是迷你批量梯度体面算法RMSPROP的时期数和批量大小。以上所有都是用THEANO(Bergstra等,2010)包装纸KERAS(Chollet,2015)实施的。我们还在![]() 的补丁上应用了逻辑回归(PSLR)分类器。
的补丁上应用了逻辑回归(PSLR)分类器。
此外,我们在较大的社交图数据集(每个最多12000个图,平均400个节点)上使用相同的设置2进行实验,并将PATCHY-SAN与之前报告的图表计数结果(GK)和深度图形计数核(DGK)(Yanardag&Vishwanathan,2015)。我们使用规范化节点度作为PATCHY-SAN的属性,突出了它的一个优点:它可以轻松地包含连续特征。
结论:表1列出了实验结果。我们省略了NCI109的结果,因为它们几乎与NCI1相同。尽管使用了一体化的CNN架构,但CNN的准确性与现有的图形内核竞争非常激烈。在大多数情况下,接收场大小为10会产生最佳的分类精度。相对较高的方差可以用基准数据集的小尺寸和CNN超参数(除了纪元和批量大小)未调整到单个数据集的事实来解释。与图像和文本数据的体验类似,我们希望PATCHY-SAN对大型数据集的性能更佳。此外,PATCHY-SAN的效率比最有效的图形内核(WL)高2到8倍。我们预计对于具有大量图形的数据集,性能优势会更加明显。除了运行时间增加约10%之外,中性正常化的结果是相似的。应用于PATCHY-SAN接收字段的逻辑回归表现更差,这表明PATCHY-SAN与CNN一起工作特别好,CNN学习非线性特征组合并且在接收域之间共享权重。
PATCHY-SAN在社交图数据上也具有很强的竞争力。它在六个数据集中的四个数据集上显着优于其他两个内核,并在其余数据集上实现了联系。表2列出了实验结果。
7.结论和未来工作
我们提出了一个学习图形表示的框架,它与CNN一起特别有益。它结合了两个互补的过程:(a)选择覆盖图的大部分的节点序列,以及(b)为序列中的每个节点生成局部归一化邻域表示。实验表明,该方法与最先进的图形内核竞争。
未来工作的方向包括使用其他神经网络架构,如RNN;结合不同的接收场尺寸;使用RBM和自动编码器进行预训练;和基于方法思想的统计关系模型。
名词解释
归一化:数据标准化(Normalization),也称为归一化,归一化就是将你需要处理的数据在通过某种算法经过处理后,限制将其限定在你需要的一定的范围内。(以某个值或者界限作为新的对比点)
图形标记程序:
同构图:graph isomorphism