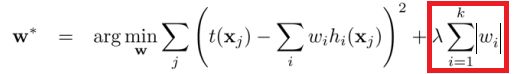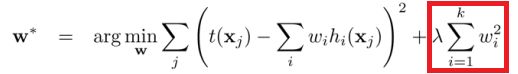常见机器学习面试问题

机器学习问题

学习曲线 判断是过拟合还是欠拟合

当模型出现欠拟合和过拟合情况时，学习曲线一般有不同形状，如下图所示。其中虚线表示在训练集上的结果，实线表示在验证集上的结果。

欠拟合情况：随着训练样本数增大，训练集得分和验证集得分收敛，并且两者的收敛值很接近。

过拟合情况：随着训练样本数增大，训练集得分和验证集得分相差还是很大。

学习曲线就是通过画出不同训练集大小时训练集和交叉验证的准确率，可以看到模型在新数据上的表现，进而来

判断模型是否方差偏高或偏差过高，以及增大训练集是否可以减小过拟合。

为什么用交叉熵代替二次代价函数？

二次代价函数
$$J=\frac{1}{2n}\sum _x\Vert y(x)-a(x){\Vert }^2$$
其对w和b的偏导数为
$$\frac{\partial J}{\partial w}=(a-y){\sigma }^{\prime }(z)x$$

$$\frac{\partial J}{\partial b}=(a-y){\sigma }^{\prime }(z)$$

偏导数受到激活函数的导数影响，sigmoid函数在它在定义域内的梯度都不大于0.25。这样训练会非常的慢。

sigmoid函数的导数为
$$g^{\prime }(x)=g(x)\ast (1-g(x))=\frac{e^x}{e^{2x}+2e^x+1}=\frac{1}{e^x+\frac{1}{e^x}+2}\le \frac{1}{2+2}=\frac{1}{4}$$
其值域是$(0,\frac{1}{4}]$

而使用交叉熵
$$J=-\frac{1}{n}\sum _{x}ylna+(1-y)ln(1-a)$$
其对w和b的偏导数为
$$\frac{\partial J}{\partial w_j}=\frac{1}{n}\sum _x{x}_j(\sigma (z)-y)$$

$$\frac{\partial J}{\partial b}=\frac{1}{n}\sum _x(\sigma (z)-y)$$

权重学习的速度受到sigmoid(z)-y影响，更大的误差，就有更快的学习速度，避免了二次代价函数的学习缓慢的情况。

MAE损失函数和MSE损失函数

平均绝对值误差（也称L1损失）
$$MAE=\sum _{i=1}^n|y_i-y_i^p|$$
平均绝对误差（MAE）是另一种用于回归模型的损失函数。MAE是目标值和预测值之差的绝对值之和。其只衡量了预测值误差的平均模长，而不考虑方向，取值范围也是从0到正无穷（如果考虑方向，则是残差/误差的总和——平均偏差（MBE））。

简单来说，MSE计算简便，但MAE对异常点有更好的鲁棒性。

第一个例子中，预测值和真实值很接近，而且误差的方差也较小。第二个例子中，因为存在一个异常点，而导致误差非常大。

如果训练数据被异常点所污染，那么MAE损失就更好用（比如，在训练数据中存在大量错误的反例和正例标记，但是在测试集中没有这个问题）。

众所周知，对异常值而言，中位数比均值更加鲁棒，因此MAE对于异常值也比MSE更稳定。

然而MAE存在一个严重的问题（特别是对于神经网络）：更新的梯度始终相同，也就是说，即使对于很小的损失值，梯度也很大。这样不利于模型的学习。为了解决这个缺陷，我们可以使用变化的学习率，在损失接近最小值时降低学习率。

总而言之，处理异常点时，L1损失函数更稳定，但它的导数不连续，因此求解效率较低。L2损失函数对异常点更敏感，但通过令其导数为0，可以得到更稳定的封闭解。

二者兼有的问题是：在某些情况下，上述两种损失函数都不能满足需求。例如，若数据中90%的样本对应的目标值为150，剩下10%在0到30之间。那么使用MAE作为损失函数的模型可能会忽视10%的异常点，而对所有样本的预测值都为150。

这是因为模型会按中位数来预测。而使用MSE的模型则会给出很多介于0到30的预测值，因为模型会向异常点偏移。上述两种结果在许多商业场景中都是不可取的。

这些情况下应该怎么办呢？最简单的办法是对目标变量进行变换。而另一种办法则是换一个损失函数，这就引出了下面要讲的第三种损失函数，即Huber损失函数。

Huber损失，平滑的平均绝对误差

Huber损失对数据中的异常点没有平方误差损失那么敏感。它在0也可微分。本质上，Huber损失是绝对误差，只是在误差很小时，就变为平方误差。误差降到多小时变为二次误差由超参数$\delta$来控制。当Huber损失在$[0-\delta ,0+\delta ]$之间时，等价为MSE，而在$[-\infty ,\delta ]$和$[\delta ,+\infty ]$时为MAE。

Huber损失（Y轴）与预测值（X轴）图示。真值取0

这里超参数delta的选择非常重要，因为这决定了你对与异常点的定义。当残差大于$\delta$，应当采用L1（对较大的异常值不那么敏感）来最小化，而残差小于超参数，则用L2来最小化。

为何要使用Huber损失？

使用MAE训练神经网络最大的一个问题就是不变的大梯度，这可能导致在使用梯度下降快要结束时，错过了最小点。而对于MSE，梯度会随着损失的减小而减小，使结果更加精确。

在这种情况下，Huber损失就非常有用。它会由于梯度的减小而落在最小值附近。比起MSE，它对异常点更加鲁棒。因此，Huber损失结合了MSE和MAE的优点。但是，Huber损失的问题是我们可能需要不断调整超参数$\delta$。

理解L1和L2损失函数和正则化

在机器学习实践中，你也许需要在神秘的L1和L2中做出选择。通常的两个决策为：1) L1范数 vs L2范数 的损失函数； 2) L1正则化 vs L2正则化。

作为损失函数

L1范数损失函数，也被称为最小绝对值偏差（LAD），最小绝对值误差（LAE）。总的说来，它是把目标值（$Y_i$）与估计值($f(x_i)$)的绝对差值的总和（$S$）最小化：
$$S=\sum _{i=1}^n|Y_i-f(x_i)|.$$

L2范数损失函数，也被称为最小平方误差（LSE）。总的来说，它是把目标值$(Y_i)$与估计值（$f(x_i)$）的差值的平方和（$S$）最小化：
$$S=\sum _{i=1}^n(Y_i-f(x_i){)}^2.$$

L1范数与L2范数作为损失函数的区别能快速地总结如下：

L2损失函数	L1损失函数
不是非常的鲁棒（robust）	鲁棒
稳定解	不稳定解
总是一个解	可能多个解

鲁棒性（robustness），根据维基百科，被解释为：

因为与最小平方相比，最小绝对值偏差方法的鲁棒性更好，因此，它在许多场合都有应用。最小绝对值偏差之所以是鲁棒的，是因为它能处理数据中的异常值。这或许在那些异常值可能被安全地和有效地忽略的研究中很有用。如果需要考虑任一或全部的异常值，那么最小绝对值偏差是更好的选择。

从直观上说，因为L2范数将误差平方化（如果误差大于1，则误差会放大很多），模型的误差会比L1范数来得大（ e vs e^2 ），因此模型会对这个样本更加敏感，这就需要调整模型来最小化误差。如果这个样本是一个异常值，模型就需要调整以适应单个的异常值，这会牺牲许多其它正常的样本，因为这些正常样本的误差比这单个的异常值的误差小。

稳定性，根据维基百科，被解释为：

最小绝对值偏差方法的不稳定性意味着，对于数据集的一个小的水平方向的波动，回归线也许会跳跃很大。在一些数据结构（data configurations）上，该方法有许多连续解；但是，对数据集的一个微小移动，就会跳过某个数据结构在一定区域内的许多连续解。（The method has continuous solutions for some data configurations; however, by moving a datum a small amount, one could “jump past” a configuration which has multiple solutions that span a region. ）在跳过这个区域内的解后，最小绝对值偏差线可能会比之前的线有更大的倾斜。相反地，最小平方法的解是稳定的，因为对于一个数据点的任何微小波动，回归线总是只会发生轻微移动；也就说，回归参数是数据集的连续函数。

下面的图是用真实数据和真实拟合模型生成的：

这里使用的基本模型为梯度提升回归（GradientBoostingRegressor），使用L1范数和L2范数作为损失函数。绿线和红色分别代表了模型使用L1范数与L2范数作为损失函数时的情形。实线代表了训练的模型中不含有异常值（橙色）的情形，虚线代表了训练的模型中含有异常值（橙色）的情形。
  我缓慢地将这个异常值从左向右移动，使得它在中间时不那么异常，而在左右两边时更加异常。当这个异常值不那么异常时（在中间的情形），在拟合直线的时候，L2范数的变动较小，而L1范数的表动较大。
  当这个异常值更加异常（上左位置，下右位置，它们离左、右两边更加远）时，这两个范数都有大的变动，但是再一次地，L1范数总体上比L2范数变动更大。
  通过数据可视化，我们能够对这两个损失函数的稳定性有更好的认知。

作为正规化

在机器学习中，正规化是防止过拟合的一种重要技巧。从数学上讲，它会增加一个正则项，防止系数拟合得过好以至于过拟合。L1与L2的区别只在于，L2是权重的平方和，而L1就是权重的和。如下：

最小平方损失函数的L1正则化：

最小平方损失函数的L2正则化：

它们的性质的区别能快速地总结如下：

L2正则化	L1正则化
计算效率高（因为有解析解）	在非稀疏情形下计算效率低
非稀疏输出	稀疏输出
无特征选择	内置特征选择

解的唯一性是一个更简单的性质，但需要一点想象。首先，看下图：

绿色的线（L2范数）是唯一的最短的路径，而红色、蓝色、黄色线条（L1范数）都是同一路径，长度一样（12）。可以将其扩展至n-维的情形。这就是为什么L2范数有唯一解而L1并不是。
  内置特征选择是L1范数被经常提及的有用的性质，而L2范数并不具备。这是L1范数的自然结果，它趋向于产生稀疏的系数（在后面会解释）。假设模型有100个系数，但是仅仅只有其中的10个是非零的，这实际上是说“其余的90个系数在预测目标值时都是无用的”。L2范数产生非稀疏的系数，因此它不具备这个性质。
  稀疏性指的是一个矩阵（或向量）中只有少数的项是非零的。L1范数具备性质：产生许多0或非常小的系数和少量大的系数。
  计算效率。L1范数没有一个解析解，但是L2范数有。这就允许L2范数在计算上能高效地计算。然而，L1范数的解具备稀疏性，这就允许它可以使用稀疏算法，以使得计算更加高效。

KNN里面，如果你要自定义metric(不用内置的欧氏距离，曼哈顿距离)，而kd-tree只能用内置的metric，你怎么做？

一般sklearn中的算法是支持自定义距离或者评价指标的。

>>> def mydist(x, y, **kwargs):
...     return np.sum((x-y)**kwargs["metric_params"]["power"])
...
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> Y = np.array([-1, -1, -2, 1, 1, 2])
>>> nbrs = KNeighborsClassifier(n_neighbors=4, algorithm='ball_tree',
...            metric=mydist, metric_params={"power": 2})
>>> nbrs.fit(X, Y)
KNeighborsClassifier(algorithm='ball_tree', leaf_size=30,                               
       metric=<function mydist at 0x7fd259c9cf50>, n_neighbors=4, p=2,
       weights='uniform')
>>> nbrs.kneighbors(X)
(array([[  0.,   1.,   5.,   8.],
       [  0.,   1.,   2.,  13.],
       [  0.,   2.,   5.,  25.],
       [  0.,   1.,   5.,   8.],
       [  0.,   1.,   2.,  13.],
       [  0.,   2.,   5.,  25.]]),
 array([[0, 1, 2, 3],
       [1, 0, 2, 3],
       [2, 1, 0, 3],
       [3, 4, 5, 0],
       [4, 3, 5, 0],
       [5, 4, 3, 0]]))

SVM里面，如果增加了惩罚系数，它的损失函数会怎么变？

C是惩罚系数，增大惩罚系数，对误分类的惩罚变大，损失函数变大。

SVM核函数选择

一般用线性核和高斯核，也就是Linear核与RBF核

需要注意的是需要对数据归一化处理，很多使用者忘了这个小细节

然后一般情况下RBF效果是不会差于Linear

但是时间上RBF会耗费更多，其他同学也解释过了

下面是吴恩达的见解：

1. 如果Feature的数量很大，跟样本数量差不多，这时候选用LR或者是Linear Kernel的SVM
2. 如果Feature的数量比较小，样本数量一般，不算大也不算小，选用SVM+Gaussian Kernel
3. 如果Feature的数量比较小，而样本数量很多，需要手工添加一些feature变成第一种情况

极大似然估计和最大后验估计

隐马尔科夫模型基本问题及其相应的算法：

1、评估问题：概率计算问题：给定模型和观测序列，计算在模型下观测序列出现的概率。

前向、后向算法解决的是一个评估问题，即给定一个模型，求某特定观测序列的概率，用于评估该序列最匹配的模型。

2、模型学习问题：已知观测序列，估计模型中的参数，使得在该模型下观测序列概率最大，即用极大似然估计的方法估计参数。

Baum-Welch算法解决的是一个模型训练问题，即参数估计，是一种无监督的训练方法，主要通过EM迭代实现；即只有观测序列，无状态序列时训练模型。

极大似然估计：观测序列和相应的状态序列都存在的监督学习算法，用来估计参数。

3、解码问题/预测问题：已知模型和观测序列，给定观测序列，求最可能的对应的状态序列。

维特比算法解决的是给定一个模型和某个特定的输出序列，求最可能产生这个输出的状态序列。如通过海藻变化（输出序列）来观测天气（状态序列），是预测问题，通信中的解码问题！

线性分类器最佳准则

• 感知器算法 感知准则函数
• 支持向量机
• 线性判别分析 Fisher准则

贝叶斯分类器不是线性分类器。
SVM可通过正则化系数控制模型的复杂度，避免过拟合。

解决类别不均衡问题

• 重采样
• 欠采样
• 调整权值

机器学习中做特征选择时，常用的方法

通常来说，从两个方面考虑来选择特征：

• 特征是否发散：如果一个特征不发散，例如方差接近于0，也就是说样本在这个特征上基本上没有差异，这个特征对于样本的区分并没有什么用。
• 特征与目标的相关性：这点比较显见，与目标相关性高的特征，应当优选选择。除方差法外，本文介绍的其他方法均从相关性考虑。

根据特征选择的形式又可以将特征选择方法分为3种：

• Filter：过滤法，按照发散性或者相关性对各个特征进行评分，设定阈值或者待选择阈值的个数，选择特征。

  • 方差选择法
    先要计算各个特征的方差，然后根据阈值，选择方差大于阈值的特征。

  • 相关系数法
    先要计算各个特征对目标值的相关系数以及相关系数的P值

  • 卡方检验
    卡方检验这个统计量的含义就是自变量与因变量的相关性

  • 互信息法
    递归消除特征法使用一个基模型来进行多轮训练，每轮训练后，消除若干权值系数的特征，再基于新的特征集进行下一轮训练

  • 也是评价定性自变量对定性因变量的相关性的

• Wrapper：包装法，根据目标函数（通常是预测效果评分），每次选择若干特征，或者排除若干特征。

  • 递归特征消除法
    递归消除特征法使用一个基模型来进行多轮训练，每轮训练后，消除若干权值系数的特征，再 基于新的特征集进行下一轮训练

• Embedded：嵌入法，先使用某些机器学习的算法和模型进行训练，得到各个特征的权值系数，根据系数从大到小选择特征。类似于Filter方法，但是是通过训练来确定特征的优劣。

  • 基于惩罚项的特征选择法
    比如L1正则化，可以帮助选择特征

  • 基于树模型的特征选择法
    树模型中GBDT也可用来作为基模型进行特征选择

机器学习中的生成模型和判别模型：

生成模型

• 朴素贝叶斯
• 高斯混合模型
• 隐马尔科夫模型
• 马尔科夫随机场
• LDA主题模型

判别模型

• 逻辑回归
• K近邻
• SVM
• 神经网络
• 条件随机场

PDF PMF CDF

PDF：概率密度函数（probability density function）, 在数学中，连续型随机变量的概率密度函数（在不至于混淆时可以简称为密度函数）是一个描述这个随机变量的输出值，在某个确定的取值点附近的可能性的函数。

PMF : 概率质量函数（probability mass function), 在概率论中，概率质量函数是离散随机变量在各特定取值上的概率。

CDF : 累积分布函数 (cumulative distribution function)，又叫分布函数，是概率密度函数的积分，能完整描述一个实随机变量X的概率分布。

缺失值的处理方法

由于调查、编码和录入误差，数据中可能存在一些无效值和缺失值，需要给予适当的处理。常用的处理方法有：估算，整例删除，变量删除和成对删除。

估算(estimation)。最简单的办法就是用某个变量的样本均值、中位数或众数代替无效值和缺失值。这种办法简单，但没有充分考虑数据中已有的信息，误差可能较大。另一种办法就是根据调查对象对其他问题的答案，通过变量之间的相关分析或逻辑推论进行估计。例如，某一产品的拥有情况可能与家庭收入有关，可以根据调查对象的家庭收入推算拥有这一产品的可能性。

整例删除(casewise deletion)是剔除含有缺失值的样本。由于很多问卷都可能存在缺失值，这种做法的结果可能导致有效样本量大大减少，无法充分利用已经收集到的数据。因此，只适合关键变量缺失，或者含有无效值或缺失值的样本比重很小的情况。

变量删除(variable deletion)。如果某一变量的无效值和缺失值很多，而且该变量对于所研究的问题不是特别重要，则可以考虑将该变量删除。这种做法减少了供分析用的变量数目，但没有改变样本量。

成对删除(pairwise deletion)是用一个特殊码(通常是9、99、999等)代表无效值和缺失值，同时保留数据集中的全部变量和样本。但是，在具体计算时只采用有完整答案的样本，因而不同的分析因涉及的变量不同，其有效样本量也会有所不同。这是一种保守的处理方法，最大限度地保留了数据集中的可用信息。

采用不同的处理方法可能对分析结果产生影响，尤其是当缺失值的出现并非随机且变量之间明显相关时。因此，在调查中应当尽量避免出现无效值和缺失值，保证数据的完整性。

基于核的机器学习方法

• SVM
• LDA线性判别分析
• 径向基函数（Radial Basis Function ，RBF)

HMM MEMM CRF

HMM:隐马尔可夫模型

MEMM: 最大熵隐马尔可夫模型

CRF：条件随机场

CRF 的优点：特征灵活，可以容纳较多的上下文信息，能够做到全局最优

CRF 的缺点：速度慢

CRF没有HMM那样严格的独立性假设条件，因而可以容纳任意的上下文信息。和HMM相比，特征设计灵活（与ME一样）

（2）同时，和MEMM相比，由于CRF计算全局最优输出节点的条件概率，它还克服了最大熵马尔可夫模型标记偏置（Label-bias）的缺点。

（3）和MEMM相比，CRF是在给定需要标记的观察序列的条件下，计算整个标记序列的联合概率分布，而不是在给定当前状态条件下，定义下一个状态的状态分布。

缺点：训练代价大、复杂度高

梯度提升决策树（GBDT）和随机森林（RF）的异同

GBDT（Gradient Boosting Decision Tree）

DT + Boosting = GBDT
GBDT是一种boosting算法。boosting工作机制：先从初始训练集训练处一个基学习器，然后在根据基学习器的表现对训练样本分布进行调整，使得先前的基学习器做错的训练样本在后续获得更多关注（增加错误样本权重），然后基于调整后的样本分布训练下一个基学习器，如此重复，直到基学习器达到指定的T时，最终将T个基学习器进行加权结合，得出预测。
RF（Random Forest）
DT + Bagging = RF
随机森林是bagging的一种扩展，在k个数据集选择的时候后，引入了随机属性选择。加入所有属性个数为d，k是随机选择的属性个数。那么k=d的时候，就没有改变。那么k=1的时候后，随机选择一个属性用于计算。推荐的k=log2d.
随机森林的基学习器一般是决策树算法-主要，也有神经网络。

随机森林是对bagging算法的一点改动，但是根能提现样本集之间的差异性。会提高最终预测结果的泛化能力。

GBDT和随机森林的相同点

1、都是由多棵树组成

2、最终的结果都是由多棵树一起决定

GBDT和随机森林的不同点

1、组成随机森林的树可以是分类树，也可以是回归树；而GBDT只由回归树组成

2、组成随机森林的树可以并行生成；而GBDT只能是串行生成

3、对于最终的输出结果而言，随机森林采用多数投票等；而GBDT则是将所有结果累加起来，或者加权累加起来

4、随机森林对异常值不敏感，GBDT对异常值非常敏感

5、随机森林对训练集一视同仁，GBDT是基于权值的弱分类器的集成

6、随机森林是通过减少模型方差提高性能，GBDT是通过减少模型偏差提高性能

stacking和blending

Stacking的主要思想是训练模型来学习使用底层学习器的预测结果，下图是一个5折stacking中基模型在所有数据集上生成预测结果的过程，次学习器会基于模型的预测结果进行再训练，单个基模型生成预测结果的过程是：

首先将所有数据集生成测试集和训练集（假如训练集为10000,测试集为2500行），那么上层会进行5折交叉检验，使用训练集中的8000条作为训练集，剩余2000行作为验证集（橙色）

每次验证相当于使用了蓝色的8000条数据训练出一个模型，使用模型对验证集进行验证得到2000条数据，并对测试集进行预测，得到2500条数据，这样经过5次交叉检验，可以得到中间的橙色的5*2000条验证集的结果(相当于每条数据的预测结果)，5*2500条测试集的预测结果。
接下来会将验证集的5*2000条预测结果拼接成10000行长的矩阵，标记为A1，而对于5*2500行的测试集的预测结果进行加权平均，得到一个2500一列的矩阵，标记为B1。
上面得到一个基模型在数据集上的预测结果A1、B1,这样当我们对3个基模型进行集成的话，相于得到了A1、A2、A3、B1、B2、B3六个矩阵。

之后我们会将A1、A2、A3并列在一起成10000行3列的矩阵作为training data,B1、B2、B3合并在一起成2500行3列的矩阵作为testing data，让下层学习器基于这样的数据进行再训练。

再训练是基于每个基础模型的预测结果作为特征（三个特征），次学习器会学习训练如果往这样的基学习的预测结果上赋予权重w，来使得最后的预测最为准确。

以上就是Stacking的思想，进行Stacking集成同样需要基学习器尽量保持独立，效果相近。

Stacking特点
使用stacking，组合1000多个模型，有时甚至要计算几十个小时。但是，这些怪物般的集成方法同样有着它的用处:
(1)它可以帮你打败当前学术界性能最好的算法
(2)我们有可能将集成的知识迁移到到简单的分类器上
(3)自动化的大型集成策略可以通过添加正则项有效的对抗过拟合，而且并不需要太多的调参和特征选择。所以从原则上讲，stacking非常适合于那些“懒人”
(4)这是目前提升机器学习效果最好的方法，或者说是最效率的方法human ensemble learning 。

Stacking和Blending对比

1.Blending方式和Stacking方式很类似，相比Stacking更简单点，两者区别是：

blending是直接准备好一部分10%留出集只在留出集上继续预测，用不相交的数据训练不同的 Base Model，将它们的输出取（加权）平均。实现简单，但对训练数据利用少了。

2.blending 的优点是：比stacking简单，不会造成数据穿越（所谓数据创越，就比如训练部分数据时候用了全局的统计特征，导致模型效果过分的好），generalizers和stackers使用不同的数据，可以随时添加其他模型到blender中。

3.缺点在于：blending只使用了一部分数据集作为留出集进行验证，而stacking使用多折交叉验证，比使用单一留出集更加稳健

4.两个方法都挺好，看偏好了，可以一部分做Blending、一部分做Stacking。

再来看一张非常美丽的图：

处理欠拟合和过拟合

(1)解决欠拟合的方法：

1、增加新特征，可以考虑加入进特征组合、高次特征，来增大假设空间;
2、尝试非线性模型，比如核SVM 、决策树、DNN等模型;
3、如果有正则项可以较小正则项参数 $\lambda$;
4、Boosting ,Boosting 往往会有较小的 Bias，比如 Gradient Boosting 等.

(2)解决过拟合的方法：

1、交叉检验，通过交叉检验得到较优的模型参数;
2、特征选择，减少特征数或使用较少的特征组合，对于按区间离散化的特征，增大划分的区间;
3、正则化，常用的有 L1、L2 正则。而且 L1正则还可以自动进行特征选择;
4、如果有正则项则可以考虑增大正则项参数 lambda;
5、增加训练数据可以有限的避免过拟合;
6、Bagging ,将多个弱学习器Bagging 一下效果会好很多，比如随机森林等.

（3）DNN中常见的方法：

1、早停策略。本质上是交叉验证策略，选择合适的训练次数，避免训练的网络过度拟合训练数据。
2、DropOut策略。所谓的Dropout指的是在用前向传播算法和反向传播算法训练DNN模型时，一批数据迭代时，随机的从全连接DNN网络中去掉一部分隐藏层的神经元。　在对训练集中的一批数据进行训练时，我们随机去掉一部分隐藏层的神经元，并用去掉隐藏层的神经元的网络来拟合我们的一批训练数据。当然天下没有免费的午餐，由于dropout会将原始数据分批迭代，因此原始数据集最好较大，否则模型可能会欠拟合。
3、Batch Normalization

线性分类器与非线性分类器的区别以及优劣

线性和非线性是针对，模型参数和输入特征来讲的；比如输入$x$，模型$y=ax+a{x}^2$那么就是非线性模型，如果输入是$x$和$X^2$则模型是线性的。
线性分类器可解释性好，计算复杂度较低，不足之处是模型的拟合效果相对弱些。
非线性分类器效果拟合能力较强，不足之处是数据量不足容易过拟合、计算复杂度高、可解释性不好。
常见的线性分类器有：LR,贝叶斯分类，单层感知机、线性回归
常见的非线性分类器：决策树、RF、GBDT、多层感知机
SVM两种都有（看线性核还是高斯核）

L1和L2正则先验分别服从什么分布

面试中遇到的，L1和L2正则先验分别服从什么分布，L1是拉普拉斯分布，L2是高斯分布。
先验就是优化的起跑线, 有先验的好处就是可以在较小的数据集中有良好的泛化性能，当然这是在先验分布是接近真实分布的情况下得到的了，从信息论的角度看，向系统加入了正确先验这个信息，肯定会提高系统的性能。
对参数引入高斯正态先验分布相当于L2正则化, 这个大家都熟悉：

对参数引入拉普拉斯先验等价于 L1正则化, 如下图：

从上面两图可以看出, L2先验趋向零周围, L1先验趋向零本身。

L1范数会产生稀疏的模型，有特征选择的效果，减少了特征的维数，因此可以防止过拟合。而L2范数会使模型的参数变小，更小的参数值意味着模型的复杂度更低，对训练数据的拟合刚好（奥卡姆剃刀）

随机森林如何评估特征重要性？

随机森林中进行特征重要性的评估思想为：
判断每个特征在随机森林中的每颗树上做了多大的贡献，然后取个平均值，最后比一比特征之间的贡献大小。其中关于贡献的计算方式可以是基尼指数或袋外数据错误率。

1.RF评估特征重要性–基于基尼指数

基尼指数计算方法：k 代表 k 个类别，[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-B1pLr07s-1573473063524)(https://math.jianshu.com/math?formula=p_k)]代表类别 k的样本权重。

那么特征在节点m上的重要性，即节点m分枝前后的Gini指数变化量为 ：(其中，GIl和GIr分别表示分枝后两个新节点的Gini指数)

2.RF评估特征重要性–基于袋外数据

对于一棵树，用OOB样本可以得到误差 e1，然后随机改变OOB中的第 j 列，保持其他列不变，对第 j 列进行随机的上下置换，得到误差 e2。至此，可以用 e1-e2 来刻画特征 j 的重要性。其依据就是，如果一个特征很重要，那么其变动后会非常影响测试误差，如果测试误差没有怎么改变，则说明特征j不重要。

而该方法中涉及到的对数据进行打乱的方法通常有两种：
1）是使用uniform或者gaussian抽取随机值替换原特征；
2）是通过permutation的方式将原来的所有N个样本的第 i 个特征值重新打乱分布（相当于重新洗牌）。

比较而言，第二种方法更加科学，保证了特征替代值与原特征的分布是近似的（只是重新洗牌而已）。这种方法叫做permutation test（随机排序测试），即在计算第 i 个特征的重要性的时候，将N个样本的第 i 个特征重新洗牌

bagging与boosting两种集成模型的偏差bias以及方差variance 的理解

XGBoost的优势

XGBoost算法可以给预测模型带来能力的提升。当我对它的表现有更多了解的时候，当我对它的高准确率背后的原理有更多了解的时候，我发现它具有很多优势：

1. 正则化

• 标准GBM的实现没有像XGBoost这样的正则化步骤。正则化对减少过拟合也是有帮助的。
• 实际上，XGBoost以"正则化提升(regularized boosting)"技术而闻名。

2. 并行处理

• XGBoost可以实现并行处理，相比GBM有了速度的飞跃。
• 不过，众所周知，Boosting算法是顺序处理的，它怎么可能并行呢？每一课树的构造都依赖于前一棵树，那具体是什么让我们能用多核处理器去构造一个树呢？我希望你理解了这句话的意思。如果你希望了解更多，点击这个链接。
• XGBoost 也支持Hadoop实现。
• boosting不是一种串行的结构吗?怎么并行的？注意xgboost的并行不是tree粒度的并行，xgboost也是一次迭代完才能进行下一次迭代的（第t次迭代的代价函数里包含了前面t-1次迭代的预测值）。xgboost的并行是在特征粒度上的。我们知道，决策树的学习最耗时的一个步骤就是对特征的值进行排序（因为要确定最佳分割点），xgboost在训练之前，预先对数据进行了排序，然后保存为block结构，后面的迭代中重复地使用这个结构，大大减小计算量。这个block结构也使得并行成为了可能，在进行节点的分裂时，需要计算每个特征的增益，最终选增益最大的那个特征去做分裂，那么各个特征的增益计算就可以开多线程进行。
  可并行的近似直方图算法。树节点在进行分裂时，我们需要计算每个特征的每个分割点对应的增益，即用贪心法枚举所有可能的分割点。当数据无法一次载入内存或者在分布式情况下，贪心算法效率就会变得很低，所以xgboost还提出了一种可并行的近似直方图算法，用于高效地生成候选的分割点。

3. 高度的灵活性

• XGBoost 允许用户定义自定义优化目标和评价标准
• 它对模型增加了一个全新的维度，所以我们的处理不会受到任何限制。

4. 缺失值处理

• XGBoost内置处理缺失值的规则。
• 用户需要提供一个和其它样本不同的值，然后把它作为一个参数传进去，以此来作为缺失值的取值。XGBoost在不同节点遇到缺失值时采用不同的处理方法，并且会学习未来遇到缺失值时的处理方法。

5. 剪枝

• 当分裂时遇到一个负损失时，GBM会停止分裂。因此GBM实际上是一个贪心算法。
• XGBoost会一直分裂到指定的最大深度(max_depth)，然后回过头来剪枝。如果某个节点之后不再有正值，它会去除这个分裂。
• 这种做法的优点，当一个负损失（如-2）后面有个正损失（如+10）的时候，就显现出来了。GBM会在-2处停下来，因为它遇到了一个负值。但是XGBoost会继续分裂，然后发现这两个分裂综合起来会得到+8，因此会保留这两个分裂。

6. 内置交叉验证

• XGBoost允许在每一轮boosting迭代中使用交叉验证。因此，可以方便地获得最优boosting迭代次数。
• 而GBM使用网格搜索，只能检测有限个值。

7. 在已有的模型基础上继续

• XGBoost可以在上一轮的结果上继续训练。这个特性在某些特定的应用上是一个巨大的优势。
• sklearn中的GBM的实现也有这个功能，两种算法在这一点上是一致的。

sklearn中的one-hoting编码和pandas的get_dummies()

sklearn.preprocessing 下的 OneHotEncoder 不可以直接处理 string，如果数据集中的某些特征是 string 类型的话，需要首先将其转换为 integers 类型；

在新版本中 sklearn 中，OneHotEncoder 实例的 fit 方法将不再接收 1 维数组，而必须是显式的二维形式；

encoder = OneHotEncoder()
encoder.fit([[1, 2], [2, 1]])

pd.get_dummies()，则恰将 string 转换为 integers 类型：

pd.get_dummies()，则恰将 string 转换为 integers 类型：

pd.get_dummies(['A', 'B', 'A'])
   A  B
0  1  0
1  0  1
2  1  0

xgboost和lightgbm

xgboost和lightgbm支持缺失值处理，不过后者也支持类别特征处理，不需要进行one-hot encoding。

LightGBM优点如下

1. 速度提升 减少内存使用

XGBoost使用基于预排序的算法，难以优化。

LightGBM使用基于直方图的算法，将连续特征离散化，来提升速度，减少内存使用。LightGBM在速度与内存方面的具体优点为

• 减少计算split gain的成本

• 使用直方图减法来提升速度

• 减少内存使用

• 减少并行计算通信成本

2. 适用于稀疏数据

只需O(2 * #non_zero_data)来为稀疏特征构建直方图

3. 准确率提升

• LightGBM采用Leaf-wise (Best-first) 树增长方式

大部分gradient boosting machine算法采用level(depth)-wise树增长方式，如下图

LightGBM采用Leaf-wise (Best-first) 树增长方式，如下图

Leaf-wise (Best-first) 算法选择使得loss下降最快的方式来生长叶子。达到相同叶子数的时候，leaf-wise算法比level-wise算法loss下降得更多。

当数据量太小时，Leaf-wise算法会过拟合，LightGBM使用数最大深度参数来防止过拟合。

• 针对categorical特征优化split

我们经常对categorical特征进行one-hot编码，但这在树学习中并不好，因为对于可取值众多的categorical特征，学习到的树模型会非常不平衡，树深度需要很深才能达到好的准确率。

解决方法是：将categorical特征分成两部分，有 种可能划分，存在算法在 时间内找到最优划分。基本思想是将categorical特征根据与训练目标的相关度进行排序，更具体的，将categorical特征的直方图根据 值进行排序。

4. 网络通信优化

使用collective通信方法，包括”All reduce”, “All gather” and “Reduce scatter”，比点对点通信方法有更好效果。

5. 并行学习优化

• 特征并行
• 数据并行
• 投票并行

6. 支持GPU

7. 应用广泛

• regression, the objective function is L2 loss
• binary classification, the objective function is logloss
• multi classification
• lambdarank, the objective function is lambdarank with NDCG

k-means算法时间复杂度

从算法过程中可以看到，需要求n个数据点和k个中心的距离，外面有多次迭代，迭代次数为m。则k-means算法的时间复杂度为：
O(mnkd)，m与数据集本身的分布情况和初始中心点位置有关。n为数据集中数据样本数量，k为聚类个数，d为数据的维数。

空间复杂度：O((n+k)d)，其中，k为簇的数目，n为样本数，d为维数

马氏距离和欧氏距离

欧氏距离具有平移和旋转不变形

马氏距离除具有平移和旋转不变性外，还具有尺度不变形，并且不受量纲影响。

马氏距离（Mahalanobis Distance）是由印度统计学家马哈拉诺比斯（P. C. Mahalanobis）提出的，表示数据的协方差距离。它是一种有效的计算两个未知样本集的相似度的方法。与欧氏距离不同的是它考虑到各种特性之间的联系并且是尺度无关的（scale-invariant），即独立于测量尺度。

对于一个均值为
$$\mu =({\mu }_1,{\mu }_2,{\mu }_3,...,{\mu }_p{)}^T$$
协方差矩阵为∑的多变量
$$x=(x_1,x_2,x_3,...,x_p{)}^T$$
其马氏距离为：
$$D_M(x)=\sqrt{(x-\mu {)}^T{\sum }^{-1}(x-\mu )}$$

Dropout

训练时

测试时

预测模型的时候，每一个神经单元的权重参数要乘以概率p。

测试阶段Dropout公式：

如何理解

• 组合派

大规模神经网络有两个缺点：费时、容易过拟合。dropout可以使网络变简单，得到更“瘦”的网络

• 动机论

减弱了神经元节点间的联合适应性，增强了泛化能力

• 噪声派

对于每一个dropout后的网络，进行训练时，相当于做了Data Augmentation，因为，总可以找到一个样本，使得在原始的网络上也能达到dropout单元后的效果。 比如，对于某一层，dropout一些单元后，形成的结果是(1.5,0,2.5,0,1,2,0)，其中0是被drop的单元，那么总能找到一个样本，使得结果也是如此。这样，每一次dropout其实都相当于增加了样本。

需要注意的几点

• 经过交叉验证，隐含节点dropout率等于0.5的时候效果最好，原因是0.5的时候dropout随机生成的网络结构最多

• 数据量小的时候，dropout效果不好，数据量大了，dropout效果好

• dropout自己虽然也很牛，但是dropout、max-normalization、large decaying learning rates and high momentum组合起来效果更好，比如max-norm regularization就可以防止大的learning rate导致的参数blow up。

• 缺点是训练时长变长了

Batch Normalization

尽管随机梯度下降对于训练深度神经网络简单高效，但是有很多参数需要人为的调整，比如学习率、参数初始化、权重衰减系数、Dropout比例等等。BN的提出就是为了克服深度神经网络难以训练的弊病。

BN的强大之处在于

• 可以选择较大的初始学习率
• 不用理会过拟合的dropout、L2正则化的参数
• 可以把训练数据打乱

神经网络的本质是学习数据的分布，但是除了输入层的数据(已经归一化)意外，后面每一层的输入数据分布是一直变化的，称为"Internal Covariate Shift"（ICS）现象。

Internal Covariate Shift会带来什么问题？

• 上层网络需要不停调整来适应输入数据分布的变化，导致网络学习速度的降低
• 网络的训练过程容易陷入梯度饱和区，减缓网络收敛速度

covariate shift可以用这么简单的方法解决，那前人对其的研究也真真是白做了。此外，试想，均值方差一致的分布就是同样的分布吗？当然不是。BN到底是什么原理呢？说到底还是为了防止“梯度弥散”。关于梯度弥散，大家都知道一个简单的栗子：。在BN中，是通过将activation规范为均值和方差一致的手段使得原本会减小的activation的scale变大。

BN详细过程

测试阶段如何使用Batch Normalization？

我们知道BN在每一层计算的$\mu$ 与${\sigma }^2$ 都是基于当前batch中的训练数据，但是这就带来了一个问题：我们在预测阶段，有可能只需要预测一个样本或很少的样本，没有像训练样本中那么多的数据，此时$\mu$ 与${\sigma }^2$的计算一定是有偏估计，这个时候我们该如何进行计算呢？
利用BN训练好模型后，我们保留了每组mini-batch训练数据在网络中每一层的${\mu }_{batch}$ 与${\sigma }_{batch}^2$ 。此时我们使用整个样本的统计量来对Test数据进行归一化，具体来说使用均值与方差的无偏估计：
$${\mu }_{test}=E({\mu }_{batch})$$

$${\sigma }_{test}^2=\frac{m}{m-1}E({\sigma }_{batch}^2)$$

得到每个特征的均值与方差的无偏估计后，我们对test数据采用同样的normalization方法：
$$BN(X_{test})=\gamma \ast \frac{X_{test}-{\mu }_{test}}{\sqrt{{\sigma }_{test}^2+ϵ}}+\beta$$

另外，除了采用整体样本的无偏估计外。吴恩达在Coursera上的Deep Learning课程指出可以对train阶段每个batch计算的mean/variance采用指数加权平均来得到test阶段mean/variance的估计。

深度学习调参技巧

训练技巧对深度学习来说是非常重要的，作为一门实验性质很强的科学，同样的网络结构使用不同的训练方法训练，结果可能会有很大的差异。这里我总结了近一年来的炼丹心得，分享给大家，也欢迎大家补充指正。

参数初始化

下面几种方式,随便选一个,结果基本都差不多。但是一定要做。否则可能会减慢收敛速度，影响收敛结果，甚至造成Nan等一系列问题。

下面的n_in为网络的输入大小，n_out为网络的输出大小，n为n_in或(n_in+n_out)*0.5

Xavier初始法论文：http://jmlr.org/proceedings/papers/v9/glorot10a/glorot10a.pdf

He初始化论文：https://arxiv.org/abs/1502.01852

• uniform均匀分布初始化： w = np.random.uniform(low=-scale, high=scale, size=[n_in,n_out])

• • Xavier初始法，适用于普通激活函数(tanh,sigmoid)：scale = np.sqrt(3/n)
  • He初始化，适用于ReLU：scale = np.sqrt(6/n)

• normal高斯分布初始化： w = np.random.randn(n_in,n_out) * stdev # stdev为高斯分布的标准差，均值设为0

• • Xavier初始法，适用于普通激活函数 (tanh,sigmoid)：stdev = np.sqrt(n)
  • He初始化，适用于ReLU：stdev = np.sqrt(2/n)

• svd初始化：对RNN有比较好的效果。参考论文：https://arxiv.org/abs/1312.6120

数据预处理方式

• zero-center ,这个挺常用的. X -= np.mean(X, axis = 0) # zero-center X /= np.std(X, axis = 0) # normalize
• PCA whitening,这个用的比较少.

训练技巧

• 要做梯度归一化,即算出来的梯度除以minibatch size
• clip (梯度裁剪): 限制最大梯度,其实是value = sqrt(w1^2+w22….),如果value超过了阈值,就算一个衰减系系数,让value的值等于阈值: 5,10,15
• dropout对小数据防止过拟合有很好的效果,值一般设为0.5,小数据上dropout+sgd在我的大部分实验中，效果提升都非常明显.因此可能的话，建议一定要尝试一下。 dropout的位置比较有讲究, 对于RNN,建议放到输入->RNN与RNN->输出的位置.关于RNN如何用dropout,可以参考这篇论文:http://arxiv.org/abs/1409.2329
• adam,adadelta等,在小数据上,我这里实验的效果不如sgd, sgd收敛速度会慢一些，但是最终收敛后的结果，一般都比较好。如果使用sgd的话,可以选择从1.0或者0.1的学习率开始,隔一段时间,在验证集上检查一下,如果cost没有下降,就对学习率减半. 我看过很多论文都这么搞,我自己实验的结果也很好. 当然,也可以先用ada系列先跑,最后快收敛的时候,更换成sgd继续训练.同样也会有提升.据说adadelta一般在分类问题上效果比较好，adam在生成问题上效果比较好。
• 除了gate之类的地方,需要把输出限制成0-1之外,尽量不要用sigmoid,可以用tanh或者relu之类的激活函数.1. sigmoid函数在-4到4的区间里，才有较大的梯度。之外的区间，梯度接近0，很容易造成梯度消失问题。2. 输入0均值，sigmoid函数的输出不是0均值的。
• rnn的dim和embdding size,一般从128上下开始调整. batch size,一般从128左右开始调整.batch size合适最重要,并不是越大越好.
• word2vec初始化,在小数据上,不仅可以有效提高收敛速度,也可以可以提高结果.
• 尽量对数据做shuffle
• LSTM 的forget gate的bias,用1.0或者更大的值做初始化,可以取得更好的结果,来自这篇论文:http://jmlr.org/proceedings/papers/v37/jozefowicz15.pdf, 我这里实验设成1.0,可以提高收敛速度.实际使用中,不同的任务,可能需要尝试不同的值.
• Batch Normalization据说可以提升效果，不过我没有尝试过，建议作为最后提升模型的手段，参考论文：Accelerating Deep Network Training by Reducing Internal Covariate Shift
• 如果你的模型包含全连接层（MLP），并且输入和输出大小一样，可以考虑将MLP替换成Highway Network,我尝试对结果有一点提升，建议作为最后提升模型的手段，原理很简单，就是给输出加了一个gate来控制信息的流动，详细介绍请参考论文: http://arxiv.org/abs/1505.00387
• 来自@张馨宇的技巧：一轮加正则，一轮不加正则，反复进行。

Ensemble

Ensemble是论文刷结果的终极核武器,深度学习中一般有以下几种方式

• 同样的参数,不同的初始化方式
• 不同的参数,通过cross-validation,选取最好的几组
• 同样的参数,模型训练的不同阶段，即不同迭代次数的模型。
• 不同的模型,进行线性融合. 例如RNN和传统模型.

梯度消失、爆炸的解决方案

方案1-预训练加微调

此方法来自Hinton在2006年发表的一篇论文，Hinton为了解决梯度的问题，提出采取无监督逐层训练方法，其

基本思想是每次训练一层隐节点，训练时将上一层隐节点的输出作为输入，而本层隐节点的输出作为下一层隐节

点的输入，此过程就是逐层“预训练”（pre-training）；在预训练完成后，再对整个网络进行“微调”（fine-

tunning）。Hinton在训练深度信念网络（Deep Belief Networks中，使用了这个方法，在各层预训练完成后，

再利用BP算法对整个网络进行训练。此思想相当于是先寻找局部最优，然后整合起来寻找全局最优，此方法有一

定的好处，但是目前应用的不是很多了。

方案2-梯度剪切、正则

梯度剪切这个方案主要是针对梯度爆炸提出的，其思想是设置一个梯度剪切阈值，然后更新梯度的时候，如果梯

度超过这个阈值，那么就将其强制限制在这个范围之内。这可以防止梯度爆炸。

另外一种解决梯度爆炸的手段是采用权重正则化（weithts regularization）比较常见的是L1正则，和L2正则，

在各个深度框架中都有相应的API可以使用正则化。

方案3-relu、leakrelu、elu等激活函数

Relu

思想也很简单，如果激活函数的导数为1，那么就不存在梯度消失爆炸的问题了，每层的网络都可以得到相同的更新速度，relu就这样应运而生。
relu函数的导数在正数部分是恒等于1的，因此在深层网络中使用relu激活函数就不会导致梯度消失和爆炸的问题。
relu的主要贡献在于：
（1）解决了梯度消失、爆炸的问题
（2）计算方便，计算速度快
（3）加速了网络的训练

同时也存在一些缺点：
（1）由于负数部分恒为0，会导致一些神经元无法激活（可通过设置小学习率部分解决）；
（2）输出不是以0为中心的。

leakrelu

leakrelu就是为了解决relu的0区间带来的影响，其数学表达为：leak_relu$=max(k\ast x,0)$其中$k$是leak系数，一般选择$0.01$或者$0.02$，或者通过学习而来。

方案4-BatchNorm

BatchNorm是深度学习发展以来提出的最重要的成果之一了，目前已经被广泛的应用到了各大网络中，具有加速网络收敛速度，提升训练稳定性的效果，BatchNorm本质上是解决反向传播过程中的梯度问题。BatchNorm全名是Batch Normalization，简称BN，即批规范化，通过规范化操作将输出信号$x$规范化到均值为$0$，方差为$1$保证网络的稳定性。

方案5-残差结构

事实上，就是残差网络的出现导致了Imagenet比赛的终结，自从残差提出后，几乎所有的深度网络都离不开残差

的身影，相比较之前的几层，几十层的深度网络，在残差网络面前都不值一提，残差可以很轻松的构建几百层，

一千多层的网络而不用担心梯度消失过快的问题，原因就在于残差的捷径（shortcut）部分。

方案6-LSTM
LSTM全称是长短期记忆网络（long-short term memory networks），是不那么容易发生梯度消失的，主要原

因在于LSTM内部复杂的“门”(gates)。

微调有哪些不同方法？

​ 以图像分类为例，通常情况下由于不同数据集需要的类别数不同，我们需要修改网络的输出顶层。这种情况下有两种微调方式：

• 不冻结网络模型的任何层，对最后的改动层使用较大的学习率，对未改动层以较小的学习率进行训练全模型训练，进行多轮训练即可。即一步完成训练。
• 冻结除了顶部改动层以外的所有层参数，即不对冻结部分的层进行参数训练更新，进行若干轮的微调训练后，放开顶部层以下的若干层或者全部放开所有层的参数，再次进行若干轮训练即可。即分多步训练。

​ 以上两种都属于微调。目前由于存在大量优秀的预训练模型，如何确定哪个模型适合自己的任务并能得到最佳性能需要花大量的时间探索。此时，上述的前者是种不错训练方式，你无须进行过多分步的操作。而当探索到一个比较适合的模型时，你不妨可以再次重新尝试下以第二种方式进行训练，或许能得到相比于前者稍高些的性能，因为小数据集上调整过多的参数过拟合的机率也会增大，当然这并不是绝对的。

微调先冻结底层，训练顶层的原因？

​ 14.10中第二种冻结多步训练的方式。首先冻结除了顶部改动层以外的所有层参数，对顶层进行训练，这个过程可以理解为顶层的域适应训练，主要用来训练适应模型的现有特征空间，防止顶层糟糕的初始化，对已经具备一定表达能力的层的干扰和破坏，影响最终的性能。之后，在很多深度学习框架教程中会使用放开顶层往下一半的层数，继续进行微调。这样的好处在于越底层的特征通常是越通用的特征，越往上其整体的高层次语义越完备，这通过感受野很容易理解。所以，若预训练模型的数据和微调训练的数据语义差异越大（例如ImageNet的预模型用于医学图像的训练），那越往顶层的特征语义差异就越大，因此通常也需要进行相应的调整。

不同的数据集特性下如何微调？

• 数据集数据量少，数据和原数据集类似。这是通常做法只需修改最后的输出层，训练即可，训练过多参数容易过拟合。
• 数据集数据量少，数据和原数据集差异较大。由于数据差异较大，可以在完成输出顶层的微调后，微调顶层往下一半的层数，进行微调，原因见14.11。
• 数据集数据量大，数据与原数据集差异较大。这种情况下，通常已经不需要用预训练模型进行微调，通常直接重新训练即可。
• 数据集数据量大，数据与原数据类似。这时预训练模型的参数是个很好的初始化，可利用预训练模型放开所有层以较小的学习率微调即可。

为什么RNN使用tanh不使用ReLU？

对CNN来说，使用sigmoid作为激活函数的话，导数在(0, 0,25]之间，小于1的数乘在一起，必然是越乘越小的，自然会导致梯度消失。而ReLU的导数为{0，1}，这样的话只要一条路径上的导数都是1，无论神经网络是多少层，这一部分的乘积都始终为1，因此深层的梯度也可以传递到浅层中。

而对RNN来说，如果使用ReLU，会导致非常大的输出值。
$$a_i=W{f}_{i-1}+U{x}_i+b_i$$

$$f_i=f[a_i]$$

在这个表示中，RNN每个阶段的输入是 $x_i$，和CNN每一层使用独立的参数$W_i$不同，原始的RNN在每个阶段都共享一个参数 $W$。如果我们假设从某一层开始输入$x_i$和偏置$b_i$ 都为0，那么最后得到的输出就是
$$f[W...[Wf[Wf[Wf[W{f}_i]]]]]$$

这在某种程度上相当于对参数矩阵$W$ 作连乘，很显然，只要 $W$有一个大于1的特征值，在经过若干次连乘后都会导致结果是一个数值非常庞大的矩阵。

另外一方面，将激活函数换成ReLU也不能解决梯度在长程上传递的问题，因为CNN中，每一层的参数是相互独立的，并且都是系数矩阵，进行连乘也不会导致梯度爆炸，而RNN中W参与了每个时间段的运算，连乘的话很容易导致梯度爆炸/消失问题。

一元线性回归的基本假设有：

（1）随机误差项是一个期望值或平均值为0的随机变量；

（2）对于解释变量的所有观测值，随机误差项有相同的方差；

（3）随机误差项彼此不相关；

（4）解释变量是确定性变量，不是随机变量，与随机误差项彼此之间相互独立；

（5）解释变量之间不存在精确的（完全的）线性关系，即解释变量的样本观测值矩阵是满秩矩阵；

（6）随机误差项服从正态分布

所谓多重共线性（Multicollinearity）是指线性回归模型中的解释变量之间由于存在精确相关关系或高度相关关系而使模型估计失真或难以估计准确。

神经网络中激活函数的意义？

一个激活函数需要具有哪些必要的属性？还有哪些属是好的属性但不必要的？

1. 非线性：即导数不是常数。这个条件前面很多答主都提到了，是多层神经网络的基础，保证多层网络不退化成单层线性网络。这也是激活函数的意义所在。

2. 几乎处处可微：可微性保证了在优化中梯度的可计算性。传统的激活函数如sigmoid等满足处处可微。对于分段线性函数比如ReLU，只满足几乎处处可微（即仅在有限个点处不可微）。对于SGD算法来说，由于几乎不可能收敛到梯度接近零的位置，有限的不可微点对于优化结果不会有很大影响。

3. 计算简单：正如题主所说，非线性函数有很多。极端的说，一个多层神经网络也可以作为一个非线性函数，类似于Network In Network中把它当做卷积操作的做法。但激活函数在神经网络前向的计算次数与神经元的个数成正比，因此简单的非线性函数自然更适合用作激活函数。这也是ReLU之流比其它使用Exp等操作的激活函数更受欢迎的其中一个原因。

4. 非饱和性（saturation）：饱和指的是在某些区间梯度接近于零（即梯度消失），使得参数无法继续更新的问题。最经典的例子是Sigmoid，它的导数在x为比较大的正值和比较小的负值时都会接近于0。更极端的例子是阶跃函数，由于它在几乎所有位置的梯度都为0，因此处处饱和，无法作为激活函数。ReLU在x>0时导数恒为1，因此对于再大的正值也不会饱和。但同时对于x<0，其梯度恒为0，这时候它也会出现饱和的现象（在这种情况下通常称为dying ReLU）。Leaky ReLU[3]和PReLU的提出正是为了解决这一问题。

5. 单调性（monotonic）：即导数符号不变。这个性质大部分激活函数都有，除了诸如sin、cos等。个人理解，单调性使得在激活函数处的梯度方向不会经常改变，从而让训练更容易收敛。

6. 输出范围有限：有限的输出范围使得网络对于一些比较大的输入也会比较稳定，这也是为什么早期的激活函数都以此类函数为主，如Sigmoid、Tanh。但这导致了前面提到的梯度消失问题，而且强行让每一层的输出限制到固定范围会限制其表达能力。因此现在这类函数仅用于某些需要特定输出范围的场合，比如概率输出（此时loss函数中的log操作能够抵消其梯度消失的影响）、LSTM里的gate函数。

7. 接近恒等变换（identity）：即约等于x。这样的好处是使得输出的幅值不会随着深度的增加而发生显著的增加，从而使网络更为稳定，同时梯度也能够更容易地回传。这个与非线性是有点矛盾的，因此激活函数基本只是部分满足这个条件，比如Tanh只在原点附近有线性区（在原点为0且在原点的导数为1），而ReLU只在x>0时为线性。这个性质也让初始化参数范围的推导更为简单。额外提一句，这种恒等变换的性质也被其他一些网络结构设计所借鉴，比如CNN中的ResNet和RNN中的LSTM。

8. 参数少：大部分激活函数都是没有参数的。像PReLU带单个参数会略微增加网络的大小。还有一个例外是Maxout，尽管本身没有参数，但在同样输出通道数下k路Maxout需要的输入通道数是其它函数的k倍，这意味着神经元数目也需要变为k倍；但如果不考虑维持输出通道数的情况下，该激活函数又能将参数个数减少为原来的k倍。

9. 归一化（normalization）：这个是最近才出来的概念，对应的激活函数是SELU，主要思想是使样本分布自动归一化到零均值、单位方差的分布，从而稳定训练。在这之前，这种归一化的思想也被用于网络结构的设计，比如Batch Normalization。

Weight Normalization和Batch Normalization

答案来源：Weight Normalization 相比batch Normalization 有什么优点呢？

Weight Normalization 和 Batch Normalization 都属于参数重写（Reparameterization）的方法，只是采用的方式不同，Weight Normalization 是对网络权值$W$ 进行 normalization，因此也称为 Weight Normalization；Batch Normalization 是对网络某一层输入数据进行 normalization。Weight Normalization相比Batch Normalization有以下三点优势：

1. Weight Normalization 通过重写深度学习网络的权重W的方式来加速深度学习网络参数收敛，没有引入 minbatch 的依赖，适用于 RNN（LSTM）网络（Batch Normalization 不能直接用于RNN，进行 normalization 操作，原因在于：1) RNN 处理的 Sequence 是变长的；2) RNN 是基于 time step 计算，如果直接使用 Batch Normalization 处理，需要保存每个 time step 下，mini btach 的均值和方差，效率低且占内存）。
2. Batch Normalization 基于一个 mini batch 的数据计算均值和方差，而不是基于整个 Training set 来做，相当于进行梯度计算式引入噪声。因此，Batch Normalization 不适用于对噪声敏感的强化学习、生成模型（Generative model：GAN，VAE）使用。相反，Weight Normalization 对通过标量 $g$ 和向量 $v$ 对权重 $W$ 进行重写，重写向量 $v$ 是固定的，因此，基于 Weight Normalization 的 Normalization 可以看做比 Batch Normalization 引入更少的噪声。
3. 不需要额外的存储空间来保存 mini batch 的均值和方差，同时实现 Weight Normalization 时，对深度学习网络进行正向信号传播和反向梯度计算带来的额外计算开销也很小。因此，要比采用 Batch Normalization 进行 normalization 操作时，速度快。 但是 Weight Normalization 不具备 Batch Normalization 把网络每一层的输出 Y 固定在一个变化范围的作用。因此，采用 Weight Normalization 进行 Normalization 时需要特别注意参数初始值的选择。

EM算法、HMM、CRF

这三个放在一起不是很恰当，但是有互相有关联，所以就放在这里一起说了。注意重点关注算法的思想。
（1）EM算法
EM算法是用于含有隐变量模型的极大似然估计或者极大后验估计，有两步组成：E步，求期望（expectation）；M步，求极大（maxmization）。本质上EM算法还是一个迭代算法，通过不断用上一代参数对隐变量的估计来对当前变量进行计算，直到收敛。
注意：EM算法是对初值敏感的，而且EM是不断求解下界的极大化逼近求解对数似然函数的极大化的算法，也就是说EM算法不能保证找到全局最优值。对于EM的导出方法也应该掌握。
（2）HMM算法
隐马尔可夫模型是用于标注问题的生成模型。有几个参数（π，A，B）：初始状态概率向量π，状态转移矩阵A，观测概率矩阵B。称为马尔科夫模型的三要素。

马尔科夫三个基本问题：

• 概率计算问题：给定模型和观测序列，计算模型下观测序列输出的概率。–> 前向后向算法
• 学习问题：已知观测序列，估计模型参数，即用极大似然估计来估计参数。–> Baum-Welch(也就是EM算法)和极大似然估计。
• 预测问题：已知模型和观测序列，求解对应的状态序列。-> 近似算法（贪心算法）和维比特算法（动态规划求最优路径）

（3）条件随机场CRF
　给定一组输入随机变量的条件下另一组输出随机变量的条件概率分布密度。条件随机场假设输出变量构成马尔科夫随机场，而我们平时看到的大多是线性链条随机场，也就是由输入对输出进行预测的判别模型。求解方法为极大似然估计或正则化的极大似然估计。
　之所以总把HMM和CRF进行比较，主要是因为CRF和HMM都利用了图的知识，但是CRF利用的是马尔科夫随机场（无向图），而HMM的基础是贝叶斯网络（有向图）。而且CRF也有：概率计算问题、学习问题和预测问题。大致计算方法和HMM类似，只不过不需要EM算法进行学习问题。

（4）HMM和CRF对比
　其根本还是在于基本的理念不同，一个是生成模型，一个是判别模型，这也就导致了求解方式的不同。

CNN常用的几个模型

名称	特点
LeNet5	没啥特点-不过是第一个CNN应该要知道
AlexNet	引入了ReLU和dropout，引入数据增强、池化相互之间有覆盖，三个卷积一个最大池化+三个全连接层
VGGNet	采用1×1和3×3的卷积核以及2×2的最大池化使得层数变得更深。常用VGGNet-16和VGGNet19
Google Inception Net	这个在控制了计算量和参数量的同时，获得了比较好的分类性能，和上面相比有几个大的改进： 1、去除了最后的全连接层，而是用一个全局的平均池化来取代它； 2、引入Inception Module，这是一个4个分支结合的结构。所有的分支都用到了1×1的卷积，这是因为1×1性价比很高，可以用很少的参数达到非线性和特征变换。 3、Inception V2第二版将所有的5×5变成2个3×3，而且提出来著名的Batch Normalization； 4、Inception V3第三版就更变态了，把较大的二维卷积拆成了两个较小的一维卷积，加速运算、减少过拟合，同时还更改了Inception Module的结构。
ResNet残差神经网络	1、引入高速公路结构，可以让神经网络变得非常深 2、ResNet第二个版本将ReLU激活函数变成y=x的线性函数

CNN对位移、尺度和旋转不变性的讨论

CNN得益于全局共享权值和pool操作，具有平移不变性。

对于尺度不变性，是没有或者说具有一定的不变性（尺度变化不大），实验中小目标的检测是难点，需要采用FPN或者其他的方式单独处理。

对于旋转不变性，是基本没有的，实验证明添加旋转样本是一种可靠的样本增强策略，能增强模型对旋转的鲁棒性。只能通过data argumentation这种方式（人为地对样本做 镜像、旋转、缩放等操作）让CNN自己去学习旋转不变性。

data augmentation 几种方法总结

在深度学习中，有的时候训练集不够多，或者某一类数据较少，或者为了防止过拟合，让模型更加鲁棒性，data augmentation是一个不错的选择。

常见方法

Color Jittering：对颜色的数据增强：图像亮度、饱和度、对比度变化（此处对色彩抖动的理解不知是否得当）；

PCA Jittering：首先按照RGB三个颜色通道计算均值和标准差，再在整个训练集上计算协方差矩阵，进行特征分解，得到特征向量和特征值，用来做PCA Jittering；

Random Scale：尺度变换；

Random Crop：采用随机图像差值方式，对图像进行裁剪、缩放；包括Scale Jittering方法（VGG及ResNet模型使用）或者尺度和长宽比增强变换；

Horizontal/Vertical Flip：水平/垂直翻转；

Shift：平移变换；

Rotation/Reflection：旋转/仿射变换；

Noise：高斯噪声、模糊处理；

Label shuffle：类别不平衡数据的增广，参见海康威视ILSVRC2016的report；另外，文中提出了一种Supervised Data Augmentation方法，有兴趣的朋友的可以动手实验下。

感受野的计算

$$R{F}_k=R{F}_{k-1}+((kernalsiz{e}_k-1)\prod _{i-1}^{k-1}strid{e}_i)$$

下面是一个计算例子

Layer #	Kernel Size	Stride	Dilation	Padding	Input Size	Output Size	Receptive Field
1	3	1	1	0	256	254	3
2	2	2	1	0	254	127	4
3	3	1	1	0	127	125	8
4	2	2	1	0	125	62	10
5	3	1	1	0	62	60	18
6	3	1	1	0	60	58	26
7	2	2	1	0	58	29	30

$$\begin{gathered} R{F}_0=1 \\ R{F}_1=1+(3-1)=3 \\ R{F}_2=3+(2-1)\ast 2=4 \\ R{F}_3=4+(3-1)\ast 1\ast 2=8 \\ R{F}_4=8+(2-1)\ast 1\ast 2=10 \end{gathered}$$

一个计算感受野的网站

逻辑回归相关问题

（1）公式推导一定要会

（2）逻辑回归的基本概念
　　这个最好从广义线性模型的角度分析，逻辑回归是假设y服从Bernoulli分布。

（3）L1-norm和L2-norm
　　其实稀疏的根本还是在于L0-norm也就是直接统计参数不为0的个数作为规则项，但实际上却不好执行于是引入了L1-norm；而L1norm本质上是假设参数先验是服从Laplace分布的，而L2-norm是假设参数先验为Gaussian分布，我们在网上看到的通常用图像来解答这个问题的原理就在这。
　　但是L1-norm的求解比较困难，可以用坐标轴下降法或是最小角回归法求解。

（4）LR和SVM对比
　　首先，LR和SVM最大的区别在于损失函数的选择，LR的损失函数为Log损失（或者说是逻辑损失都可以）、而SVM的损失函数为hinge loss。

其次，两者都是线性模型。

最后，SVM只考虑支持向量（也就是和分类相关的少数点）

（5）LR和随机森林区别
　　随机森林等树算法都是非线性的，而LR是线性的。LR更侧重全局优化，而树模型主要是局部的优化。

（6）常用的优化方法
　　逻辑回归本身是可以用公式求解的，但是因为需要求逆的复杂度太高，所以才引入了梯度下降算法。

一阶方法：梯度下降、随机梯度下降、mini 随机梯度下降法。

二阶方法：牛顿法、拟牛顿法：

这里详细说一下牛顿法的基本原理和牛顿法的应用方式。牛顿法其实就是通过切线与x轴的交点不断更新切

线的位置，直到达到曲线与x轴的交点得到方程解。在实际应用中我们因为常常要求解凸优化问题，也就是要求

解函数一阶导数为0的位置，而牛顿法恰好可以给这种问题提供解决方法。实际应用中牛顿法首先选择一个点作

为起始点，并进行一次二阶泰勒展开得到导数为0的点进行一个更新，直到达到要求，这时牛顿法也就成了二阶

求解问题，比一阶方法更快。我们常常看到的x通常为一个多维向量，这也就引出了Hessian矩阵的概念（就是x

的二阶导数矩阵）。

缺点：牛顿法是定长迭代，没有步长因子，所以不能保证函数值稳定的下降，严重时甚至会失败。还有就是牛顿

法要求函数一定是二阶可导的。而且计算Hessian矩阵的逆复杂度很大。

拟牛顿法： 不用二阶偏导而是构造出Hessian矩阵的近似正定对称矩阵的方法称为拟牛顿法。拟牛顿法的思路就

是用一个特别的表达形式来模拟Hessian矩阵或者是他的逆使得表达式满足拟牛顿条件。主要有DFP法（逼近

Hessian的逆）、B-FGS（直接逼近Hessian矩阵）、 L-BFGS（可以减少B-FGS所需的存储空间）。

简述梯度下降法、牛顿法与共轭梯度法的原理，并比较异同点及各自的使用范围。

\1. 算法原理

​ 梯度下降法是利用一阶的梯度信息找到函数局部最优解的一种方法。如果目标函数是一个凸优化问题，那么梯度下降法获得的局部最优解就是全局最优解。

​ 牛顿法是利用局部的一阶和二阶偏导信息，去推测整个目标函数的形状，进而可以求得近似函数的全局最小值，然后将当前的最小值设定为近似函数的最小值。也就是说，牛顿法在二阶导数的作用下，从函数的凸性出发，直接搜索怎样到达极值点，即在选择方向时，不仅考虑当前坡度是否够大，还会考虑走了一步之后，坡度是否会变得更大。

​ 共轭梯度法是介于最速下降法与牛顿法之间的一个方法，它仅需一阶导数信息。基本思想是把共轭性与最速下降法相结合，利用已知点处的梯度构造一组共轭方向，并沿这组方向进行搜索，求出目标函数的极小点。根据共轭方向的基本性质，这种方法具有二次终止性。核心迭代过程可以采取不同的方案，一种是直接延续，即总是用
$$d^{(k+1)}=-g(k+1)+{\beta }_k\ast d^{(k)}$$
构造搜索方向；一种是把n步作为一轮，每搜索一轮之后，取一次最速下降方向，开始下一轮，此种策略称为“重置”。

\2. 比较异同点
共轭梯度法仅需一阶导数信息，克服了最速下降法收敛慢的缺点，又避免了牛顿法需要存储和计算Hesse矩阵并求逆的缺点。

​ 牛顿法和梯度下降法都必须给定一个初始点，且都容易陷入局部最优。但在初始点选取合理的情况下，牛顿法比梯度下降法收敛速度更快。

​ 牛顿法需要利用二阶导数信息，每次需要更新一个二维矩阵，计算难度和资源消耗相对梯度下降和共轭法都要更大，实际使用中常使用拟牛顿法。

​ 牛顿法对初始值有一定要求，在非凸优化问题中（如神经网络训练），牛顿法很容易陷入鞍点（牛顿法步长会越来越小）；而梯度下降法则很容易逃离鞍点（因此在神经网络训练中一般使用梯度下降法，高维空间的神经网络中存在大量鞍点）
​ 梯度下降法在靠近最优点时会震荡，因此步长调整在梯度下降法中是必要的，具体有adagrad, adadelta, rmsprop, adam等一系列自适应学习率的方法。

梯度下降法和牛顿法比较

梯度下降法

在机器学习任务中，需要最小化损失函数$L(\theta )$，其中$\theta$是要求解的模型参数。梯度下降法常用来求解这种无约束最优化问题，它是一种迭代方法：选取初值 ，不断迭代，更新$\theta$的值，进行损失函数的极小化。

• 迭代公式： ${\theta }^t={\theta }^{t-1}+\Delta \theta$
• 将$L({\theta }^t)$在${\theta }^{t-1}$处进行一阶泰勒展开：
  $$L({\theta }^t)=L({\theta }^{t-1}+\Delta \theta )\approx L({\theta }^{t-1})+L^{{}^{\prime }}({\theta }^{t-1})\Delta \theta$$
• 要使得 ，可取$L({\theta }^t)<L({\theta }^{t-1}$，则：
  这里$\alpha$是步长，可通过line search确定，但一般直接赋一个小的数。

牛顿法

牛顿法是二阶泰勒展开。

• 将$L({\theta }^t)$在${\theta }^{t-1}$处进行二阶泰勒展开：
  $$L({\theta }^t)\approx L({\theta }^{t-1})+L^{{}^{\prime }}({\theta }^{t-1})\Delta \theta +\frac{1}{2}{L}^{{}^{\prime \prime }}({\theta }^{t-1})\Delta {\theta }^2$$
  为了简化分析过程，假设参数$\theta$是标量（即 只有一维），则可将一阶和二阶导数分别记为$g$和$h$ ：
  $$L({\theta }^t)\approx L({\theta }^{t-1})+g\Delta \theta +\frac{1}{2}h\Delta {\theta }^2$$
• 要使得$L({\theta }^t)$取得极小值，即让$g\Delta \theta +\frac{1}{2}h\Delta {\theta }^2$极小，令$\frac{\partial (g\Delta \theta +\frac{1}{2}h\Delta {\theta }^2)}{\partial \Delta \theta }$，得到$\Delta \theta =-\frac{g}{h}$，故${\theta }^t={\theta }^{t-1}+\Delta \theta ={\theta }^{t-1}-\frac{g}{h}$
  参数$\theta$推广到向量形式，迭代公式${\theta }^t={\theta }^{t-1}-H^{-1}g$，这里$H$是海森矩阵。

梯度下降法和牛顿法对比

梯度下降是一阶收敛，牛顿法是二阶收敛，所以牛顿法就更快。

如果更通俗地说的话，比如你想找一条最短的路径走到一个盆地的最底部，梯度下降法每次只从你当前所处位置选一个坡度最大的方向走一步；而牛顿法在选择方向时，不仅会考虑坡度是否够大，还会考虑你走了一步之后，坡度是否会变得更大。所以，可以说牛顿法比梯度下降法看得更远一点，能更快地走到最底部。

根据wiki上的解释，从几何上说，牛顿法就是用一个二次曲面去拟合你当前所处位置的局部曲面，而梯度下降法是用一个平面去拟合当前的局部曲面，通常情况下，二次曲面的拟合会比平面更好，所以牛顿法选择的下降路径会更符合真实的最优下降路径。

简述协方差的含义及协方差矩阵的计算过程。

现有m条n列原始数据，试简述利用PCA算法对该数据进行降维的过程。

\1. 协方差就是计算了两个维度之间的相关性，即这个样本的这两个维度之间有没有关系。（2分）

​ 协方差矩阵的计算：
1）先让样本矩阵中心化，即每一维度减去该维度的均值，使每一维度上的均值为0，
2）然后直接用新的到的样本矩阵乘上它的转置
3）然后除以(N-1)即可

\2. 按行或按列组织样本均可。

​ 下面是按行组织样本：

​ 1）将原始数据按行组成n行m列矩阵X，代表有n个数据，每个数据m个特征

​ 2）将X的每一列（代表一个属性字段）进行零均值化，即减去这一列的均值

​ 3）求出协方差矩阵C=1/n* XXT

​ 4）求出协方差矩阵的特征值及对应的特征向量

​ 5）将特征向量按对应特征值大小从上到下按列排列成矩阵，取前k列组成矩阵P

​ 6）Y=XP即为降维到k维后的数据

谈谈广义线性模型在机器学习算法中的应用。

在标准的SVM中，样本会被最优分类面分为+1或-1；而在实际应用中，后验概率是非常有用的。考虑如何使SVM实现后验概率的输出。

\1. 广义线性模型相对于经典的线性模型(y=wx+b)，核心在于引入了连接函数g(.)。

​ 在机器学习中应用广泛，比如逻辑回归中的用sigmoid函数进行转换；在神经网络中的激活函数也是链接函数。

\2. 可以使用Sigmoid函数进行转换，对f(x)（即核函数）设学习参数，即Sigmoid((Af(x)+b))。概率SVM的构造主要分为两个步骤：首先训练标准的SVM模型。得到核函数的参数；其次训练Sigmoid函数，得到Sigmoid的参数。这样就可以对标准的SVM模型的输出值进行Sigmoid处理，将其转化为后验概率。