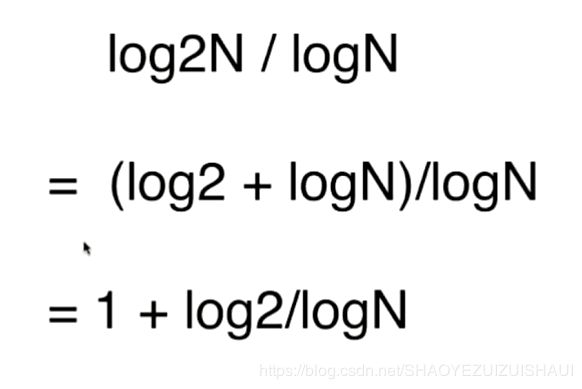二分搜索树
二叉搜索树解决查找这类问题
二分查找法:
对于有序的数列,才能使用二分查找法。
二分查找法的时间复杂度:
此时将时间复杂度称为,logN,如果数据规模N以2倍的速度增加,时间增加会越来越慢,类似于log函数性质,可以利用下面的公式推导
//--------------------二分查找法-------------------------
//在大小为n的T类型的有序数组arr中,查找target
//如果找到target,则返回target的索引值
//如果没找到target,则返回-1
template
int binarySearch(T arr[], int n, T target)
{
//在arr[l...r]数组中查找元素
int l = 0;
int r = n - 1;
while (l <= r)
{
//int mid = (l+r)/ 2;
int mid = l + (r - l) / 2;
if (arr[mid] == target)
return mid;
else if (arr[mid] > target)
//接下来会在arr[mid-1...r]中查找target
r = mid-1;
else
////接下来会在arr[l...mid-1]中查找target
l = mid+1;
}
return -1;
}
template
int __binarySearch_1(T arr[], int l, int r, T target)
{
//在arr[l...r]数组中查找元素
if (l >r)
return -1;
int mid = l + (r - l) / 2;
//cout <
int binarySearch_1(T arr[], int n, T target)
{
//在arr[0...r]数组中查找元素
int r = n - 1;
return __binarySearch_1(arr,0,r,target);
}
//-------------------二分查找法的调试程序(大括号去掉)--------------------
//建立一个int 型的有序数组,传递给二分查找函数
int arr[50];
for (int i=0; i < 50;i++)
{
arr[i] = i ;
}
cout << binarySearch_1(arr, 50, 40) << endl;
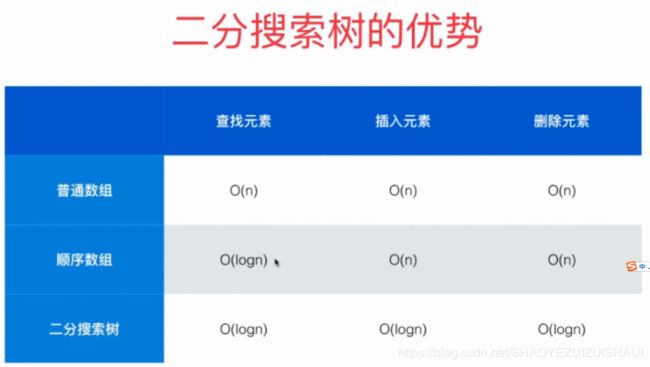
实现查找表最基础的方式,就是实现二分搜索树
顺序数组可以采用二分查找法查找,查找元素O(logN)
二分搜索树不是完全二叉树,所以不同于堆,不采用数组的方式表示,采用节点方式
二分搜索树查找的第一种方式,返回value值
//输入树中各个节点指针,和需要查找的key
//查看以node为根的二叉搜索树中是否包含键值为key的节点
//返回查找的键值的对应的value*
ValueSearch_(Node* node,Key key)
{
if (node == NULL)
return NULL;
//如果相等,则覆盖value
if (node->key == key)
return node->value;
else if (node->key > key)
Search_(node->left, key);
else
Search_(node->right, key);
}
//查找,返回value
Value Search(Key key)
{
return Search_(root, key);
}二分搜索树查找的第二种方式,返回value*,用户可以方便更改查找key的value的值
//输入树中各个节点指针,和需要查找的key
//查看以node为根的二叉搜索树中是否包含键值为key的节点
//返回查找的键值的对应的value*
Value* Search_(Node* node,Key key)
{
if (node == NULL)
return NULL;
//如果相等,则覆盖value
if (node->key == key)
return &node->value;
else if (node->key > key)
Search_(node->left, key);
else
Search_(node->right, key);
}
//查找,返回value
Value* Search(Key key)
{
return Search_(root, key);
}
//测试代码
int main()
{
BSTbst=BST();
bst.insert(1, 10);
bst.insert(2, 13);
bst.insert(2, 23);
bst.insert(4, 33);
//bst.insert(1, 3);
bst.insert(5, 43);
bst.insert(8, 53);
bst.insert(6, 63);
int *a = bst.Search(4);
*a = 22;
cout << *bst.Search(4) << endl;
}
二分搜索树的实现代码
#pragma once
#include
//————————————二分搜索树——————————
//查找表的实现,key 表示关键字, value 表示查找值
//因为不是完全二叉树,所以不用数组来表示,采用结构体构造节点,指针指向左右孩子的方式,将一棵树连接起来
//特性: 左孩子比节点小,右孩子比节点大
template
class BST
{
private:
struct Node {
Key key;
Value value;
Node * left;
Node * right;
Node *parent;
Node(Key key, Value value)
{
this->key = key;
this->value = value;
this->left = NULL;
this->right = NULL;
}
Node(Node* node)
{
this->key = node->key;
this->value = node->value;
this->left = node->left;
this->right = node->right;
}
};
int counts;
//以指针的方式,就可以遍历整棵树,无需像堆一样,利用数组的方式
Node *root;
//向以node为根的二叉搜索树中,插入节点(key,value)
//返回插入新节点后的二叉搜索树的根,虽然根节点的指向永远不会变,但是新的的节点得通过指针加入到二叉搜索树中,
Node* insert(Node *node, Key key, Value value)
{
if (node == NULL)
{
counts++;
//返回值需要传递地址,用new开辟空间,并将地址返回
return new Node(key, value);
}
if (key == node->key)
node->value = value;
else if (key < node->key)
{
//需要通过指针将新的节点连接到树中
Node *p = insert(node->left, key, value);
node->left = p;
}
else
{
Node *p= insert(node->right, key, value);
node->right = p;
}
return node;
}
//输入树中各个节点指针,和需要查找的key
//查看以node为根的二叉搜索树中是否包含键值为key的节点
//返回查找的键值的对应的value*
Value* Search_(Node* node,Key key)
{
if (node == NULL)
return NULL;
//如果相等,则覆盖value
if (node->key == key)
return &node->value;
else if (node->key > key)
Search_(node->left, key);
else
Search_(node->right, key);
}
//查看以node为根的二叉搜索树中是否包含键值为key的节点
//查找,返回值为0或1
bool contain_(Node* node, Key key)
{
if (node == NULL)
return 0;
if (node->key == key)
return 1;
else if (node->key > key)
contain_(node->left, key);
else //node->key < key
contain_(node->right, key);
}
Node* search(Node * node, Key key)
{
if (node == NULL)
{
return NULL;
}
if (node->key == key)
{
return node;
}
else if (node->key > key)
search(node->left, key);
else//node->keyright, key);
}
//删除
//以node为根先序遍历
void preorder(Node *node)
{
if (node != NULL)
{
cout << node->key << endl;
preorder(node->left);
preorder(node->right);
}
}
//以node为根的中序遍历
void inorder(Node *node)
{
if (node != NULL)
{
inorder(node->left);
cout << node->key << endl;
inorder(node->right);
}
}
//以node为根的后序遍历
void postorder(Node* node)
{
if (node != NULL)
{
postorder(node->left);
postorder(node->right);
cout << node->key << endl;
}
}
//销毁以node为根的二叉搜索树
void destroy(Node *node)
{
if (node != NULL)
{
destroy(node->left);
destroy(node->right);
delete node;
counts--;
}
}
//删除节点之后,树的根节点可能会发生变化,要有这个意识
//删除掉以node为根的二叉搜索树最小关键字节点
//返回删除节点后新的二分搜索树的根
Node* removeMin_key(Node * node)
{
if (node->left == NULL)
{
Node* rightnode = node->right;
counts--;
delete node;
return rightnode;
}
node->left = removeMin_key(node->left);
return node;
}
//删除节点之后,树的根节点可能会发生变化,要有这个意识
//删除掉以node为根的二叉搜索树最大关键字节点
//返回删除节点后的新的二分搜索树的根
Node* removeMax_key(Node*node)
{
if (node->right == NULL)
{
Node * rightnode = node->right;
delete node;
counts--;
return rightnode;
}
else
{
node->right = removeMax_key(node->right);
return node;
}
}
//删除节点之后,树的根节点可能会发生变化,要有这个意识
//返回删除节点之后的根节点,可以将节点从底层一个个返回上来
Node* remove_node(Node*node, Key key)
{
//搜索以node为根的二叉搜索树中key关键字,
if (node == NULL)
{
return NULL;
}
if (node->key < key)
{
node->right=remove_node(node->right, key);
return node;
}
else if (node->key > key)
{
node->left = remove_node(node->left, key);
return node;
}
else
{
if (node->left == NULL)
{
Node* rightnode = node->right;
delete node;
counts--;
return rightnode;
}
else if (node->right == NULL)
{
Node* leftnode = node->left;
delete node;
counts--;
return leftnode;
}
else //node->left != NULL&&node->right != NULL
{
//此句的下一行程序,将min_key(node->right)返回的节点删除了,所以需要重新编写构造函数,赋值之前的node
Node*successor=new Node(min_key(node->right));
//添加了,需要增加计数值
counts++;
//successor->left 是node->left 删除successor节点的根节点
successor->right = removeMin_key(node->right);
successor->left = node->left;
delete node;
//删除了,需要减少计数值
counts--;
return successor;
}
}
}
public:
BST()
{
counts = 0;
root = NULL;
}
~BST()
{
}
//返回BST的节点的数量
int size()
{
return counts;
}
//返回BST是否为空
bool isEmpty()
{
return counts ==0;
}
//查找,返回value
Value* Search(Key key)
{
return Search_(root, key);
}
//查找,返回0或1
bool contain(Key key)
{
return contain_(root, key);
}
//删除节点
void remove_node(Key key)
{
//删除关键点为key的节点
//返回删除节点之后的根节点
root = remove_node(root, key);
}
//从二叉搜索树中删除最小关键值所在的节点
void Delete_min_key()
{
if (root)
{
root=removeMin_key(root);
}
}
//从二叉搜索树中删除最大关键值所在的节点
void Delete_max_key()
{
if (root)
{
root = removeMax_key(root);
}
}
//插入
//传入查找表的key,和value
void insert(Key key ,Value value)
{
//函数的重载
root=insert(root, key, value);
}
//返回二叉索树的最小关键字的节点
Node* min_key(Node* node_)
{
//0会触发中断程序
assert(counts != 0);
Node* node = node_;
while (node->left != NULL)
{
node = node->left;
}
return node;
}
//返回二叉索树的最大关键字的节点
Node* max_key(Node* node_)
{
//0会触发中断程序
assert(counts != 0);
Node* node = node_;
while (node->right != NULL)
{
node = node->right;
}
return node;
}
//删除关键字为key节点
//返回,删除之后的二分搜索树的根
void Delete_node(Key key)
{
remove_node(root, key);
}
//——————————二叉搜索树的深度优先遍历——————————
//先序遍历
void preorder()
{
preorder(root);
}
//中序遍历
void inorder()
{
inorder(root);
}
//后序遍历
void postorder()
{
postorder(root);
}
//层序遍历
void leverorder()
{
queueq;
q.push(root);
while (!q.empty())
{
Node*node = q.front();
q.pop();
cout << node->key << endl;
if (node->left)
{
q.push(node->left);
}
if (node->right)
{
q.push(node->right);
}
}
}
}; 二分搜索树的测试代码
BSTbst=BST();
bst.insert(21, 10);
bst.insert(1, 10);
bst.insert(2, 13);
bst.insert(2, 23);
bst.insert(4, 33);
//bst.insert(1, 3);
bst.insert(34, 12);
bst.insert(5, 43);
bst.insert(8, 53);
//cout << "是否包含8:" << bst.contain(10) << endl;
bst.insert(6, 63);
//cout << bst.size() << bst.isEmpty() << endl;
//int b = 22;
//bst.Delete(8);
//cout <<"是否包含8:" <