最小生成树———prim算法和kruskal算法详解

最小生成树之prim算法（转载出处）

边赋以权值的图称为网或带权图，带权图的生成树也是带权的，生成树T各边的权值总和称为该树的权。

   最小生成树（MST）：权值最小的生成树。

   生成树和最小生成树的应用：要连通n个城市需要n－1条边线路。可以把边上的权值解释为线路的造价。则最小生成树表示使其造价最小的生成树。

   构造网的最小生成树必须解决下面两个问题：

    1、尽可能选取权值小的边，但不能构成回路；

    2、选取n－1条恰当的边以连通n个顶点；

    MST性质：假设G＝(V,E)是一个连通网，U是顶点V的一个非空子集。若(u,v)是一条具有最小权值的边，其中u∈U，v∈V－U，则必存在一棵包含边(u,v)的最小生成树。 

 

1.prim算法

  基本思想：假设G＝(V，E)是连通的，TE是G上最小生成树中边的集合。算法从U＝{u0}（u0∈V）、TE＝{}开始。重复执行下列操作：

   在所有u∈U，v∈V－U的边(u，v)∈E中找一条权值最小的边(u0,v0)并入集合TE中，同时v0并入U，直到V＝U为止。

   此时，TE中必有n-1条边，T=(V，TE)为G的最小生成树。

   Prim算法的核心:始终保持TE中的边集构成一棵生成树。

注意：prim算法适合稠密图，其时间复杂度为O(n^2)，其时间复杂度与边得数目无关，而kruskal算法的时间复杂度为O(eloge)跟边的数目有关，适合稀疏图。

看了上面一大段文字是不是感觉有点晕啊，为了更好理解我在这里举一个例子，示例如下：

 

 

 

 

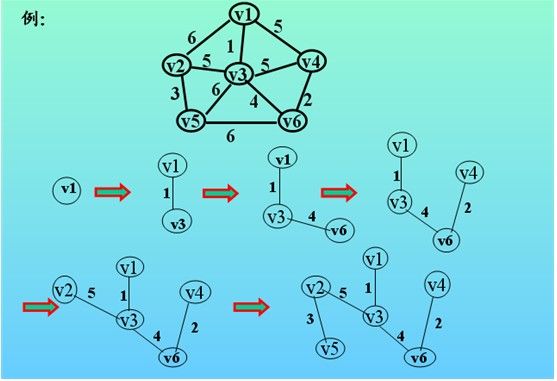
（1）图中有6个顶点v1-v6，每条边的边权值都在图上；在进行prim算法时，我先随意选择一个顶点作为起始点，当然我们一般选择v1作为起始点，好，现在我们设U集合为当前所找到最小生成树里面的顶点，TE集合为所找到的边，现在状态如下：

U={v1}； TE={}；

（2）现在查找一个顶点在U集合中，另一个顶点在V-U集合中的最小权值，如下图，在红线相交的线上找最小值。

 

 

 

 

 

通过图中我们可以看到边v1-v3的权值最小为1，那么将v3加入到U集合，（v1，v3）加入到TE，状态如下：

U={v1，v3}； TE={（v1，v3）}；

（3）继续寻找，现在状态为U={v1，v3}； TE={（v1，v3）}；在与红线相交的边上查找最小值。

我们可以找到最小的权值为（v3，v6）=4，那么我们将v6加入到U集合，并将最小边加入到TE集合，那么加入后状态如下：

U={v1，v3，v6}； TE={（v1，v3），（v3，v6）}； 如此循环一下直到找到所有顶点为止。

（4）下图像我们展示了全部的查找过程：

2.prim算法程序设计

 

（1）由于最小生成树包含每个顶点，那么顶点的选中与否就可以直接用一个数组来标记used[max_vertexes];（我们这里直接使用程序代码中的变量定义，这样也易于理解）；当选中一个数组的时候那么就标记，现在就有一个问题，怎么来选择最小权值边，注意这里最小权值边是有限制的，边的一个顶点一定在已选顶点中，另一个顶点当然就是在未选顶点集合中了。我最初的一个想法就是穷搜了，就是在一个集合中选择一个顶点，来查找到另一个集合中的最小值，这样虽然很易于理解，但是很明显效率不是很高，在严蔚敏的《数据结构》上提供了一种比较好的方法来解决：设置两个辅助数组lowcost[max_vertexes]和closeset[max_vertexes]，lowcost[max_vertexes]数组记录从U到V－U具有最小代价的边。对于每个顶点v∈V－U,closedge[v], closeset[max_vertexes]记录了该边依附的在U中的顶点。

注意：我们在考虑两个顶点无关联的时候设为一个infinity 1000000最大值。

说了这么多，感觉有点罗嗦，还是发扬原来的风格举一个例子来说明，示例如下：

过程如下表：顶点标号都比图中的小1，比如v1为0，v2为1，这里首先选择v1点。

	Lowcost[0]	Lowcost[1]	Lowcost[2]	Lowcost[3]	Lowcost[4]	Lowcost[5]	U	V-U
closeset	v1，infinity	v1，6	v1，1	v1，5	v1，infinity	v1，infinity	v1	v1,v2,v3,v4,v5,v6

从这个表格可以看到依附到v1顶点的v3的Lowcost最小为1，那么选择v3，选择了之后我们必须要更新Lowcost数组的值，因为记录从U到V－U具有最小代价的边，加入之后就会改变。这里更新Lowcost和更新closeset数组可能有点难理解，

 for (k=1;k
            if (!used[k]&&(G[j][k]
                { lowcost[k]=G[j][k];
                closeset[k]=j; }
        }
j为我们已经选出来的顶点，如果G[j][k]，则意味着最小权值边发生变化，更新该顶点的最小lowcost权值，依附的顶点肯定就是刚刚选出的顶点j，closeset[k]=j。

	Lowcost[0]	Lowcost[1]	Lowcost[2]	Lowcost[3]	Lowcost[4]	Lowcost[5]	U	V-U
closeset	v1，infinity	v1，6	v1，1	v1，5	v3，6	v3，4	v1，v3	v1,v2,v4,v5,v6

 

这样一直选择下去直到选出所有的顶点。

（2）上面把查找最小权值的边结束了，但是这里有一个问题，就是我们没有存储找到的边，如果要求你输出找到的边那么这个程序就需要改进了，我们刚开始的时候选取的是v1作为第一个选择的顶点，那我们设置一个father[]数组来记录每个节点的父节点，当然v1的父节点肯定没有，那么我们设置一个结束标志为-1，每次找到一个新的节点就将它的父节点设置为他依附的节点，这样就可以准确的记录边得存储了。

 

 

最小生成树，克鲁斯卡尔算法．（转载出处）

算法简述：

　　将每个顶点看成一个图．

　　在所有图中找权值最小的边．将这条边的两个图连成一个图，

　　重复上一步．直到只剩一个图．

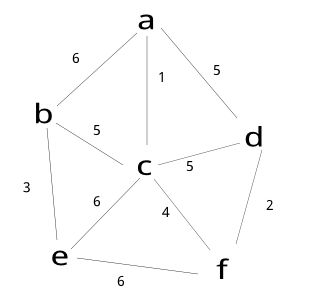
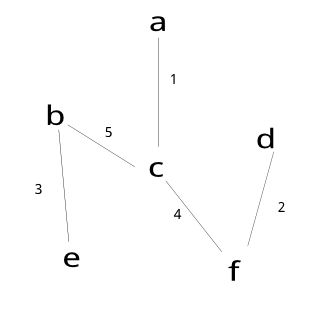
注：将ａｂｃｄｅｆ每个顶点看成一个图．将最小权值的边的两个图连接．

连接最小权值为１的两个图，这时ａ－ｃ，ｂ，ｄ，ｅ，ｆ．

连接最小权值为２的两个图，这时ａ－ｃ，ｂ，ｄ－ｆ，ｅ．

连接最小权值为３的两个图，这时ａ－ｃ，ｂ－ｅ，ｄ－ｆ．

连接最小权值为４的两个图，这时ａ－ｃ－ｆ－ｄ，ｂ－ｅ．（ｃ－ｆ）

连接最小权值为５的两个图，这时ａ－ｃ－ｂ－ｅ－ｆ－ｄ．（ｂ－ｃ）

结束．

根据上述操作，我们需要一个存储边信息的数组（Edge结构体），Edge包含了边的两个节点和权值．

1 typedef struct
2 {
3     int head;//边的始点下标
4     int tail;//边的终点下标
5     int power;//边的权值
6 } Edge;

还需要一个visited数组，用来标识图中的节点信息．

 

算法操作：

　　初始化一棵树（用来保存最小生成树，直接输出也行．）

　　将图中所有边复制到一个数组中，将数组排序（递增顺序）

　　将小边的两个顶点连接．将两个图合并成一个图．

　　重复上一步．

临街矩阵的代码实现

代码中，ｉｊｋ做循环用，ｖ１，ｖ２做边的两个顶点信息的下标，ｖｓ１，ｖｓ２做标识ｖ１和ｖ２所属图

１－２７行，初始化visited,edge,kruskal_tree等信息．

２９－４４行，生成一棵最小生成树．

３５行，ｉｆ是为了防止回路，ｖｓ１和ｖｓ２标识一个这两点是否属于一个图．

３８行，ｆｏｒ是为了将ｖｉｓｉｔｅｄ数组中ｖｓ２边成ｖｓ１，因为这时，ｖ１和ｖ２已经在一个图里了．

 

1 void kruskal(Graph * graph, Graph * kruskal_tree)
 2 {
 3     int visited[graph->vertexs];
 4     Edge edge[graph->brim];
 5     int i, j, k;
 6     int v1, v2, vs1, vs2;
 7 
 8     for ( i = 0; i < graph->vertexs; i++ )
 9         visited[i] = i;
10 
11     k = 0;
12     for ( i = 0; i < graph->vertexs; i++ )
13     {
14         for ( j = i + 1; j < graph->vertexs; j++ )
15         {
16             if ( graph->arcs[i][j] != MAX_VALUE )
17             {
18                 edge[k].head = i;
19                 edge[k].tail = j;
20                 edge[k].power = graph->arcs[i][j];
21                 k++;
22             }
23         }
24     }
25 
26     init_kruskal(graph, kruskal_tree);
27     my_sort(edge, graph->brim);
28 
29     for ( i = 0; i < graph->brim; i++ )
30     {
31         v1 = edge[i].head;
32         v2 = edge[i].tail;
33         vs1 = visited[v1];
34         vs2 = visited[v2];
35         if ( vs1  != vs2 )
36         {
37             kruskal_tree->arcs[v1][v2] = graph->arcs[v1][v2];
38             for ( j = 0; j < graph->vertexs; j++ )
39             {
40                 if ( visited[j] == vs2 )
41                     visited[j] = vs1;
42             }
43         }
44     }
45 }

 

临街矩阵源码：http://www.cnblogs.com/ITgaozy/p/5200637.html

邻接表的代码实现

１７行，ｉｆ是为了将防止边的重复输入（在邻接矩阵中，点在矩阵中是对称的，所以我们只输入一个上三角中的数据就够了．但在邻接表中，我们如何判断一条边是否已经输入过了？　我的方法是将比当前节点下标大的输入，例如右ａ，ｂ两个节点，ａ的节点小与ｂ，我们在输入ｂ的信息时，由于ａ的节点下标比ｂ小，不输入ａ－ｂ这条边，因为我们在输入ａ的信息时，ａ－ｂ这条边已经输入过了．

 

 1 void kruskal(Graph * graph, Graph * kruskal_tree)
 2 {
 3     int visited[graph->vertexs];
 4     int i, j;
 5     Edge edge[graph->brim];
 6     int v1, v2, vs1, vs2;
 7     Arc_node * cur, * tmp;
 8 
 9     for ( i = 0; i < graph->vertexs; i++ )
10         visited[i] = i;
11 
12     for ( i = 0, j = 0; i < graph->vertexs; i++ )
13     {
14         cur = graph->adjlist[i].next;
15         while ( cur != NULL )
16         {
17             if ( cur->pos > i )
18             {
19                 edge[j].head = i;
20                 edge[j].tail = cur->pos;
21                 edge[j].power = cur->distance;
22                 j++;
23             }
24             cur = cur->next;
25         }
26     }
27 
28     init_kruskal(graph, kruskal_tree);
29     my_sort(edge, graph->brim);
30 
31     for ( i = 0; i < graph->brim; i += 1 )
32     {
33         v1 = edge[i].head;
34         v2 = edge[i].tail;
35         vs1 = visited[v1];
36         vs2 = visited[v2];
37         if ( vs1 != vs2 )
38         {
39             if ( kruskal_tree->adjlist[v1].next == NULL )
40             {
41                 kruskal_tree->adjlist[v1].next = make_node(v2, edge[i].power);
42             }
43             else
44             {
45                 tmp = kruskal_tree->adjlist[v1].next;
46                 while ( tmp->next != NULL )
47                     tmp = tmp->next;
48                 tmp->next = make_node(v2, edge[i].power);
49             }
50             for ( j = 0; j < graph->vertexs; j++ )
51             {
52                 if ( visited[j] == vs2 )
53                     visited[j] = vs1;
54             }
55         }
56     }
57 }

 

 邻接表源码：http://www.cnblogs.com/ITgaozy/p/5200643.html