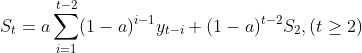指数平滑预测--单指数模型
前言:2018年华为软赛初赛已经结束,很高兴我们团队取得西北赛区36强的成绩。最近我会在博客上介绍我们使用过的预测方法,首先是指数平滑模型,指数平滑模型是简单高效的预测模型(分数高),我们主要使用的二次指数平滑和三次指数平滑,按7天进行数据加和,来预测短期数据。
时间序列预测方法的基本思想是:预测一个现象的未来变化时,用该现象的过去行为来预测未来。即通过时间序列的历史数据揭示现象随时间变化的规律,将这种规律延伸到未来,从而对该现象的未来作出预测。它的重要分支指数平滑法是由早期的移动平均法发展而来的。
指数平滑预测法是一种确定性的平滑预测法。其实质是:通过计算指数平滑平均数来平滑时间序列,消除历史统计序列中的随机波动,以找出其主要发展趋势。根据设置参数的不同可以分为单指数预测、双指数预测和三指数预测。其中,单指数具有一个参数,适合于具有平稳性特征时间序列的预测,也称为平稳性预测。双指数预测具有两个参数,适合于具有趋势性特征时间序列的预测,也称为趋势性预测。三指数预测具有三个参数,适合于具有趋势和季节性或周期性特征时间序列的预测,也称为季节性或周期性预测。指数平滑的三种预测方法中,预测曲线拟合程度的好坏与预测结果的准确度有关,而预测曲线的拟合程度与设定的参数值有直接关系。所以,参数的好坏非常重要。
指数平滑是当前产生平滑时间序列的一种比较流行的方法,也是画拟合曲线的一种方法,同时还可以对未来进行预测。指数平滑预测方法的基本思想是在预测下一周期的指标的同时,既考虑这个周期的指标,又不忘记前面的指标。在移动平均方法中,对每个数据赋予相同的权重,而指数平滑可以根据参数对数据赋予不同的权重,这样就可以获得更好的拟合曲线和预测结果。
单指数模型
单指数平滑具有一个平滑参数,适合对具有平稳特性的时间序列数据进行拟合和预测,其中数据的平稳特性是指数据的变化波动不大。
(1)平滑公式
用![]() 表示实际点的数据值,
表示实际点的数据值,![]() 表示平滑点的数据值,对于序列中任一时刻点t,平滑值
表示平滑点的数据值,对于序列中任一时刻点t,平滑值![]() 的平滑计算公式如式(1-1)所示:
的平滑计算公式如式(1-1)所示:
![]() (1-1)
(1-1)
(2)初始化
单指数平滑的起始平滑点是![]() ,一般有两种方法进行初始化
,一般有两种方法进行初始化![]() 。一种方法是
。一种方法是![]() ,另一种方法是取实际点的前四个或者前五个的平均值。
,另一种方法是取实际点的前四个或者前五个的平均值。
(3)预测公式
t+1序列时刻单指数平滑公式如式(1-2)所示:
![]() (1-2)
(1-2)
t+i序列时刻单指数平滑公式如式(1-3)所示:
![]() (1-3)
(1-3)
式中i表示是经过的时刻点,也表示超前预测时刻。
下面对平滑公式进行扩展,用基本的平滑公式代替![]() ,如式(1-4)所示:
,如式(1-4)所示:
![]() (1-4)
(1-4)
然后,接着替代![]() ,
,![]() ,如此递归,直到
,如此递归,直到![]() ,这样就可以得到式(1-5),如下所示:
,这样就可以得到式(1-5),如下所示:
比如,当t=5时,如式(1-6)所示:
![]() (1-6)
(1-6)
权重![]() 呈几何递减,所以较早数据的权重较小,所起的作用也就越小,这也是为什么将指数平滑方法称为指数平滑的原因所在。
呈几何递减,所以较早数据的权重较小,所起的作用也就越小,这也是为什么将指数平滑方法称为指数平滑的原因所在。
(4)二次指数平滑模型
在一次指数平滑预测公式中,无论是一步预测还是多步预测都使用同一公式,这对没有趋势的稳定序列是可行的。但是,若是用在上升或是下降趋势明显的需求序列上就不够理想。二次指数平滑就是为弥补这种缺陷而设计的一种方法,但它不是直接用于序列预测的方法,而是为计算有线性趋势的线性预测方程的系数服务的。
所谓二次指数的平滑方法,是对一次指数平滑后的序列数据再作一次指数平滑,其平滑公式如下式(2-1)所示:
式中,![]() 是二次指数平均值,
是二次指数平均值,![]() 为平滑常数。
为平滑常数。
同一次指数平滑公式一样,在使用二次指数平滑公式时,也涉及初始值![]() 的取法。但随着时间的推移,初始值的影响是很小的。其取法与一次指数平滑的取法相似。
的取法。但随着时间的推移,初始值的影响是很小的。其取法与一次指数平滑的取法相似。
由于时间序列具有线性趋势,故设线性预测方程如式(2-2)所示:
![]() (2-2)
(2-2)
式中![]() 称为预测时效,由指数平滑方法的基本定理有下式:
称为预测时效,由指数平滑方法的基本定理有下式:
由此得到预测公式如式所示:
数值实验证明,用二次指数平滑公式进行预测时,除序列的转折点外,其它点的预测精度都比一次指数平滑的预测精度高。此外,使用二次指数平滑进行预测会产生滞后误差的问题。
//二次指数平滑
int ExponentialSmoothing(double x[], int len, int pre_time)
{
double weight = 0.912;
double at = 0.0;
double bt = 0.0;
double* onetime_pre = (double *)malloc(len * sizeof(double));
double* twotime_pre = (double *)malloc(len * sizeof(double));
double *y=(double *)malloc(pre_time*sizeof(double));
memset(onetime_pre, 0, len * sizeof(double));
memset(twotime_pre, 0, len * sizeof(double));
memset(y,0,pre_time*sizeof(double));
//一次指数平滑
onetime_pre[0] = x[0]; //init
for (int i = 1; i < len; i++)
{
onetime_pre[i] = weight * x[i] + (1 - weight) * onetime_pre[i - 1];
}
//二次指数平滑
twotime_pre[0] = (onetime_pre[0] + onetime_pre[1] + onetime_pre[2]) / 3; //init
for (int i = 1; i < len; i++)
{
twotime_pre[i] = weight * onetime_pre[i] + (1 - weight) * twotime_pre[i - 1];
}
//计算截距和斜率
at = 2 * onetime_pre[len -1] - twotime_pre[len - 1];
bt = weight / (1 - weight) * (onetime_pre[len - 1] - twotime_pre[len - 1]);
//printf("at = %f\n", at);
//printf("bt = %f\n", bt);
for (int T = 0; T < pre_time; T++)
{
y[T] = at + bt * (T + 1);
}
double result=sumAllVectord(y,pre_time);
if(result<0) result=0;
free(onetime_pre);
free(twotime_pre);
free(y);
return floor(result);
} (5)三次指数平滑模型
当观察值分布出现曲率时,一般情况下二次指数平滑不再适用,要用三次指数平滑法,即非线性预测模型。三次指数平滑是将二次指数平滑值再进行一次系数平滑,如式(3-1)所示:
![]() (3-1)
(3-1)
三次指数平滑非线性模型预测公式如式(3-2)所示:
![]() (3-2)
(3-2)
系数为:
(3-3)
在历史数据出现曲率时,三次指数平滑模型预测值较二次指数平滑模型更加准确。
int ExponentialSmoothing(double x[], int len, int pre_time){
double weight = 0.6;
double at = 0.0;
double bt = 0.0;
double ct = 0.0;
double* onetime_pre = (double *)malloc(len * sizeof(double));
double* twotime_pre = (double *)malloc(len * sizeof(double));
double* threetime_pre = (double *)malloc(len * sizeof(double));
double *y=(double *)malloc(pre_time*sizeof(double));
memset(onetime_pre, 0, len * sizeof(double));
memset(twotime_pre, 0, len * sizeof(double));
memset(threetime_pre, 0, len * sizeof(double));
memset(y,0,pre_time*sizeof(double));
//一次指数平滑
onetime_pre[0] = x[0]; //init
for (int i = 1; i < len; i++)
{
onetime_pre[i] = weight * x[i] + (1 - weight) * onetime_pre[i - 1];
}
//二次指数平滑
twotime_pre[0] = (onetime_pre[0] + onetime_pre[1] + onetime_pre[2]) / 3; //init
for (int i = 1; i < len; i++)
{
twotime_pre[i] = weight * onetime_pre[i] + (1 - weight) * twotime_pre[i - 1];
}
//三次指数平滑
threetime_pre[0] = (twotime_pre[0] + twotime_pre[1] + twotime_pre[2]) / 3; //init
for (int i = 1; i < len; i++)
{
threetime_pre[i] = weight * twotime_pre[i] + (1 - weight) * threetime_pre[i - 1];
}
//计算截距和斜率
at = 3 * onetime_pre[len -1] - 3 * twotime_pre[len - 1] + threetime_pre[len - 1];
bt = weight / (2 * (1 - weight) * (1 - weight)) * ((6 - 5 * weight) * onetime_pre[len - 1] - 2 * (5 - 4 * weight) * twotime_pre[len - 1] + (4 - 3 * weight) * threetime_pre[len - 1]);
ct = (weight * weight) / (2 * (1 - weight) *(1 - weight)) * (onetime_pre[len - 1] - 2 * twotime_pre[len - 1] + threetime_pre[len - 1]);
//printf("at = %f\n", at);
//printf("bt = %f\n", bt);
for (int T = 0; T < pre_time; T++)
{
y[T] = at + bt * (T + 1) + ct * (T + 1) * (T + 1);
}
double result=sumAllVectord(y,pre_time);
if(result<0) result=0;
free(onetime_pre);
free(twotime_pre);
free(threetime_pre);
free(y);
return floor(result);
}