最近算法课上完成了一道作业题,Vertex Cover,拿出来与大家分享一下。算法不能说有多好,有问题欢迎致信[email protected]
1,问题描述
首先Vertex Cover问题是NP完全问题,所以写的代码仅仅针对该问题的小规模情况。大规模情况下可能就需要使用近似算法。在算法导论的34章NP完全性的34.5.2节就给出了近似解法。当然,这道作业题是要求求出准确的解,所以就不考虑近似算法了。
先介绍一下这个问题。Vertex Cover问题指的是给定一个N个点,M条边的无向图G(点的编号从1至N),问是否存在一个不超过K个点的集合S,使得G中的每条边都至少有一个点在集合S中。
解释这个问题,N个点,M条边的无向图,每次去掉一个点以及该点相邻的边,直到把所有的边都去掉。一个可能的过程如下,红色为待去除的点:
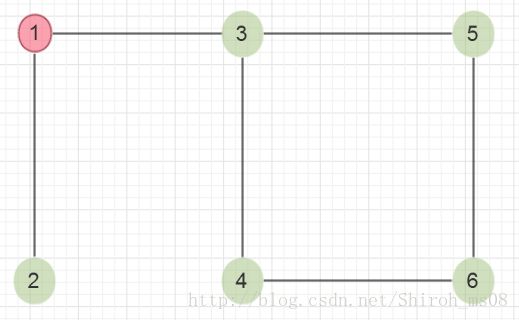
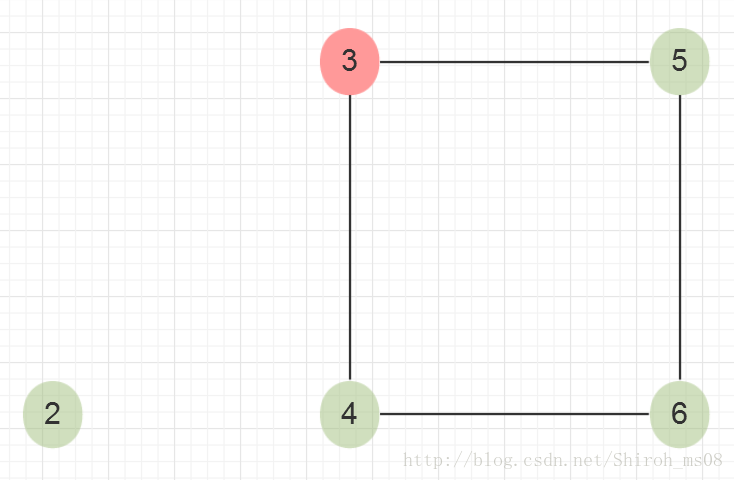


问题的目的就是在所有可能的情况中,找出一种使用的点最少的情况(可能并不唯一,只要求出一个即可)。
2,思路
首先每次找到当前情况下度数最大的点来删除未必能够得到最优解,反例如下图,如果开始就去掉度最多的最中间的点,那么就得不到最优解了:
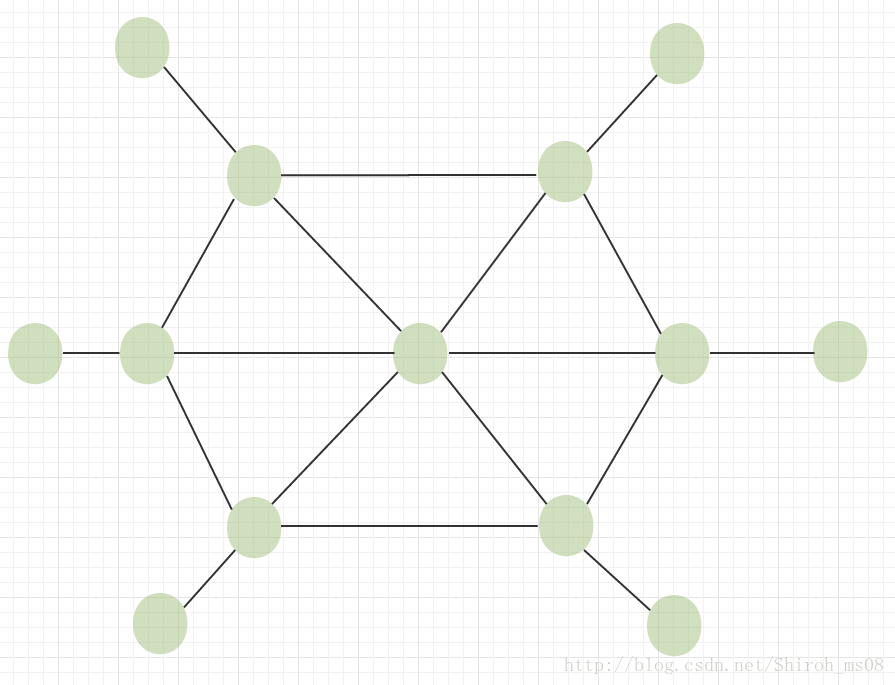
但是每次都尝试当前度最高的点在很多情况下的确能够帮助尽快找到最优解。
其次,如果按照对于某个点选择,不选择情况分别进行处理,则算法需要耗费大量的时间,最坏时候要尝试近2^n种情况。所以必须有一定的准则进行剪枝。
综上,处理的思路主要有两个方面,一个方面是选择优先局部最优的点进行处理,以期望尽早找到最优的一个情况;另一个方面是设计一定的准则,去除掉一些不可能产生更优解的情况,或者是把一些必然会发生的情况直接进行确认都不用进行探寻。
3,准则
为了减少要遍历的情况的数目,按照一定的准则1,去除不可能产生更优解的情况;2,一些必然发生的情况直接加入当前解。
1)去除不可能产生更优解的情况
如果当前已经探索过的结点数仅仅比当前最优解少一个,那么就不用继续探索了,因为最好也只能找到和当前最优解一样优的解。
如果当前最大的结点的度,加上(当前第二大结点的度*(当前最优解-当前已探索过的结点-2))仍然小于未消除过的边的数目,那么就不用继续探索了,因为不可能得到更优解了。
2)必然发生的情况直接加入当前解
如果当前的结点中存在度为1的结点,该度为1的结点(设为A)所在边的另一个结点(设为B)必然会存在于当前解中,因为无论B的度是否为1,那么要消除这条边则A,B两个结点任意选一个就可以消除,选B符合情况。而且B还有可能度大于1,也就是如果A可以存在于当前解中,则B替代A得到的解只会和A一样优或者更优。
如果不选择某个结点,那么该结点相邻的点都必须加入当前解中,否则会存边无法被消除。
4,代码
所以得到的代码如下:
#include
#include
因为过程中很多是查询,所以数据结构上使用了map来存储边和结点的信息.其实其中有很多地方可以精简。




