【深度学习系列】——梯度下降算法的可视化解释(动量,AdaGrad,RMSProp,Adam)!
这是深度学习系列的第二篇文章,欢迎关注原创公众号 【计算机视觉联盟】,第一时间阅读我的原创!回复 【西瓜书手推笔记】 还可获取我的机器学习纯手推笔记!
直达笔记地址:机器学习手推笔记(GitHub地址)
深度学习系列
【深度学习系列】——深度学习简介
笔记预览
在这篇文章中,由于有大量的资源可以解释梯度下降,因此,我想在视觉上引导您了解每种方法的工作原理。借助我构建的梯度下降可视化工具,希望我可以为您提供一些独特的见解,或者至少提供许多GIF。
这里的重点是比较和对比这些方法。
Vanilla Gradient Descent
在机器学习的上下文中,梯度下降的目标通常是使机器学习问题的损失函数最小化。一个好的算法可以快速,可靠地找到最小值(即,它不会卡在局部最小值,鞍点或平稳区域中,而是求出全局最小值)。
基本的梯度下降算法遵循这样的思想,即梯度的相反方向指向下部区域的位置。因此,它会沿梯度的相反方向迭代。对于每个参数theta,它执行以下操作:

Theta是您要优化的一些参数(例如,神经网络中神经元到神经元连接的权重,线性回归中特征的系数等)。机器学习优化设置中可能有成千上万个这样的theta。Delta是算法每次迭代后theta的变化量;希望随着每个这样的变化,θ逐渐接近最佳值。
由于人类的感知仅限于3维,在我所有的可视化中,假设我们只有两个参数(或theta)需要优化,它们由图中的x和y维表示。表面是损失函数。我们想要找到在曲面最低点的(x,y)组合。这个问题对我们来说微不足道,因为我们可以看到整个表面。但是球却看不到;它一次只能迈出一步,并探索周围的环境,就像只用手电筒在黑暗中行走一样。
Momentum
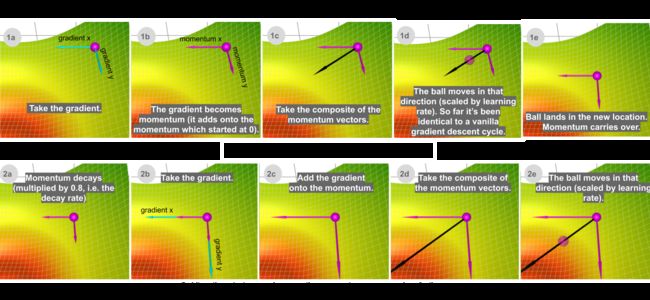
动量算法(或简称为动量)的梯度下降借鉴了物理学的思想。想象一下,将球滚动到无摩擦碗内。累积的动量并没有停止在底部,而是将其向前推动,并且球不断来回滚动。
我们可以将动量的概念应用于我们的Vanilla Gradient Descent算法。在每个步骤中,除了规则的渐变以外,它还增加了上一步的运动。在数学上,它通常表示为:
如果我稍微改动一下这个等式,并记录“梯度的(衰减的)累积和”,会更直观。当我们稍后介绍Adam算法时,这也会使事情变得更简单。
让我们考虑两种极端情况,以便更好地了解此衰减率参数。如果衰减率为0,则它与Vanilla Gradient Descent梯度下降完全相同。如果衰减率为1,则它会像我们在开头提到的无摩擦碗类推一样不断地来回摇摆;你不希望出现这种情况。通常,衰减率大约在0.8-0.9之间选择-就像一个带有一点摩擦的表面,因此它最终会减速并停止。
那么,动量在哪些方面比Vanilla Gradient Descent更好?在下图的比较中,您可以看到两个优点:
- 动量只是移动得更快(因为它累积了所有动量)
- 动量有逃避局部最小值的作用(因为动量可能将其推离局部最小值)。同样,正如我们稍后将看到的那样,它还将更好地通过高原地区。
AdaGrad
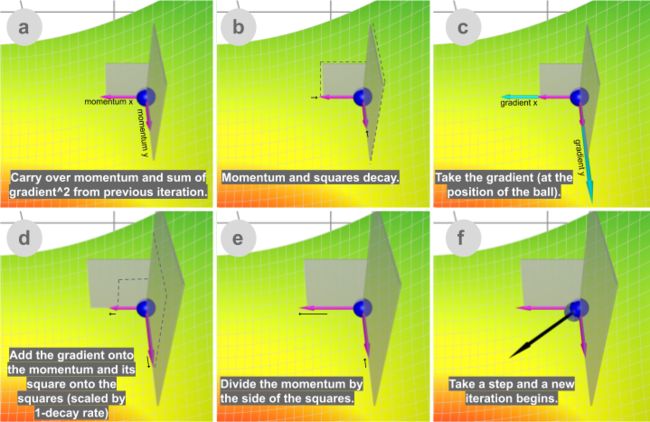
Ada自适应梯度定向算法(简称AdaGrad)不是跟踪动量之类的梯度总和,而是跟踪梯度平方的总和,并使用它来适应不同方向的梯度。方程通常用张量表示。在这里,我将避免张量来简化语言。对于每个维度:
在ML优化中,某些功能非常稀疏。稀疏特征的平均梯度通常很小,因此以慢得多的速度训练这些特征。解决此问题的一种方法是为每个功能设置不同的学习率,但这会很快变得混乱。
AdaGrad使用这种想法解决了这个问题:您更新的功能越多,将来更新的功能就越少,从而为其他功能(例如稀疏功能)提供了赶超的机会。用视觉术语来说,您更新了此功能有多少表示您在此维度中已移动了多少,并且此概念是由梯度平方的累积和所捕获的。注意,在上面的逐步网格图示中,如果没有重新调整缩放比例(1b),球将大部分垂直向下移动;通过调整(1d),它会沿对角线移动。
此属性使AdaGrad(以及其他类似的基于梯度平方的方法,如RMSProp和Adam)可以更好地逃避鞍点。AdaGrad将采取直线路径,而梯度下降(或与此相关的,动量)采取的办法“让我先滑下陡坡也许担心慢方向后”。有时,香草梯度下降可能会在两个方向的梯度均为0且在此处完全满足的鞍点处停止。
RMSProp
AdaGrad的问题在于它的运行速度非常慢。这是因为梯度平方的总和只会增加而不会缩小。RMSProp加入衰减因子修复该问题。
更精确地,梯度平方的和实际上是梯度平方的衰减的和。衰减率仅表示最近的梯度²很重要,而很久以前的梯度基本上已被忘记。附带说明一下,术语“衰减率”有点用词不当。与我们在动量中看到的衰减率不同,除衰减外,此处的衰减率还具有缩放效果:它将整个项按比例缩小(1-delay_rate)。换句话说,如果将delay_rate设置为0.99,则除了衰减外,梯度平方的总和将为AdaGrad的sqrt(1- 0.99)= 0.1,因此对于相同的步骤,该步长约为10倍。学习率。
为了了解衰减的影响,在这种直接对比中,AdaGrad white(白色)最初与RMSProp(绿色)保持一致,这与调整后的学习速率和衰减速率一样。但是AdaGrad的平方平方和累积起来如此之快,以至于很快就变得庞大起来(由动画中的平方大小证明)。他们付出了沉重的代价,最终AdaGrad实际上停止了前进。另一方面,由于衰减率,RMSProp始终将正方形保持在可管理的大小范围内。这使得RMSProp比AdaGrad更快。
Adam
最后但并非最不重要的,Adam(Adaptive Moment Estimation的简称)开出最好的动量和RMSProp的两全其美。Adam在经验上表现良好,因此近年来,它通常是深度学习问题的首选。
让我们看一下它是如何工作的:
Beta1是第一时刻的衰减率,即梯度(又称为动量)之和,通常设置为0.9。Beta 2是第二个时刻的衰减率,是梯度平方的总和,通常设置为0.999。
总结
总之,梯度下降是一类算法,旨在通过遵循梯度来找到函数上的最小点。Vanilla Gradient Descent正好遵循梯度(由学习率定标)。改善梯度下降的两个常用工具是梯度的总和(第一力矩)和梯度平方的总和(第二动量)。动量法使用具有衰减率的一阶矩来获得速度。AdaGrad使用无衰减的二阶矩来处理稀疏特征。RMSProp使用第二时刻通过一个衰减率来从AdaGrad加速。Adam同时使用第一刻和第二刻,通常是最佳选择。
Reference
http://www.cs.toronto.edu/~tijmen/csc321/slides/lecture_slides_lec6.pdf
https://ruder.io/optimizing-gradient-descent/index.html#adagrad
https://bl.ocks.org/EmilienDupont/aaf429be5705b219aaaf8d691e27ca87
原文链接:https://towardsdatascience.com/a-visual-explanation-of-gradient-descent-methods-momentum-adagrad-rmsprop-adam-f898b102325c
思考
你平时都使用什么优化算法呢?欢迎留言区说出你的观点!
有收获吗?来个关注和点赞吧,让更多的人看到这篇文章
- 点赞,让更多的人看到这篇文章
- 文章首发原创公众号 【计算机视觉联盟】,第一时间阅读文章,回复 【西瓜书手推笔记】 获取PDF下载!
- 欢迎关注我的博客,我们一起学习进步!